Journal of Flow Control, Measurement & Visualization
Vol.04 No.04(2016), Article ID:71113,19 pages
10.4236/jfcmv.2016.44013
On Switching of a Flip-Flop Jet Nozzle with Double Ports by Single-Port Control
Tatsuya Inoue, Fumiaki Nagahata, Katsuya Hirata
Department of Mechanical Engineering, Doshisha University, Kyoto, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 17, 2016; Accepted: August 17, 2016; Published: October 10, 2016
ABSTRACT
This research deals with the oscillation mechanism of a flip-flop jet nozzle with a connecting tube, based on the measurements of pressures and velocities in the connecting tube and inside the nozzle. The measurements are carried out varying: 1) the inside diameter d of the connecting tube; 2) the length L of the connecting tube and 3) the jet velocity VPN from a primary-nozzle exit. We assume that the jet switches when a time integral reaches a certain value. At first, as the time integral, we introduce the accumulated flow work of pressure, namely, the time integral of mass flux through a connecting tube into the jet-reattaching wall from the opposite jet-un-re- attaching wall. Under the assumption, the trace of pressure difference between both the ends of the connecting tube is simply modeled on the basis of measurements, and the flow velocity in the connecting tube is computed as incompressible flow. Second, in order to discuss the physics of the accumulated flow work further, we conduct another experiment in single-port control where the inflow from the control port on the jet-reattaching wall is forcibly controlled and the other control port on the opposite jet-un-reattaching wall is sealed, instead of the experiment in regular jet’s oscillation using the ordinary nozzle with two control ports in connection. As a result, it is found that the accumulated flow work is adequate to determine the dominant jet- oscillation frequency. In the experiment in single-port control, the accumulated flow work of the inflow until the jet’s switching well agrees with that in regular jet’s oscillation using the ordinary nozzle.
Keywords:
Flip-Flop Jet Nozzle, Flowmeter, Fluidics, Mixing, Flow Control

1. Introduction
The flip-flop jet nozzle (hereinafter, referred to as FFJN) is regarded as one kind of fluidic oscillator, which is oscillating devices among the fluidics. The fluidics, or the elements in fluid logic, is applications of the Coanda effect where a jet reattaches to a solid side wall, and has been researched since the 1960s [1] - [5] . The FFJN retains useful features as well as other flow-induced-vibration devices: namely, 1) low production cost and high reliability due to non-mechanically-moving parts; 2) usability due to a linear frequency response in proportion to flow rate; and 3) robustness against fluid density, temperature, pressure and composition. Owing to the above features, the FFJN is applicable for such products as flow meters, fuel injectors, micro mixers and various control devices to disturb the shear layer or to enhance heat transfer, not only for single- phase flows but also for multi-phase flows. Thus, the FFJN is often called a “fluidic oscillator” or “oscillatory-jet-type flowmeter” in different applications.
In such a context, there have been many researches on the FFJN in both fundamental and practical approaches [6] - [22] . Besides, various simplified FFJN’s without control ports, chambers, feedback loop (or connecting tube) and so on, have been reported [23] - [30] .
Among them, in order to reveal the flow inside the FFJN, we have carried out the measurements of unsteady flow-velocity distributions by an ultrasound-velocity-profile (UVP) monitor which gives us instantaneous information with higher accuracy in comparison to the conventional particle-image velocimetry [19] . Because the flow inside the FFJN is usually turbulent with random perturbations in addition to a dominant jet’s oscillation, we conducted conditional sampling by the phase-averaging technique using the flow velocity in the connecting tube as a reference signal. However, the oscillation mechanism of the FFJN has not been fully understood yet. In general, it is still difficult to predict the jet-oscillation frequency, which depends upon such various parameters as connecting-tube length, connecting-tube volume, flow rate, nozzle’s geometries and so on according to Raman et al. [12] , even in the present state.
Our purpose is to elucidate the oscillation mechanism of the FFJN. In the present study, we focus upon a dominant jet-oscillation frequency of the FFJN, based on the measurements of pressures and velocities in the connecting tube and inside the FFJN, and attempt to find out the universal number which determines the jet-oscillation frequency. The measurements are carried out, varying: 1) the inside diameter d of the connecting tube; 2) the length L of the connecting tube and 3) the jet velocity VPN from a primary-nozzle exit. We assume that the jet switches when a time integral reaches a certain value. At first, as this time integral which can be the universal number for the jet’s switching, we introduce the accumulated flow work of pressure, namely, the time integral of mass flux through a connecting tube into the jet-reattaching wall from the opposite jet-un-reattaching wall. Under the assumption, the trace of pressure difference between both the ends of the connecting tube is simply modeled on the basis of measurements. Such modeling is the same as Funaki et al. [31] . Using this model, the flow velocity in the connecting tube is computed by the Runge-Kutta method as incompressible flow. Second, in order to discuss the physics of the accumulated flow work further, we conduct another experiment in single-port control where the inflow from one control port on the jet-reattaching wall is forcibly controlled by a blower-and-value system and the other control port on the opposite jet-un-reattaching wall is sealed by a plug, as opposed to the experiment in regular oscillation using the ordinary FFJN with two control ports in connection.
More specifically, in our previous study Funaki et al. [31] , the accumulated flow work was investigated, namely the time integral of momentum flux. However, there is a possibility of predicting the jet-oscillation frequency more directly. So, we attempt to examine two kinds of integrals; namely, the time integral of momentum flux, and the time integral of mass flux.
To predict the dominant frequency is very useful and strongly needed in many practical aspects, as we have not yet established any general prediction methods as mentioned above. One of the main factors preventing the establishment is the spatial-and- temporal complexity of the flow inside the FFJN: for example, quasi-steady approaches are not suitable even for very-low dominant frequencies and the momentum-theory approaches are difficult in setting the control volume. Therefore, the present approach could be effective for a breakthrough, in addition to our previous study Funaki et al. [31] .
2. Experimental Method
2.1. Model: FFJN
Figure 1 shows the present model of a FFJN, together with its main dimensions. The FFJN consists of a primary nozzle, two side walls, two control ports, two chambers and a connecting tube. The two chambers with the control ports on the side walls are linked to each other by the connecting tube, to cause regular jet oscillation. The basic dimensions of the FFJN are determined according to Viets [8] . In addition to the experiment in regular jet’s oscillation using the ordinary FFJN with two control ports in connection, we conduct another experiment in single-port-control where we seal one control port by a plug and forcibly feed fluid from the other un-sealed control port.
Figure 1. Model: a flip-flop jet nozzle (FFJN).
Table 1 summarises the present experimental parameters. The chief geometric and kinetic parameters are as follows. In a characteristic length scale the spacing s of the primary-nozzle throat and the nozzle span S are fixed to 0.01 m and 0.05 m, respectively. So, the corresponding aspect ratio A (º S/s) is equal to 5. The control port with a breadth b is on each side wall, where b is fixed to the same as s in the present study. The gap between the side walls and the streamwise length of the side walls are denoted by GSW and LSW, respectively. Their reduced forms GSW/s and LSW/s are fixed to 2 and 4.5, respectively. A sole kinetic parameter, the Reynolds number Re, is defined by ρVPN s/μ, where ρ, VPN and μ denote the density of fluid, the mean velocity at a primary-nozzle exit and the viscosity of fluid, respectively. In the regular-oscillation experiment, the connecting tube with a length L has a circular cross section with an inside diameter d. Their reduced forms d/s and L/s vary from 1.2 to 1.4 and from 100 to 300, respectively. On the other hand, in the single-port-control experiment, a flow-increment rate coefficient K (see later for its definition) varies from 1 × 10−4 to 3.5 × 10−4 according to the results in the regular oscillation experiment.
Table 1. Experimental parameters.
2.2. Experimental Apparatus for Regular Oscillation
Figure 2 shows the schematic diagram of the present experimental apparatus in a regular-oscillation experiment. The main part of an ordinary FFJN with a primary nozzle (No. 6 in Figure 2), two control ports, two chambers (Nos. 11 & 12) and the connecting tube (No. 5) consists of acrylic-resin plates and a PVC tube. The working fluid is air, which is provided by an air compressor (No. 1) into the primary nozzle (No. 6) of the FFJN, through an air dryer (No. 2), a pressure regulator (No. 3), a flow meter (No. 4) and a long straight duct. The rectification duct in the upstream of the primary nozzle is straight and enough long (200 s = 2 m) to suppress the pulsation included in primary-nozzle jet. Volumetric flow rate into the FFJN measured by the flow meter is compensated using both the temperature and the pressure detected by a thermocouple and a pressure transducer which are placed adjacent to the flow meter. Pressures and velocities at several points are simultaneously measured by four pressure transducers KYOWA PGM-G (Nos. 7 - 10), and two hot-wire anemometers KANOMAX 7000 with I-type probes (Nos. 13 & 14), respectively. More specifically, two (Nos. 7 & 8) of the four pressure transducers are near the connecting-tube ends, one (No. 9) of the four is in the upstream of the primary nozzle, and the other (No. 10) of the four is on the side- wall inside the FFJN. One of the two hot-wire anemometers (No. 13) is for the measurement of the flow velocity inside the connecting-tube, and the other one (No. 14) is for the measurement of the flow velocity just outside the FFJN exit. The hot-wire anemometers are calibrated using a Pitot tube outside the experimental apparatus for each measurement whose duration is less than 2 hours. These signals are recorded and analyzed by a spectrum analyzer (No. 17) and a personal computer (No. 18).
2.3. Experimental Apparatus for Single-Port Control
Figure 3 shows the schematic diagram of the present apparatus in the single-port experiment. The FFJN has a single control port instead of dual control ports, as in the regular
Figure 2. Experimental apparatus for regular oscillation in ordinary FFJN operation.
Figure 3. Experimental apparatus for single-port control.
oscillation experiment. The control port on the opposite side is sealed by a plug, being flush with a side wall. As well as the regular-oscillation experiment, the working fluid is air, which is provided by an air compressor (No. 10 in the figure) into a primary nozzle (No. 20) of the FFJN, through an air dryer (No. 11), a pressure regulator (No. 3), a flow meter and a long straight duct. Volumetric flow rate into the FFJN measured by the flow meter is compensated using both the temperature and the pressure detected by a thermocouple and a pressure transducer which are placed adjacent to the flow meter. The inflow from the control port is driven by a blower through a tube (No. 1), which is regulated by a flow-control value (No. 4). In the single-port-control experiment, the jet from the primary nozzle is reattached to the side wall with the control port in advance. Then, we force the jet to switch by the inflow, from the side wall to the opposite side wall without the control port. Pressures and velocities at several points are simultaneously measured by two pressure transducers (Nos. 15 & 16) and two hot-wire anemometers (Nos. 17 & 18), respectively. These signals are recorded and analysed by a personal computer (No. 7).
In the single-port-control experiment, we quantitatively characterise the magnitude of the inflow using volumetric flow rate QT from the control port through the tube, which is detected by a hot-wire anemometer at the tube end adjacent to a chamber and the control port. So, prior to the single-port-control experiment, we need the calibration between QT and hot-wire anemometer signal VT. Figure 4 shows the schematic diagram of the apparatus for the calibration. The working fluid is air, which is provided by a blower (No. 1 in the figure) through a tube with a diameter d into a U-tube with wider cross section than the tube. Pressure and velocity at the tube end are simultaneously measured by a pressure transducer (No. 13) and a hot-wire anemometer (No. 14), respectively. The actual value of volumetric flow rate QT is detected by a measuring bar (No. 6) attached to a float on the anterior water surface of the U-tube. We record the value of the measuring bar by a camcorder (No. 5). These signals are recorded and analysed by a personal computer (No. 9). Figure 5 shows the result of the calibration, where the time history of the flow rate QT based on the flow velocity VT is measured by
Figure 4. Experimental apparatus for the calibration of volumetric flow rate QT.
Figure 5. Flow rate QT based on VT measured by a hot-wire anemometer, together with that by a camcorder.
the hot-wire anemometer, together with the actual QT by the hot-wire anemometer measured by a camcorder. We compensate QT on the basis of this result, then determine QT in the single-port-control experiment.
3. Results and Discussion
3.1. Regular Oscillation: Jet-Oscillation Frequency and Connecting-Tube Flow
The frequency f of jet’s oscillation is important not only from an academic viewpoint but also from a industrial viewpoint. According to Raman et al. [12] , f depends upon such various parameters as connecting-tube length, connecting-tube volume, flow rate, nozzle’s geometries and so on. However, it is still difficult to predict f even in the present stage. So, we first propose an empirical formula to determine f. In the present study, we get the experimental value f by the Fourier analysis on the flow-velocity fluctuation detected at the FFJN exit (No. 14 in Figure 2). As governing parameters for f, we suppose three geometric ones in addition to mean velocity VPN at a primary-nozzle exit, fluid density ρ and fluid viscosity μ. The three geometric parameters are the spacing s of a primary-nozzle throat, the length L of a connecting tube and the inner diameter d of a connecting tube. We regard s, VPN and ρ as characteristic scales. Then, according to the dimensional analysis, we get
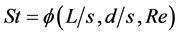 , (1)
, (1)
where 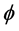 denotes an arbitrary function. In this Equation (1), we consider a normalised f, namely, the Strouhal number St, instead of f. The definition of St is given by
denotes an arbitrary function. In this Equation (1), we consider a normalised f, namely, the Strouhal number St, instead of f. The definition of St is given by
 . (2)
. (2)
All the symbols in Figure 6 represent the experimental results of St plotted against Re at L/s = 100 - 300, d/s = 1.2 - 1.4 and Re = 7000 - 20,000. While there exist minor random scatterings, these are not due to lower stability of the present periodic flow phenomenon but due to unknown factors included in the actual experimental apparatus. From the results, we can see the following three tendencies. That is, we can see that 1) St monotonically decreases with increasing L/s, that 2) St monotonically increases with increasing d/s and that 3) St monotonically increases with increasing Re. Then, we assume the following power function as .
.
 , (3)
, (3)
with experimental constants such as C = 0.068, α = −0.72, β = 1.37 and γ = 0.22. The experimental constants are determined using the least-squares method based on all the experimental results in Figure 6. We should note that L/s is the most influential upon St among the three non-dimensional governing parameters in the present test ranges. The curves in Figure 6 show this empirical formula Equation (3). We can see that the empirical formula almost agrees with the experiment.
The empirical formula Equation (3) is practically useful not only for the present FFJN in the present test ranges of the governing parameters, but restricted due to the lack of theoretical background. Then, we consider more generally focusing upon the jet-oscillation frequency. Figure 7(a) shows a typical example of the present experiments; that is, the time history of the pressure difference Δp between both the connecting tube ends at L/s = 100, d/s = 1.2 and Re = 13,000. The wave form in Figure 7(a) indicates some features which are commonly seen in all the present experiments; namely, 1) close periodicity with high-frequency random fluctuations and 2) the wave form characterised by the two similar non-isosceles triangles with positive and negative signs during each jet-oscillation period. The second feature is commonly observed, whenever the wave form is almost periodic. In fact, Fourier-transform analyses on the present results always are characterised by one remarkable and stable spectrum peak repre- senting a dominant periodicity, together with some secondary peaks representing higher harmonics due to the periodic but non-sinusoidal wave form. By means of simultaneous
Figure 6. Strouhal number St against Reynolds number Re, in regular FFJN oscillation. Symbols and lines denote experiments and an empirical formula, respectively.
Figure 7. Time histories of pressure difference Δp between both connecting-tube ends and velocity VT in a connecting tube, in regular FFJN oscillation at L/s = 100, d/s = 1.2 and Re = 13,000.
measurements, we get Figure 7(b), which is the corresponding time history of the flow velocity VT in the connecting tube obtained by the hot-wire anemometer (No. 13 in Figure 2). We can see that VT is closely periodic, as well as Δp. Again, the periodicity is not rigorous due to high-frequency random fluctuations superimposed. While the wave form of VT seems to be not sinusoidal but non-isosceles, it is rather different from the wave form of Δp in Figure 7(a).
Now, we summarise all the experiments concerning the pressure difference Δp from a quantitative point of view. Concerning the fluctuating period or the fluctuating frequency of Δp, we have already proposed Equation (3). Then, we next consider the fluctuating amplitude of Δp. To conclude, the pressure-difference-amplitude coefficient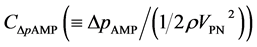 , which is the normalised half value of the difference
, which is the normalised half value of the difference  between the ensemble mean of the maximum Δp and the ensemble mean of the minimum Δp, almost keeps a constant value of about 0.11 through all the present measurements, being independent of L/s, d/s and Re.
between the ensemble mean of the maximum Δp and the ensemble mean of the minimum Δp, almost keeps a constant value of about 0.11 through all the present measurements, being independent of L/s, d/s and Re.
At this stage, we attempt to purify these wave forms by a simple model which is the same as Funaki et al. [31] . This is because, the experimental raw data including random fluctuations like Figure 7(a) and Figure 7(b) are not suitable for further delicate discussion on the switching mechanism of the jet. At first, Δp is simply modeled as a right-angled triangular wave, as shown in Figure 7(c). Then, using the modeled Δp, we compute VT, as shown in Figure 7(d). The computational procedure is as follows. As the compressibility is negligible through all the present experiments, the governing equations of motion can be described by
 , (4)
, (4)
where VT denotes the flow velocity averaged over a cross section of the connecting tube to be exact. λ is the resistance coefficient of pipe flow by Spriggs [32] and JSME [33] , and are defined as follows. If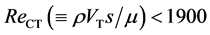 , then
, then
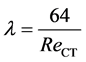 . (5)
. (5)
If 1900 ≤ ReCT < 2900, then

where γ = 9.8 × 10−4 ReCT − 1.852. And, if 2900 ≤ ReCT < 1,000,000, then

We numerically solve Equation (4) by the fourth-order Runge-Kutta method. To confirm numerical accuracy, we compare several computations with different time steps. As a result, we can see that the wave form of the computed VT in Figure 7(d) is almost the same as the experiment at one in Figure 7(b), not only qualitatively but also quantitatively. Of course, the periodicity in Figure 7(d) is rigorous, as the computed VT does not include randomly-fluctuating components.
Now, we consider the physical background of the present approach. We assume that the jet switches, when the accumulation of the inflow into a jet-switching side wall from the connecting tube through a control port, and/or of the outflow from the opposite un-jet-switching side wall into the other control port and the connecting tube, reaches a certain value. As the accumulation, we examine the time integral JP of mass flux, in addition to the time integral JM of momentum flux for comparison. As mentioned in Section 1, JM is proposed by Funaki et al. [31] . JP is the accumulated mass, which could be essentially regarded as the accumulated flow work by pressure to the fluid inside the re-circulation regions; strictly speaking, it is the product of the accumulated volume (or the quotient of the accumulated mass divided by ρ) and the pressure difference between a re-circulation region (Funaki et al. [19] ) and the connecting-tube end (or the chamber) on the same side. So, we hereinafter refer to JP as the accumulated flow work. Specifically speaking, the integrals JP and JM are defined as follows.


where VCP denotes the flow velocity at the control port. In Equation (8) and Equation (9), a decaying factor w is given by Equation (10).

where κ denotes a damping constant. We should note that these integrals are amounts per unit span. To specify the integral interval in Equation (8) and Equation (9), Figure 7(c) and Figure 7(d) show the definitions of t0 and tSW. At t = τSW, Δp jumps from zero to a positive value. This jump of Δp corresponds to the jet’s switching onto a side wall from the opposite side wall. On the other hand, VT is still negative even at t = τSW, that is, the fluid flows in the connecting tube from the jet-switching side to the opposite un-jet-switching side. Thereafter, Δp monotonically decreases with time t toward zero. On the other hand, VT monotonically increases with t toward a certain positive value, crossing zero at t = t0. Then, VT becomes positive at t > t0. In other words, the flow in the connecting tube is reversed at t = t0 and afterwards continues to accelerate. Finally, at t = tSW, Δp jumps from zero to a certain negative value, corresponding to the jet’s switching from the side wall on the jet-switching side onto the opposite side wall. And, VT begins to decelerate toward the next reverse of the connecting-tube flow from a certain positive value. In summary, there exists no reversed flow during the supposed integral interval in Equation (8) and Equation (9).
For convenience, all the integrals are usually normalised as follows.


Figure 8 shows the normalised integral 

Figure 8. Normalised integrals 

in the present study, we have confirmed that L/s is the most influential upon St among the three (also see Figure 6). So, we first examine the influence of L/s prior to d/s and Re.
At first, we see Figure 8(a). 




Second, we see Figure 8(b). 







To conclude, concerning the influences of the other two governing parameters d/s and Re in addition to the influence of L/s, we summarise all the results in the experimental ranges such as L/s = 100 - 300, d/s = 1.2 - 1.4 and Re = 7000 - 20,000 as follows. 1) κUNV is almost constant (≈0.012) being independent of both d/s and Re, 2) 


on the basis of 
As a result, the predicted St based on the empirical formula Equation (13) for 

As will be revealed in the latter half of the present study, the inflow from one control port on the jet-reattaching wall is crucial for jet switching, while the outflow into the other control port on the opposite jet-un-reattaching wall is not crucial. At the present stage, although we do not have exact information to discuss the details of the jet switching mechanism, it seems acceptable that to weaken/destabilize the re-circulation region on the jet-reattaching wall could be a trigger of the jet’s switching. In this context, the jet switching is possibly controlled by a certain accumulated amount from the control port, such as 







3.2. Single-Port Control
In the previous subsection, we have introduced 



At first, we need to characterise the inflow from a quantitative point of view. Then, we assume a constant acceleration of the inflow or the connecting-tube flow, and define the flow-increment-rate coefficient K as follows.

K means a normalised acceleration of fluid in the tube. From a theoretical point of view, K or the acceleration dVT/dt ought to be constant, but vary with time t. However, as seen in Figures 7(b)-(d), VT could increase approximately with a constant acceleration from the reversed time t0 to the jet-switching time tSW. In other words, we could suppose the connecting-tube flow and the inflow continue to accelerate linearly until the instant when the jet switches. Under this situation, K becomes an appropriate parameter.
Next, we estimate the range of K in the actual regular oscillation of the ordinary FFJN with two control ports. Figure 9 shows K plotted against Re, in the regular oscillation at L/s = 100 - 300 and Re = 5000 - 25,000. Figure 9(a) and Figure 9(b) denote the results at d/s = 1.2 and 1.4, respectively. More specifically, Figure 9 is based on the computed VT’s like Figure 7(d). We should note that K is the time-mean value from t0 to tSW, because K depends upon t in a strict sense. We can confirm the dependence of K upon L/s, d/s and Re. The actual range of K in the regular oscillation varies from 1 × 10−4 to 5 × 10−4. So, we next conduct the single-port-control experiments in a range of K from 1 × 10−4 to 3.5 × 10−4, keeping a constant acceleration of the inflow as closely as possible. To be exact, although K in the regular oscillation is not the same as that in the single-port-control experiments, the order of K is the same.
Figure 10 and Figure 11 show typical examples in the single-port-control experiment, namely, the time histories of two velocities VT and VEX and a pressure pTE where VEX and pTE denote the flow velocity near one side wall at the FFJN’s exit and the pressure at the connecting-tube end adjacent to the chamber and the control port. Figure 10 denotes the results at K = 1 × 10−4 and Re = 8800, and Figure 11 denotes those K = 3.5 × 10−4 and Re = 8800. In each figure, figures (a), (b) and (c) represent VT, VEX and pTE, respectively.
At first, we see Figure 10. In Figure 10(a), VT starts to increase from zero with time t at t = t0 (=0.6 s). We should note that the instant at t = 0 merely represents the time when each measurement starts. The increasing manner is not strictly linear, but almost linear with a constant acceleration during the duration t = 0.6 - 1.1 s. At t = tSW, the jet from the primary nozzle switches from the beforehand-jet-attached side to the opposite afterward-jet-attached side. In order to determine tSW, this switching is preliminarily observed by flow visualisation using smoke together with simultaneous measurements of VT, VEX, pTE and so on. Actually, corresponding to this jet switch at t = tSW, VEX in Figure 10(b) and pTE in Figure 10(c) step down and up toward constant values at the
Figure 9. Flow-increment-rate coefficient K against Re, in regular FFJN oscillation.
Figure 10. Time histories of velocities and pressure in single-port control at K = 1.0 × 10−4 and Re = 8800.
Figure 11. Time histories of velocities and pressure in single-port control at K = 3.5 × 10−4 and Re = 8800.
same time, respectively. Then, we can determine K or dVT/dt from Figure 10. To be exact, dVT/dt is time-mean which is obtained by such three data as t0, tSW and the VT at t = tSW. Of course, the above features can be seen in Figure 11 as well as Figure 10.
Figure 12 summarises all the results in the single-port-control: measured



4. Conclusion
In order to reveal the oscillation mechanism of a flip-flop jet nozzle (FFJN) with a connecting tube, we have carried out the measurements of pressures and velocities in the connecting tube and inside the FFJN specially focusing on the jet-oscillation frequency f, varying: 1) the diameter d of the connecting tube; 2) the length L of the connecting tube and 3) the jet velocity VPN from a primary-nozzle exit. Obtained results are as follows. We have proposed an empirical formula to determine f, and confirmed its validity. Then, to consider f more generally, we assume that the jet switches when a time integral reaches a certain value. At first, as the time integral, we have introduced the accumulated flow work 
Figure 12. Time histories of velocities and pressure in single-port control at K = 1 × 10−4 and Re = 20,000.
with two control ports in connection. As the result, we have confirmed good agreement between the single-port control and the regular jet oscillation. This agreement suggests that JP from the connecting tube to the FFJN inside can be a key parameter to explain the jet’s switching, in addition to the validity of JP in practical aspects to estimate the dominant jet frequency of the FFJN.
Cite this paper
Inoue, T., Nagahata, F. and Hirata, K. (2016) On Switching of a Flip-Flop Jet Nozzle with Double Ports by Single-Port Control. Journal of Flow Control, Measurement & Visualization, 4, 143- 161. http://dx.doi.org/10.4236/jfcmv.2016.44013
References
- 1. Levin, S.G. and Manion, F.M. (1962) Jet Attachment Distance as a Function of Adjacent Wall Offset and Angle. Fluid Amplification, 5, 20-22.
- 2. Ozaki, S. and Hara, Y. (1967) Introduction to Fluid Logic. Nikkan Kogyo Shimbun Ltd., Tokyo. (In Japanese)
- 3. Perry, C.C. (1967) Two-Dimensional Jet Attachment. In: Brown, F.T., Ed., Advances in Fluidics, ASME, New York, 205-217.
- 4. Epstein, M. (1971) Theoretical Investigation of the Switching Mechanism in a Bistable Wall Attachment Fluid Amplifier. ASME Journal of Fluids Engineering, 93, 55-62. http://dx.doi.org/10.1115/1.3425182
- 5. Drzewiecki, T.M. and Goto, J.M. (1973) An Analytical Model for the Response of Flueric Wall Attachment Amplifier. Fluidics Quarterly, 5, 43-65.
- 6. Wilson, M.P., Coogan, C.H. and Southall, K. (1970) Experimental Investigation of a Fluidic Volume Flowmeter. ASME Journal of Fluids Engineering, 92, 139-142. http://dx.doi.org/10.1115/1.3424922
- 7. Tippetts, J.R., Ng, H.K. and Royle, J.K. (1973) A Fluidic Flowmeter. Automatica, 9, 35-45. http://dx.doi.org/10.1016/0005-1098(73)90010-1
- 8. Viets, H. (1975) Flip-Flop Jet Nozzle. AIAA Journal, 13, 1375-1379. http://dx.doi.org/10.2514/3.60550
- 9. Morris, G.J., Jurewicz, J.T. and Palmer, G.M. (1992) Gas-Solid Flow in a Fluidically Oscillating Jet. ASME Journal of Fluids Engineering, 114, 362-366. http://dx.doi.org/10.1115/1.2910038
- 10. Raman, G., Hailye, M. and Rice, E.J. (1993) Flip-Flop Jet Nozzle Extended to Supersonic Flows. AIAA Journal, 31, 1028-1035. http://dx.doi.org/10.2514/3.11725
- 11. Raman, G. and Rice, E.J. (1994) Development of Phased Twin Flip-Flop Jets. ASME Journal of Vibration and Acoustics, 116, 263-268. http://dx.doi.org/10.1115/1.2930423
- 12. Raman, G., Rice, E.J. and Cornelius, D.M. (1994) Evaluation of Flip-Flop Jet Nozzle for Use as Practical Excitation Devices. ASME Journal of Fluids Engineering, 116, 508-515. http://dx.doi.org/10.1115/1.2910306
- 13. Raman, G. (1997) Using Controlled Unsteady Fluid Mass Addition to Enhance Jet Mixing. AIAA Journal, 35, 647-656. http://dx.doi.org/10.2514/2.185
- 14. Camci, C. and Herr, F. (2002) Forced Convection Heat Transfer Enhancement Using a Self- Oscillating Impinging Planar Jet. ASME Journal of Heat Transfer, 124, 770-782. http://dx.doi.org/10.1115/1.1471521
- 15. Hung, C.I., Wang, K.C. and Chyou, C.K. (2005) Design and Flow Simulation of a New Micromixer. JSME International Journal Series B, 48, 17-24. http://dx.doi.org/10.1299/jsmeb.48.17
- 16. Gregory, J.W., Sullivan, J.P. and Raghu, S. (2005) Visualization of Jet Mixing in a Fluidic Oscillator. Journal of Visualization, 8, 169-176. http://dx.doi.org/10.1007/BF03181660
- 17. Gregory, J.W., Sullivan, J.P., Raman, G. and Raghu, S. (2007) Characterization of the Microfluidic Oscillator. AIAA Journal, 45, 568-576. http://dx.doi.org/10.2514/1.26127
- 18. Yang, J.T., Chen, C.K., Tsai, K.J., Lin, W.Z. and Sheen, H.J. (2007) A Novel Fluidic Oscillator Incorporating Step-Shaped Attachment Walls. Sensors and Actuators A: Physical, 135, 476-483. http://dx.doi.org/10.1016/j.sna.2006.09.016
- 19. Funaki, J., Matsuda, Y., Inoue, T., Tanigawa, H. and Hirata, K. (2007) UVP Measurements on Periodic Flow in a Flip-Flop Jet Nozzle. Journal of Fluid Science and Technology, 73, 133-138.
- 20. Cerretelli, C. and Kirtley, K. (2009) Boundary Layer Separation Control with Fluidic Oscillators. ASME Journal of Turbomachinery, 131, Article ID: 041001. http://dx.doi.org/10.1115/1.3066242
- 21. Tesar, V., Zhong, S. and Rasheed, F. (2013) New Fluidic-Oscillator Concept for Flow-Se- paration Control. AIAA Journal, 51, 397-405. http://dx.doi.org/10.2514/1.J051791
- 22. Metka, M. and Gregory, J.W. (2015) Drag Reduction on the 25-deg Ahmed Model Using Fluidic Oscillators. ASME Journal of Fluids Engineering, 137, Article ID: 051108. http://dx.doi.org/10.1115/1.4029535
- 23. Yamasaki, H., Takahashi, A. and Honda, S. (1988) A New Fluidic Oscillator for Flow Measurement. Proceedings of FLUCOM, Sheffield, 1988, 16-20.
- 24. Shakouchi, T. (1989) A New Fluidic Oscillator, Flowmeter, without Control Port and Feedback Loop. ASME Journal of Dynamic Systems, Measurement, and Control, 111, 535- 539. http://dx.doi.org/10.1115/1.3153085
- 25. Mi, J., Nathan, G.J. and Luxton, R.E. (2001) Mixing Characteristics of a Flapping Jet from a Self-Exciting Nozzle. Flow, Turbulence and Combustion, 67, 1-23. http://dx.doi.org/10.1023/A:1013544019463
- 26. Priestman, G.H. and Boucher, R.F. (2005) The Biased Laminar By-Pass Fluidic Flowmeter. ASME Journal of Fluids Engineering, 127, 1199-1204. http://dx.doi.org/10.1115/1.2060729
- 27. Priestman, G.H. and Boucher, R.F. (2006) Smart Fluidic Meters for Simultaneous Measurement of Fluid Flowrate, Reynolds Number, Density and Viscosity. Journal of Chemical Engineering of Japan, 39, 383-393. http://dx.doi.org/10.1252/jcej.39.383
- 28. Huang, R.F. and Chang, K.T. (2007) Evolution and Turbulence Properties of Self-Sustained Transversely Oscillating Flow Induced by Fluidic Oscillator. ASME Journal of Fluids Engineering, 129, 1038-1047. http://dx.doi.org/10.1115/1.2746905
- 29. Hirata, K., Matoba, N., Naruse, T., Haneda, Y. and Funaki, J. (2009) On the Stable-Oscilla- tion Domain of a Simple Fluidic Oscillator. Journal of Fluid Science and Technology, 4, 623-635. http://dx.doi.org/10.1299/jfst.4.623
- 30. Hirata, K., Inoue, T., Haneda, Y., Miyashita, N., Tanigawa, H. and Funaki, J. (2011) On Dominant Oscillation Frequency of a Simplified Fluidic Oscillator. Journal of Fluid Science and Technology, 6, 534-547. http://dx.doi.org/10.1299/jfst.6.534
- 31. Funaki, J., Mizuno, G., Kondo, M. and Hirata, K. (1999) Oscillation Mechanism of a Flip- Flop Jet Nozzle Based on the Flow Which Flows through a Connecting Tube. Transactions of the JSME, Series B, 65, 928-933. (In Japanese) http://dx.doi.org/10.1299/kikaib.65.928
- 32. Spriggs, H.D. (1973) Comments on Transition from Laminar to Turbulent Flow. Industrial and Engineering Chemistry Fundamentals, 12, 286-290. http://dx.doi.org/10.1021/i160047a004
- 33. The Japan Society of Mechanical Engineers, Ed. (1979) JSME Data Handbook: Hydronic Losses on Pipes and Ducts, JSME, Tokyo, 22-26. (In Japanese)
Nomenclature
A: aspect ratio of a primary-nozzle throat, º S/s
b: breadth of a control port (m)
CΔpAMP: coefficient of pressure-difference amplitude º ΔpAMP/(1/2 ρVPN2)
d: (inner) diameter of a connecting tube (m)
f: frequency (Hz)
GSW: gap between side walls (m)
JM: time integral of momentum flow per unit span (kg/s)
JP: time integral of mass flow per unit span (kg/m)
K: flow-increment-rate coefficient
L: length of a connecting tube (m)
LSW: streamwise length of a side wall (m)
p: pressure (Pa)
Δp: pressure difference between two connecting-tube ends (Pa)
ΔpAMP: (half) amplitude of Δp (Pa)
Q: (volumetric) flow rate (m3/s)
Re: Reynolds number, º ρVPN s/μ
ReCT: connecting-tube Reynolds number, º ρVT d/μ
S: span (m)
s: spacing of a primary-nozzle throat (m)
St: Strouhal number, º f s/VPN
t: time (s)
V: flow velocity (m/s)
w: decaying factor
λ: friction coefficient of pipe
κ: damping constant
μ: viscosity of fluid (Pa∙s)
ρ: density of fluid (kg/m3)
τSW: time at former jet’s switching (s)















