Journal of Flow Control, Measurement & Visualization
Vol.04 No.01(2016), Article ID:62027,17 pages
10.4236/jfcmv.2016.41002
Flow Visualization of Multi-Hole Film-Cooling Flow under Varying Freestream Turbulence Levels
Timothy W. Repko, Andrew C. Nix, S. Can Uysal, Andrew T. Sisler
Department of Mechanical and Aerospace Engineering, West Virginia University, Morgantown, WV, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 1 July 2015; accepted 7 December 2015; published 18 December 2015

ABSTRACT
A flat plate film cooling flow from a multi-exit hole configuration has been numerically simulated using both steady and unsteady Reynolds Averaged Navier Stokes (RANS and URANS) Computational Fluid Dynamics (CFD) formulations. This multi-exit hole concept, the Anti-Vortex Hole (AVH), has been developed and studied by previous research groups and shown to mitigate or counter the vorticity generated by conventional holes resulting in a more attached film cooling layer and higher film cooling effectiveness. The film cooling jets interaction with the free stream flow is a long studied area in gas turbine heat transfer. The present study numerically simulates the jet interaction with the multi-exit hole concept at a high blowing ratio (M = 2.0) and density ratio (DR = 2.0) in order to provide a more detailed, graphical explanation of the improvement in film cooling effectiveness. This paper presents a numerical study of the flow visualization of the interaction of film cooling jets with a subsonic crossflow. The contour plots of adiabatic cooling effectiveness were used to compare the multi-exit hole and conventional single hole configurations. The vortex structures in the flow were analyzed by URANS formulations and the effect of these vortices on the cooling effectiveness was investigated together with the coolant jet lift-off predictions. Quasi-Instantaneous Temperature Isosurface plots are used in the investigations of the effect of turbulence intensity on the cooling effectiveness and coolant jet coverage. The effect of varying turbulence intensity was investigated when analyzing the jets’ interaction with the cross flow and the corresponding temperatures at the wall. The results show that as the turbulence intensity is increased, the cooling flow will stay more attached to the wall and have more pronounced lateral spreading far downstream of the cooling holes.
Keywords:
Film Cooling, Flow Visualization, Heat Transfer, Gas Turbines, Turbulence

1. Introduction
Film cooling is an extensively studied method for cooling of gas turbine hot section airfoils. Increases in the maximum operating temperature of the turbine lead to increases in the power output and thermal efficiency of the turbine engine, but cause decreases in the durability for the components in the hot section of the engine. In order to allow for higher operating temperatures and improved component durability, film cooling is employed to protect the components from the hot mainstream gas, and to keep the temperatures of the components within acceptable ranges.
Film cooling studies often demonstrate effectiveness of cooling in experimental and computational studies with contour plots of film-cooled component surface non-dimensional temperatures, and streamwise variation plots of centerline and spanwise averaged adiabatic effectiveness. While this information is extremely useful, it is highly desirable for gas turbine engineers to have an in-depth understanding of the film cooling flow physics to better design cooling schemes that allow for the most efficient gas turbine cycle.
CFD software offer users a wide variety of flow visualization tools that can be used to visualize the flow field in a custom level of detail that may not be obtained with current experimental techniques. In literature, there are such examples primarily for conventional hole flow analysis but there are also some recent studies for multi- hole concepts, such as the Anti-Vortex Hole (AVH). In the numerical study by Kim et al. [1] Detached Eddy Simulation solvers were used to visualize the flow field of a conventional single film cooling hole, in which the visualizations through temperature contours, velocity vectors and vortical structures were used to investigate the effect of Counter Rotating Vortex (CRV), jet lift-off and turbulent mixing on the cooling effectiveness. Kalghatigi et al. [2] used the Large Eddy Simulation (LES) technique to solve for the flow field generated from a single conventional hole and made a dynamic mode decomposition analysis to investigate the dominant vortex frequencies that affect the film cooling effectiveness. Flow visualization obtained by LES simulations was used to analyze the entrainment of cross flow by the CRV and the visualization of vortical structures allowed them to relate the temperature distribution with specific types of vortices generated from the delivery tube. Nemdili et al. [3] used the velocity vortex visualizations obtained from their numerical study on AVH holes to investigate the effects of different blowing ratios under a fixed high turbulence intensity. Yao et al. [4] used flow vector visualization, contour plots and temperature plots from their CFD study for a fixed turbulence intensity to explain how CRV effect is reduced and its effect on the increase of effectiveness with the usage of branched holes instead of using conventional holes under the same flow conditions. In this study presented herein, visualizations from the CFD simulations performed with Star-CCM+® (by CD-Adapco) with the AVH geometry are used to analyze the effects of increasing turbulence intensity and the reduction in CRV on the cooling effectiveness through temperature contours, velocity field plots, and 3D flow contours.
The current study presents the results of numerical study to visualize a multi-hole concept, the anti-vortex hole (AVH) that has been documented in previous studies [5] -[7] . The anti-vortex hole concept is shown in the current study as well as the previous studies to have its performance enhanced with elevated mainstream turbulence levels. Visualization of the flow field at varying turbulence levels is presented herein using 2-D and 3-D computational fluid dynamics (CFD) results.
2. Numerical Study
A control volume for the current study was selected consistent with previous studies in the open literature, to allow for comparison of the performance of a single hole, conventional film cooling geometry to the current AVH concept. A control volume is selected to encompass the region of influence of a single film-cooling hole.
Results from Repko et al. [5] showed that varying the turbulent length scale does not have a major effect on the cooling effectiveness of the AVH, resulting in a reduction in the number of cases that are needed for comparison of different turbulence levels. Three different cases of varying turbulence intensity were studied by using both steady and unsteady Reynolds Averaged Navier Stokes (RANS and URANS) solvers in order to be able to analyze and compare the differences in the flow predictions by two different solution techniques. The cases are presented in Table 1.
As shown in the table, three separate cases are analyzed with RANS, while an additional case is analyzed for comparison purposes using URANS.
2.1. Film Cooling Geometry
The anti-vortex hole (AVH) geometry was developed by Heidmann et al. [6] and could possibly, though optimization reduce or counter the vorticity of the counter rotating vortex that exists in conventional straight and even shaped hole film cooling schemes. The geometry examined in this study was selected from the study by Dhungel et al. [7] that compared six different anti-vortex hole geometries. The geometry for this study was selected as the best performing cooling geometry as well as the most practically machined geometry from the six cases previously tested. The geometry is shown together with the geometric parameters in Figure 1.
The control volume used was identical to the ones used in previous work [5] -[9] , for the ease of direct comparison of the results. This control volume is determined such that the region of influence of a single hole is successfully encompassed. As presented in Figure 2, all of the dimensions of the control volume were normalized with respect to the main hole diameter (dm) of the AVH. This control volume is used in steady RANS analyses, which is a representation of half of the full domain. A symmetry plane is defined at the main hole centerline and with this method it is expected to have an adequate flow field, which also allows reduced computation times, because there is no cross flow is expected in steady RANS cases. In the unsteady work, however, the full control volume domain is used in order to account for the unsteady flow crossing the plane along the main hole centerline.
Table 1. Test matrix for comparison of RANS and URANS flow field visualization results.
Figure 1. Three view drawing and geometric parameters of Anti Vortex Hole (AVH) used in the analysis [6] .
2.2. Computational Grid
A multi-block structured hexahedral grid was produced using GridProTM for the three turbulence condition cases. This grid contained 2.5 million hexahedral cells and employed viscous clustering near to the solid walls with a y+ value less than 1.0 at all locations. Nominally the y+ value was on the order of 0.1 at nearly all locations along the top surface. A stretching ratio of 1.2 was used normal to the viscous walls in conjunction with standard CFD practice for film cooling studies. A symmetry boundary condition was used on sides. Figure 3 shows the boundary conditions and structured multi-block grid created in GridProTM, with each block indicated by a different color.
The top plane extends 10 hole diameters above the test surface and has been assumed to be sufficiently high enough to be considered a symmetry plane. The width of the full control volume of the AVH is 3 hole diameters from the symmetry plane to opposite symmetry plane as shown in Figure 2. A symmetry plane was introduced at the main hole centerline, and the domain extends 1.5 hole diameters in width to the outer symmetry plane. Only half of the full domain was modeled for the RANS simulations, while the full domain was necessary for the URANS simulations.
The grid used in the unsteady RANS analyses were created by using trimmed hexahedral grid option of Star-CCM+. This option creates a hexahedral mesh that is nearly in line with the free stream flow direction and expected to produce results in high accuracy in those areas. Viscous clustering was employed at the near wall locations with y+ value of near 1.0. An additional level of mesh refinement was also made around the cooling jet region by increasing the mesh density in a box shaped volume shown in Figure 4. The resulting enclosed cells were 60 percent of the base mesh size in this area. The resultant mesh for the unsteady cases contained 4.5 million cells.
The aforementioned grid was the “fine” grid taken from the CFD study by Heidmann [8] , in which two versions of the same mesh were generated with two different densities. A grid independence study with this mesh was carried out by using 1.2, 2.5 and 3.0 million cells through the comparison of centerline effectiveness values obtained from a probe defined to be passing through the centerline of the cooled surface. The comparison of the results is shown in Figure 5.
Figure 2. Control volume definition employed in the analyses.
Figure 3. Computational grid used in steady RANS cases.
Figure 4. Computational grid used in unsteady RANS analyses.
Figure 5. Grid independence study comparing centerline effectiveness.
Figure 5 shows a good agreement of the centerline effectiveness predictions with increased mesh density. Grid independence was concluded due to the difference of the results from all meshes having less than 10% difference. The 2.5 million cell case was chosen to be used in this analysis by considering the overall solution wall- clock time.
2.3. Numerical Simulation Parameters
The ratio of the static pressure of the outlet to the total pressure of the inlet was set to the isentropic value of p/p0 = 0.9725 to produce a nominal Mach number of 0.2 in the freestream flow. The plenum total pressure was set approximately 8 percent higher than the inlet total pressure to produce a blowing ratio (BR) of 2.0. The plenum total temperature was set to 0.5 times the freestream total temperature to provide a temperature difference considered representative of engine conditions [8] . A turbulence intensity of 1% and a length scale normalized by main cooling hole diameter of 1.0 was specified for the plenum. A Reynolds number based on the main film cooling hole diameter and mainstream flow conditions of 11,300 was matched to previous work [5] [8] [9] .
The boundary conditions were shown on the geometry in Figure 3. These boundary conditions are the same for both steady and unsteady RANS cases. In the unsteady RANS case, the unsteady time step is included in order to be able to capture fluctuations or unsteady behavior in the mean quantities of the flow. The time step used in both RANS cases was chosen to be 1 μs, which allowed for a CFL condition to be less than 1.0.
The k-ω turbulence model is used in the analyses with the turbulence intensities described in Table 1 and using the fixed length scale of 1 main hole diameter (Lx/dm = 1). The convergence criteria in the present analyses had a reduction in all residuals by 3 orders of magnitude with no observable change in the surface temperature prediction downstream of the holes for 1000 iterations. This was accomplished by using area-averaged monitors of the surface temperature as well as three hole diameters (3dm) off of the surface.
3. Results and Discussion
The primary goal of this paper is to document efforts to visualize the coolant jet with both RANS and URANS formulations to analyze the interaction of the jets with a subsonic crossflow and the influence of freestream turbulence on the ability of the coolant jet to remain attached to the surface and provide cooling coverage. The results will employ contour plots of dimensionless temperature, vector plots of velocity and isosurfaces of dimensionless temperature generated both in RANS and URANS numerical formulations to accomplish this goal.
3.1. Contour Plots of Effectiveness
One of the primary analysis methods for the effectiveness of turbine film cooling is through inspections of contour plots of adiabatic wall surface temperature non-dimensionalized into adiabatic effectiveness (Equation (1)).
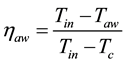 (1)
(1)
Figure 6 is shown to illustrate the typical coverage of a straight 30˚ inclination film cooling hole flow at high blowing ratio under varying turbulence conditions [9] . The hole diameter and Reynolds number and the plenum condition from this past study are consistent with the current work. It can be seen that there is a large amount of area downstream of a hole that is not covered at all by the coolant, which is typical of straight cooling holes and has been studied extensively in previous work [7] [10] -[16] . The hole spacing is three hole diameters as is consistent with practice in real engines for cylindrical holes.
An AVH geometry has a much better coolant coverage than the straight film cooling hole case at high blowing ratio. Figure 7 shows contour plots of the computed adiabatic effectiveness for the test surface with an AVH hole, for all three turbulence cases (as reported in Table 1), mirrored across the main hole centerline for clarity in the RANS cases. Similar to Figure 6, the hole spacing is three hole diameters.
Dhungel et al. [7] reported that for a single hole geometry case, similar to that shown in Figure 6, the cooling hole effectiveness reduces as the blowing ratio is increased from 1.0 to 2.0. A study conducted by Kim and Hassan [1] with a single hole geometry by using RANS and URANS simulations with blowing ratio 1.0 showed that the predicted maximum cooling effectiveness along the centerline was less than 0.5 and this occurs only at a limited x/d region. The cooling provided by the AVH geometry, however, has higher effectiveness values in a wider region as shown in Figure 7, which illustrates that the AVH concept has much better downstream coverage and lateral spreading of the coolant than a single hole under the same coolant mass flow conditions. The improved coolant coverage of the AVH geometry in relation to the single hole configuration is achieved by the two side holes, which alleviate trapping of hot gases close to the surface as a result of the counter rotating vortex (CRV). The comparison of Figure 6 and Figure 7 show a clear improvement in the coolant flow coverage from a single hole geometry to the AVH geometry. For the low turbulence cases, the lateral spreading of the coolant downstream of the hole is less prominent than in the higher turbulence cases. This is highlighted by a black oval
Figure 6. Contour plots of adiabatic effectiveness showing typical film cooling coverage of a single cooling hole at high Blowing Ratio (BR = 2) [9] .
shown in the top contour plot with the lowest turbulence intensity and smallest length scale. As the turbulence intensity increases the lateral spreading of the coolant occurs much further upstream and provides better coverage and thermal protection than at lower turbulence intensities. A region of interest in between the main and side holes highlighted in the figure shows a “hot streak”. This hot streak is shortened with increasing turbulence intensity, as can be shown by comparing the black oval shown in the bottom contour plot to the longer oval in the top contour plot [10] . Trends showing improvement to the cooling effectiveness with increasing turbulence intensity match the trends for cylindrical holes at high blowing ratio found in Bons et al. [11] and the trends found for shaped holes found in Saumweber et al. [12] [13] .
In a film cooling flow, the momentum of the coolant jet causes the jet flow to lift off from the surface and the interaction of this cylindrical coolant jet with the main flow causes eddy structures to occur as in a crossflow around a cylinder. Although both RANS and URANS solvers both predict higher effectiveness with increasing turbulence, the predictions for surface temperature distributions are not the same due to these unsteady interactions caused by eddies, as shown in Figure 7. In order to visualize the vortex shedding and eddy structures in the unsteady compared to steady predictions, the absolute difference between the quasi-instantaneous URANS and the averaged URANS was determined. The averaged URANS values were calculated by using an ensemble average across a large range of time steps. The result of this analysis for a moderate freestream turbulence case is shown in Figure 8.
From the results in Figure 8, unsteady flow structures can be seen in the wake of the cooling holes with alternating cool and hot spots convecting downstream. These structures are a result vortex shedding around a cylinder of diameter dm and flow pulsations within the cooling hole (discussed in Section 3.3). These flow structures weaken around 10 to 15 diameters, and nearly disappear after 15 diameters away from the cooling holes.
Figure 7. Contour plots of adiabatic effectiveness showing film cooling coverage of the AVH at high Blowing Ratio (BR = 2) for different turbulence levels.
Figure 8. The contour plot of the difference between Quasi-Instantaneous URANS and Time Averaged URANS film effectiveness to show the vortical structures in the flow field (Tu = 10%, Λx/dm = 1).
The differences caused by the predictions of flow unsteadiness by URANS simulations primarily affect the cooling effectiveness results in the near-hole region, which is the region of interest that governs the physics that controls the cooling performance of the geometry. This is also shown by Kim and Hassan [1] , that the flow physics near the hole region is more accurately represented by unsteady RANS solutions than steady RANS solutions because the region of unsteady effects is dominant over the region of steady flow near the coolant hole. This is a driving force in the cooling performance because the way that the cooling flow exits the hole geometry dictates the way that the coolant flows downstream, and hence how it influences the cooling of the surface.
3.2. Visualization of Counter Rotating Vortices
In film cooling cases with high blowing ratios (ratios greater than 1.5), which are generally seen in real engine applications, the cooling flow may detach from the surface resulting in lift off of the jet from the surface. In such a case, a counter rotating vortex (CRV) pair is created inside of the jet, which reduces the cooling effectiveness because of the entrainment of hot gases from the free stream flow to the wall surface. This phenomenon is described schematically by Haven et al. [14] and can be seen in Figure 9.
The concept of Anti-Vortex Hole (AVH) was developed by Heidmann et al. [6] in order to reduce this vortex effect by introducing two side holes that produce a strong upwash effect that is intended to balance the downwash on the outside of the main hole jet CRV or “kidney vortex”. This is the main difference between the AVH and single hole geometry. The introduction of the upwash effect from each of the side holes in an AVH configuration helps to mitigate the kidney-vortices, seen in Figure 8, that are formed downstream of a single film coolant hole. In an effort to visualize the flow and vortices of the jet in this configuration, the dimensionless temperature, given in Equation (2), were plotted at the discrete cross sectional planes downstream of the cooling hole.
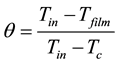 (2)
(2)
where Tfilm is a local temperature in the flow affected by the film cooling and not a bulk temperature, Tin is the mainstream inlet temperature and Tc is the coolant temperature. The dimensionless temperature for a representative RANS case is presented for four discrete cross sectional planes in an isometric view shown in Figure 10. Immediately downstream of the AVH there is as light detachment zone where there is little mixing of the coolant from the side holes and the main hole. As the flow progresses downstream the coolant from the side holes mixes with the coolant from the main hole and begins to flatten out and cool the wall across the entire domain. The CRV seems to be reduced as the centerline cooling flow does not fully detach.
Combining the contour plots of dimensionless surface temperature with velocity vectors tangential to the streamwise direction allows for visualization of improvement in the cooling effectiveness with the reduction of the vortices (CRV) by the side holes. As the flow progresses downstream, the downwash created by the main
Figure 9. Diagram depicting the Counter Rotating Vortex (CRV) [14] .
Figure 10. Dimensionless temperature plots for 4 discrete streamwise locations.
hole jet vortex (CRV) is reduced by the counter vortices generated by the side holes, which results in improved cooling coverage at all streamwise locations, especially downstream, as shown in Figure 11. The reduction in vorticity as the flow progresses downstream acts to increase cooling, because the ability of vortices to circulate the hot mainstream flow towards the surface is reduced. As the freestream turbulence is increased, there is an increase in lateral spreading and more coolant in the near-wall region. In the near-hole region (x/dm = 3), the differences in vorticity between the low (5%) and high (20%) freestream turbulence cases is difficult to discern, however, as the flow progresses downstream, the reduction in vorticity at higher freestream turbulence conditions is apparent, especially at x/dm of 15 and 25.
Velocity vector plots in the near-hole region show that the upwash produced by the side holes is stronger than that of the main cooling hole, as shown in Figure 12 for the near-hole region (at a streamwise distance of x/dm = 3). This region is used to analyze the effect of the vorticity generated by the side holes, which is the location of interest because of the increased heat transfer to the wall between the holes demonstrated in previous work [10] . This strong upwash is then balanced later at further downstream locations by the downwash of the main cooling hole, which results in a better attached cooling layer. This can be seen from Figure 12, by comparing the velocity contour plots from 7, 15 and 25 hole diameters away from the main hole. Moving downstream, the vortices generated from both holes neutralize each other and as a result the flow field is more smooth as can be seen in the x/dm = 25 velocity profile. In the figure, due to the density of the velocity vectors, arrows illustrating the direction of rotation are included within the circles showing the core of the vortices. In the last image, at x/dm = 25, the large oval highlights the relative lack of vorticity compared to this region further upstream.
Figure 12 also shows that there is a minor difference between the RANS and URANS cases for their tangential velocity fields, with the URANS solution predicting stronger side hole vorticity at most streamwise locations. The figures shown are a snapshot of the URANS solution. Note that the core of the CRV appears to be at a different z/dm location and the CRV appears to be of lower intensity in the RANS case. In reality, this vortex core is fluctuating up and down, as a result of the pulsating nature of the coolant flow captured by URANS. This unsteadiness was discussed in the analysis of Figure 7 and Figure 8 earlier and is analyzed in the following section.
Figure 11. Dimensionless temperature contour plots are compared together with the velocity vector field plots showing the vortices for 4 discrete streamwise locations.
3.3. Visualization of Cooling Hole Flow
Visualization of the flow within the cooling hole, from the cooling feed plenum to the mainstream provides information about the pulsating nature of the film coolant injection creating a portion of the unsteadiness discussed earlier. According to Walters et al. [15] , the flow at the main coolant jet exit is affected by the recirculation generated within the main cooling hole and the interaction of the exiting jet with the crossflow. These two effects create the unsteadiness and the kidney vortices discussed in the previous sections. This recirculation and low momentum region has been studied by numerous research groups including Leylek et al. [16] and is shown schematically in Figure 13.
Figure 12. Velocity vector plots at 4 different streamwise (x/dm) locations showing the balancing of the vortices at further downstream location from the AVH (URANS solutions on the left, RANS solutions on the right).
Figure 13. Velocity vectors inside of a film cooling hole with overlaid schematic showing area of recirculation by Leylek et al. [16] .
The vortices, which are created due to the existence of the low momentum region in the main cooling hole as shown in Figure 13, shed off and convect downstream causing the fluctuation of the coolant jet. In order to observe this phenomenon, four line-integral convolutions of the velocity vectors were plotted in Figure 14 at a plane along the main hole centerline. From the figure, it can be deduced that the flow solutions gave accurate representation of the unsteadiness in the main cooling hole documented by Walters and Leylek [15] [16] . This figure depicts a time evolution of the cooling hole flow field, in which the black box outlines the evolution of eddies as it travels downstream of the hole and the white circle represents the center of an eddy. This eddy is shown in the figure to be convecting upward and to the right within the domain outlined by the black box. The contours display the velocity magnitude tangential to the plane. The interaction between the low momentum region and the jetting effect has a significant effect on the main cooling flow. Depending on engine conditions, the conditions at the plenum will be a driving factor for how cooling flow travels through the holes and into the main cooling flow field.
As a result of having this jetting effect, the main cooling hole jet is lifted off from the surface and reattached to the surface 5 - 10 hole diameters (x/dm) downstream, depending on the turbulence level as observed in Figure 6. In order to observe the jet lift-off, which is a primary factor affecting the cooling effectiveness negatively, non-dimensional temperature plots were generated in a vertical plane through the main hole centerline in Figure 15. The figure illustrates results from steady RANS, URANS and URANS averaged solution techniques. A comparison between different solution techniques showed that in the unsteady case there is a slightly greater prediction of lift-off for the URANS simulations along the main coolant jet compared to the steady case. There is a slight but noticeable increase in the jet lift-off for the URANS when comparing the RANS on the top to the averaged URANS in the middle. This is highlighted in the region enclosed by identically sized and positioned black ovals. Instantaneous URANS is also shown in Figure 15 for a qualitative view of the instantaneous behavior of the main coolant jet as a comparison to the averaged URANS and RANS dimensionless temperature field, in order to observe the expected fluctuating jet flow due to the vortex shedding in the cross flow.
The coolant jet appears to follow a more pronounced parabolic trajectory in the URANS case than in the RANS case. In the URANS case, the coolant is able to penetrate further into the main stream than in the case for the steady analysis. It should be noted that the difference in the results of the two methods may also come from
Figure 14. Line integral convolution of main hole centerline at 4 different time levels showing the pulsating nature of the flow leaving the main hole (Tu = 20%, ΛX/dm = 1).
Figure 15. Dimensionless temperature contour plots in the mid-vertical plane passing through the main hole centerline are compared for different solution techniques (Tu = 10%, ΛX/dm = 1).
the differences between the solution methodologies of steady and unsteady techniques, and the exact location of coolant flow reattachment is sensitive to the solution technique used.
3.4. 3-D Contours of Flow (Isosurfaces)
In order to analyze how the coolant jets are interacting and mixing with the mainstream flow as they convect downstream, quasi-instantaneous dimensionless temperature isosurface contours were plotted. In a sense, this allows for visualization of the 3-D “shape” of the coolant jet.
In order to analyze the effect of freestream turbulence intensity on the coolant jet, the mixing of the coolant streams can be visualized by way of the dimensionless temperature isosurfaces. Isosurfaces for three different freestream turbulence levels (Tu = 5, 10% and 20%) are shown in Figure 16.
It is clearly seen that the film layer becomes more attached to the wall as the turbulence intensity is increased. In the lowest turbulence case the main and secondary jets are able to penetrate further into the mainstream flow than the higher turbulence cases. The lowest turbulence case also has the worst lateral spreading of the coolant, whereas the highest turbulence intensity has the best lateral spreading of the coolant. The pulses stemming from the recirculation region in the main cooling hole are apparent when looking at the isosurfaces. These pulses are more distinct in the lowest turbulence case and they propagate further downstream before being damped out. At the highest turbulence intensity the coolant from the main or side holes does not penetrate as far into the freestream as compared to the low turbulence case. The highest turbulence case shows the best attachment of the coolant to the surface and the best overall coverage downstream of the cooling holes. This qualitatively confirms the results discussed from the contour plots of non-dimensional surface temperature presented earlier. This affects the lateral spreading of the coolant flow, which improves as the turbulence intensity is increased, resulting in better cooling effectiveness at high turbulence intensities.
According to Bons et al. [11] , the point at which the flow from adjacent cooling holes merges is at an earlier location in high turbulence intensity levels, since the energy of high turbulence intensity flows reduces the vertical dissipation of the coolant flow more and the flow tends to spread laterally in these cases. This also causes the film cooling flow to attach to the surface at an earlier streamwise location than in low turbulence intensity cases. As the Anti-Vortex Hole case is considered, the three streams exiting from the holes are all affected by the main stream flow equally, resulting in the reduced vertical penetration and increased lateral spread as the turbulence intensity of the main stream flow is increased.
Figure 16. Isosurface plots of dimensionless temperatures and the adiabatic effectiveness surface contour plots are compared for three different turbulence intensities by URANS solutions (ΛX/dm = 1).
4. Conclusions
This paper presents a numerical study of the flow visualization of the interaction of multi-hole film cooling jets with a subsonic crossflow employing both RANS and URANS methodology. The effect of freestream turbulence intensity was investigated when analyzing the jet interaction with the cross flow and the corresponding temperatures at the wall. The results show that as the freestream turbulence intensity is increased, the cooling flow will stay more attached to the wall, providing improved coolant coverage and higher cooling effectiveness. This is evident from contour plots of non-dimensional temperature (film cooling effectiveness) and is validated through visualization of the cooling jet flow progression through velocity vectors and isosurfaces of temperature, which is the main focus of this work.
In both RANS and URANS analyses, the resulting contour plots of cooling effectiveness demonstrate the advantage of the AVH over a conventional single hole configuration due to the generation of vortices by the side holes of the AVH intended to mitigate the counter-rotating vortex (CRV) pair generated by the main hole. This improvement in film cooling effectiveness from the single hole cases to the AVH cases, as a result of the change in flow structure, is an important conclusion gained from this study. In the region between the side hole and the main hole, a vortex is generated from the side hole having opposite sense (direction of rotation) compared to the nearest vortex from the main hole kidney vortex. This opposing vortex from the side hole counteracts and mitigates the effect of the nearest kidney vortex, resulting in a reduction in entrainment of the hot mainstream flow toward the surface. As a result, the reduction in strength of the counter rotating vortices from the side holes improves the cooling film coverage on the surface. The dimensionless temperature plots obtained with both solution techniques demonstrate this effect on the surface temperature distribution and show how the cooling jets merge in a shorter distance under higher freestream turbulence, reducing “hot streaks” between the cooling holes. However, URANS solutions provide a more accurate representation of the surface temperature distribution, especially in the near hole region, because the dominance of the unsteady flow affects within this region.
The unsteadiness in and close to the exit of the cooling holes was realized in the URANS solver. Plots of velocity within the cooling hole and isosurfaces of temperature downstream of the coolant hole demonstrated pulsations in the coolant jet flow that result from vortex shedding around the main hole coolant jet and from flow separation and the jetting effect within the cooling hole between the coolant feed plenum and the hole exhaust to the mainstream.
The mixing of the coolant jets was analyzed by using the quasi-instantaneous dimensionless temperature isosurfaces obtained by URANS solutions. The unsteady flow analysis illustrated a difference in the predictions of coolant jet lift-off and reattachment compared to steady analysis. The results of URANS analysis show that as the turbulence intensity is increased the coolant flow is reattached to the surface at a closer location to the main hole, resulting in an improved film coverage and increased overall cooling effectiveness. The cooling effectiveness downstream is also improved because of the reduction of vortical structures, which were reduced with increasing freestream turbulence intensity, and improved lateral spreading of the coolant.
Acknowledgements
The authors would like to acknowledge the support of the Department of Energy, Office of Science, Experimental Program to Stimulate Competitive Research (EPSCoR) under grant/contract number DE-FG02-09ER46615, monitored by Dr. Tim Fitzsimmons of the DOE Office of Science/EPSCoR. The authors would also like to thank CD-ADAPCO for their software training and support throughout this analysis.
Cite this paper
Timothy W.Repko,Andrew C.Nix,S. CanUysal,Andrew T.Sisler, (2016) Flow Visualization of Multi-Hole Film-Cooling Flow under Varying Freestream Turbulence Levels. Journal of Flow Control, Measurement & Visualization,04,13-29. doi: 10.4236/jfcmv.2016.41002
References
- 1. Kim, S.I. and Hassan, I. (2010) Unsteady Simulations of a Film Cooling Flow from an Inclined Cylindrical Jet. Journal of Thermophysics and Heat Transfer, 24, 145-155. http://dx.doi.org/10.2514/1.33167
- 2. Kalghatigi, P. and Acharya, S. (2014) Modal Analysis of Inclined Film Cooling Jet Flow. ASME Journal of Turbomachinery, 136, 081007-1-081007-11. http://dx.doi.org/10.1115/1.4026374
- 3. Nemdili, F., Nemdili, S. and Azzi, S. (2013) Numerical Investigation on Film Cooling Effectiveness Using the Anti-Vortex Concept. 21ème CongrèsFrançais de Mécanique.
- 4. Yao, Y., Zhang, J. and Yang, Y. (2012) Numerical Study on Film Cooling Mechanism and Characteristics of Cylindrical Holes with Branched Jet Injections. Propulsion and Power Research, 2, 30-37. http://dx.doi.org/10.1016/j.jppr.2012.12.001
- 5. Repko, T.W., Nix, A.C. and Heidmann, J.D. (2013) A Parametric Numerical Study of the Effects of Freestream Turbulence Intensity and Length Scale on Anti-Vortex Film Cooling Design at High Blowing Ratio. ASME Paper HT2013-17255.
- 6. Heidmann, J.D. and Ekkad, S.V. (2007) A Novel Anti-Vortex Turbine Film Cooling Hole Concept. ASME Paper GT2007-27528. http://dx.doi.org/10.1115/gt2007-27528
- 7. Dhungel, A., Lu, Y., Phillips, W., Ekkad, S.V. and Heidmann, J.D. (2007) Film Cooling from a Row of Holes Supplemented with Anti-Vortex Holes. ASME Paper GT2007-27419.
- 8. Heidmann, J.D. (2008) A Numerical Study of Anti-Vortex Film Cooling Designs at High Blowing Ratio. ASME Paper GT2008-50845. http://dx.doi.org/10.1115/gt2008-50845
- 9. Hunley, B.K., Nix, A.C. and Heidmann, J.D. (2010) A Preliminary Numerical Study on the Effect of High Freestream Turbulence on Anti-Vortex Film Cooling Design at High Blowing Ratio. ASME Paper GT2010-22077. http://dx.doi.org/10.1115/gt2010-22077
- 10. Repko, T.W. (2014) Numerical Investigation of the Influence of Elevated Freestream Turbulence Levels on the Cooling Effectiveness of an Anti-Vortex Hole Geometry. MS Thesis, West Virginia University, Morgantown, West Virginia.
- 11. Bons, J.P., Macarthur, C.D. and Rivir, R. (1996) The Effect of High Freestream Turbulence on Film Cooling Effectiveness. ASME Journal of Turbomachinery, 118, 814-825. http://dx.doi.org/10.1115/1.2840939
- 12. Saumweber, C., Schultz, A. and Wittig, S. (2002) Free-Stream Turbulence Effects on Film Cooling with Fan Shaped Holes. ASME Paper GT2002-30170.
- 13. Saumweber, C. and Schultz, A. (2012) Free-Stream Effects on the Cooling Performance of Cylindrical and Fan-Shaped Cooling Holes. ASME Journal of Turbomachinery, 127, 061007-1-061007-12. http://dx.doi.org/10.1115/1.4006287
- 14. Haven, B.A., Yamagata, D.K., Kurosaka, M., Yamawaki, S. and Maya, T. (1997) Anti-Kidney Pair of Vortices in Shaped Holes and Their Influence on Film Cooling Effectiveness. ASME Paper 97-GT-45. http://dx.doi.org/10.1115/97-gt-045
- 15. Walters, D.K. and Leylek, J.H. (2000) A Detailed Analysis of Film Cooling Physics: Part 1-Streamwise Injection with Cylindrical Holes. ASME Journal of Turbomachinery, 122, 102-112. http://dx.doi.org/10.1115/1.555433
- 16. Leylek, J.H. and Zerkle, R.D. (1994) Discrete-Jet Film Cooling: A Comparison of Computations Results with Experiments. ASME Journal of Turbomachinery, 116, 358-368. http://dx.doi.org/10.1115/1.2929422
Nomenclature
a: spacing between main hole and side hole centerlines
b: streamwise offset between main hole and side hole centerlines
AVH: anti-vortex hole
CFD: computational fluid dynamics
CFL: Courant-Friedrichs-Lewy (CFL) condition
CRV: counter-rotating vortex
dm: main hole diameter
ds: side hole diameter
DR: density ratio―density of coolant/density of freestream―
k-ω: k-omega turbulence model
M: blowing ratio―mass flux of coolant/mass flux of freestream―
P: spanwise angle of side hole
p: static pressure at outlet
p0: total pressure at inlet
Q: streamwise pitch angle of side hole
R: angle between main hole and side hole
RANS: Reynolds Averaged Navier-Stokes
Tin: inlet temperature
Tfilm: local temperature affected by film cooling
Tc: coolant temperature
Tu: turbulence intensity
u*: friction velocity at the nearest wall
URANS: unsteady Reynolds averaged Navier-Stokes
V: velocity
x: streamwise distance
y: spanwise distance
y+: non-dimensional wall distance―u*y/ν
z: vertical distance (cross stream)
Greek Variables
ηaw: film cooling effectiveness
ϴ: dimensionless temperature―
Lx: turbulence length scale
ν: kinematic viscosity
ρ: coolant density
ρin: freestream density






















