Journal of Flow Control, Measurement & Visualization
Vol.2 No.3(2014), Article ID:48091,11 pages
DOI:10.4236/jfcmv.2014.23011
Unsteady Behavior of Cavitating Waterjet in an Axisymmetric Convergent-Divergent Nozzle: High Speed Observation and Image Analysis Based on Frame Difference Method
Shota Hayashi, Keiichi Sato
Department of Mechanical Engineering, Kanazawa Institute of Technology, Nonoichi, Japan
Email: ksato@neptune.kanazawa-it.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 January 2014; revised 14 March 2014; accepted 21 April 2014
ABSTRACT
Although it is well known that cloud cavitation shows unsteady behavior with the growing motion of an attached cavity, the shedding motion of a cloud, the collapsing motion of the cloud shed downstream and a reentrant motion in flow fields such as on a 2-D hydrofoil and in a convergentdivergent channel with a rectangular cross-section, observations for the periodic behavior of cloud cavitation in a cylindrical nozzle with a convergent-divergent part, which is mainly used in an industrial field, have hardly been conducted. From engineering viewpoints, it is important to elucidate the mechanism of periodic cavitation behavior in a cylindrical nozzle. In this study, a high-speed observation technique with an image analysis technique was applied to the cloud cavitation behavior in the nozzle to make clear the mechanism of unsteady behavior. As a result, it was observed in the nozzle that the periodic behavior occurs in the cloud cavitation and pressure waves form at the collapse of clouds shed downstream. Also, it was found through the image analysis based on the present technique that the pressure wave plays a role as a trigger mechanism to cause a reentrant motion at the downstream end of an attached cavity.
Keywords: Cloud Cavitation, Cylindrical Convergent-Divergent Nozzle, High Speed Observation, Image
Analysis

1. Introduction
It is well known that unsteady cloud cavitation shows a periodic behavior with the growing motion of an attached cavity, the shedding motion of a cloud, the collapsing motion of the cloud shed downstream and a reentrant motion in flow fields such as on a 2-D hydrofoil and in a convergent-divergent channel with a rectangular cross-section [1] -[5] . Also, there is a highly-intensive impact caused by the collapse of shed clouds [6] and the cloud cavitation is considered to be a self-oscillation phenomenon based on the reentrant motion instability related to an attached cavity length and the adverse pressure gradient at the reattachment zone of separated cavity [7] [8] . It has also been found that the reentrant motion that moves along the surface of a hydrofoil or the divergent part of a nozzle within an attached cavity toward the leading edge is closely related to the mechanism of the shedding motion in cloud cavitation [9] [10] . Kawanami et al. [11] reported that an obstacle was installed on a hydrofoil surface to stop the reentrant motion from flowing toward its leading edge and obtained the result on the suppression of a large cloud shedding and the reduction of cavitation noise. However, some researchers suggested that there can be other mechanisms for the reentrant motion, such as existence of a condensation shock [12] and a collapse of cloud with a shock wave [13] . Thus the cause of the reentrant motion has yet to be completely elucidated.
There are still some unsolved points about the mechanism of the periodic cloud cavitation behavior, which are, for example, whether the reentrant motion can be considered to be mainly composed of liquid flow or accompanied with pressure waves and how it is caused in a separated cavity flow [3] . From engineering viewpoints such as the design of a water jet nozzle suitable for washing and cutting as well as a diesel injector nozzle for atomizing [14] , it is important to make clear the mechanism of periodic cavitation behavior to apply the high-intensive impact and the mixing action through the controlling of cavitation clouds.
Thus, the authors, so far, have experimentally studied about the cloud cavitation behavior in a convergentdivergent channel with a rectangular cross-section from a viewpoint of a two-dimensional plane flow. As a result, it has been demonstrated [2] [3] [15] that 1) the reentrant motion can be triggered by the pressure wave propagation which is caused through the collapse of the cloud shed downstream, 2) it moves toward the throat of the convergent-divergent nozzle through the local collapses of microscopic bubble clusters, accompanied with the formation and the propagation of pressure waves in an attached cavity [3] , 3) a local intrusion due to the chainreaction collapses of bubble clusters at the nozzle throat produces a suppressive action on the supply of upstream vorticities, and 4) the attached cavity broken off at the nozzle throat is shed downstream as a large vortex structure after the coalescence of small cavitation vortices.
On the other hand, cylindrical convergent-divergent nozzles are widely used in an industrial field such as a water jet nozzle and a diesel injector nozzle. From an axisymmetric flow viewpoint, however, detailed studies and observations have hardly been conducted about a periodic behavior and a reentrant motion mechanism in unsteady cloud cavitation. In the present study, a high-speed observation technique and an image analysis based on a frame difference method were applied to analyze and estimate an unsteady behavior of cloud cavitation in a cylindrical convergent-divergent nozzle. The present analysis method and the experimental data can greatly contribute to the research for complicated unsteady behaviors of cloud cavitation in a separated flow and in a convergent-divergent nozzle.
2. Experimental Facilities and Methods
2.1. Water Jet Test Apparatus
Figure 1 shows the schematic of water jet apparatus used in the experiment. Using a high-pressure pump with 3 plungers, tap water was jetted from a submerged nozzle into a large water tank. There are observation windows on the sides of the tank. The pump operated at a discharge pressure of 30 MPaG, a flow rate of 33 L/min and a rotational speed of 340 rpm. The conditions at the test section were set through a control valve system. The water level in the tank was kept at constant height by overflowing to a storage tank. A pressure transducer (JTEKT, PMS-8M-2) and an electromagnetic flow meter (KEYENCE, FD-M100AY) were installed on the upstream part of the nozzle, and the voltage waveforms corresponding to pressure were recorded through an amplifier (JTEKT, AA6210), logged by a data logger (KEYENCE, NR-350) at 25 kHz of sampling frequency and monitored on PC. After data were obtained, the frequency range higher than 1 kHz was removed out by a digital low-pass filter. Since a plunger pump was used in the present study, there were some pressure fluctuations at the upstream part of the nozzle. Figure 2 shows fluctuating pressure upstream of the nozzle obtained with the pressure transducer. The attached cavity in the nozzle increases in length as the upstream pressure is higher and decreases in length as the pressure is lower. The upstream pressure fluctuates at frequency of about 17 Hz which corresponds to the

Figure 1. Schematic of experimental facilities.
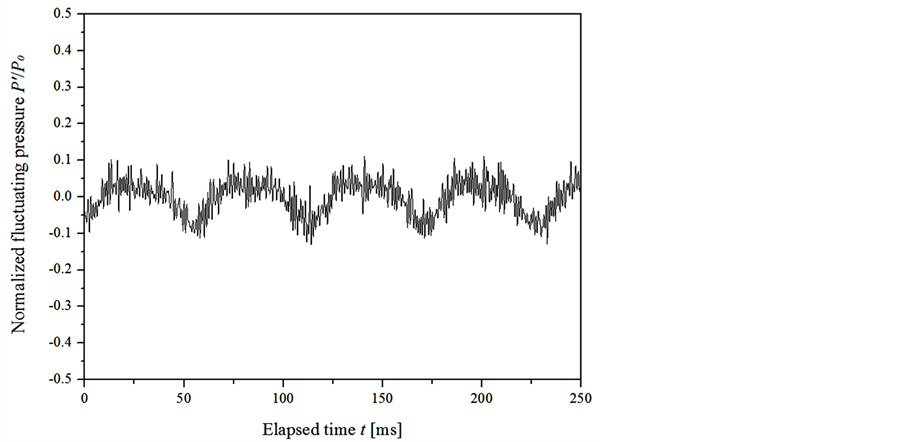
Figure 2. Fluctuating upstream pressure.
rotational speed of the pump with 3 plungers. It is also found that there are different fine waves with a higher frequency. According to the previous results by Sato et al. [16] , it should be noted that there are two kinds of pressure waveforms in the present cavitating nozzle flow and the upstream pressure fluctuating at the lower frequency component is not related to the periodic cavity behavior with higher frequency component, which is typically found in periodical cloud cavitation and peculiar to it.
A high-speed video camera was used to observe the periodic behavior of cloud cavitation in the cylindrical convergent-divergent nozzle. The high-speed video camera (Photron, FASTCAM SA5, image size of 536 × 64 or 376 × 128 pixels at 100,000 fps) was set up near the transparent side wall of the large tank. A plane light guide connected to a 350 W metal halide lamp with continuous light (NPI, PCS-UMX 350) was installed in the tank at the opposite side of the camera across the nozzle. The camera was synchronized with the pressure transducer.
Reynolds number at the throat of the nozzle was calculated as follow,
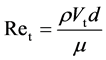 (1)
(1)
where ρ is density of water, Vt velocity in the throat of a cylindrical convergent-divergent nozzle, d the inside diameter of the nozzle and μ viscosity of water. Also, both cavitation numbers at the upstream part and the throat of the nozzle were calculated respectively as follows.
 (2)
(2)
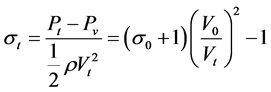 (3)
(3)
In equations (2) and (3), P0 is upstream pressure, Pv vapor pressure of water, V0 upstream velocity and Pt pressure at the nozzle throat, respectively. Equation (3) was based on the Bernoulli’s equation under the assumption that there was no pressure loss between the upstream and the throat part.
2.2. Cylindrical Convergent-Divergent Nozzle
Figure 3 shows a cylindrical convergent-divergent nozzle used in the present study. The nozzle is made of transparent acrylic resin. It has a convergent angle of 90 degree and a divergent angle of 20 degree. D and d are 8 mm and 4 mm in diameter, respectively. In addition, its flat and smooth outer surface with high transparency allows for obtaining clear images through an optical observation. The position of the nozzle throat is chosen as origin, and the flow direction from the origin is defined as x-axis. In experimental results, distance x is normalized by the throat diameter d.
3. Image Analysis Method
A frame difference method [17] -[19] is used to analyze the images obtained from a high-speed video observation, in which a gray level technique is applied, as shown in Figure 4. This method allows us to analyze and estimate the periodic behavior of cloud cavitation in various cavitating flow fields such as in a convergent-divergent test section [3] and a high-speed water jet [18] [19] .
The images obtained by the high-speed video camera have 256 gray levels (8 bit grayscale images are used). First, images are taken out from a recorded video. Then an analysis region with m × n pixels as shown in Figure 4(a) is set, in which gray levels are averaged in a width direction normal to the flow direction. Hence, the averaged gray level in a width direction or in row i on a m × n pixel analysis region Gai is calculated as follows,
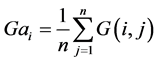 (4)
(4)
where G(i, j) is the gray level at a cell (i, j). As shown in Figure 4(b), for example, one-dimensional gray level distributions in the x-direction are obtained over all the images. Second, the difference values of the averaged gray level Gai are calculated every time interval over a range of the whole time as shown in Figure 4(c).
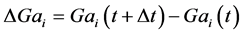 (5)
(5)
Here, in the present case, Δt is 1 × 10−5 s because of the frame rate 100,000 fps. The cloud area is in darker color than the color of a background. Subtracting the colors in the image at t from those of t + Δt, the negative difference values (ΔGai < 0) indicate the appearance of cavities (or clouds, bubbles) and the positive values (ΔGai > 0) indicate the disappearance of them. Next, the difference values of gray level Gai are colored again, based on the definition of gray level transformation (with N = 6 in the present study) as shown in Figure 4(d), and then the same procedure is applied to all the difference values, where N will be discussed later. Finally, the newly-colored difference values are ordered in time to obtain the contour map of the difference values based on the averaged gray levels, which shows the relationship between normalized distance x/d and elapsed time t, as shown in Figure 4(e). In the contour map, white regions show the appearance of cavities and black regions show the disappearance of them as mentioned just before.
Using the transformation curve shown in Figure 4(d), the gray level area above the maximum value divided by N = 6 is colored with black and the area below the minimum value divided by 6 is colored with white. There are 21 gray shades between the values. Figure 5 shows the contour maps in various values of N. We can effectively reflect small changes in the frame difference values using an appropriate choice of N or the slope of the transformation curve. It should be noted that our attention is focused on the boundary of the appearance or dis-

Figure 3. Cylindrical convergent-divergent nozzle.

Figure 4. Outline of image analysis method. (a) Schematic of obtained image; (b) Gray level distribution; (c) Difference of gray level; (d) Definition of gray level transformation; (e) Contour map.
appearance of cavitation clouds. In the present range of the images and the image analysis, we chose N = 6 as the transformation value because it was found that the contrast of the contour map is more enhanced with increasing the value of N and becomes a little obscure in the darker colors around N = 8.
 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 5. Image analysis results for various values of N. (a) N = 1; (b) N = 4; (c) N = 6; (d) N = 8.
4. Experimental Results
4.1. Observation for Unsteady Behavior of Cloud Cavitation
Figure 6 shows typical successive images on the behavior of cloud cavitation in the present experiment. A flow direction is from the top to the bottom in the images. Black regions in the images show an attached cavity region, shedding cavitation clouds and/or cavitation bubbles, except for nozzle contour lines. As indicated by arrows A in Figure 6, a shedding cloud moves downstream, then collapses at about t = 5.63 ms and a few rebounds of the cloud occur repeatedly until the final disappearance, where we can find many residual small bubbles in the downstream area. As the shed cloud moves downstream, an attached cavity grows and extends downstream as indicated by arrows B. Just after the main collapse around t = 5.63 ms, a reentrant motion (arrows C) starts and moves upstream along the divergent wall of the nozzle toward the nozzle throat. Around t = 6.43 ms the reentrant motion reaches the nozzle throat and a new attached cavity begins to grow as shown in arrows E, where we can find the existence of small-scale ring-like vortex cavities in the region downstream of the throat around t = 6.33 - 6.53 ms. At this stage, a large-scale attached cavity appears to be totally separated from the nozzle throat by the reentrant motion, moves downstream through the coalescence of the vortex cavities and shed downstream as a new large cloud with large-vortex structure indicated by arrows D where the growth of cloud is followed by the arrows A since this process is repeated in the similar pattern. At the same time that the reentrant motion reaches the nozzle throat, the following attached cavity (arrows E) starts growing and moving on to the following cycle.
4.2. Image Analysis Results for Unsteady Behavior of Cloud Cavitation
Figure 7 shows typical results of the image analysis based on the frame difference method explained in the last Section 3. Figure 6 and Figure 7 are associated with each other. Each of the phenomena indicated by the alphabetic characters A-E in Figure 7 corresponds to the phenomenon indicated by the same English characters in Figure 6, respectively. In the image analysis results, white regions indicate the appearance of bubbles, cavities and clouds, while black regions indicate the disappearance of them. In Figure 7(a), a cloud is shed downstream as indicated by white line-like zones A and D, while an attached cavity grows downstream from the nozzle throat as shown in white line-like zones B and E. On the other hand, the black line-like zone C shows a reentrant motion from the downstream part to the nozzle throat.
In Figure 7(a), there is a clear black vertical line around t = 5.6 ms and x/d = 6.0 as indicated by a mark “Collapse”. Around this area, a large shedding cloud collapses heavily as shown in the image at t = 5.63 ms in Figure 6. The black vertical line means the trace of the pressure wave propagation [19] because a continuous collapse of microscopic bubbles is caused at the arrival of high pressure wave in the surrounding area of the strong cloud collapse. The black line is nearly perpendicular to the time axis in Figure 7(a), which means that the propagation has very fast speed.
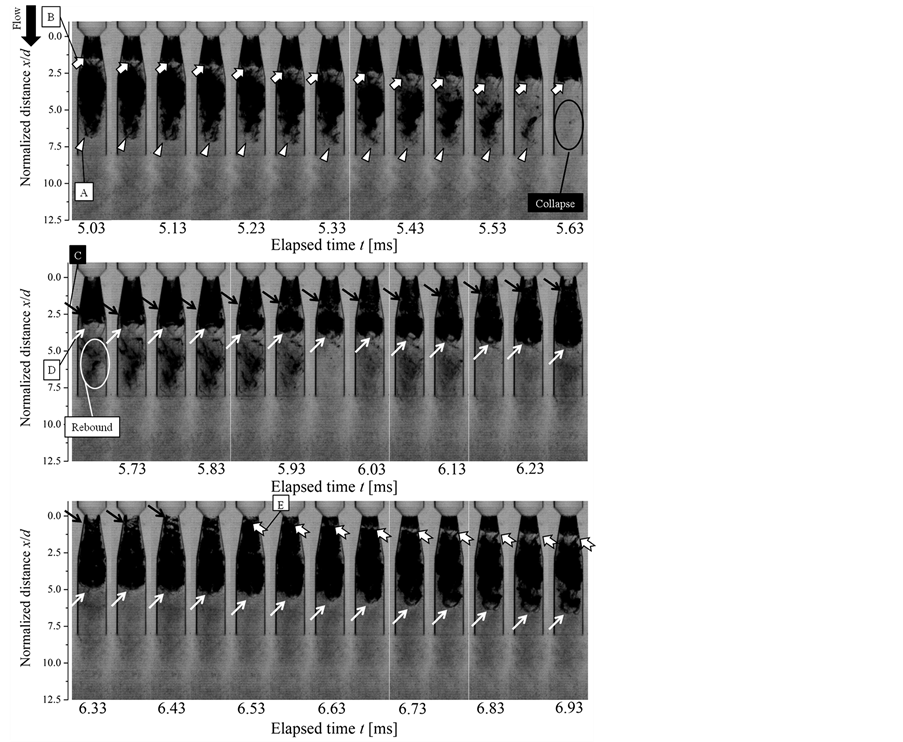

Figure 6. Observation for unsteady behavior of cloud cavitation. Fs = 100,000 fps, Tw = 291 K, P0 = 0.20 MPaG, V0 = 4.3 m/s, Ret = 6.9 × 104, σt = 1.1.
From the slope of the black lines as shown in an enlarged image in Figure 7(b), it turns out that the speed of the pressure wave propagating downstream at the collapse is about 650 m/s and that of the wave propagating upstream is about 400 m/s. Here, it should be noted that the propagation speeds estimated from the slope of lines have some uncertainty because of low space resolution in the image analysis. The wave propagation speed at the value of 400 or 650 m/s is compared with the speed in a gas-liquid two phase flow [20] . Figure 7(c) shows the detailed still pictures in the region near the collapse shown in Figure 7(b). For example, from the viewpoint of the movement propagating upward from the collapse the pictures can be shown as follows. First, the bubble indicated by (f) reaches a small size within the pictures around t = 5.61 ms, when the local cloud area (h) is dark and the bubble (g) is relatively large. Next, at t = 5.62 ms the bubble (f) becomes larger slightly, the color of the cloud area (h) and the size of the bubble (g) tend to decrease, and the string-like bubble (i) in the upper part of the picture is still large. At t = 5.63 ms the bubble (g) almost collapses and the bubble (i) is also disappearing. At t = 5.64 ms the rebound phenomenon is observed in the area (h). The collapsing behavior is in agreement with the upward propagation indicated by Figure 7(b). The result confirms the effectiveness of the present image

Figure 7. Image analysis for unsteady behavior of cloud cavitation (analysis region of 311 × 48 pixels is set and this image analysis result and the successive images in Figure 6 are associated with each other). Fs = 100,000 fps, Tw = 291 K, P0 = 0.20 MPaG, V0 = 4.3 m/s, Ret = 6.9 × 104, σt = 1.1.
analysis method. More details have been shown about the image analysis results and the pressure wave propagation in the cavitating area by Sato et al. (e.g. [19] ).
After the main collapse, a few rebounds of the cloud occur because several black and white lines are observed repeatedly, corresponding to the appearance and disappearance of microbubbles in the flow field as also shown in Figure 6.
From Figure 7(a) and Figure 7(b), it is also found that a reentrant motion (zone C) starts moving upstream toward the throat along the divergent wall of the nozzle at the same time that the pressure wave reaches the growing motion of attached cavity as indicated by point “p”. This fact means that the arrival of the pressure wave plays a role on a trigger for the reentrant motion. The resulting reentrant motion can be estimated about 13.4 m/s ± 1.2 m/s from the slope of the line C (zone C).
When the reentrant motion denoted by C reaches the nozzle throat around t = 6.5 ms, the following attached cavity starts growing as shown in the region E in a similar manner to the previous region B-D. The line-like regions B-D and E appears to be white because the attached cavity shows a growing and appearance motion. The growing speed can be estimated about 10.6 m/s ± 0.3 m/s from the slope of the line E (zone E). The velocity of the reentrant motion is estimated about Vj = 13.4 m/s ± 1.2 m/s from the slope of the line C as just mentioned before. The velocity Vs at an attached cavity surface, on the other hand, was approximated by Jakobsen [12] based on the Bernoulli’s theorem as follow,
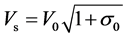 (6)
(6)
where V0 is upstream velocity. In the present study, the velocity at
the cavity surface was estimated Vs = about 24.8 m/s. Hence,
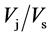 is approximately 0.54. This value almost agrees
with that by Callenaere et al. [21] who reported
that the velocity of the reentrant jet moving in an attached cavity was approximately
a half of that in the main stream for sheet cavitation in a Venturi-type test section.
is approximately 0.54. This value almost agrees
with that by Callenaere et al. [21] who reported
that the velocity of the reentrant jet moving in an attached cavity was approximately
a half of that in the main stream for sheet cavitation in a Venturi-type test section.
As shown in Figure 6 and Figure 7, after the reentrant motion denoted by C reaches the nozzle throat, a new attached cavity forms and grows downstream with the progress of time (zone E). The existing vortex cavities move downstream as a cavitation cloud coalescing with each other. In Figure 7, since the leading end of the shedding cloud corresponds to the white line-like zone D as mentioned above, the shedding cloud exists between the white lines D and E in a given time t. Here, it is interesting that the reentrant motion C switches to the formation of an attached cavity E around the nozzle throat.
Figure 8 shows the typical image analysis result and the successive images based on the high-speed video
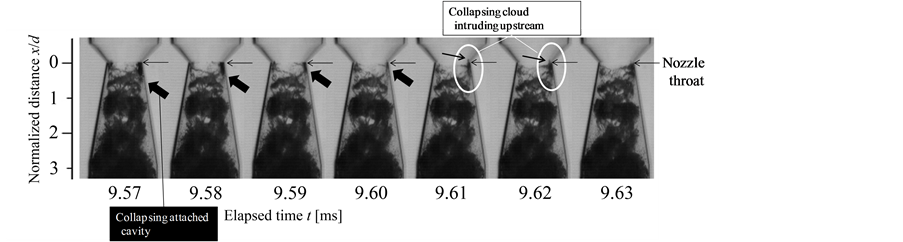
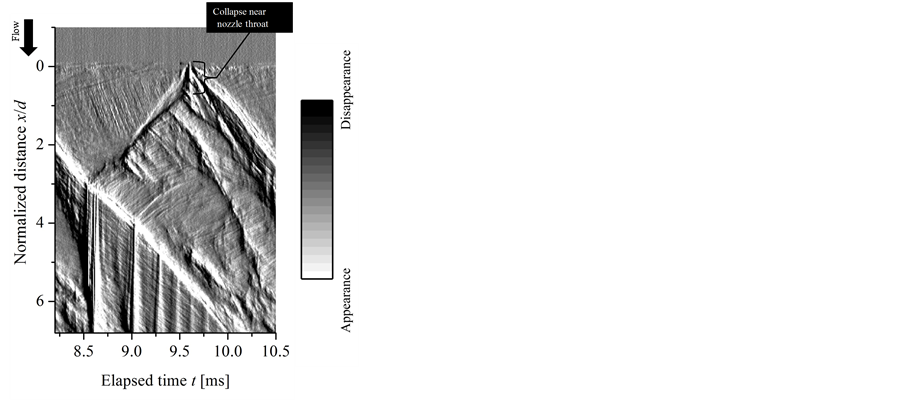
Figure 8. Image analysis for detailed observation near nozzle throat (analysis region of 375 × 41 pixels is set). Fs = 100,000 fps, Tw = 293 K, P0 = 0.20 MPaG, V0 = 4.3 m/s, Ret = 7.0 × 104, σt = 1.1.
observation for the behavior of cavities near the nozzle throat around the switching
period from the reentrant motion to the formation of the attached cavity. A characteristic
result in the image analysis appears as a nearly vertical black line in the vicinity
of the nozzle throat where the black line extends above the nozzle throat . From the results, it is pointed out
that relatively-strong collapses of the bubble clusters occur in the vicinity of
the nozzle throat and affect the flow from the upstream at that moment. A new attached
cavity starts forming and growing, just after the collapsing behavior of the babble
clusters.
. From the results, it is pointed out
that relatively-strong collapses of the bubble clusters occur in the vicinity of
the nozzle throat and affect the flow from the upstream at that moment. A new attached
cavity starts forming and growing, just after the collapsing behavior of the babble
clusters.
5. Concluding Remarks
The periodic behavior of cloud cavitation was observed in a cylindrical convergent-divergent nozzle using a high-speed observation technique and an image analysis based on a frame difference method. The main results are experimentally obtained through the high-speed observation as follows.
1) The frame difference method presented in this investigation is most effective to analyze and estimate the unsteady behavior of cloud cavitation.
2) At the collapse of cavitation cloud shed downstream, pressure waves form and propagate toward the surrounding area.
3) The pressure wave propagating upstream at the collapse of the cloud is considered to be a trigger mechanism to cause the reentrant motion from the downstream end of an attached cavity.
4) The reentrant motion moves within an attached cavity formed from the nozzle throat at about a half of the flow speed on the cavity surface.
5) The local collapse of bubble clusters is observed in the vicinity of the nozzle throat. The collapse affects an upstream flow and begins to form a new attached cavity at the same time that the attached cavity becomes broken off and a large cavitation cloud begins to form with vortex structure.
Acknowledgements
The authors would like to thank Dr. Yasuhiro Sugimoto and Dr. Kazuki Niiyama for their kind and helpful advice on this study.
References
- Furness, R.A. and Hutton, S.P. (1975) Experimental and Theoretical Studies of Two-Dimensional Fixed-Type Cavities. Journal of Fluids Engineering, 97, 515-521. http://dx.doi.org/10.1115/1.3448098
- Sato, K., Saito, Y. and Nakamura, H. (2001) Self-Exciting Behavior of Cloud-Like Cavitation and Micro-Vortex Cavities on the Shear Layer. Proceedings of the 1st Symposium on Advanced Fluid Information, Sendai, 4-5 October 2001, 263-268.
- Sato, K., Wada, Y., Noto, Y. and Sugimoto, Y. (2010) Reentrant Motion in Cloud Cavitation due to Cloud Collapse and Pressure Wave Propagation. Proceedings of ASME 2010 3rd Joint US-European Fluids Summer Meeting, Montreal, 1-5 August 2010, 7-11. http://dx.doi.org/10.1115/FEDSM-ICNMM2010-30350
- Franc, J.P. and Michel, J.M. (2004) Fundamentals of Cavitation. Kluwer Academic Publishers, Dordrecht.
- Kjeldsen, M., Arndt, R.E.A. and Effertz, M. (2000) Spectral Characteristics of Sheet/Cloud Cavitation. Journal of Fluids Engineering, 122, 481-487. http://dx.doi.org/10.1115/1.1287854
- Reisman, G.E., Wang, Y.C. and Brennen, C.E. (1998) Observation of Shock Waves in Cloud Cavitation. Journal of Fluid Mechanics, 355, 255-283. http://dx.doi.org/10.1017/S0022112097007830
- Le, Q., Franc, J.P. and Michel, J.M. (1993) Partial Cavities: Global Behavior and Mean Pressure Distribution. Journal of Fluids Engineering, 115, 243-248. http://dx.doi.org/10.1115/1.2910131
- Callenaere, M., Franc, J.P., Michel, J.M. and Riondet, M. (2001) The Cavitation Instability Induced by the Development of a Re-Entrant Jet. Journal of Fluid Mechanics, 444, 223-256. http://dx.doi.org/10.1017/S0022112001005420
- Sakoda, M., Yakushiji, R., Maeda, M. and Yamaguchi, H. (2001) Mechanism of Cloud Cavitation Generation on a 2-D Hydrofoil. Proceedings of the 4th International Symposium on Cavitation, Pasadena, 20-23 June 2001, 1-8.
- Knapp, R.T. (1955) Recent Investigations of the Mechanics of Cavitation and Cavitation Damage. Transactions of ASME, 77, 1045-1054.
- Kawanami, Y., Kato, H., Yamaguchi, H., Tanimura, M. and Tagaya, Y. (1997) Mechanism and Control of Cloud Cavitation. Journal of Fluids Engineering, 119, 788-794. http://dx.doi.org/10.1115/1.2819499
- Jakobsen, J.K. (1964) On the Mechanism of Head Breakdown in Cavitating Inducers. Journal of Basic Engineering, 86, 291-305. http://dx.doi.org/10.1115/1.3653066
- Leroux, J.-B., Astolfi, J.A., Billard, J.Y. (2004) An Experimental Study of Unsteady Partial Cavitation. Journal of Fluids Engineering, 126, 94-101. http://dx.doi.org/10.1115/1.1627835
- Stanley, C., Barber, T., Milton, B. and Rosengarten, G. (2011) Periodic Cavitation Shedding in a Cylindrical Orifice. Experiments in Fluids, 51, 1189-1200. http://dx.doi.org/10.1007/s00348-011-1138-7
- Sato, K. and Shimojo, S. (2003) Detailed Observations on a Starting Mechanism for Shedding of Cavitation Cloud. Proceedings of the 5th International Symposium on Cavitation, Osaka, 1-4 November 2003, 1-7.
- Sato, K., Taguchi, Y. and Hayashi, S. (2013) High Speed Observation of Periodic Cavity Behavior in a ConvergentDivergent Nozzle for Cavitating Water Jet. Journal of Flow Control, Measurement & Visualization, 1, 102-107. http://dx.doi.org/10.4236/jfcmv.2013.13013
- Sugimoto, Y., Sato, K. and Oojimi, S. (2008) Visualization of Pressure Wave Generated by Collapse of Cavitation Cloud Using Frame Difference Method. Proceedings of the 13th International Symposium on Flow Visualization/the 12th French Congress on Visualization in Fluid Mechanics, Nice, 1-4 July 2008, 497-506.
- Sato, K., Kaida, N. and Sugimoto, Y. (2012) Collapses of Cavitation Cloud and Pressure Wave Propagation in Cavitating Water Jet Obliquely Impinging on Solid Wall. Proceedings of the 8th International Symposium on Cavitation, Singapore, 13-16 August 2012, 305-310. http://dx.doi.org/10.3850/978-981-07-2826-7_064
- Sato, K., Sugimoto, Y. and Ohjimi, S. (2009) Pressure-Wave Formation and Collapses of Cavitation Clouds Impinging on Solid Wall in a Submerged Water Jet. Proceedings of the 7th International Symposium on Cavitation, Ann Arbor, 17-22 August 2009, 1074-1085.
- Brennen, C.E. (1995) Cavitation and Bubble Dynamics. Oxford University Press, Oxford.
- Callenaere, M., Franc, J.P. and Michel, J.M. (1998) Influence of Cavity Thickness and Pressure Gradient on the Unsteady Behavior of Partial Cavities. Proceedings of the 3rd International Symposium on Cavitation, Grenoble, 7-10 April 1998, 209-214.
Nomenclature
D: Inside diameter of upstream part of nozzle d: Inside diameter of nozzle throat Fs: Frame speed G(i, j): Gray level at cell (i, j)
Ga: Average gray level m: Number of image pixels in height direction N: Numerical value dividing maximum and minimum difference values n: Number of image pixels in width direction P’: Upstream fluctuating pressure P0: Average upstream pressure Pv: Vapor pressure of water Pt: Pressure at nozzle throat Ret: Reynolds number at nozzle throat t: Elapsed time Tw: Water temperature Vt: Velocity at nozzle throat V0: Upstream velocity Vs: Velocity at surface of attached cavity Vj: Velocity of reentrant motion x: Distance from nozzle throat
μ: Viscosity of water
ρ: Density of water
σ0: Upstream cavitation number
σt: Cavitation number at nozzle throat

