Open Journal of Earthquake Research
Vol.04 No.03(2015), Article ID:58723,7 pages
10.4236/ojer.2015.43009
Application of Omori’s Decay Law to the 2001 Bhuj Aftershock Sequence for Kachchh Region of Western India
Parul C. Trivedi
India Meteorological Department, Ahmedabad, India
Email: pctrivedi123@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 June 2015; accepted 8 August 2015; published 11 August 2015
ABSTRACT
In the present study, the temporal behavior of 2001 Bhuj aftershock sequence in Kachchh region of western peninsular India is studied by the modified Omori law. The Omori law parameters p, c and K are determined with the standard errors by the maximum likelihood estimates using ZMAP algorithm in MatLab environment. The entire aftershock sequence is analyzed by diving it into three separate series with respect to time to weigh up the bigger earthquake of magnitude M 5.7 occurring on March 7, 2006 at Gedi fault. This study helps to understand the cumulative effect of the aftershocks generated by this bigger earthquake of the mainshock sequence. The results of this analysis are discussed with other studies of the different earthquake sequence for the different parts of the world and suggest that all the three series of Bhuj aftershock sequence follow the Omori relation. Values of parameter p vary significantly from series 1 to series 3, i.e., p-value varies significantly with time. Similarly, other two Omori law parameters K and c are also found to change significantly with time. These parameters are useful to describe temporal behavior of aftershocks and to forecast aftershock activity in time domain. Aftershock decay rate provides insight into stress release processes after the mainshock, thus helping to understand the heterogeneity of the fault zone properties and evaluate time-dependent seismic hazard analysis over the region.
Keywords:
Omori Decay Law, Aftershock Activity, p-Value, Bhuj Earthquake

1. Introduction
Earthquakes are the deadliest natural hazards amongst all other natural hazards that cause lots of casualties and damage of property. Kachchh region of western India is one of the most earthquake prone zones of the world and witnessed three large earthquakes including 2001 Bhuj earthquake of Mw 7.7 at the beginning of the 21st century. Many researchers have studied this devastation earthquake and its impact by different approaches [1] -[5] .
In earthquake physics, the magnitude distribution of Gutenberg-Richter relationship reflects fundamental properties of how earthquakes grow and stop and the time-dependence of earthquake occurrence in strict way is generally ignored in standard seismic hazard assessment, though the time-dependent earthquake clustering is well known. In seismological studies, the Omori law, proposed by Omori in 1894 is one of the basic empirical laws [6] which is well established in seismology and describes the rate of decay of aftershocks with time following the mainshock. This law describes how aftershock activity will decay with time. Omori’s law and its modified forms have been used widely as a fundamental tool to study aftershock activity with respect to time. An extension of the modified Omori’s law is the Epidemic Type of Aftershock Sequences (ETAS) model. It is a stochastic version of the modified Omori law. In the ETAS model, the rate of aftershock occurrence is an effect of combined tests of all secondary aftershock subsequences produced by each aftershock. It is observed that seismicity maps for many regions are dominated by aftershock activity. Most of aftershocks are too small to cause damage but following a large mainshock one or more may be powerful enough to cause additional damage and casualties. We have the example of California earthquake; after the occurrence of 1994 M 6.7 Northridge, California, earthquake, more than 3000 aftershocks were recorded during the first few weeks. For the same sequence, one aftershock of magnitude 5.2 caused $7 million damage just to handle electric utility equipments. When we look back to Reid’s elastic rebound theory, the basic physical process involved in the generation of earthquake is slow building up and rapid release tectonic stress in a cyclic process. This theory also provides insight into aftershock activity after the occurrence of a large earthquake. Thus the study of aftershocks and the pattern in which they grow is very important and essential for seismic hazard analysis. Many researchers have studied the aftershock sequence for different regions since the formulation of Omori’s law in 1894: continental transforming fault zones by Kisslinger and Jones (1991), continental collision zones by Pavlis and Hamburger (1991) and subduction zone environments by Bohnenstiehl et al. (2002) [7] - [9] . Utsu et al. (1995) reviewed statistical aspects of the Omori law and summarized a large number of studies of aftershock sequences [10] .
In the present study, the aftershock sequence of 2001 Bhuj earthquake of Mw 7.7 for Kachchh region of western peninsular India is studied by the modified Omori law. The entire aftershock sequence from January 26, 2001 to the December 31, 2014 is categorized in three series and parameter p along with c and K is determined for all three series. As stated earlier, many researchers have addressed the 2001 Bhuj earthquake (Mw 7.7) with different scientific approaches but the aftershock activity over the Kachchh region is less attended. Here, an attempt is made to examine Omori’s decay law for long ongoing aftershock sequence of 2001 Bhuj earthquake (Mw 7.7). The results presented in this study are very useful to understand temporal behavior of aftershocks and to forecast aftershock activity in the future. It has significant implications on seismic hazard analysis since the study gives idea on stress release processes after the mainshock.
2. Data and Method
In the present study, the Omori’s law is tested against earthquake catalogs for the aftershock sequences of the January 26, 2001 Bhuj earthquake. Catalogue of India Meteorological Department (IMD) and Institute of Seismological Research (ISR) are used and verified with catalogue of International Seismic Centre (ISC), United States Geological Survey (USGS) and Geological Survey of India (GSI). In this study, the aftershocks from next hour of large earthquake on January 26, 2001; 08:46 hours local time to December 31, 2014; 24:00 hours local time with magnitude of M ≥ 1.5 are used. Most importantly, records of digital seismographs installed immediately after the mainshock by India Meteorological Department (IMD) near mainshock epicenter and adjoining area within Kachchh region are used extensively in this study. Afterwards, on the establishment of ISR seismological observatories, earthquake data recorded by the ISR network is included to weigh lower magnitude aftershocks and to achieve high quality completeness of catalogue. Total 11,334 aftershocks of M ≥ 1.5 are used in the study. A general observation regarding the Omori law decay parameter shows no correlation with cutoff magnitude. Initially, three different calculations performed on the basis of diurnal, weekly and monthly distribution of events as the period immediate after the mainshock is considered the most intense period of seismic activity. Later on month wise and year wise frequency of aftershocks is analyzed. It is important to note, however, that the main shock of larger size of Mw 7.7 is expected to produce aftershocks for years, even decades and sometimes an aftershock produced at any time may be large as each aftershock in turn that generates its own aftershocks which we can call secondary aftershocks and thus the long-term aftershock risk should be specially emphasized.
The Omori law (1894) states that the main earthquake is immediately followed by a sequence of aftershocks whose frequency of occurrence decays at the rate proportional to t−p, where p ~ 1. The simplest version of Omori’s Law can be written as,
 (1)
(1)
However, in most of scientific studies, more commonly, a modified version of this law is used. In fact, it resembles more closely the original, empirically-derived model developed by Omori in the 1890s [6] [11] . This modified Omori law describes the rate of decay of an aftershock sequence by equating the number of aftershocks N at some time t after the mainshock including three other constants.
The modified version of Omori can be given as follow:
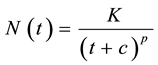 (2)
(2)
 (3)
(3)
In this equation, N is the number of events following the mainshock, dN/dt is the occurrence rate of aftershocks with magnitudes greater than a lower cutoff Mc, t is time since a mainshock while, K, c and p are empirical constants. Shcherbakov et al. (2004) proposed a generalized Omori’s law for aftershocks combining Gutenberg-Richter b-value [12] and Omori’s p-value and gave the rate of occurrence of aftershocks with magnitude greater than Mgiven as a function of time t, b-value, mainshock magnitude Mmainshock and the difference of mainshock-maximum aftershock magnitude Δm as follow,
 (4)
(4)
Of the Omori law parameters, we can immediately observe that K may be related to aftershock productivity, c to the period of time after the mainshock during which the aftershock rate is roughly constant and p to the power law decay in the rate of aftershocks. This is helpful when it is necessary to calculate the number of aftershocks in a given time interval from the Omori law. The significance of equation 2 and equation 3 is the constant that defines the rate of decay i.e., the p-value by graphing a simple model of Omori’s Law. This allows us to see how the shape of an exponential decay curve looks like and how the shape changes with the value of p―the rate of decay. Actually, c is no longer a constant but scales with a lower magnitude cutoff and a mainshock magnitude. In this study, the entire aftershock sequence is divided into three series. First series, initial aftershocks from next hour to 365 days i.e. from January 26, 2001 to January 25, 2002; second series is from January 26, 2001 to March 7, 2006 up to the occurrence of earthquake of M 5.7; the maximum magnitude aftershock of the entire sequence which in turn again generated aftershocks of its own and finally for the entire aftershock sequence i.e. January 26, 2001 to December 31, 2014. The parameters in the modified Omori formula are estimated accurately by the maximum likelihood method. Figure 1 shows the temporal distribution of aftershocks since occurrence of 2001 Bhuj earthquake mainshock i.e. from January 26, 2001 to December 31, 2014.
3. Results and Discussion
As discussed earlier, the entire aftershock sequence is divided in three series; series 1 for first 365-days, includes aftershocks from the next hour of the occurrence of the mainshock, i.e. January 26, 2001 to January 25, 2002;
Figure 1. Temporal magnitude distribution for the aftershock sequence of 2001 Bhuj earthquake.
series 2 includes aftershocks from January 26, 2001 to the occurrence of maximum magnitude aftershock of the entire sequence M ~ 5.7 on March 7, 2006 and series 3 includes the aftershocks for the entire aftershock sequence i.e. from January 26, 2001 to December 31, 2014. The decay of aftershocks with Omori law is studied for all these three series and displayed in Figures 2-4 along with values of three parameters p, c and K.
It can be observed that Figure 1 represents aftershocks immediate after the mainshock to the year ending of 2014. From the Figures 2-4, we can observe the decay curves the results of the studies that three series having the aftershock productivity in terms of the number of aftershocks as well as the Omori law decay parameter p that varies significantly from series 1 to series 3. It can be seen from Figure 4, i.e., decay curve for the entire aftershock sequence that initial decay rate of aftershocks is very fast and after approximate 120 days of the main shock, it has become slow; roughly after 400 days it has become almost constant up to approximate 1850 days and then again there is visible decay in the rate, another steadiness is observed at approximate after 4100 days. We now discuss Omori law parameters of p, c and K. Of these three parameters, p is the most important. The Omori law decay parameter p having the value of 1.06, 0.74 and 0.35 for the series 1, series 2 and series 3 respectively. It is assumed that the exponent p is 1.0, its typical value in empirical studies according to Utsu et al. (1995), Kagan (2004) and Gerstenberger et al. (2005) [10] [13] [14] . Previously, Mandal et al. (2007) found the p-value 0.99 for Bhuj aftershock sequence for the period from 2001 to 2005 [15] . A high p-value means that the rate of aftershocks decays faster with time than for a lower value of p. In view of its importance, the Omori law decay parameter p has received most attention in studies of aftershock sequences since the formulation of Omori’s law in 1894; aftershock sequences for both shallow and deep mainshocks have been studied in different tectonic environments such as oceanic spreading centers and transform faults, continental transform fault zones, continental collision zones and subduction zone environments. According to Utsu et al. (1995) the published values of p varies between 0.6 and 2.5 with a median of 1.1 whereas Kisslinger and Jones (1991) reported the p-values to be in the range 0.7 to 1.8 with a mean of 1.1 for shallow aftershock sequences in California. For the oceanic earthquakes, Bohnenstiehl et al. (2002) found p-values of 1.74 and 2.37 for two aftershock sequences associated with the spreading of the mid-Atlantic ridge and p-values in the range of 0.94 to 1.29 for three aftershock sequences associated with transform faults offsetting the ridge. Many researchers have studied the depth dependency of aftershock activity. Some of interesting results are discussed here briefly. Davis and Frohlich (1987) studied shallow and intermediate depth earthquakes and found that earthquakes occurring at depths greater than 70 km have the fewest and the smallest aftershock sequences [16] . He concluded that shallow subduction zone earthquakes produce more aftershocks than shallow ridge-transform zone earthquakes. Whereas Pavlis and Hamburger (1991) studied earthquakes in Pamir-Hindu Kush region and found that intermediate depth earthquakes in a collision plate boundary setting are capable of producing aftershock sequences. Results on studies of aftershock sequences in subduction zones are again very interesting. Wiens and Gilbert (1996) found that earthquakes as deep as ~650 km may be very productive in terms of the number of aftershocks; the 564 km deep Mw 7.6 Tonga earthquake and the 631 km deep Mw 8.3 Bolivia earthquake occurred in 1994, are earthquakes those produced aftershocks [17] - [19] . On the contrary, deep earthquakes in Japan and Indonesia
Figure 2. Omori law decay curve for first 365 days from the occurrence of 2001 Bhuj mainshock.
Figure 3. Omori law decay curve for the series of occurrence of 2001 Bhuj mainshock to occurrence of March 2006 moderate earthquake of M 5.7.
Figure 4. Omori law decay curve for the entire aftershock sequence from the occurrence of 2001 Bhuj mainshock to December 31, 2014.
have shown very low or no aftershock productivity [18] . The p-value is 1.19 and 1.006 for the deep 1994 Tonga and Bolivia earthquakes respectively. 2001 Bhuj earthquake of Mw 7.7 is the example of large SCR earthquake and it is of shallow focused and the aftershock activity is still ongoing over the Kachchh region. A general observation regarding the value of p is that it shows no correlation with either the magnitude of the mainshock or the cutoff magnitude Mc [7] [10] . The parameter p may therefore be interpreted to reflect properties of the fault system and the surrounding rock material [20] -[22] . On the otherhand, a correlation between high p-values and high surface heat flow has been observed and discussed by several authors [7] [20] [23] . Bohnenstiehl et al. (2002) concluded that higher p-values in ridge settings may be consistent with the higher temperature associated with spreading centers and continuous study is required to determine whether high p-values are the characteristic of spreading environments [9] . A connection between Omori decay law aftershock rate and stress fluctuation of a random Brownian motion type was proposed by Kagan and Knopoff (1987) [24] . Mogi (1962), Kisslinger and Jones (1991) and Utsu et al. (1995) tried to relate factors such as structural heterogeneity, stress and temperature in crust with the variability in p-value and concluded that which of these factors is most significant in controlling the value of p is not clear. Thus the number of aftershocks and decay parameter p, both varies significantly for different tectonic regimes [7] [10] [25] .
Another two components of Omori law K and c provide important insight into aftershocks behavior. The K-value depends on the total number of events in the sequence and reflects the earliest part of the sequence and accounts for the observed fact that the earliest aftershocks do not follow a steady decay rate rather their rate increases in the first minutes to hours, then begins to decrease [21] . It is found value of K for the present work 638.5, 179.9 and 29 for series 1, series 2 and series 3 respectively. Due to the intense aftershock activity at short times after the mainshock, the parameter c in Omori’s law is commonly considered as a time offset accounting for incomplete detection of aftershocks (e.g. Utsu et al., 1995; Kisslinger, 1996; Woessner et al., 2004) [10] [21] [26] . The parameter c in equation 2 is almost always found to be positive and typically ranges from 0.5 to 20 hour in empirical studies [10] [27] [28] . The positive value of c describes a saturation of aftershock rate close to the earthquake origin time. Such a saturation in aftershock rate has been observed in many aftershock sequences by Reasenberg & Jones (1989, 1994) and Utsu et al. (1995). The saturation is usually interpreted as a delay between mainshock rupture end and the start of aftershock activity [29] [30] . Accordingly, positive c from equation 2 means the singularity in equation 2 occurs before the mainshock and negative c means the singularity occurs after the mainshock. In the present study, for Bhuj aftershock sequence, positive value of c is found for all three series. For series 1 it is 5, for series 2 it is 2.325 and for series 3 it is 0.01. Shcherbakov et al. (2004) found that the parameter c in Omori’s law decreases as the magnitude of earthquakes considered increases. The physical models of aftershock behaviour can provide explanations for Omori’s law including a non-zero value of c. However, how to interpret c is always remain a controversial topic amongst seismologists. On the other hand, though the behavior of the decay parameter p is independent of cutoff magnitude; another two Omori law parameters K and c exhibit significant variation with the cutoff magnitude used. Using data from the 1993 Hokkaido-Nansei-Oki aftershock sequence, Utsu et al. (1995) showed that increasing the cutoff magnitude results in lowering the values of both K and c. An implication of this is that there is a possibility that K and c are not independent to each other and they in some way reflect the physical processes. However, Utsu et al. (1995) pointed out that positive values of c have been observed for adequately recorded aftershock sequences. The implication of positive c in all three series of Bhuj aftershock sequence in the present work is adequate records of aftershock sequence.
4. Conclusion
The analysis of aftershock sequence of the 2001 Bhuj earthquake (Mw 7.7) suggests that the seismic activity associated with some moderate events in 2006 had an influence on the future seismicity in the area, in particular on the temporal distribution of p-values observed for the aftershocks of 2001 Bhuj earthquake. The initial decay rate after the 2001 Bhuj mainshock was higher and later the decay rate is decreased significantly. Even though till the date the decay curve for 2001 Bhuj aftershock sequence is not found parallel to the time axis which suggests that more aftershocks are expected over the region and it may continue for a long. Using the temporal distribution of the aftershock sequence and the modified Omori’s law, the rate of aftershock occurrence can be forecasted and we can forecast the aftershock activity in the next 100 days, 365 days, 730 days and so on and compare it to the actually observed rates. The 2001 Bhuj aftershock sequence is well modeled by the modified Omori law and the p-value is found to be decreased from the initial to the later time of the sequence. The modified Omori’s law is the best option to describe aftershock activity and decay rates amongst exponential and other functions. The close examination of the decay curves presented in this study indicates that though the general decay trend is exponential, the plot of actual aftershocks occurring after 2001 Bhuj mainshock is distributed in a sinusoidal pattern which suggests the stress release mechanism of tectonics may be in a cyclical route. The results presented in this study are consistent with the existing knowledge about decay properties of aftershocks for different earthquakes recorded in different regions of the world.
Acknowledgements
The author is grateful to India Meteorological Department for providing valuable data and permission to publish the work and to Institute of Seismological Research for catalogue data. I am thankful to Dr. Jayanta Sarkar, Director, IMD, Ahmedabad for his kind co-operation.
Cite this paper
Parul C.Trivedi, (2015) Application of Omori’s Decay Law to the 2001 Bhuj Aftershock Sequence for Kachchh Region of Western India. Open Journal of Earthquake Research,04,94-101. doi: 10.4236/ojer.2015.43009
References
- 1. Negishi, H., Mori, J., Sato, T., Singh, R., Kumar, S. and Hirata, N. (2002) Size and Orientation of the Fault Plane for the 2001 Gujarat, India Earthquake (Mw 7.7) from Aftershock Observations: A High Stress Drop Event. Geophysical Research Letters, 29, 1989. http://dx.doi.org/10.1029/2002GL015280
- 2. Biswas, S.K. (2005) A Review of Structure and Tectonics of Kachchh Basin, Western India, with Special Reference to Earthquake. Current Science, 88, 1592-1600.
- 3. Mukhopadhyay, S. and Kayal, J.R. (2008) The 2001 Bhuj Earthquake (Mw 7.7) in Western India: 3D Velocity Structure and Seismotectonics Processes. Acta Geodaetica et Geophysica Hungarica, 43, 75-92. http://dx.doi.org/10.1556/AGeod.43.2008.1.6
- 4. Singh, A.P., Mishra, O.P., Rastogi, B.K. and Kumar, D. (2011) 3-D Seismic Structure of the Kachchh, Gujarat and Its Implications for the Earthquake Hazard Mitigation. Natural Hazards, 57, 83-105. http://dx.doi.org/10.1007/s11069-010-9707-2
- 5. Trivedi, P.C., Joshi, H.P. and Parvez, I.A. (2014) A Preliminary Study on Rainfall Pattern before and after the January 26, 2001 Bhuj Earthquake (Mw 7.7) over Kachchh Region of Western Peninsular India. International Journal of Geosciences, 5, 1080-1087. http://dx.doi.org/10.4236/ijg.2014.510092
- 6. Omori, F. (1894) On the Aftershocks of Earthquakes. Journal of the College of Science, Imperial University of Tokyo, 7, 111-120.
- 7. Kisslinger, C. and Jones, L.M. (1991) Properties of Aftershock Sequences in Southern California. Journal of Geophysical Research, 96, 947-958. http://dx.doi.org/10.1029/91jb01200
- 8. Pavlis, G.L. and Hamburger, M.W. (1991) Aftershock Sequences of Intermediate-Depth Earthquakes in the Pamir-Hindu Kush Seismic Zone. Journal of Geophysical Research, 96, 18107-18117. http://dx.doi.org/10.1029/91JB01510
- 9. Bohnenstiehl, D.R., Tolstoy, M., Dziak, R.P., Fox, C.G. and Smith, D.K. (2002) Aftershocks in the Mid-Ocean Ridge Environment: An Analysis Using Hydroacoustic Data. Tectonophysics, 354, 49-70. http://dx.doi.org/10.1029/91JB01510
- 10. Utsu, T., Ogata, Y. and Matsu’ura, R.S. (1995) The Centenary of the Omori Formula for a Decay Law of Aftershock Activity. Journal of Physics of the Earth, 43, 1-33. http://dx.doi.org/10.4294/jpe1952.43.1
- 11. Utsu, T. (1957) Magnitudes of Earthquakes and Occurrence of Their Aftershocks. Zisin, Ser. 2, 10, 35-45. (In Japanese)
- 12. Shcherbakov, R., Turcotte, D.L. and Rundle, J.B. (2004) A Generalized Omori’s Law for Earthquake Aftershock Decay. Geophysical Research Letters, 31, Article ID: L11613. http://dx.doi.org/10.1029/2004gl019808
- 13. Kagan, Y.Y. (2004) Short-Term Properties of Earthquake Catalogs and Models of Earthquake Source. Bulletin of the Seismological Society of America, 94, 1207-1228. http://dx.doi.org/10.1785/012003098
- 14. Gerstenberger, M.C., Wiemer, S., Jones, L.M. and Reasenberg, P.A. (2005) Real-Time Forecasts of Tomorrow’s Earthquakes in California. Nature, 435, 328-331. http://dx.doi.org/10.1038/nature03622
- 15. Mandal, P., Chadha, R.K., Raju, I.P., Kumar, N., Satyamurty, C. and Narsaiah, R. (2007) Are the 7 March 2006 Mw 5.6 Event and the 3 February 2006 Mw 4.58 Event Triggered by the Five Years Continued Occurrence of Aftershocks of the 2001 Mw 7.7 Bhuj Event? Current Science, 92, 1114-1124.
- 16. Frohlich, C. (1987) Aftershocks and Temporal Clustering of Deep Earthquakes. Journal of Geophysical Research, 92, 13944-13956. http://dx.doi.org/10.1029/JB092iB13p13944
- 17. Wiens, D.A., McGuire, J.J., Shore, P.J., Bevis, M.G., Draunidalo, K., Prasad, G. and Helu, S.P. (1994) A Deep Earthquake Aftershock Sequence and Implications for the Rupture Mechanism of Deep Earthquakes. Nature, 372, 540-543. http://dx.doi.org/10.1038/372540a0
- 18. Wiens, D.A. and Gilbert, H.J. (1996) Effect of Slab Temperature on Deep-Earthquake Aftershock Productivity and Magnitude-Frequency Relations. Nature, 384, 153-156. http://dx.doi.org/10.1038/384153a0
- 19. Nyffenegger, P. and Frohlich, C. (2000) Aftershock Occurrence Rate Decay Properties for Intermediate and Deep Earthquake Sequences. Geophysical Research Letters, 27, 1215-1218. http://dx.doi.org/10.1029/1999gl010371
- 20. Mogi, K. (1967) Earthquake and Fractures. Tectonophysics, 5, 35-55. http://dx.doi.org/10.1016/0040-1951(67)90043-1
- 21. Kisslinger, C. (1996) Aftershock and Fault Zone Properties. Advances in Geophysics, 38, 1-36. http://dx.doi.org/10.1016/S0065-2687(08)60019-9
- 22. Nanjo, K.Z., Enescu, B., Shcherbakov, R., Turcotte, D.L., Iwata, T. and Ogata, Y. (2007) Decay of Aftershock Activity for Japanese Earthquakes. Journal of Geophysical Research, 112, Article ID: B08309. http://dx.doi.org/10.1029/2006jb004754
- 23. Rabinowitz, N. and Steinberg, D.M. (1998) Aftershock Decay of Three Recent Strong Earthquakes in the Levant. Bulletin of the Seismological Society of America, 88, 1580-1587.
- 24. Kagan, Y.Y. and Knopoff, L. (1987) Random Stress and Earthquake Statistics: Time Dependence. Geophysical Journal International, 88, 723-731. http://dx.doi.org/10.1111/j.1365-246X.1987.tb01653.x
- 25. Mogi, K. (1962) Magnitude-Frequency Relationship for Elastic Shocks Accompanying Fractures of Various Materials and Some Related Problems in Earthquakes. Bulletin of the Earthquake Research Institute, University of Tokyo, 40, 831-853.
- 26. Woessner, J., Hauksson, E., Wiemer, S. and Neukomm, S. (2004) The 1997 Kagoshima (Japan) Earthquake Doublet: A Quantitative Analysis of Aftershock Rate Changes. Geophysical Research Letters, 31, Article ID: L03605. http://dx.doi.org/10.1029/2003gl018858
- 27. Reasenberg, P.A. and Jones, L.M. (1994) Earthquake Aftershocks: Update. Science, 265, 1251-1252. http://dx.doi.org/10.1126/science.265.5176.1251
- 28. Reasenberg, P.A. and Jones, L.M. (1989) Earthquake Hazard after a Mainshock in California. Science, 243, 1173-1176. http://dx.doi.org/10.1126/science.243.4895.1173
- 29. Rundle, J.B., Turcotte, D.L., Shcherbakov, R., Klien, W. and Sammis, C. (2003) Statistical Physics Approach to Understanding the Multiscale Dynamics of Earthquake Fault Systems. Reviews of Geophysics, 41, 1019. http://dx.doi.org/10.1029/2003RG000135
- 30. Kanamori, H. and Brodsky, E.E. (2004) The Physics of Earthquakes. Reports on Progress in Physics, 67, 1429-1496. http://dx.doi.org/10.1088/0034-4885/67/8/R03





