Open Journal of Optimization
Vol.05 No.04(2016), Article ID:73234,20 pages
10.4236/ojop.2016.54013
Intermodal Freight Network Design for Transport of Perishable Products
Maxim A. Dulebenets*, Eren E. Ozguven, Ren Moses, Mehmet B. Ulak
Department of Civil & Environmental Engineering, Florida A&M University-Florida State University, Tallahassee, FL, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 2, 2016; Accepted: December 27, 2016; Published: December 30, 2016
ABSTRACT
The amount of perishable products transported via the existing intermodal freight networks has significantly increased over the last years. Perishable products tend to decay due to a wide range of external factors. Supply chain operations mismanagement causes waste of substantial volumes of perishable products every year. The heretofore proposed mathematical models optimize certain supply chain processes and reduce decay of perishable products, but primarily deal with local production, inventory, distribution, and retailing of perishable products. However, significant quantities of perishable products are delivered from different continents, which shall increase the total transportation time and decay potential of perishable products as compared to local deliveries. This paper proposes a novel optimization model to design the intermodal freight network for both local and long-haul deliveries of perishable products. The objective of the model aims to minimize the total cost associated with transportation and decay of perishable products. A set of piecewise approximations are applied to linearize the non-linear decay function for each perishable product type. CPLEX is used to solve the problem. Comprehensive numerical experiments are conducted using the intermodal freight network for import of the seafood perishable products to the United States to draw important managerial insights. Results demonstrate that increasing product decay cost may significantly change the design of intermodal freight network for transport of perishable products, cause modal shifts and affect the total transportation time and associated costs.
Keywords:
Freight Transportation, Network Design, Perishable Products, Shelf Life, Optimization

1. Introduction
Many of products transported via intermodal freight networks are perishable in their nature. Perishable products (such as agricultural products, meat, fish, shellfish, pharmaceutical products, etc.) are sensitive to a wide range of different factors, which include but are not limited to temperature, barometric pressure, humidity, air composition and transportation time [1] [2] [3] . The demand for perishable products has been continuously growing. According to National Oceanic and Atmospheric Administration (NOAA), the total volume of seafood perishable products, which have been imported to the United States (US), increased by 7.6% over the last five years and reached 2.7 million tons in 2015 [4] . Furthermore, the value of seafood perishable products, which have been delivered to the US, increased by 13.2% over the last five years and reached $19.2 billion in 2015 [4] . Peeled frozen shrimp, frozen tilapia fillet, and fresh Atlantic farm raised salmon are the top three seafood perishable products, which are imported to the US mainly from India, China, and Chile respectively [4] .
Refrigerated containers (a.k.a., “reefers”) are generally used for transport of perishable food products. Reefers are able to maintain a certain temperature and decrease physiological, microbiological, and physical changes in the perishable product [5] . Reefers allow slowing down decay of perishable products, but do not completely eliminate it. Due to temperature deviations within the containers perishable products may continue ripening. For example, the daily ripening rate of bananas may increase up to ~75% from increasing the temperature inside a given container from 15˚C to 20˚C [5] . Each perishable product must be delivered via the freight transportation network to the customer before the end of its “shelf life”, which represents the number of remaining days for a given perishable product to be of an acceptable quality for consumption. To obtain the information regarding the perishable product quality throughout the transportation process, many freight carries rely on the advanced information technologies. Radio-Frequency Identification (RFID) is one of the most frequently used technologies for traceability of perishable products within containers [3] [5] [6] .
Implementation of refrigerated containers and RFID technology for transporting perishable products and tracking their quality allows decreasing waste of perishable products, but does not completely eliminate it. Mismanagement of operations within supply chains may cause from 20% to 60% of wasted agricultural products in a given country [7] . Furthermore, Rodrigue [8] reports that approximately 25% of perishable products are spoilt during their transportation process every year due to variations in temperature and other factors, which can further speed up the product deterioration. According to the World Trade Organization (WTO), the total value of food exports reached $1486 billion in 2014 [9] . Hence, the cost associated with decay of perishable products is extremely high. A large number of studies have been conducted in the past aiming to optimize certain supply chain processes and reduce decay of perishable products. However, those studies mostly focused on local production, inventory, distribution (by one transportation mode-trucks), and retailing of perishable products [1] [2] [3] [10] - [18] . Nevertheless, substantial quantities of perishable products are delivered from different continents, which shall increase the total transportation time as compared to local deliveries. Furthermore, the decay potential of perishable products in case of operations mismanagement is significantly higher for long-haul deliveries and compared to local deliveries.
Therefore, there is a need for more comprehensive models to design the intermodal freight network that would allow selection of the appropriate transportation routes and transportation modes for shipments with perishable products. This paper aims to fill the existing gap in the state-of-the-art and proposes a novel optimization model for efficient management of supply chains with perishable products that can be used for both local and long-haul deliveries. The objective of the model aims to minimize the total cost associated with transportation and decay of perishable products. A set of piecewise approximations are applied to linearize the non-linear decay function for each perishable product type, and the resulting mixed integer linear problem is solved using CPLEX. Numerical experiments are performed using the intermodal freight network for import of the seafood perishable products to the US. The rest of the manuscript is organized as follows. The next section provides a detailed problem description, while the third section presents the mathematical model and the solution methodology. The fourth section describes a set of numerical experiments conducted to evaluate performance of the adopted solution methodology and reveal important managerial insights using the developed mathematical model. The last section summarizes the study findings and proposes directions for the future research.
2. Problem Description
This section of the paper focuses on description of the main problem features, including the following: 1) network elements; 2) cargo transfer within intermodal terminals; 3) perishability modeling; 4) shelf life of perishable shipments; and 5) decisions.
2.1. Network Elements
An example of the intermodal freight network is presented in Figure 1. Let 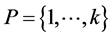 be a set of perishable shipments. Each perishable shipment is assumed to have an origin terminal and a destination terminal (see Figure 1). The origin and destination terminals of the perishable shipments are connected with a set of transportation routes
be a set of perishable shipments. Each perishable shipment is assumed to have an origin terminal and a destination terminal (see Figure 1). The origin and destination terminals of the perishable shipments are connected with a set of transportation routes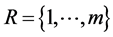 . Each route is divided in a set of route segments
. Each route is divided in a set of route segments . At each segment the shipping company is able to select a transportation mode (i.e., sea, air, rail, truck, etc.) out of the set of modes
. At each segment the shipping company is able to select a transportation mode (i.e., sea, air, rail, truck, etc.) out of the set of modes . It is assumed that availability of modes varies from one route segment to another (e.g., at route segments passing through sea the shipping company can transport the perishable shipment either by sea or air, while at land route segments the shipping company can transport the perishable shipment either by air or rail or truck). The transportation time
. It is assumed that availability of modes varies from one route segment to another (e.g., at route segments passing through sea the shipping company can transport the perishable shipment either by sea or air, while at land route segments the shipping company can transport the perishable shipment either by air or rail or truck). The transportation time 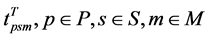 (measured in hours) and associated cost
(measured in hours) and associated cost 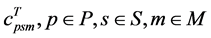 (measured in USD) of a given perishable shipment at each route segment are assumed to vary depending on the transportation mode selected. For example, the transportation time of a given perishable shipment by air will be shorter as compared to truck, but it will incur a higher cost for the shipping company.
(measured in USD) of a given perishable shipment at each route segment are assumed to vary depending on the transportation mode selected. For example, the transportation time of a given perishable shipment by air will be shorter as compared to truck, but it will incur a higher cost for the shipping company.
Figure 1. Intermodal freight network example.
2.2. Cargo Transfer within Intermodal Terminals
A transfer of perishable shipments from one mode to another occurs within the intermodal terminals (see Figure 1). The handling time at the intermodal terminal 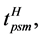
 (measured in hours) and associated cost
(measured in hours) and associated cost  (measured in USD) are assumed to vary depending on the type of a perishable shipment (captured by index
(measured in USD) are assumed to vary depending on the type of a perishable shipment (captured by index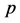 ), route segment (captured by index
), route segment (captured by index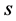 ), and mode selected for transport at a given route segment (captured by index
), and mode selected for transport at a given route segment (captured by index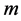 ). The latter allows tackling the change in handling time and cost of a given perishable shipment due to its size (e.g., increasing size of shipments will increase the handing time), mode availability depending on the route segment selected, and required resources for transfer of a cargo from one mode to the other.
). The latter allows tackling the change in handling time and cost of a given perishable shipment due to its size (e.g., increasing size of shipments will increase the handing time), mode availability depending on the route segment selected, and required resources for transfer of a cargo from one mode to the other.
2.3. Perishability Modeling
The quality of perishable products within each shipment is assumed to deteriorate over time. Increase in the total transportation time (which includes the total transportation time along the route segments of the selected route and the total handling time at the intermodal terminals) negatively affects freshness of products in each shipment. Each perishable shipment is assumed to be homogenous (i.e., each shipment is composed of perishable products of the same nature, which deteriorate at the same rate over time). Based on the available literature, the quality of a perishable product in shipment 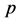 at a given time
at a given time  can be estimated based on the following equation [2] , [3] , [16] , [17] :
can be estimated based on the following equation [2] , [3] , [16] , [17] :
 (1)
(1)
where:
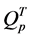 ―is the quality of a perishable product in shipment
―is the quality of a perishable product in shipment  at time
at time 






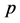
The decay rate 
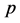
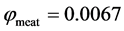


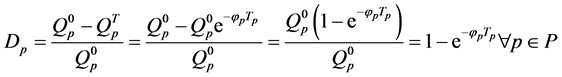
Note that decay function 





Let 








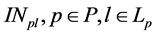




Figure 2. Piecewise linear approximations for the product decay function.



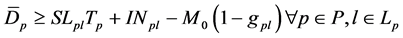
Constraints set (3) indicates that only one segment of the piecewise function should be selected for approximation of the decay function for a perishable product in a given shipment. Constraints sets (4) and (5) define the range of the total transportation time values, when a given linear segment should be used to approximate the decay function for a perishable product in a given shipment. Constraints set (6) computes the approximated decay of a perishable product in a given shipment at the destination terminal.
2.4. Shelf Life of Perishable Shipments
As discussed in the introduction section of the paper, perishable products should be delivered to their destinations before the end of their shelf lives in order to be of an acceptable quality for the consumers. This study captures the latter operational aspect by imposing the following constraints set for each perishable shipment

where:

Constraints set (7) ensures that each perishable shipment will be delivered to its destination before the end of its shelf life.
2.5. Decisions
In this problem, the shipping company needs to make the following two major decisions: a) select a route for transportation of each perishable shipment; and b) choose a transportation mode at each segment of the selected route for each perishable shipment. Both decisions should account for a number of factors such as: 1) transportation mode availability at a given route segment; 2) increasing transportation cost for selection of faster transportation mode (e.g., transportation time by air will be smaller than by sea, but will incur higher transportation costs); 3) handling time at the intermodal terminals depending on selected mode (e.g., loading containers on a vessel may take longer as compared to loading containers on a train); 4) increasing product decay costs due to increasing total transportation time; 5) decay rate of a perishable product in a given shipment (e.g., higher decay rate will require the shipping company to select faster transportation modes at route segments to ensure that the products will be delivered to their destination terminal before the end of their shelf life).
3. Mathematical Model
This section presents notations that will be further used throughout the paper and a mixed integer mathematical model for the intermodal freight network design problem with perishable products.
3.1. Notations
Sets
Decision variables
Auxiliary variables
Parameters
3.2. Model Formulation
The mixed integer mathematical model for the intermodal freight network design problem with perishable products (IFNDP) can be formulated as follows:
IFNDP:
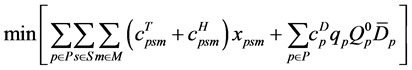
Subject to:
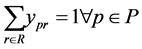




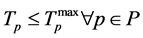







In IFNDP, the objective function (8) aims to minimize the total cost associated with transportation of perishable shipments, handling of perishable shipments at the intermodal terminals, and decay of perishable shipments throughout the transportation process. Constraints set (9) ensures that only one route should be selected for transport of a given perishable shipment. Constraints set (10) indicates that the route for transport of a given perishable shipment should be selected only from the routes available for transport of that particular shipment. Constraints set (11) ensures that a given perishable shipment should be transported along all the segments of the selected route. Constraints set (12) ensures that the mode for transport of a given perishable shipment should be selected only from the modes available for transport of that particular shipment at a given route segment. Constraints set (13) estimates the total transportation time of a given perishable shipment. Constraints set (14) ensures that each perishable shipment will be delivered to its destination before the end of its shelf life. Constraints set (15) indicates that only one segment of the piecewise function should be selected for approximation of the decay function for a perishable product in a given shipment. Constraints sets (16) and (17) define the range of the total transportation time values, when a given linear segment should be used to approximate the decay function for a perishable product in a given shipment. Constraints set (18) computes the approximated decay of a perishable product in a given shipment at the destination terminal. Constraints sets (19)-(21) define the nature of IFNDP variables and parameters.
3.3. Solution Methodology
Application of the piecewise linear approximations for the product decay functions allows formulating IFNDP as a mixed integer linear mathematical model, which can be solved using commercial optimization solvers (e.g., CPLEX) within an acceptable computational time even for large size problem instances (as will be discussed in the numerical experiments section).
4. Numerical Experiments
This section of the paper describes a set of numerical experiments that were performed to assess efficiency of the proposed solution methodology and reveal important managerial insights using the developed mathematical model.
4.1. Input Data Generation
The numerical data for computational experiments were generated based on the academic literature and publicly available resources [19] - [30] . A total of top ten seafood perishable product types, based on the overall volumes imported to the US, were considered in this study. The top origin country and the top five US destinations (based on the overall volumes) for each perishable product type were retrieved using the data provided by NOAA [4] and are presented in Table 1.
The intermodal freight network for transport of perishable products (see Figure 3) included 5 marine terminals, 40 rail terminals, and 50 destination depots. Locations of the intermodal terminals were retrieved using the data provided by the Intermodal Association of North America [19] . Each shipment was assumed to originate at one of the marine terminals of the top exporting country. A total of 50 possible routes were considered for each origin-destination pair. The intermodal freight network was composed of 350 route segments. Since seafood perishable products are rarely transported
Figure 3. Intermodal freight network modeled.
Table 1. Origins and destinations by product type.
by air, a total of three transportation modes were considered: 1) road; 2) rail; and 3) sea (i.e., a set of modes is
The transportation cost of a perishable shipment was assigned based on the unit transportation cost by mode (

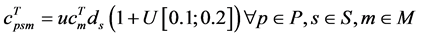




mph) as follows: 
time of a perishable shipment at the intermodal terminals was computed based on the average handling time by mode (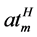
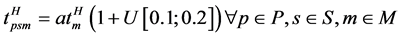

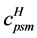





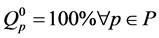

All numerical experiments were conducted on a Dell Intel(R) CoreTM i7 Processor with 32 GB of RAM. IFNDP mathematical model was coded in General Algebraic Modeling System (GAMS, [31] ) and solved using CPLEX. Piecewise linear approximations for product decay functions were developed using MATLAB 2016a [32] .
4.2. Solution Methodology Evaluation
As discussed in section 2.3 of the paper, increasing number of segments in the piecewise approximation increases accuracy of estimating the product decay values and the objective function itself, but may increase the computational time required to solve IFNDP mathematical model. A total of 25 problem instances were generated using the retrieved data, described in section 4.1, to analyze the latter tradeoff by changing the number of perishable shipments to be transported (from 2 to 10 shipments) and the number of linear segments in the piecewise approximation (from 10 to 100 segments). Detailed information regarding each shipment is provided in Table 3, including the following data: 1) shipment number; 2) perishable product type; 3) origin country; 4) US destination (randomly selected out of top five US destinations for a given product type); and 5) quantity of perishable products shipped. For example, the first shipment includes 1294 units/packages of shrimp warm-water peeled frozen and is imported from India to New York (NY).
IFNDP was solved for each one of the developed problem instances, and results are presented in Table 4, including the following information: 1) instance number; 2)
Table 2. Numerical data.
Table 3. Shipment characteristics.
Table 4. Solution methodology performance.
number of shipments; 3) number of linear segments in the piecewise approximations; 4) total number of variables in IFNDP mathematical model; 5) average over all shipments product decay estimated based on piecewise approximations―

average product decay gap―
based on piecewise approximations―


We observe that increasing the number of segments in the piecewise function from 10 to 100 segments on average reduces the product decay and objective function gaps by 98.46% and increases the computational time only by 17.24%. Furthermore, the computational time over all the generated problem instances did not exceed 0.49 sec. The latter results demonstrate efficiency of the proposed solution approach, considering the fact that relatively large size problem instances were analyzed with up to 12,024 variables. The computational time may increase for larger intermodal freight networks. Application of the developed mathematical model for larger intermodal freight networks can be one of the future research directions of this study. Piecewise approximations with 100 segments will be further adopted for analysis of the managerial insights.
4.3. Managerial Insights
This section of the paper demonstrates how the developed optimization model can be used to draw important managerial insights. A total of 10 scenarios were developed for the problem instance with 10 perishable shipments by increasing the product decay cost as follows: 

4.3.1. Total Miles Traveled by Mode
The total miles traveled (TMT) by each mode were calculated for each one of the considered product decay cost scenarios, and results are presented in Figure 4. It can be noticed that increasing product decay cost reduces the TMT by rail and increases the TMT by road. The latter finding can be explained by the fact that the shipping company was required to use trucks for inland transport rather than trains in cases with high product decay costs, as trucks provide faster delivery of perishable products to the destination terminals and decrease the total product decay. Furthermore, the numerical experiments demonstrate that the TMT by sea was reduced with increasing product decay cost, which can be justified by selection of shorter sea routes to decrease the transportation time in sea.
Figure 4. Total miles traveled by mode and scenario.
Table 5. Product decay cost by shipment and scenario (USD).
4.3.2. Total Transportation Time and Product Decay
Throughout the numerical experiments the average total transportation time 

4.3.3. Cost Analysis
The scope of numerical experiments also included a detailed analysis of IFNDP cost components. The objective function and its components were estimated using the proposed mathematical model for each one the generated product decay cost scenarios. Results are presented in Figure 6, including the following cost components: 1) the total cost (i.e., objective function value)―


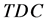
Furthermore, numerical experiments show that the total decay cost is still increasing from one scenario to the other despite decrease in the actual decay of perishable pro-
Figure 5. Average transportation time and product decay by scenario.
Figure 6. Objective function components by scenario.
ducts (see Section 4.3.2 for more details). The latter can be explained by marginal in- crease in the unit decay cost for each product (e.g., decrease of the product decay by 10% and increase of the unit product decay cost by 30% will still increase the total decay cost). It was found that the total cost associated with both transportation and decay of perishable products may be significantly affected with the product decay cost. Hence, decisions that have to be made by the shipping company will be substantially influenced depending on how the shipping company perceives the value of perishable products to be transported. In conclusion, the proposed mathematical model and solution methodology can serve as efficient practical tool in design of the intermodal freight network for both local and long-haul deliveries of perishable products and understanding of important tradeoffs.
5. Conclusions and Future Research
The amount of perishable products transported via the existing intermodal freight networks significantly increased over the last decade. Due to operations mismanagement within supply chains with perishable products drastic losses associated with the product decay have been reported. Moreover, published to date mathematical models primarily optimize supply chain processes that deal with local production, inventory, distribution, and retailing of perishable products. Nevertheless, many perishable product types are imported from different continents, which increases the total transportation time and decay potential as compared to local deliveries. Unlike previous models in the literature, this paper proposed a novel mathematical model to design the intermodal freight network for both local and long-haul deliveries of perishable products. The objective aimed to minimize the total cost associated with transport and decay of perishable products. A set of piecewise approximations were adopted to linearize the non-linear decay function for each perishable product type. CPLEX was used to solve the problem. Numerical experiments, conducted using the intermodal freight network for import of the seafood perishable products to the United States, demonstrated efficiency of the adopted solution methodology in terms of solution quality and computational time. Furthermore, it was found that decisions that have to be made by the shipping company in design of the intermodal freight network were significantly dependent on how the value of perishable products was perceived. The developed mathematical model can serve as an efficient practical tool to manage both local and long-haul deliveries of perishable products.
The scope of future research may include the following extensions: 1) apply the proposed mathematical model for larger intermodal freight networks; 2) consider different types of perishable products (e.g., agricultural products, meat, pharmaceutical products, human specimens, etc.); 3) model decay of perishable products due to other factors (e.g., temperature, humidity, barometric pressure, air composition); 4) deployment of alternative cost functions for inland transport of perishable products (e.g., which capture changes in the unit transportation cost for a given mode depending on the distance traveled and shipment weight); 5) account for uncertainty in product decay throughout the transportation process; 6) quantify reliability associated with transportation of perishable products by a given mode; 7) consider the effects of economies of scale; and 8) consider the effect of real-time delay and congestion.
Cite this paper
Dulebenets, M.A., Ozguven, E.E., Moses, R. and Ulak, M.B. (2016) Intermodal Freight Network Design for Transport of Perishable Products. Open Journal of Optimization, 5, 120-139. http://dx.doi.org/10.4236/ojop.2016.54013
References
- 1. Rong, A., Akkerman, R. and Grunow, M. (2011) An Optimization Approach for Managing Fresh Food Quality throughout the Supply Chain. International Journal of Production Economics, 131, 421-429.
https://doi.org/10.1016/j.ijpe.2009.11.026 - 2. Wang, X. and Li, D. (2012) A Dynamic Product Quality Evaluation Based Pricing Model for Perishable Food Supply Chains. Omega, 40, 906-917.
https://doi.org/10.1016/j.omega.2012.02.001 - 3. Grunow, M. and Piramuthu, S. (2013) RFID in Highly Perishable Food Supply Chains—Remaining Shelf Life to Supplant Expiry Date? International Journal of Production Economics, 146, 717-727.
https://doi.org/10.1016/j.ijpe.2013.08.028 - 4. NOAA (2016) Commercial Fisheries Statistics—US Foreign Trade Annual Data.
http://www.st.nmfs.noaa.gov/commercial-fisheries/foreign-trade/ - 5. Haass, R., Dittmer, P., Veigt, M. and Lutjen, M. (2015) Reducing Food Losses and Carbon Emission by Using Autonomous Control—A Simulation Study of the Intelligent Container. International Journal of Production Economics, 164, 400-408.
https://doi.org/10.1016/j.ijpe.2014.12.013 - 6. Aung, M. and Chang, Y. (2014) Temperature Management for the Quality Assurance of a Perishable Food Supply Chain. Food Control, 40, 198-207.
https://doi.org/10.1016/j.foodcont.2013.11.016 - 7. Widodo, K., Nagasawa, H., Morizawa, K. and Ota, M. (2006) A Periodical Flowering-Harvesting Model for Delivering Agricultural Fresh Products. European Journal of Operational Research, 170, 24-43.
https://doi.org/10.1016/j.ejor.2004.05.024 - 8. Rodrigue, J.-P., Comtois, C. and Slack, B. (2013) The Geography of Transport Systems. 3rd Edition, Routledge, New York.
- 9. WTO (2015) International Trade Statistics 2015. A Comprehensive Overview of World Trade.
https://www.wto.org/english/res_e/statis_e/its2015_e/its2015_e.pdf - 10. Ahumada, O. and Villalobos, J. (2011) A Tactical Model for Planning the Production and Distribution of Fresh Produce. Annals of Operations Research, 190, 339-358.
https://doi.org/10.1007/s10479-009-0614-4 - 11. Kopanos, G., Puigjaner, L. and Georgiadis, M. (2012) Simultaneous Production and Logistics Operations Planning in Semicontinuous Food Industries. Omega, 40, 634-650.
https://doi.org/10.1016/j.omega.2011.12.002 - 12. Li, Y., Cheang, B. and Lim, A. (2012) Grocery Perishables Management. Production and Operations Management, 21, 504-517.
https://doi.org/10.1111/j.1937-5956.2011.01288.x - 13. Amorim, P., Belo-Filho, M., Toledo, F., Almeder, C. and Almada-Lobo, B. (2013) Lot Sizing versus Batching in the Production and Distribution Planning of Perishable Goods. International Journal of Production Economics, 146, 208-218.
https://doi.org/10.1016/j.ijpe.2013.07.001 - 14. Bilgen, B. and Celebi, Y. (2013) Integrated Production Scheduling and Distribution Planning in Dairy Supply Chain by Hybrid Modelling. Annals of Operational Research, 211, 55-82. https://doi.org/10.1007/s10479-013-1415-3
- 15. Farahani, P. Grunow, M. and Akkerman, R. (2013) Design and Operations Planning of Municipal Food Service Systems. International Journal of Production Economics, 144, 383-396.
https://doi.org/10.1016/j.ijpe.2013.03.004 - 16. Piramuthu, S. and Zhou, W. (2013) RFID and Perishable Inventory Management with Shelf-Space and Freshness Dependent Demand. International Journal of Production Economics, 144, 635-640.
https://doi.org/10.1016/j.ijpe.2013.04.035 - 17. Yu, W. and Nagurney, A. (2013) Competitive Food Supply Chain Networks with Application to Fresh Produce. European Journal of Operational Research, 224, 273-282.
https://doi.org/10.1016/j.ejor.2012.07.033 - 18. Govindan, K., Jafarian, A., Khodaverdi, R. and Devika, K. (2014) Two-Echelon Multiple-Vehicle Location-Routing Problem with Time Windows for Optimization of Sustainable Supply Chain Network of Perishable Food. International Journal of Production Economics, 152, 9-28.
https://doi.org/10.1016/j.ijpe.2013.12.028 - 19. Intermodal Association of North America (2016) North American Intermodal Facilities Directory.
http://www.intermodal.org/information/directories/naifd.php - 20. Gonzales, D., Searcy, E. and Eksioglu, S. (2013) Cost Analysis for High-Volume and Long-Haul Transportation of Densified Biomass Feedstock. Transportation Research Part A, 49, 48-61.
https://doi.org/10.1016/j.tra.2013.01.005 - 21. The World Bank (2016) Cost to Import (US$ per Container).
http://data.worldbank.org/indicator/IC.IMP.COST.CD - 22. Dulebenets, M.A., Golias, M., Mishra, S. and Heaslet, W. (2015) Evaluation of the Floaterm Concept at Marine Container Terminals via Simulation. Simulation Modelling Practice and Theory, 54, 19-35.
https://doi.org/10.1016/j.simpat.2015.02.008 - 23. Dulebenets, M.A. (2015) Bunker Consumption Optimization in Liner Shipping: A Metaheuristic Approach. International Journal on Recent and Innovation Trends in Computing and Communication, 3, 3766-3776.
- 24. Dulebenets, M.A. (2015) Models and Solution Algorithms for Improving Operations in Marine Transportation. Dissertation, University of Memphis, Memphis.
- 25. The Port Authority of New York and New Jersey (2016) Marine Terminal Tariffs.
http://www.panynj.gov/port/tariffs.html - 26. US Department of Energy (2011) Fact #671: April 18, 2011 Average Truck Speeds.
http://energy.gov/eere/vehicles/fact-671-april-18-2011-average-truck-speeds - 27. Schoenbaum, M. (2013) CSX Explains Slower Train Speeds in Heat or Heavy Rain.
http://greatergreaterwashington.org/post/19569/csx-explains-slower-train-speeds-in-heat-or-heavy-rain/ - 28. Dulebenets, M.A. (2012) Highway-Rail Grade Crossing Identification and Prioritizing Model Development. MSc Thesis, University of Memphis, Memphis.
- 29. Dulebenets, M.A. (2016) A New Simulation Model for a Comprehensive Evaluation of Yard Truck Deployment Strategies at Marine Container Terminals. Open Science Journal, 1, 1-28.
- 30. Dulebenets, M.A. (2016) Vessel Scheduling Problem in a Liner Shipping Route with Heterogeneous Vessel Fleet. International Journal of Civil Engineering, 1-14.
https://doi.org/10.1007/s40999-016-0060-z - 31. GAMS (2016) GAMS Home Page.
https://www.gams.com/ - 32. MathWorks (2016) Release 2016a.
https://www.mathworks.com/








