Open Journal of Optimization
Vol.2 No.1(2013), Article ID:29434,7 pages DOI:10.4236/ojop.2013.21002
Solution of Matrix Game with Triangular Intuitionistic Fuzzy Pay-Off Using Score Function
1Bankura Christian College, Bankura, India
2Department of Applied Mathematics with Oceanology and Computer Programming, Vidyasagar University, Midnapore, India
Email: sibasisbanerjee@rediffmail.com, *nayak_ prasun@rediffmail.com, madhumangal@lycos.com
Received January 10, 2013; revised February 6, 2013; accepted March 4, 2013
Keywords: Triangular Intuitionistic Fuzzy Number; Matrix Game; Value Judgement Index; Score Function
ABSTRACT
Using score function in a matrix game is very rare. In the proposed paper we have considered a matrix game with pay-off as triangular intuitionistic fuzzy number and a new ranking order has been proposed using value judgement index, available definitions and operations. A new concept of score function has been developed to defuzzify the pay-off matrix and solution of the matrix game has been obtained. A numerical example has been given in support of the proposed method.
1. Introduction
Game theory is the way to handle the problems where two conflicting interests situation exist. But in modern society a lot of problems exist which cannot be explained in simple crisp sense e.g. there may be the situation where pay-offs are not known precisely. In such cases fuzzy mathematics is a tool to handle such situation. Fuzziness in matrix games can appear in many ways but two classes of fuzziness seem to be very natural. These two classes of fuzzy matrix games are referred to as matrix games with fuzzy goal [1] and matrix games with fuzzy pay off [2]. In recent times much attention has been drawn to interval valued game, Nayak and Pal [3-5], Narayanan [6], Nishizaki [1]. In practical situations the pay-offs are given with in certain ranges rather than as an exact number. These uncertain situations are overcome when we use interval numbers as pay-offs. An interval number is an extension of a real number and also a subset of a real line , Moore [7]. Zimmermann [8] shows that
, Moore [7]. Zimmermann [8] shows that  cut of a fuzzy number is an interval number. The method of solution of a matrix game using interval numbers was already established, Nayak and Pal [5]. In Narayanan [6], probability and possibility approaches have been used to solve a
cut of a fuzzy number is an interval number. The method of solution of a matrix game using interval numbers was already established, Nayak and Pal [5]. In Narayanan [6], probability and possibility approaches have been used to solve a 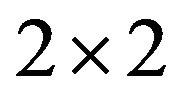 interval game but no certain distribution function has been used. Moreover, reduction of an
interval game but no certain distribution function has been used. Moreover, reduction of an  game to a
game to a 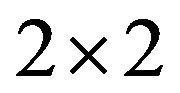 sub game is a basic problem in an interval game. In the dominance method [3], if the convex combination of any two rows(columns)of a pay-off matrix is dominated by the third row (column), it indicates that the third move of the row (column) of the player will be an optimal move but we are not certain as to which one of the first two moves will be an optimal one. This disadvantage is overcome through the graphical method [4]. But it may be the situation where the players can estimate the approximate pay-off values with some degree but there exist a hesitation. Such situations are handled by intuitionistic fuzzy (IF) numbers. Atanassov [9] first introduced the concept of IF-set where he explained an element of an IF-set in respect of degree of belongingness, degree of non-belongingness and degree of hesitancy. This degree of hesitancy is nothing but the uncertainty in taking a decision by a decision maker (DM). Atanassov [10] first described a game using the IF-set. Li and Nan [11] considered the matrix games with pay-offs as IF-sets. Seikh, Nayak and Pal [12] considered a bi-matrix game where they used IF-set. In this paper we have considered a matrix game where the pay-off elements are considered as triangular intuitionistic fuzzy number (TIFN). Nan, Li and Zhang [13] considered such TIFN as pay-off elements of the matrix and described the arithmetic operation and cut sets. In this paper, we have made a ranking order of the TIFN based on value judgement index and deviation indexe of membership and non-membership functions. A score function approach has been described to defuzzify the matrix. The numerical problem is a real life voting share problem and establishes the theory on strong ground.
sub game is a basic problem in an interval game. In the dominance method [3], if the convex combination of any two rows(columns)of a pay-off matrix is dominated by the third row (column), it indicates that the third move of the row (column) of the player will be an optimal move but we are not certain as to which one of the first two moves will be an optimal one. This disadvantage is overcome through the graphical method [4]. But it may be the situation where the players can estimate the approximate pay-off values with some degree but there exist a hesitation. Such situations are handled by intuitionistic fuzzy (IF) numbers. Atanassov [9] first introduced the concept of IF-set where he explained an element of an IF-set in respect of degree of belongingness, degree of non-belongingness and degree of hesitancy. This degree of hesitancy is nothing but the uncertainty in taking a decision by a decision maker (DM). Atanassov [10] first described a game using the IF-set. Li and Nan [11] considered the matrix games with pay-offs as IF-sets. Seikh, Nayak and Pal [12] considered a bi-matrix game where they used IF-set. In this paper we have considered a matrix game where the pay-off elements are considered as triangular intuitionistic fuzzy number (TIFN). Nan, Li and Zhang [13] considered such TIFN as pay-off elements of the matrix and described the arithmetic operation and cut sets. In this paper, we have made a ranking order of the TIFN based on value judgement index and deviation indexe of membership and non-membership functions. A score function approach has been described to defuzzify the matrix. The numerical problem is a real life voting share problem and establishes the theory on strong ground.
The paper is organized as follows: In Section 2, basic definitions of intuitionistic fuzzy set is given intuitionistic fuzzy number, TIFN and score function are defined and arithmetic operations are described. In Section 3, matrix game with TIFN pay-off, pure and mixed strategy have been described. In Section 4, numerical example is given. In Section 5 conclusion has been drawn.
2. Intuitionistic Fuzzy Sets
Here we are to introduce first some relevant basic preliminaries, notations and definitions of IFS, in particular the works of Atanassov [9,14].
Definition 1: Let 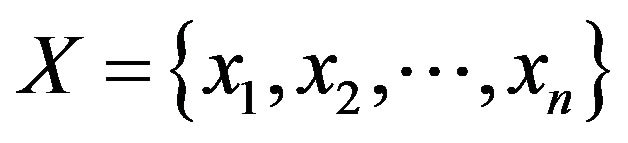 be a finite universal set. An Atanasson’s intuitionistic fuzzy set (IFS) in a given universal set
be a finite universal set. An Atanasson’s intuitionistic fuzzy set (IFS) in a given universal set  is an expression
is an expression  given by
given by
 (1)
(1)
where the functions
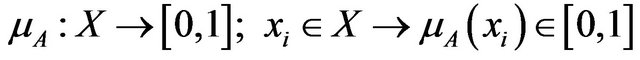
and 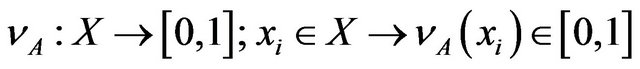 define the degree of membership and the degree of non-membership of an element
define the degree of membership and the degree of non-membership of an element  to the set
to the set , respectively, such that they satisfy the following condition: for every
, respectively, such that they satisfy the following condition: for every 
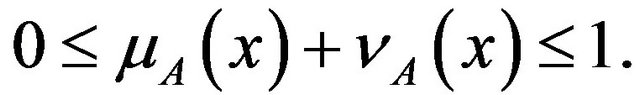
Let
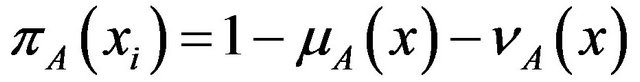
which is called the Atanassov’s [14] intuitionistic index of an element  in the set
in the set . It is the degree of indeterminacy membership of the element
. It is the degree of indeterminacy membership of the element  to the set
to the set
 . Obviously,
. Obviously,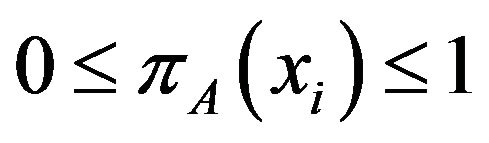 . If an Atanassov’s IFS
. If an Atanassov’s IFS  in
in 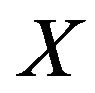 has only an element, then
has only an element, then 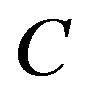 is written as follows
is written as follows
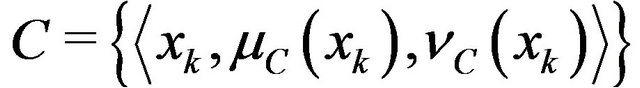
which is usually denoted by  for short.
for short.
Definition 2: Let  and
and 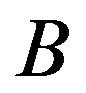 be two Atanassov’s IFSs in the set
be two Atanassov’s IFSs in the set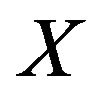 .
.  iff
iff
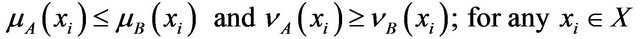 .
.
Definition 3: Let  and
and  be two Atanassov's IFSs in the set
be two Atanassov's IFSs in the set .
. 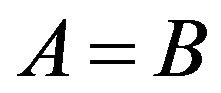 iff
iff
 Namely,
Namely, 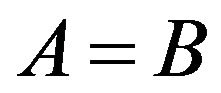 iff
iff  and
and .
.
Definition 4: Let  and
and  be two Atanassov’s IFSs in the set
be two Atanassov’s IFSs in the set . The intersection of
. The intersection of  and
and 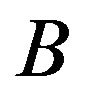 is defined as follows:
is defined as follows:

Definition 5: (Intuitionistic Fuzzy Number [15]): An intuitionistic fuzzy number (Figure 1)  is 1) an intuitionistic fuzzy subset of the real line;
is 1) an intuitionistic fuzzy subset of the real line;
2) normal, i.e. there exists 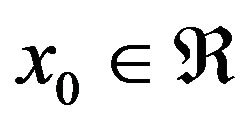 such that
such that 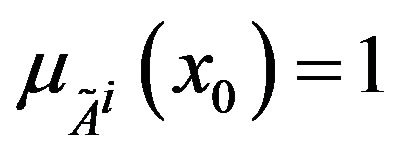 (so
(so );
);
3) convex for the membership function 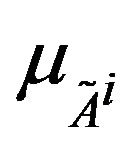 i.e.
i.e.
 ;
;
4) concave for the non-membership function 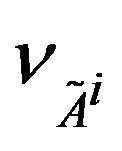 i.e.
i.e.

In our discussion we consider an intuitionistic fuzzy number 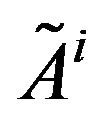 as
as 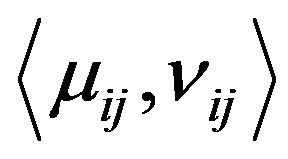 where
where 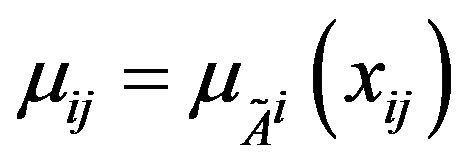 and
and 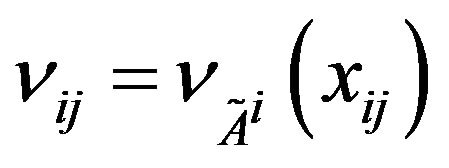 as we consider it as
as we consider it as  th element of cost matrix.
th element of cost matrix.
2.1. Triangular Intuitionistic Fuzzy Number
The definitions and operations of TIFN given by Nan, Li and Zhang [13] are stated as follows:
Definition 6: An TIFN  defined on the real number set
defined on the real number set  is an intuitionistic fuzzy set, whose membership and non-membership function are given by
is an intuitionistic fuzzy set, whose membership and non-membership function are given by

and
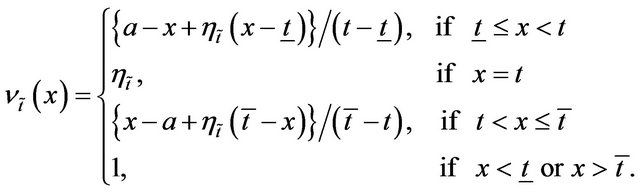
respectively, where the values  and
and 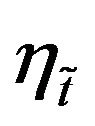 represent the maximum degree of membership and the minimum degree of non-membership, respectively, such that they satisfy the following condition:
represent the maximum degree of membership and the minimum degree of non-membership, respectively, such that they satisfy the following condition:  and
and .
.
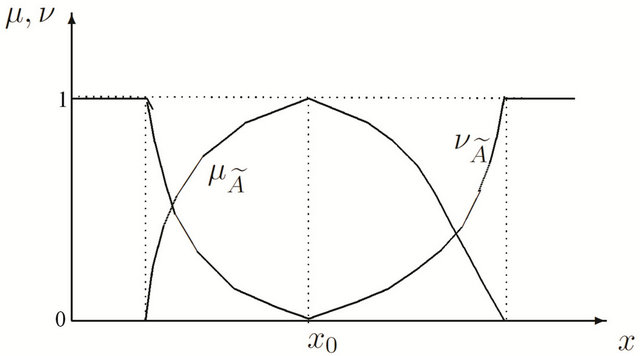
Figure 1. Membership and non-membership functions of .
.
The hesitancy degree or the degree of indeterminacy membership of the element x to the TIFN 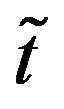 can be given as
can be given as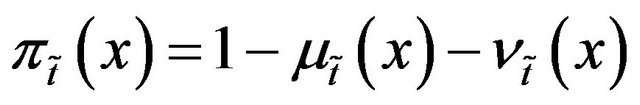 . Here
. Here 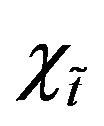 and
and 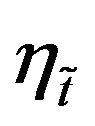
represent respectively the confidence and non-confidence levels of the TIFN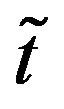 .
.
Definition 7: Let us consider two TIFNs as 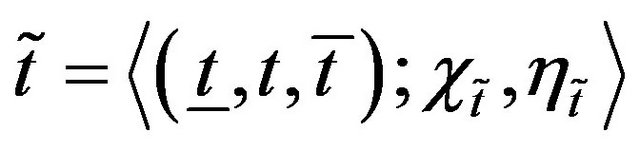 ,
, . With
. With 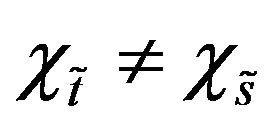 , the arithmetic operations are defined as follows:
, the arithmetic operations are defined as follows:
1)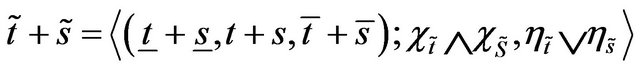 where
where  and
and  represent min and max operators respectively.
represent min and max operators respectively.
2) 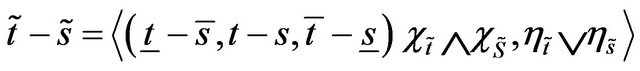
3)
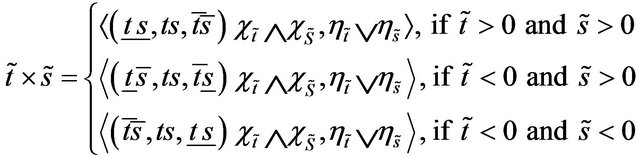
4) 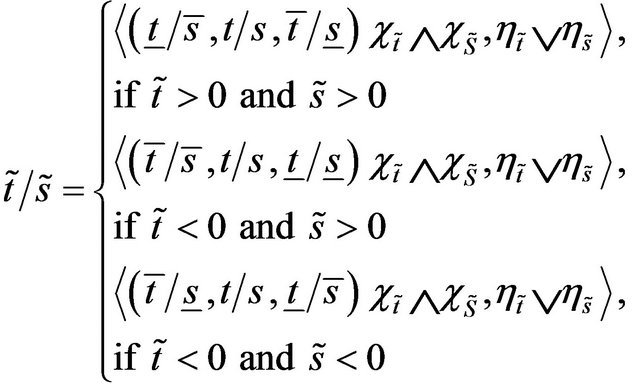
5) 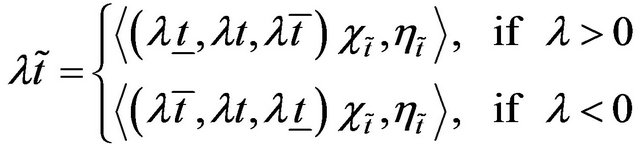
where  is any real number.
is any real number.
6) 
2.2. Cut Sets of TIFN
Definition 8: A 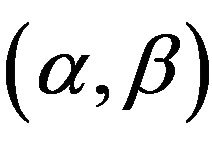 - cut set of
- cut set of 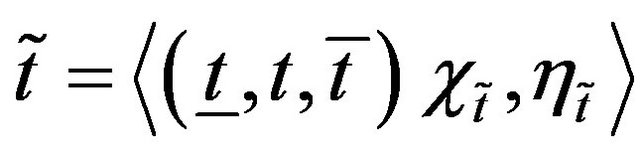 is defined over a crisp subset of
is defined over a crisp subset of  and it is given as
and it is given as
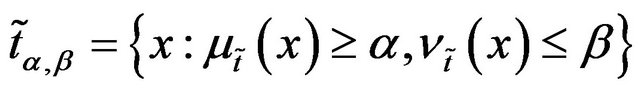 where
where 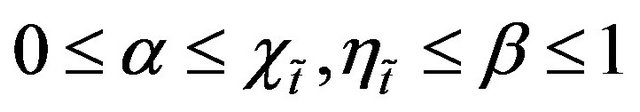 and
and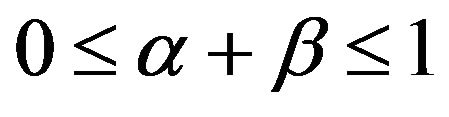 .
.
Definition 9: A 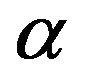 -cut set of
-cut set of 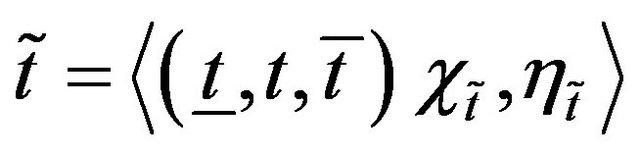 is defined over a crisp subset of
is defined over a crisp subset of  and it is given as
and it is given as . Corresponding closed interval is given as
. Corresponding closed interval is given as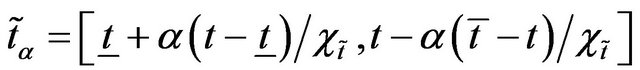 .
.
Definition 10: A  -cut set of
-cut set of  is defined over a crisp subset of
is defined over a crisp subset of  and it is given as
and it is given as
 . Corresponding closed interval is given as
. Corresponding closed interval is given as

Definition 11: Let 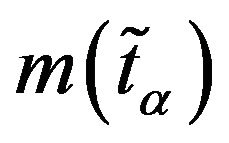 and
and 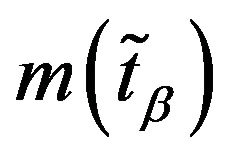 be the mean values of the intervals
be the mean values of the intervals  and
and  respectively i.e.
respectively i.e.
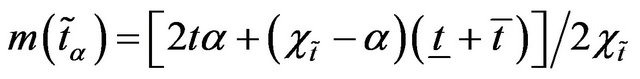
and
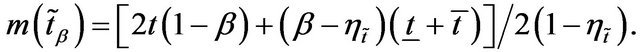
Then average index of the membership function 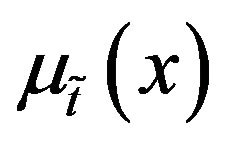 and the average index of the non-membership function
and the average index of the non-membership function 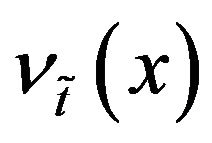 for the TIFN
for the TIFN  are defined as
are defined as


respectively. Now we will introduce deviation index of the membership function  and non-membership function
and non-membership function  for the TIFN
for the TIFN 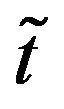 as follows.
as follows.
Definition 12: Let  and
and 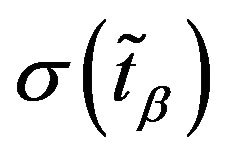 be the mean values of the intervals
be the mean values of the intervals 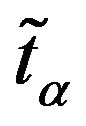 and
and 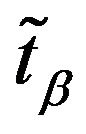 respectively i.e.
respectively i.e.

and

Then deviation index of the membership function 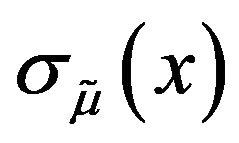 and the average index of the non-membership function
and the average index of the non-membership function 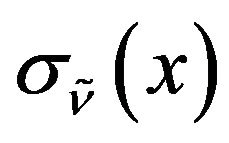 for the TIFN
for the TIFN 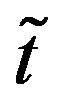 are defined as
are defined as
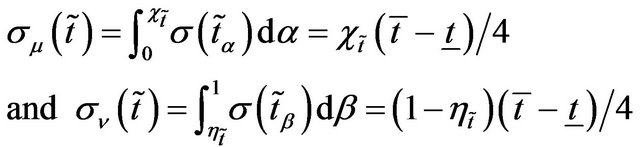
respectively. Now we will state ranking order of TIFN. In doing that one thing we should have in mind that this ranking order is not unique and it depends on the purpose concerned. Here we will define a new ranking order based on difference between  and
and 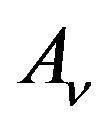 and for that purpose we will define value judgement index
and for that purpose we will define value judgement index 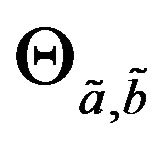 as follows Definition 13: Let
as follows Definition 13: Let 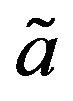 and
and  are two TIFN. The average indexes of membership functions are
are two TIFN. The average indexes of membership functions are 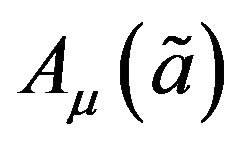 and
and 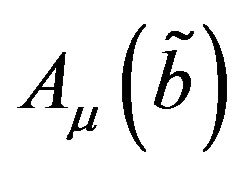 respectively and that of the non-membership function are
respectively and that of the non-membership function are  and
and 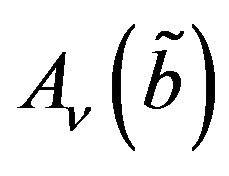 respectively.The deviation indices of membership functions are
respectively.The deviation indices of membership functions are  and
and  respectively and that of the non-membership function are
respectively and that of the non-membership function are 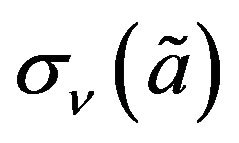 and
and 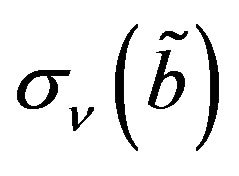 respectively. Then
respectively. Then
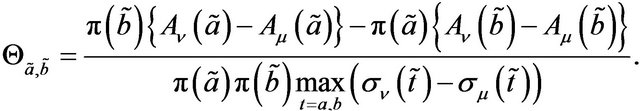 (2)
(2)
Now 1) if  then
then 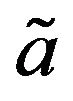 is smaller than
is smaller than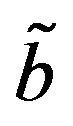 , denoted by
, denoted by 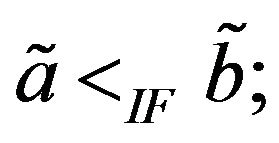
2) if  then
then .
.
Here “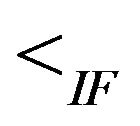 ” in intuitionistic version is equivalent to “
” in intuitionistic version is equivalent to “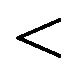 ” in real number set and has the linguistic interpretation “essentially less than”. Similarly “
” in real number set and has the linguistic interpretation “essentially less than”. Similarly “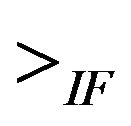 ” and “
” and “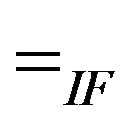 ” can be explained. For comparison of more than two TIFNs we use the notations “
” can be explained. For comparison of more than two TIFNs we use the notations “ ” and “
” and “ ” as 1)
” as 1) 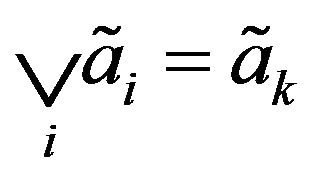 if
if  is largest among all
is largest among all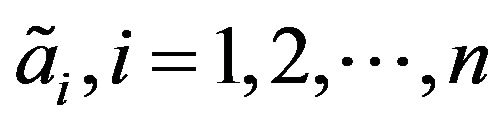 ;
;
2) 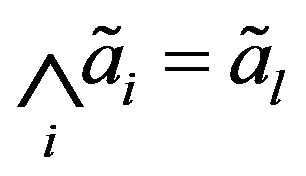 if
if  is smallest among all
is smallest among all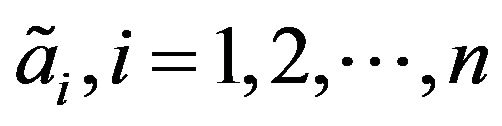 .
.
Different ranking methods [16,17] have been adopted so far considering the membership and non membership function as triangular,trapezoidal or other forms of fuzzy numbers. But it is of no use when we consider the membership and non-membership functions as acceptance and rejection degree of choice of a particular thing. In this case score function is very useful. It can be defined as follows:
Chen and Tan [18] first defined a score function  as deviation of a membership function
as deviation of a membership function 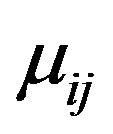 from nonmembership function
from nonmembership function 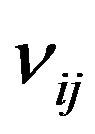 as
as
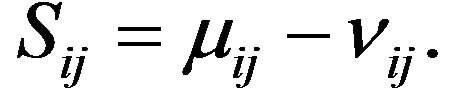 (3)
(3)
Here bigger the value of 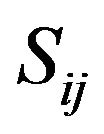 represents bigger IFN but when
represents bigger IFN but when 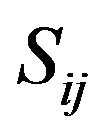 of two IFN are same then this definition does not work. So, analyzing the deficiency of this score function Hong and Chi [19] have given a precise function as
of two IFN are same then this definition does not work. So, analyzing the deficiency of this score function Hong and Chi [19] have given a precise function as
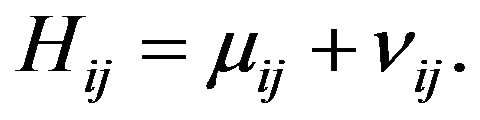 (4)
(4)
Here also bigger the value of  gives bigger IFN. Now these two scoring functions defined above have fundamental deficiency that they do not involve the uncertainty function
gives bigger IFN. Now these two scoring functions defined above have fundamental deficiency that they do not involve the uncertainty function  and this seems to be very unrealistic. Liu [20] analyzing the hesitancy degree
and this seems to be very unrealistic. Liu [20] analyzing the hesitancy degree  modified the definition as
modified the definition as
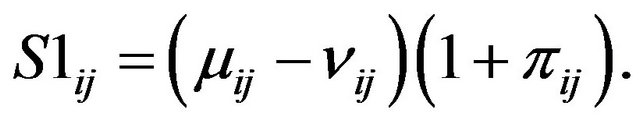 (5)
(5)
Now here we will use a very simple score function which is defined as
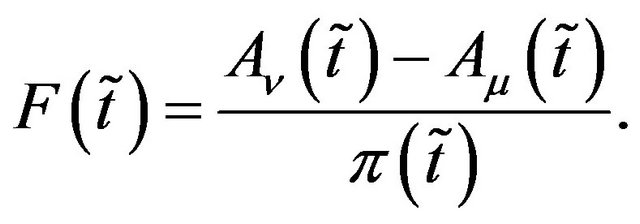 (6)
(6)
Here one thing can be observed that
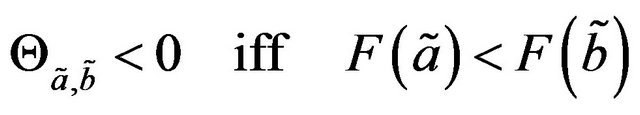 (7)
(7)
and two properties are given as 1) ;
;
2)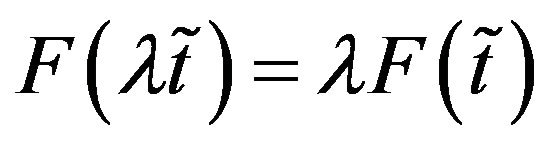 ,
,  is any real.
is any real.
3. TIFN Matrix Game
The table showing how payments should be made at the end of the game is called a pay-off matrix. If the player  has
has 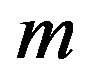 strategies available to him and the player
strategies available to him and the player 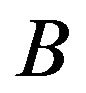 has
has 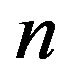 strategies available to him, then the pay-off for various strategies is represented by
strategies available to him, then the pay-off for various strategies is represented by 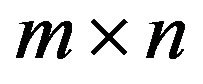 pay-off matrix. Here we consider the pay-off as TIFN
pay-off matrix. Here we consider the pay-off as TIFN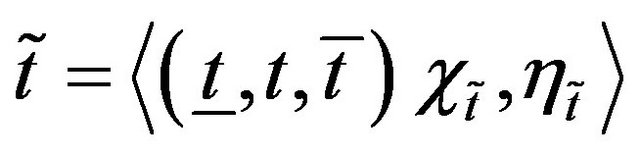 , written in the matrix form as
, written in the matrix form as
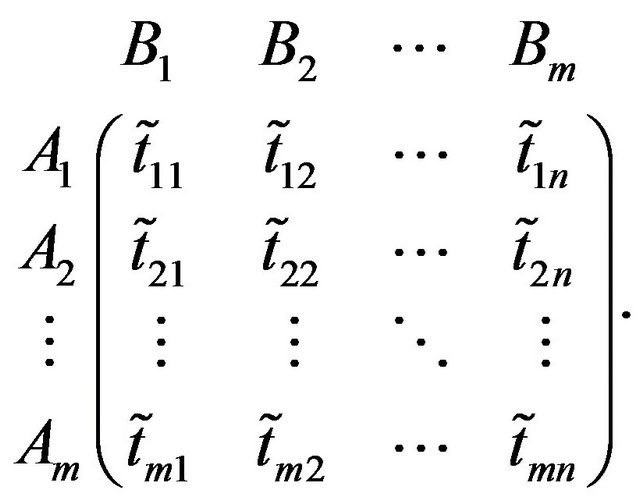
Here it is assumed that when player  chooses the strategy
chooses the strategy 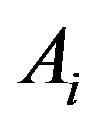 and the player
and the player 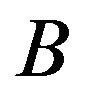 selects strategy
selects strategy  it results in a pay-off
it results in a pay-off 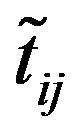 to the player
to the player .
.
Pure Strategy
Pure strategy is a decision making rule in which one particular course of action is selected. For fuzzy games the min-max principle is described by Nishizaki [2]. The course of the fuzzy game is determined by the desire of  to maximize his gain and that of restrict his loss to a minimum. Now for TIFN game,
to maximize his gain and that of restrict his loss to a minimum. Now for TIFN game,
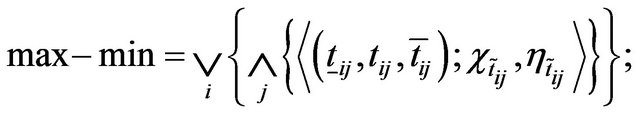 (8)
(8)
 (9)
(9)
Based on TIFN order, for such games, we define the concepts of 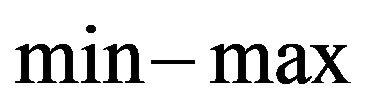 equilibrium strategies.
equilibrium strategies.
Definition 14 (Saddle Point): The concept of saddle point in classical form is introduced by Neumann [21]. The 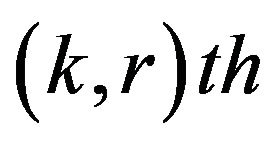 position of the pay-off matrix will be called a saddle point, if and only if,
position of the pay-off matrix will be called a saddle point, if and only if,
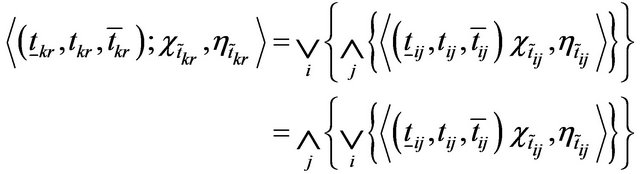
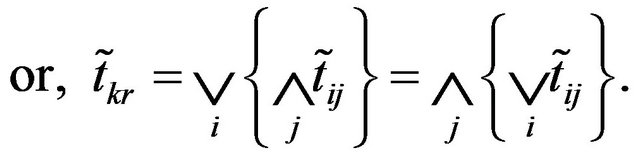 (10)
(10)
We call the position 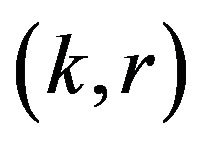 of entry a saddle point, the entry itself
of entry a saddle point, the entry itself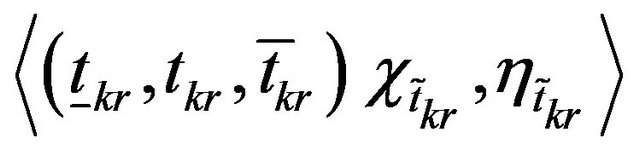 the value of the game (denoted by
the value of the game (denoted by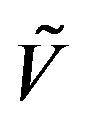 ) and the pair of pure strategies leading to it are optimal pure strategies.
) and the pair of pure strategies leading to it are optimal pure strategies.
In Nan, Li and Zhang [13] the solution method given, involve some deficiencies which can be obviated when we use the concept, given in this paper. In [13] a reasonable solution is obtained and using it, maxmin strategy and minmax strategy are defined. But maximizing the maxmin strategy and minimizing the minmax strategy does not ensure the optimality. For example, let us consider the matrix

According to the solution method defined in [13] the value of the game is
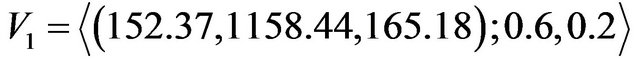
although according to the method described in this paper this matrix has a saddle point 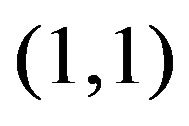 and value of the game is
and value of the game is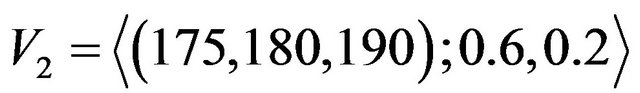 . If we consider the comparison method of two triangular intuitionistic fuzzy numbers described in [13] we will see that
. If we consider the comparison method of two triangular intuitionistic fuzzy numbers described in [13] we will see that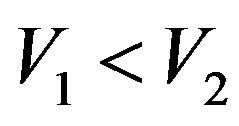 . Hence we have got better result.
. Hence we have got better result.
Definition 15: (TIFN expected pay-off ): If the mixed strategies 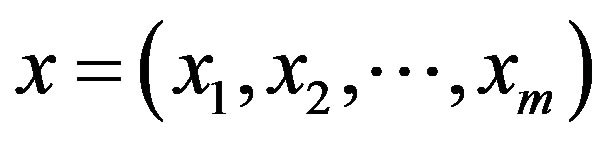 and
and 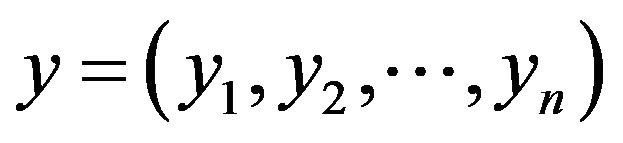 are proposed by players
are proposed by players  and
and 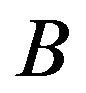 respectively, then the expected pay-off of the player
respectively, then the expected pay-off of the player  by player
by player 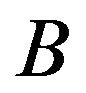 is defined by
is defined by
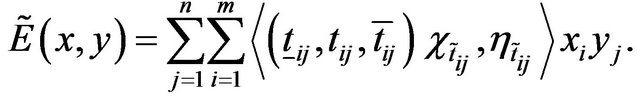 (11)
(11)
Addition and other composition rules on TIFN which we have discussed in Definition 7 are used in this definition of expected pay-off (11). In such a situation, player  chooses
chooses 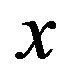 so as to maximize his expectation and player
so as to maximize his expectation and player  chooses
chooses 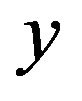 so as to minimize player
so as to minimize player ’s maximum expectation and mathematically we write
’s maximum expectation and mathematically we write
 (12)
(12)
where  is called strategic saddle point of the game and
is called strategic saddle point of the game and 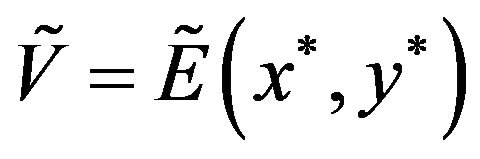 is the value of the game.
is the value of the game.
Theorem 1: If a pay-off matrix with elements as TIFN has saddle point  and
and  is the value of the game then the pay-off matrix obtained after defuzzification with the help of score function
is the value of the game then the pay-off matrix obtained after defuzzification with the help of score function 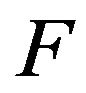 has also saddle point
has also saddle point 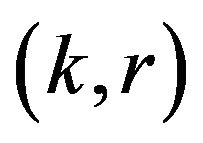 and
and  is the value of the game.
is the value of the game.
Proof: If  be the saddle point of the pay-off matrix and
be the saddle point of the pay-off matrix and 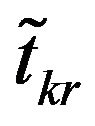 is the value of the game then
is the value of the game then

Now using the Equations (6) and (1) we have

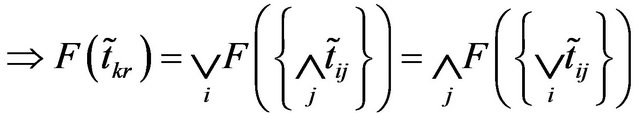
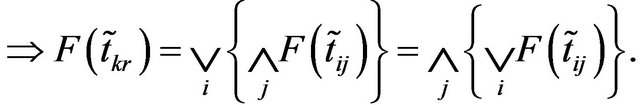
Therefore, 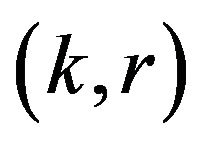 is also the saddle point of the defuzzified pay-off matrix.
is also the saddle point of the defuzzified pay-off matrix. 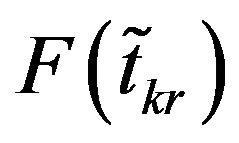 is the value of the game. Hence the theorem.
is the value of the game. Hence the theorem.
Theorem 2: If 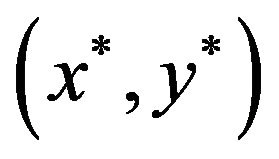 be the strategic solution of the pay-off matrix with mixed strategies then
be the strategic solution of the pay-off matrix with mixed strategies then  is also the solution of the pay-off matrix after defuzzification by score function
is also the solution of the pay-off matrix after defuzzification by score function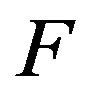 .
.
Proof: Let 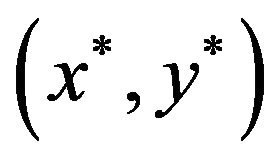 be the solution of the pay-off matrix then
be the solution of the pay-off matrix then
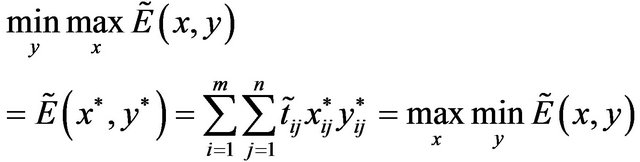
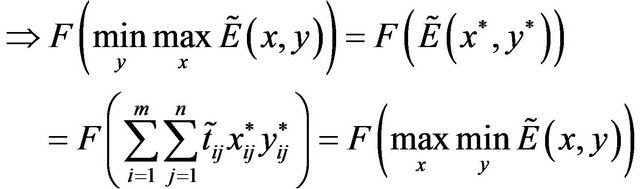

Therefore,  is also a strategic solution of the defuzzified pay-off matrix and value of the game is
is also a strategic solution of the defuzzified pay-off matrix and value of the game is
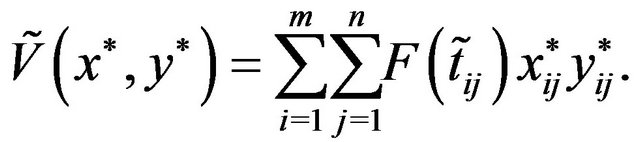 Hence the theorem.
Hence the theorem.
4. An Application to Voting Share Problem
Suppose that there is an election where two major political parties A and B take part and total number of voters in that region is constant. It means that the increase in percentage of voters for one political party results in the same for the other political party. Suppose  has two strategies as
has two strategies as
 Giving importance in door to door campaigning and carrying their ideology and issues to people.
Giving importance in door to door campaigning and carrying their ideology and issues to people.
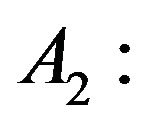 Co-operating with other small political parties to reduce secured votes of the opposition.
Co-operating with other small political parties to reduce secured votes of the opposition.
At the same time 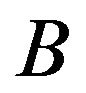 takes two strategies:
takes two strategies:
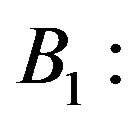 campaigning by celebrities and big rallies.
campaigning by celebrities and big rallies.
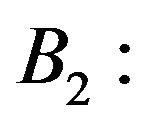 Making lot of promises to the people.
Making lot of promises to the people.
Now the chief voting agents can not say exactly about the voting percentage but they have a certain confidence level. Still there is some hesitancy in that confidence level due to bad weather forecast. In such win-win situation we may consider the pay-offs as TIFN and the matrix is given as

Here  represents that when
represents that when  plays the strategy
plays the strategy  and
and 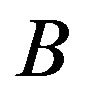 plays the strategy
plays the strategy 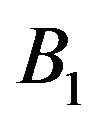 then resulting expected votes in favor of
then resulting expected votes in favor of  is approximately
is approximately  lakhs with lower bound of
lakhs with lower bound of  lakhs and upper bound of
lakhs and upper bound of  lakhs. The maximum confidence level and minimum non-confidence level of the Chief election agent of
lakhs. The maximum confidence level and minimum non-confidence level of the Chief election agent of  are
are 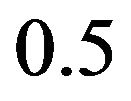 and
and  respectively.
respectively.
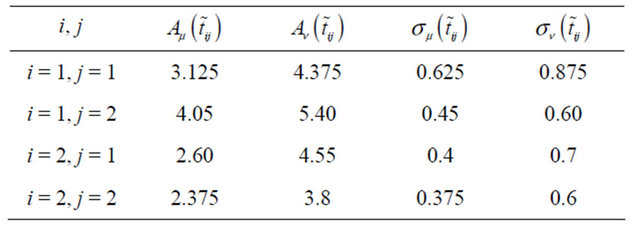
Now, let us consider the elements of the pay-off matrix as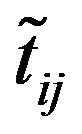 . Then using the ranking order we can get Table 1. Using Equation (5) we get the crisp matrix as
. Then using the ranking order we can get Table 1. Using Equation (5) we get the crisp matrix as
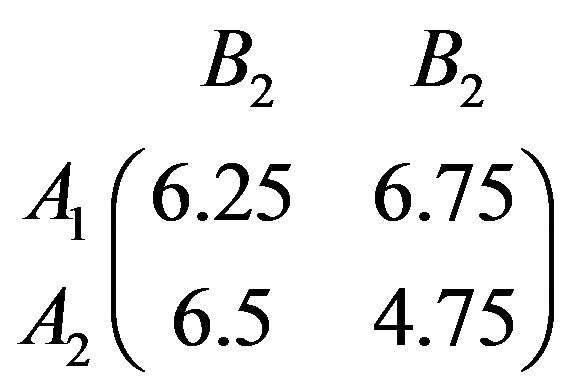
Since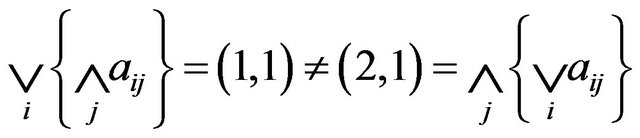 , saddle point does not exist. If we would use
, saddle point does not exist. If we would use  for comparing the TIFN of original pay-off matrix we would get the same result. So,using the mixed strategy method for crisp payoff matrix we get
for comparing the TIFN of original pay-off matrix we would get the same result. So,using the mixed strategy method for crisp payoff matrix we get ,
, 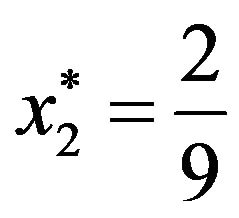 which are the probabilities with which player A plays the strategies
which are the probabilities with which player A plays the strategies  and
and
 . Similarly,
. Similarly, 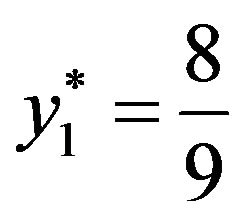 and
and 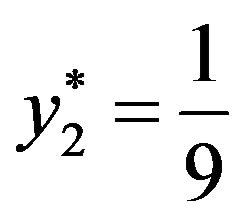 are the probabilities with which player B plays with strategies
are the probabilities with which player B plays with strategies 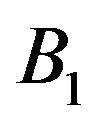 and
and . The value of the game is
. The value of the game is 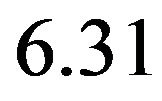 which gives optimal score in favor of player
which gives optimal score in favor of player 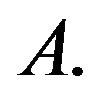 Since we would get same optimal strategies for player
Since we would get same optimal strategies for player  and player
and player 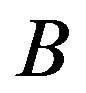 if we would use the original pay-off matrix as evident from Theorem 2, the value of the game as a TIFN is given as
if we would use the original pay-off matrix as evident from Theorem 2, the value of the game as a TIFN is given as
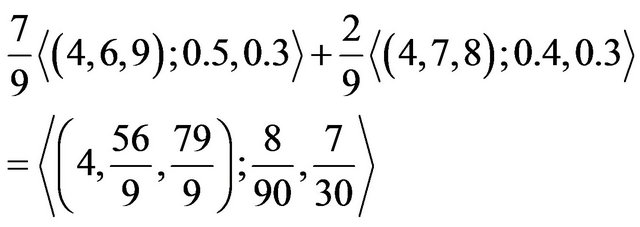
which actually represents that the expected optimal votes for player  is
is 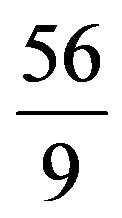 lakhs which could be as low as 4 lakh and reach as high as
lakhs which could be as low as 4 lakh and reach as high as 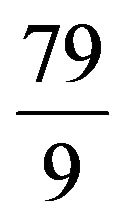 lakhs. The maximum confidence level and minimum non-confidence level for the decision maker are
lakhs. The maximum confidence level and minimum non-confidence level for the decision maker are 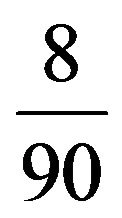 and
and  respectively.
respectively.
Results and Discussion
This result actually represents that the expected optimal votes for player  is
is 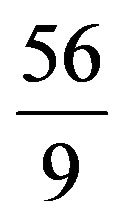 lakhs which could be as low as 4 lakh and reach as high as
lakhs which could be as low as 4 lakh and reach as high as 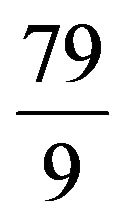 lakhs. The maximum confidence level and minimum non-confidence level for
lakhs. The maximum confidence level and minimum non-confidence level for
Table 1. The computation results.
the decision maker are 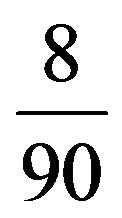 and
and  respectively. Unlike [13], in this paper, we didn’t go for the reasonable solution and instead, we tried to reach to the optimality with the help of a crisp pay off matrix. The reasonable solution [13] does not confirm the optimality but the theorems 1 and 2 support that the optimality exist when we use this method.
respectively. Unlike [13], in this paper, we didn’t go for the reasonable solution and instead, we tried to reach to the optimality with the help of a crisp pay off matrix. The reasonable solution [13] does not confirm the optimality but the theorems 1 and 2 support that the optimality exist when we use this method.
5. Conclusion
In this paper,we have used TIFN as elements of pay-off matrix. As a result we have considered here players? preference information in terms of support, opposition and neutralization and also his confidence and nonconfidence level about the approximation. Using the definitions and operations of TIFN we have described a ranking order based on the definition of value judgement index. Then we have described score function to defuzzify the matrix game and made a comparative study on scoring function approach and an IF approach in voting share problem. The merit of this methodology is that it obtains a deterministic solution of a matrix game with IF pay-off. There is a scope to apply such a methodology in other conflicting interest problems.
REFERENCES
- I. Nishizaki and M. Sakawa, “Equilibrium Solutions for Multiobjective Bimatrix Games Incorporating Fuzzy Goals,” Journal of Optimization Theory and Applications, Vol. 86, No. 2, 1995, pp. 433-457. doi:10.1007/BF02192089
- I. Nishizaki and M. Sakawa, “Max-Min Solution for Fuzzy Multiobjective Matrix Games,” Fuzzy Sets and Systems, Vol. 61, No. 1, 1994, pp. 265-275.
- P. K. Nayak and M. Pal, “Solution of Rectangular Fuzzy Games,” OPSEARCH, Vol. 44, No. 3, 2009, pp. 211-226.
- P. K. Nayak and M. Pal, “Solution of Interval Games Using Graphical Method,” Tamsui Oxford Journal of Mathematical Sciences, Vol. 22, No. 1, 2006, pp. 95-115.
- P. K. Nayak and M. Pal, “Linear Programming Technique to Solve Two Person Matrix Games with Interval PayOffs,” Asia-Pacific Journal of Operational Research, Vol. 26, No. 2, 2009, pp. 285-305. doi:10.1142/S0217595909002201
- A. L. Narayan, A. R. Meenakshi and A. M. S. Ramasamy, “Fuzzy Games,” The Journal of Fuzzy Mathematics, Vol. 10, 2002, pp. 817-829.
- R. E. Moore, “Method and Application of Interval Analysis,” Society for Industrial and Applied Mathematics (SIAM), Philadelphia, 1979. doi:10.1137/1.9781611970906
- H.-J. Zimmermann, “Fuzzy Mathematical Programming,” Computer Operational Research, Vol. 10, No. 4, 1983, pp. 291-298. doi:10.1016/0305-0548(83)90004-7
- K. Atanassov, “Intuitionistic Fuzzy Sets,” Fuzzy Sets and Systems, Vol. 20, No. 1, 1986, pp. 87-96. doi:10.1016/S0165-0114(86)80034-3
- K. T. Atanassov, “Ideas for Intuitionistic Fuzzy Equations, Inequalities and Optimization,” Notes on Intuitionistic Fuzzy Sets, Vol. 1, No. 1, 1995, pp. 17-24.
- D. F. Li and J. X. Nan, “A Nonlinear Programming Approach to Matrix Games with Payoffs of Atanassov’s Intuitionistic Fuzzy Sets,” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, Vol. 17, No. 4, 2009, pp. 585-607.
- M. R. Seikh, M. Pal and P. K. Nayak, “Application of Triangular Intuitionistic Fuzzy Numbers in Bi-Matrix Games,” International Journal of Pure and Applied Mathematics, Vol. 79, No. 2, 2012, pp. 235-247.
- J.-X. Nan, D.-F. Li and M.-J. Zhang, “A Lexicographic Method for Matrix Games with Payoffs of Triangular Intuitionistic Fuzzy Numbers,” International Journal of Computational Intelligence Systems, Vol. 3, No. 3, 2010, pp. 280-289. doi:10.2991/ijcis.2010.3.3.4
- K. Atanassov, “Intuitionistic Fuzzy Sets: Theory and Applications,” Physica-Verlag, Berlin, 1999. doi:10.1007/978-3-7908-1870-3
- M. R. Seikh, M. Pal and P. K. Nayak, “Notes on Triangular Intuitionistic Fuzzy Numbers,” International Journal Mathematics in Operation Research, 2012.
- G. S. Mahapatra and T. K. Roy, “Reliability Evaluation Using Triangular Intuitionistic Fuzzy Numbers Arithmetic Operations,” International Journal of Computational and Mathematical Sciences, Vol. 3, No. 5, 2009, pp. 225- 231.
- H. B. Mitchell, “Ranking Intuitionistic Fuzzy Numbers,” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, Vol. 12, No. 3, 2004, pp. 377-386. doi:10.1142/S0218488504002886
- S.-M. Chen and J.-M. Tan, “Handling Multicriteria Fuzzy Decision Making Problems Based on Vague Set Theory,” Fuzzy Sets and Systems, Vol. 67, No. 2, 1994, pp. 163- 172. doi:10.1016/0165-0114(94)90084-1
- D. H. Hong and C.-H. Choi, “Multicriteria Fuzzy Decision Making Problems Based on Vague Set Theory,” Fuzzy Sets and Systems, Vol. 144, No. 1, 2000, pp. 103- 113.
- H. W. Liu, “Vague Set Methods of Multicriteria Fuzzy Decision Making,” System Engineering, Theory and Practice, Vol. 5, No. 5, 2004, pp. 214-220.
- J. V. Neumann and O. Morgenstern, “Theory of Games and Economic Behaviour,” Princeton University Press, Princeton, 1947.
NOTES
*Corresponding author.

