Graphene
Vol.06 No.03(2017), Article ID:77592,13 pages
10.4236/graphene.2017.63006
Polycyclic Aromatic Hydrocarbon Molecule-Surface Binding Energies in Site Specific Graphene Bilayer Nanopores: A Puzzle-ene Force Field Calculation
Thomas R. Rybolt, Claire B. Black
Department of Chemistry and Physics, University of Tennessee at Chattanooga, Chattanooga, USA

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 12, 2017; Accepted: July 9, 2017; Published: July 13, 2017
ABSTRACT
Two-dimensional molecular recognition studies of the six polyaromatic hydrocarbons that can be formed from the combination of four benzene rings: tetracene, pyrene, 1,2-benzanthracene, 3,4-benzphenanthrene, triphenylene, and chrysene were explored for each of these six molecules interacting with six different graphene layer site-specific nanopores. Computational studies were done for the gas phase adsorption on single layer graphene, bilayer graphene, and six molecule-specific graphene bilayer nanopores. Molecular mechanics MM2 parameters have been shown previously to provide good comparisons to experimental adsorption energies for aromatic hydrocarbons adsorption on graphitic surfaces. These binding energies are dominated by van der Waals forces. Just as a jigsaw puzzle hole can accommodate only a specific piece, two-dimensional shape specific sites were created in the top layer of a graphene bilayer to match each one of the six adsorbate molecules. The purpose of this study was to examine the molecular recognition possibilities of site specific adsorption in these simple two-dimensional nanopores based on dispersion forces and molecular shape. For example, triphenylene has a calculated surface binding energy of 24.5 kcal/mol on the graphene bilayer and 30.2 kcal/mol in its own site specific pore. The interaction energy of this molecule in the other five sites ranged from 17.6 to 23.8 kcal/mol. All the molecules tetracene, pyrene, 1,2-benzanthracene, triphenylene and chrysene had higher binding energies in their matched molecule bilayer sites than on either single or double layer graphene. In addition, each one of these five molecules had a stronger binding in their own shape specific (puzzle-ene) site than any of the other molecular sites. The results suggest that two-dimensional molecular recognition based on shape specific pores may allow selectivity useful for applications such as sensors, separations, nanofabrication, or information storage.
Keywords:
Molecule-Graphene Interaction, Molecular Mechanics, Adsorption Energy, Binding Energy on Graphene, Polycyclic Aromatic Hydrocarbons, Two-Dimensional Molecular Recognition

1. Introduction
The role of three-dimensional recognition through covalent and noncovalent interactions and the subsequent transformations of molecular structures are key features of enzymatic and other biological nanosystems. We wish to explore an extremely simple system of molecular recognition by allowing only for nonco- valent van der Waals forces within a two-dimensional bilayer graphene surface and a “carved out” site shaped to match one of six target polyaromatic hydro- carbon (PAH) molecules. When a traditional two-dimensional jigsaw puzzle is complete except for the last piece, there is a unique site that can “recognize” or fit only a specific piece. By analogy, we wish to explore the computational fitting of a set of flat PAH molecules into sites where each site is designed to specifically fit one molecule.
Single and bilayer structures of graphene exhibit unique and useful properties [1] [2] . Single and bilayer graphene can function as molecular sensors as demonstrated by practical applications [3] [4] [5] [6] [7] and theoretical calcula- tions [8] [9] .
In prior work the ability to predict single and multilayer graphene binding energies for a variety of organic molecules was demonstrated using MM2 mole- cular mechanics parameters [10] . MM2 parameters have been used to estimate the binding energies of organic molecules on carbon surfaces [11] [12] [13] . Force field calculations do not reference electronic behavior but can determine minimum energies and optimized molecular geometries [14] .
Organic molecule-graphite interaction energies have been determined from thermal programmed desorption (TPD) and gas-solid chromatography (GSC). TPD experiments involve multilayer or monolayer desorption and include mo- lecule-molecule interactions [11] . However, many GSC determinations are based on low coverage, Henry’s law adsorption for isolated molecule-surface interac- tions. In prior work experimental energies were tabulated and molecular me- chanics MM2 calculations were used to compute molecule-graphite binding energies Ecal* for 118 organic molecules [10] . Also MM2 parameters and molecular mechanics calculations have been used to estimate molecule surface interaction energies on models of a flat plate surface, a parallel plate pore surface, and a double parallel plate (box-like) pore [15] .
The polycyclic benzenoid hydrocarbons that were considered for this analysis were created from among seven possible structures of four fused benzene rings. The molecules examined were tetracene, pyrene, 1,2-benzanthracene, 3,4-benz- phenanthrene, triphenylene and chrysene (see Figure 1). A seventh possible four
Figure 1. The six polycyclic aromatic hydrocarbons formed from four benzene rings in various fused combinations have shapes that roughly resemble the letter used for each molecule: tetracene (I), pyrene (O), 1,2-benzanthracene (r), 3,4-benzphenanthrene (U), triphenylene (Y) and chrysene (Z). Calculations were based on molecular mechanics using MM2 parameters.
ring molecule, 10H-benzo[de]anthracene, was not used due to its lack of aroma- ticity Two dimensional site-specific nanopores were created for each of the six molecules used (see Figure 2).
There is ongoing interest in the interaction of PAHs and other adsorbates on two-dimensional surfaces. The adsorption of PAHs on graphene and graphene oxide nanosheets has been characterized by a variety of spectroscopic and visua- lization techniques including XPS, FTIR, Raman, SEM, and TEM with stronger adsorption of PAHs to graphene than graphene oxide observed [16] . Scanning tunneling microscopy (STM) imaging of the PAHs benzene, coronene, and hexabenzocoronene on a graphene layer have resulted in images of molecular struc-
Figure 2. Site specific nanopores were created for each molecular shape by first removing carbons in the graphene layer that match the carbon atoms in the target molecule, by second removing surface carbons in locations analogous to the hydrogens in the molecule, and by third removing graphene layer carbons bonded to the previously removed carbons in step two. The nanopores are formed in one layer of a bilayer structure. Only the center portion of the layer around the two-dimensional opening is shown. To make it easier to view, not all 432 rings in a graphene layer are shown, and the bottom layer of graphene is not shown. Calculations were based on molecular mechanics using MM2 parameters.
tures and self-assembles of molecules [17] . Molecular superstructures deter- mined by intermolecular interactions on a surface with templated guided growth have been imaged by scanning tunneling microscopy (STM) [18] .
2. Theory
A molecular mechanics MM2 force field calculation for the energy required for desorption is
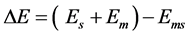 (1)
(1)
where Em is the energy of an isolated gas phase molecule, Es is the energy of the isolated surface adsorbent material, and Ems is the energy of the molecule and solid surface system where the molecule on the surface represents the adsorbed state [10] . The adsorption energy is simply the negative value of ∆E as written above. Either a positive desorption energy or negative adsorption energy repre- sent favorable binding energy of the molecule in its attraction to the surface. All binding energies in this work are reported as positive values.
In calculations for graphite 90% or more of the van der Waals (vdW) interac- tion is due to the first layer, 9% or less due to the second layer and only 1% or less due to the third layer [11] . Molecular energy calculated from molecular me- chanics is a sum of covalent and noncovalent energies. In this work all binding energies are reported as positive values and the van der Waals interaction energy, EvdW, from molecular mechanics is the primary contributor to molecule-sur- face binding.
Previously binding energies for DNA/RNA nucleobases adsorbed graphene were calculated [19] . These force field MM2 calculations gave values between those reported from Moller-Plesset perturbation theory which were reported to overestimate and the values from density functional theory (DFT) which were reported to underestimate the values [19] .
MM2 parameters used to calculate molecule-surface binding energies compa- red well to experimental values obtained from gas-solid chromatography (GSC) for isolated molecule physical adsorption. Considering molecule-molecule near- est neighbor interactions, calculated monolayer coverage binding energies also compared well to thermal program desorption (TPD) experiments. TPD expe- riments and MM2 calculations for monolayer desorption gave 0.50 and 0.52, 0.72 and 0.71, and 1.41 and 1.47 eV for benzene, o-dichlorobenzene, and coro- nene, respectively [11] .
3. Analysis
Initially molecular mechanics MM2 and MM3 calculations were performed with Scigress software (Fujitsu) with the geometry optimized in mechanics using augmented MM2 and MM3 parameters. The graphene model surface consisted of one layer of 432 benzene rings with no hydrogen atoms.
Calculations were performed to determine the energy required to separate the molecule from the surface. For neutral organic molecules on a graphene surface, vdW changes dominate. A molecule placed on a graphene surface closer than the expected optimal distance and oriented with benzene rings of the molecule di- rectly above the benzene rings of the surface layer of graphene is pushed to the optimal distance from the surface. The isolated molecule and isolated surface structure energies were determined and Equation (1) used to find ∆E.
Before any calculations regarding the two-dimensional nanopores were performed, we explored some of the parameter options for MM2 and MM3 molecular mechanics. The parameters that were investigated were: MM2 or MM3, effective of increasing layers of graphene, and vdW cutoff value.
Calculations using Equation (1) gave values for benzene-surface interactions for MM2 2-layer and 3-layer graphene of 9.4 and 9.4 kcal/mol and interactions for MM3 2-layer and 3-layer of 10.6 and 10.8 kcal/mol, respectively. These values may be compared to an experimental datum based on gas-solid chromatography that found that the experimental adsorption energy, E*, of benzene on graphite was 4474K or 8.9 kcal/mol [20] .
A comparison to computed values for MM2 2-layer and 3-layer graphene gave results that were both higher than the experimental value by 6.0%. MM3 2-layer and 3-layer graphene gave results that were higher than the experimental value by 19% and 21%, respectively. This observation along with prior results utilizing MM2 to calculate the binding energies on graphitized thermal carbon black (GTCB) for a data set of 118 organic molecules [10] showed that MM2 was quite effective in calculating binding energies. In prior work, modification had to be made for MM2 binding energy values involving sp3 carbon atoms but values for aromatic sp2 carbon structure and other heteroatoms gave appropriate values. Without modification MM2 was especially effective in obtaining the carbon surface binding energy values of rigid molecules such as polyaromatic hydrocar- bons.
The other parameter that was explored was the van der Waals cutoff value. The normal default vdW cutoff value of 9 angstrom (0.9 nm). This distance means that the van der Waals interaction will be considered in calculating energies if the interactions occur within 9Å internuclei separation. To determine if this distance was adequate, calculations were performed using 1, 2, 4, 6 and 8 layers of 432-ring graphene with Van der Waals cutoff distances varied between 7, 8, 9, 12 and 15Å. After all calculations were performed it was deemed that 9Å would be an adequate vdW cutoff value. Using a cutoff value of 9Å on 1 layer of graphene yielded on average only a few percent error when compared to expe- rimental values [10] .
Once the parameters for calculations were chosen, a standard procedure for creating the flat nanopores within one graphene layer of the bilayer structure was used. The pore creation approach can be described for benzene. The first step is to remove six carbons in the shape of a benzene ring from the center of the top layer of a two-layer 432-ring graphene surface. Second six more surface carbons are removed in locations analogous to the hydrogens in the benzene. Third, each surface carbon that is attached to the previously removed carbons must also be removed and this gives 12 more removed atoms. Thus a flat pore for a single benzene molecule requires the removal of 24 carbon atoms from a graphene layer to create a suitable molecule specific shape site.
Once a method was established for creating site-specific nanopores, it was necessary to decide what molecules would be used, create them, and create site-specific nanopores for each one. As mentioned previously, it was decided that the molecules to be used would be the six possible arrangements of four benzene rings that remain aromatic. 10H-benzo[de]anthracene, was not used due to its lack of aromaticity. The six molecules used were tetracene (molecule I), pyrene (molecule O), 1,2-benzanthracene (molecule r), 3,4-benzphenanth- rene (molecule U), triphenylene (molecule Y) and chrysene (molecule Z). Each of these molecules were abbreviated by a letter that generally resembled their shape (see Figure 1).
Site-specific nanopores were created for each molecule (see Figure 2). Each one layer deep nanopore was abbreviated according to the letter of the molecule that fit in the nanopore. These nanopores were created as previously described in the approach for benzene. The overall structure consisted of two graphene layers, with the top layer having the necessary carbons removed from a 432 ring graphene and the bottom layer being a complete of 432-ring graphene layer. In the interest of easier visualization Figure 2 shows only the center portion of the layer around the two-dimensional opening and not all 432 rings in the structure. Also to make it easier to view, the bottom layer of graphene is not shown.
Each two-dimensional site was large enough so that when mechanics calculations were run the entire molecule stayed in plane with the top graphene layer, but not so large that there was extra space between the molecule and the graphene layer when viewed in space-filling mode (see Figure 3). If the surface pore was too small or did not fit well then then a molecule initially placed into the open area could be pushed at least partially out of the plane of the top graphene layer and the interaction energy significantly reduced due to this poor fit or lack of “molecular recognition” (see Figure 4).
Figure 3. Molecule Y (triphenylene) above the surface and then after it adsorbs and fits into site?Y.
Figure 4. Molecule Z (chrysene) with a poor fit into site?O where only a portion of the molecule fits into the site. This poor fit leads to a lower binding energy and “recognition” that this molecule is not molecule O which would have the optimal site binding.
4. Results and Discussion
After parameters were chosen, molecules selected, and the molecule site-specific nanopores created, MM2 calculations were run to determine desorption binding energies, ∆E, which as noted earlier were primarily due to vdW interactions. ∆E values were found for each of the six molecules on both the single layer graphene and unmodified bilayer graphene (see Table 1). Each graphene layer consisted of 432 carbon rings. Also ∆E values were obtained for each molecule placed into its site-specific nanopore (see Table 1).
Molecule U goes out plane and so is not flat and therefore behaves differently than the other five molecules. For molecule U the site specific binding shows an increase (more favorable or stronger binding energy) of 14% over the single layer and 8% over the bilayer interaction. However, the other five molecules that maintain their planarity I, O, r, Y, and Z have an average of increase of ∆E of 34% over their single layer values and 25% over their bilayer values. So the one layer thick, shallow nanocavity does significantly enhance the molecule-surface interaction.
Each of the six molecules were placed one at a time into each of the six possible adsorption sites. Obviously one site was specific for the molecule and other five sites were not specific to that molecule. Desorption energies, ∆E values, were determined for each molecule in each of the six sites (see Table 2). Note that for
Table 1. Comparison of desorption binding energy, ∆E (kcal/mol), for each of the six PAH molecules in a two-dimensional molecule-specific nanopore, on a single layer graphene surface, and on a two-layer graphene surface.
Table 2. Comparison of desorption binding energy, ∆E (kcal/mol), for each of the six PAH molecules in each of the two-dimensional molecule-specific nanopore sites.
molecules I, O, r, Y, and Z the desorption (or binding) energies for each molecule in non-specific surface sites were clearly lower than the site specific ∆E. These results indicated that each of these five planar molecules given thermodynamic equilibrium will preferentially distribute primarily to their site-specific nanopore over any other non-specific nanopore or over a flat uniform surface.
Molecule U was an exception to the above observation. Molecule U in site U had a stronger binding energy than sites I and Y. However, molecule U had a smaller ∆E for site U than molecule U in sites O, r, and Z. So this molecule binds more favorable in sites O, r, and Z.
In addition to working with site-specific nanopores, a method was developed for estimating adsorption energy on a single layer graphene surface. This was done by finding the energy per carbon and the energy per benzene for each of the six aromatic molecules adsorbed onto a single layer flat graphene surface. For the five planar molecules I, O, r, Y, and Z, it was observed that the desorp- tion energy per carbon atom (hydrogens not counted) is about 1.26 kcal/mol (55 meV) and per effective benzene ring it was determined to be 7.56 kcal/mol. Ef- fective benzene rings, means that each carbon atom can only be counted toward one ring so the effective number of rings for the molecules I, O, r, Y, and Z was 3, 2.67, 3, 3, and 3, respectively. Molecule U is 1.15 kcal/mol or slightly less per carbon atom because of its nonplanarity and poor fit.
Bjork et al. had observed for a variety of PAHs a general increase in binding energy per carbon atom as the PAH became smaller and thus the number of hydrogen atoms was greater relative to the number of carbon atoms [21] . So for example, the energy per carbon increased from coronene to naphthalene to benzene. They examined the adsorption of PAHs and other π-conjugated systems by a van der Waals density functional (vdw-DF), three semiempirical corrections to DFT, and two empirical force fields [21] . They compared this variety of computational methods and these methods were generally consistent with the experimental reported values. Our value of 55 meV per carbon atom would be at the low end of their computational methods reported but within the observed experimental range for coronene.
Our simple additivity method also was compared for the desorption energy of coronene C24H12. It was predicted using energy per carbon or per effective number of rings to be 30.24 kcal/mol. The reported experimental desorption energy was 32.30 kcal/mol [22] . An important difference, however, between the calculated and experimental energies is that the experimental energy includes adsorbate interactions at monolayer coverage, while our calculated energy was for a single molecule on the surface. Therefore, we expect that the coronene value should be higher for the experiment than our predicted value.
The binding energy of an adsorbate molecule is determined by molecule size, molecule orientation, and the nature of surface. For organic molecules adsorbed on graphitic surfaces, van der Waals forces tend to dominate the physical adsorption. Larger more polarizable atoms tend to increase vdW forces and thus increase the binding energy. As shown in Table 1, the ∆E value for molecule-O is lower than the others because it only has 16 carbons unlike the others molecules that all are C18H12. Molecule-U is lower because it tends to be nonplanar and thus has poorer surface contact.
5. Conclusions
The weakness of noncovalent vdW interactions presents a general challenge for more exact quantum mechanical methods and density functional theory (DFT) calculations. Tauer and Sherrill examined π-π interactions for benzene dimers and trimmers and found that MP2 calculations with small basis sets tended to have cancelling errors. By allowing these errors to offset each other they were able to find interaction energies close, few tenths of kcal/mol, of a complete basis set couple cluster CCSD(T) limit [23] . For large surface areas, and larger or multiple molecules, force field calculations can provide a quick and useful estimates of molecule-surface binding energies.
Simpler non-quantum mechanical calculations based on classical molecular mechanics continue to be of use to estimate molecule-surface binding energies based on weaker dispersion forces. This molecular mechanics approach does not provide any electronic details but it is a useful, computationally simple approach to study molecule interactions on carbon surfaces and should be helpful to predict how strongly various molecules may be held on surfaces or in vdW binding sites.
Molecular recognition is of vital importance in biological nanosystems whether it is a molecular substrate fitting into an enzyme active site or base pairing in DNA [24] . In these and many other cases, recognition means favorable interaction or binding. Small difference in binding preferences can give rise to large differences in population differences through the Boltzmann factor exp(−Ediff/RT) where Ediff is the energy difference between molecular binding energy in two different sites.
For example, molecule I enters into site-I with a binding energy of 31.1 kcal/mol (130 kJ/mol). The next highest binding for molecule I is in site-Z at 26.7 (112 kJ/mol). At 298 K using Ediff = 18 kJ/mol and the Boltzmann factor gives a population difference of molecule I in site-I relative to site-Z of about a 1400 to 1 ratio. The least interaction energy for molecule I is for site-O at 19.9 kcal/mol (83.3 kJ/mol). At 298 K using Ediff = 46.7 kJ/mol and the Boltzmann factor gives a population difference of molecule I in site-I relative to site-O of about a 1.5 × 108 to 1 ratio. This represents effective molecular recognition.
Referring to Table 2, it is observed that with the exception of molecule U, the molecule specific site is favored. For example, if molecule Y in site-Y is taken as a reference then the binding of molecule Y is less favorable in sites I, O, r, and Z by 12.6, 11.9, 10.8, and 10.1 kcal/mol, or (52.7, 49.8, 45.2, 42.3 kJ/mol), respec- tively. For comparison energies of three individual hydrogen bonds in the guanine-cytosine base pair were calculated by natural bond orbital (NBO) B3P86/6-311++G** level to all be in the 4.0 to 8.0 kcal/mol (17 to 33 kJ/mol) range [24] .
There is a recent and excellent review (432 references) on the general topic of supramolecular structures and interactions at the vacuum?solid interface [25] . A summary of the forces and interactions that may be present and how they manifest themselves in self-assembly is given. Their discussion includes the role of vdW forces and π-π interactions between molecules and surfaces which is relevant for our work presented here. They provide an overview of the strengths of the wide variety of other molecule-surface interactions and molecule-molecule interactions that guide the assembly of two-dimensional molecular structures on surfaces. Many self-assembled structural examples are presented [25] . Self-as- sembly can create repeated flat pore structures.
This work illustrates in principle how molecules such as tetracene (I), pyrene (O), 1,2-benzanthracene (r), triphenylene (Y) and chrysene (Z) could be used with two-dimensional bilayer graphene pores for site specific “puzzle-ene” adsorption. Binding energy values in these force field calculations should be considered only as representative of the effect that would be observed and not exact. Two-dimensional molecular recognition may play a role in molecule storage, sensors, separations, nanofabrication, or information storage.
Acknowledgements
Support was provided by the Grote Chemistry Fund at the University of Tennessee at Chattanooga (UTC) and the UTC Wheeler Research Fund.
Cite this paper
Rybolt, T.R. and Black, C.B. (2017) Polycyclic Aromatic Hydrocarbon Molecule-Surface Binding Energies in Site Specific Graphene Bilayer Nanopores: A Puzzle-ene Force Field Calculation. Graphene, 6, 72-84. https://doi.org/10.4236/graphene.2017.63006
References
- 1. Choi, W. and Lee, J., Eds. (2012) Graphene: Synthesis and Applications. CRC Press, Boca Raton, Florida.
- 2. Choi, W., Lahiri, I., Seelaboyina, R. and Kang, Y.S. (2010) Synthesis of Graphene and Its Applications: A Review. Critical Reviews in Solid State Materials Sciences, 35, 52-71.
https://doi.org/10.1080/10408430903505036 - 3. Gautam, M. and Jayatissa, A.H. (2012) Adsorption Kinetics of Ammonia Sensing by Graphene Films Decorated with Platinum Nanoparticles. Journal of Applied Physics, 111, 094317/1-094317/9.
https://doi.org/10.1063/1.4714552 - 4. Ren, Y., Zhu, C., Cai, W., Li, H., Ji, H., Kholmanov, I., Wu, Y., Piner, R.D. and Ruoff, R.S. (2012) Detection of Sulfur Dioxide Gas with Graphene Field Effect Transistor. Applied Physics Letters, 100, 163114/1-163114/4.
https://doi.org/10.1063/1.4704803 - 5. Chung, M.G., Kim, D.H., Lee, H.M., Kim, T., Choi, J.H., Seo, D.K., Yoo, J., Hong, S., Kang, T.J. and Kim, Y.H. (2012) Highly Sensitive NO2 Gas Sensor Based on Ozone Treated Graphene. Sensors and Actuators B: Chemical, 166-167, 172-176.
https://doi.org/10.1016/j.snb.2012.02.036 - 6. Zhang, H., Kulkarni, A., Kim, H., Woo, D., Kim, Y., Hong, B. H., Choi, J. and Kim, T. (2011) Detection of Acetone Vapor Using Graphene on Polymer Optical Fiber. Journal of Nanoscience and Nanotechnology, 11, 5939-5943.
https://doi.org/10.1166/jnn.2011.4408 - 7. Yoon, H.J., Jun, D.H., Yang, J.H., Zhou, Z., Yang, S.S. and Chen, M.M. (2011) Carbon Dioxide Gas Sensor Using a Graphene Sheet. Sensors and Actuators B: Chemical, 157, 310-313.
https://doi.org/10.1016/j.snb.2011.03.035 - 8. Zou, Y., Li, F., Zhu, Z.H., Zhao, M.W., Xu, X.G. and Su, X.Y. (2011) An Ab Initio Study on Gas Sensing Properties of Graphene and Si-doped Graphene. European Physical Journal B, 81, 475-479.
https://doi.org/10.1140/epjb/e2011-20225-8 - 9. Leenaerts, O., Partoens, B. and Peeters, F.M. (2008) Adsorption of H2O, NH3, CO, NO2, and NO on Graphene: A First-Principles Study. Physical Review B, 77, 125416/1-125416/6.
https://doi.org/10.1103/PhysRevB.77.125416 - 10. Son, J.H. and Rybolt, T.R. (2013) Force Field Based MM2 Molecule-Surface Binding Energies for Graphite and Graphene. Graphene, 2, 18-34.
https://doi.org/10.4236/graphene.2013.21004 - 11. Rybolt, T.R., Wells, C.E., Sisson, C.R., Black C.B. and Ziegler, K.A. (2007) Evaluation of Molecular Mechanics Calculated Binding Energies for Isolated and Monolayer Organic Molecules on Graphite. Journal of Colloid and Interface Science, 314, 434-445.
https://doi.org/10.1016/j.jcis.2007.05.083 - 12. Rybolt, T.R., Wells, C.E., Thomas, H.E., Goodwin, C.M., Blakely, J.L. and Turner, J.D. (2008) Binding Energies for Alkane Molecules on a Carbon Surface from Gas-Solid Chromatography and Molecular Mechanics. Journal of Colloid and Interface Science, 325, 282-286.
https://doi.org/10.1016/j.jcis.2008.06.043 - 13. Rybolt, T.R., Bivona, K.T., Thomas, H.E. and O’Dell, C.M. (2009) Comparison of Gas-Solid Chromatography and MM2 Force Field Molecular Binding Energies for Greenhouse Gases on a Carbonaceous Surface. Journal of Colloid and Interface Science, 338, 287-292.
https://doi.org/10.1016/j.jcis.2009.06.001 - 14. Jensen, F. (1999) Introduction to Computational Chemistry. John Wiley & Sons, Chichester, England.
- 15. Rybolt, T.R., Trentle, M.C., Rice, M.J. and Thomas, H.E. (2015) Graphene Layer Pore Models for Molecule-Surface Binding Energies. In: Watkins, P., Ed., Molecular Mechanics and Modeling, Nova Publishers, New York, 73-107.
- 16. Wang, J., Chen, Z. and Chen, B. (2014) Adsorption of Polycyclic Aromatic Hydrocarbons by Graphene and Graphene Oxide Nanosheets. Environmental Science and Technology, 48, 4817-4825.
https://doi.org/10.1021/es405227u - 17. Dappe, Y.J., Anderson, M., Balog, R., Hornekaer, L. and Bouju, X. (2015) Adsorption and STM Imaging of Polycyclic Aromatichydrocarbons on Graphene. Physical Review B, 91, 045427/1-045427/8.
https://doi.org/10.1103/PhysRevB.91.045427 - 18. Néel, N. and Kröger, J. (2017) Template Effect of the Graphene Moiré Lattice on Phthalocyanine Assembly. Molecule, 22, 050731-050739.
- 19. Rybolt, T.R. and Wells, C.E. (2009) Molecule-Surface Binding Energies from Molecular Mechanics: Nucleobases on Graphene. In: Chan, H.E., Ed., Graphene and Graphite Materials, Nova Science Publishers, New York, 95-112.
- 20. Kalashnikova, E.V., Kiselev, A.V., Petrova, R.S., Shcherbakova, K.D. and Poshkus, D.P. (1979) Chromatographic Measurements and Molecular Statistical Calculations of Thermodynamic Characteristics of Adsorption of Aromatic and Polycyclic Hydrocarbons on Graphitized Thermal Carbon Black. Chromatographia, 12, 799-802.
https://doi.org/10.1007/BF02260661 - 21. Björk, J., Hanke, F., Palma, C., Samori, P., Cecchini, M. and Persson, M. (2010) Adsorption of Aromatic and Anti-Aromatic Systems on Graphene through π-π Stacking. Journal of Physical Chemistry Letters, 1, 3407-3412.
https://doi.org/10.1021/jz101360k - 22. Zacharia, R., Ulbricht, H. and T. Hertel, T. (2004) Interlayer Cohesive Energy of Graphite from Thermal Desorption of Polyaromatic Hydrocarbons. Physical Review B, 69, Article ID: 155406.
https://doi.org/10.1103/PhysRevB.69.155406 - 23. Tauer, T. P. and Sherrill, C. D. (2005) Beyond the Benzene Dimer: An Investigation of the Additivity of π-π Interactions. Journal of Physical Chemistry A, 109, 10475-10478.
https://doi.org/10.1021/jp0553479 - 24. Szatylowicz, H. and Sadlej-Sosnowska, N. (2010) Characterizing the Strength of Individual Hydrogen Bonds in DNA Base Pairs. Journal of Chemical Information and Modeling, 50, 2151-2161.
https://doi.org/10.1021/ci100288h - 25. Bouju, X., Mattioli, C., Franc, G., Pujol, A. and Gourdon, A. (2017) Bicomponent Supramolecular Architectures at the Vacuum-Solid Interface. Chemical Reviews, 117, 1407-1444.
https://doi.org/10.1021/acs.chemrev.6b00389






