Social Networking
Vol.2 No.3(2013), Article ID:34013,9 pages DOI:10.4236/sn.2013.23012
Finding Statistically Significant Communities in Networks with Weighted Label Propagation
Department of Computer Science, Houghton College, New York, USA
Email: wei.hu@houghton.edu
Copyright © 2013 Wei Hu. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 12, 2013; revised June 18, 2013; accepted July 5, 2013
Keywords: Community Detection; Social Networks; Weighted Label Propagation; Statistical Significance; Zachary’s Karate Club Network
ABSTRACT
Various networks exist in the world today including biological, social, information, and communication networks with the Internet as the largest network of all. One salient structural feature of these networks is the formation of groups or communities of vertices that tend to be more connected to each other within the same group than to those outside. Therefore, the detection of these communities is a topic of great interest and importance in many applications and different algorithms including label propagation have been developed for such purpose. Speaker-listener label propagation algorithm (SLPA) enjoys almost linear time complexity, so desirable in dealing with large networks. As an extension of SLPA, this study presented a novel weighted label propagation algorithm (WLPA), which was tested on four real world social networks with known community structures including the famous Zachary's karate club network. Wilcoxon tests on the communities found in the karate club network by WLPA demonstrated an improved statistical significance over SLPA. With the help of Wilcoxon tests again, we were able to determine the best possible formation of two communities in this network relative to the ground truth partition, which could be used as a new benchmark for assessing community detection algorithms. Finally WLPA predicted better communities than SLPA in two of the three additional real social networks, when compared to the ground truth.
1. Introduction
Any collection of interacting entities could be described as a network, in which each entity is a vertex or node and any pair of interacting vertices is connected with an edge. Thus, networks are a general abstraction of any interactions of different natures including biological, biochemical, communication, computer, and social networks. A network can be also considered as a graph in mathematics, thereby opening a door for introducing many mature techniques into study of networks. However, in a random graph, the distribution of edges among the vertices is highly homogeneous. Real world networks, on the other hand, are often not random at all. For example, there is an observed tendency for vertices to be gathered into groups or clusters. Frequently the vertices within a group are related in some way, and a vertex presents in more than one group may be an indicator of its special role in this network.
Many of the real word networks are known to have the small world property, power law degree distributions, and community structures. A community is a group of vertices that are relatively densely connected to each other within the same group but sparsely to those outside. Social networks describe individuals and their interactions such as friendships and family relationships, and may contain groups based on families or similar interests. On the other side, in a protein-protein interaction network, proteins inside a community may share the same biological or structural function. Community structures, as a significant property of real world networks, play a key role for the functionality of the whole network. Therefore, detection and characterization of communities is of significant practical importance in many applications and has attracted much attention recently due to the increasing popularity of different social networks.
2. Proposed Study and Related Work
The research on community structure has a long history. In 1927 clusters of people in small political bodies were identified, based on the similarity of their voting patterns [1], and in 1955 a search for work groups within a government agency was carried out [2]. With the information of network structure alone, automatic discovery of communities in a network, especially in a large network, can aid greatly to our learning of the complex system represented by the corresponding network. However, this is a nontrivial task, since the number and the sizes of communities in a real world network are typically unknown. In seeking to uncover the community structures in networks, to date many algorithms for community detection, including label propagation algorithm (LPA), have been proposed using various techniques such as graph partitioning, random walks, clustering, optimization, and statistical physics [3]. There are mainly two strategies for finding communities in a network. The first approach identifies one community at a time and allows a vertex belonging to multiple communities, and the second considers a partition of the whole network into disjoint communities when global information about the network is available [4].
With near linear time complexity, LPA [5] and its variants like those in [6,7] are simple and fast, a property very desirable for detecting communities in large networks. These algorithms all belong to the family of agent based community detection algorithms, and can also be viewed as a simple opinion spreading model but with many competing opinions [8]. The idea of propagating labels through a network originated from the L-shell method proposed in [9]. The intuition of LPA is that a single label can quickly become dominant in a densely connected group of vertices whereas it has trouble crossing a sparsely connected region, or in a sense it is trapped inside a densely connected group of vertices. Another advantage of LPA is that this class of algorithms could easily be implemented in parallel or distributed manner.
The original LPA does not require any parameters such as the number or sizes of the communities to be found. At the start of the algorithm, vertices are initially given unique labels typically as integers, meaning each vertex being in its own community. At each iteration every vertex takes the label shared by the majority of its neighbors, thus allowing labels propagate across the entire network. When a tie occurs, one of the majority labels is chosen at random. At the end, vertices with the same label are considered to be in a community. LPA allows the label of a vertex to be updated in two ways: synchronous and asynchronous. In the first method, the new label of each vertex in the current iteration is based on the labels of its neighbors in the previous iteration. In the second method, each label is allowed to use the most current labels of its neighbors whenever available, meaning some labels from the current iteration. Common variants of LPA are usually created with different strategies on the initial label assignment, tie break, and label update rules.
It was discovered that the original LPA tended to form one giant community along with much smaller ones. Leung et al. modified the algorithm by introducing a score for the labels that decreases when the label propagates away from its original vertex. Therefore a single label cannot travel too far and no giant communities can be formed [6]. SLPA is a speaker-listener based label propagation algorithm [7]. Unlike the original LPA, in which a vertex only keeps its most recent label and forgets the labels it received in the previous iterations, the vertex in SLPA stores an array of all the labels it has received. The probability of observing a label in the array is interpreted as the community membership strength. With the knowledge of all the labels, SLPA outperforms the previous versions of LPAs. At the same time, it can also treat weighted and directed networks.
The aim of this study was to propose a novel weighted label propagation algorithm (WLPA), as an extension of SLPA, by introducing a similarity between any two vertices in a network based on the labels each vertex has received during label propagation and using this similarity as a weight of the edge between the two vertices in the next iteration of label propagation. Another feature of our approach was that adding a weight to an edge of two vertices could be repeated in multiple label propagations, making it possible to improve the results in each repetition.
To evaluate the performance of WLPA on community detection, it was tested on four standard real social networks including the well known Zachary’s karate club network. The statistical significance of the communities found in Zachary’s karate club network was measured with Wilcoxon tests. Additionally, we sought to understand the best possible formation of two communities within this social network, which could then be used as a new benchmark for community detection algorithms. Finally the communities found by WLPA in the three remaining networks were examined with several commonly used metrics.
3. Materials and Methods
3.1. Four Real Social Networks
Four real social networks with known community partition were employed to assess the effectiveness of WLPA. The first was the famous Zachary’s karate club network (34 vertices and 78 edges) [10]. Additionally, there were two college football networks and one network of books for US politics. The first college football network was American football games between Division IA colleges during regular season Fall 2000 (115 vertices and 615 edges) [11], and the second was 2006 NCAA Football Bowl Subdivision football schedule (180 vertices and 180 edges) [12]. Vertices in the network represent teams and edges represent the games between the two teams. The network of books is about US politics published around the time of the 2004 presidential election and sold by the online bookseller Amazon.com. Edges between books represent frequent copurchasing of books by the same buyers. The network (105 vertices and 441 edges) was compiled by V. Krebs [13] and augmented by Mark Newman [14] (see also [12]).
3.2. Zachary’s Karate Club Network
The Zachary’s karate club network is a social network of friendships among 34 members of a karate club at a US university in the 1970s. The karate club was observed for a period of three years, from 1970 to 1972 by sociologist Wayne Zachary. Zachary constructed the network of friendships with a variety of measures. Here we used a simple version of his network, with 34 vertices, and 78 edges. Each edge between two vertices was formed when a pair of members consistently interacted in the contexts outside those of karate classes, workouts, and club meetings [10].
Unfortunately, during the observation period, the club was split into two separate smaller clubs over an internal disagreement between club administrator (vertex 1) and principal karate teacher (vertex 33). These two smaller clubs are commonly used as a benchmarker to assess the performance of community detection algorithms [4,15- 17]. We show a visualization of the two smaller clubs, centered on vertex 1 and vertex 33 respectively, in Figure 1 as the ground truth for community structures in this network.
3.3. Community Detection Algorithms: WLPA and SLPA
The original LPA only records one label for each vertex in a network at any time, while SLPA stores an array of all the labels each vertex has received. With this extra piece of information, SLPA is able to perform better than the original LPA. Below we present the SLPA from [8] and our WLPA.
 (a)
(a)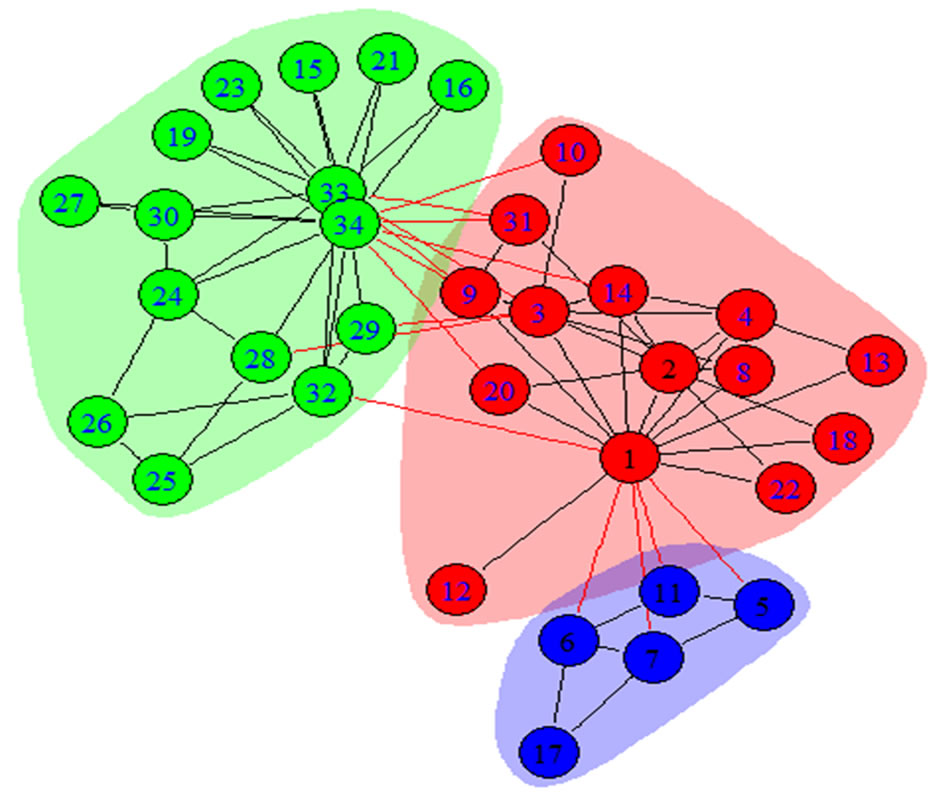 (b)
(b)
Figure 1. Communities of the ground truth and found by SLPA in Zachary’s karate club network. (a) Ground Truth; (b) SLPA.
The novelty of our approach was to introduce a similarity of any two vertices in a network, as an extra piece of information to label propagation, using the labels each vertex has received. With this similarity as a weight of the edge between the two vertices, we were hoping to improve the performance of SLPA to some extent. The rationale of our thoughts was simple: SLPA could outperform the original LPA with extra information that is the array of labels. Could we introduce other extra information into the label propagation process to improve SLPA? It was this question that motivated the coming of our new method WLPA to enrich the label propagation procedure. Another advantage of WLPA was that adding a weight to an edge of two vertices could be repeated in multiple label propagations, making it possible to refine the communities found in each repetition.
4. Results
Our aim was to compare our WLPA with SLPA on four standard real world networks, whose communities are known a priori. We first evaluated WLPA on the famous Zachary's karate club network in depth using statistical analysis. A simple survey of the literature on community detection revealed that very few papers [18-20] explicitly discuss the issue of statistical significance of the communities found by the community detection algorithms. Therefore, the call for statistical analysis in our study was justified and needed. The null hypothesis of our Wilcoxon tests was that there is no difference between the number of internal and external edges incident to a vertex of the community. Then we sought to learn the best possible formation of two communities in this network relative to the ground truth, due to the popularity of the Zachary's karate club network. This kind of investigation could also help to understand whether the ground truth partition is the best given two as the number of communities. To this end, our strategy was to use Wilcoxon tests to assess all possible configurations of two communities in this network using p value as our guide and measure.
Our second task was to evaluate WLPA on the three remaining real world social networks, two of which were college football networks and one was a network of political books. Several commonly used metrics were utilized to gauge the quality of the communities found by WLPA and SLPA.
4.1. Comparison of Our WLPA with SLPA on Zachary’s Karate Club Network
The communities in Zachary's karate club network identified by WLPA and SLPA are displayed in Figures 1 and 2, along with their p values calculated with Wilcoxon tests in Table 1. For the sake of comparison, we also show the two ground truth communities from the original dataset in Figure 1, where vertex 1 (club administrator) and vertex 33 (principal karate teacher) are
 (a)
(a)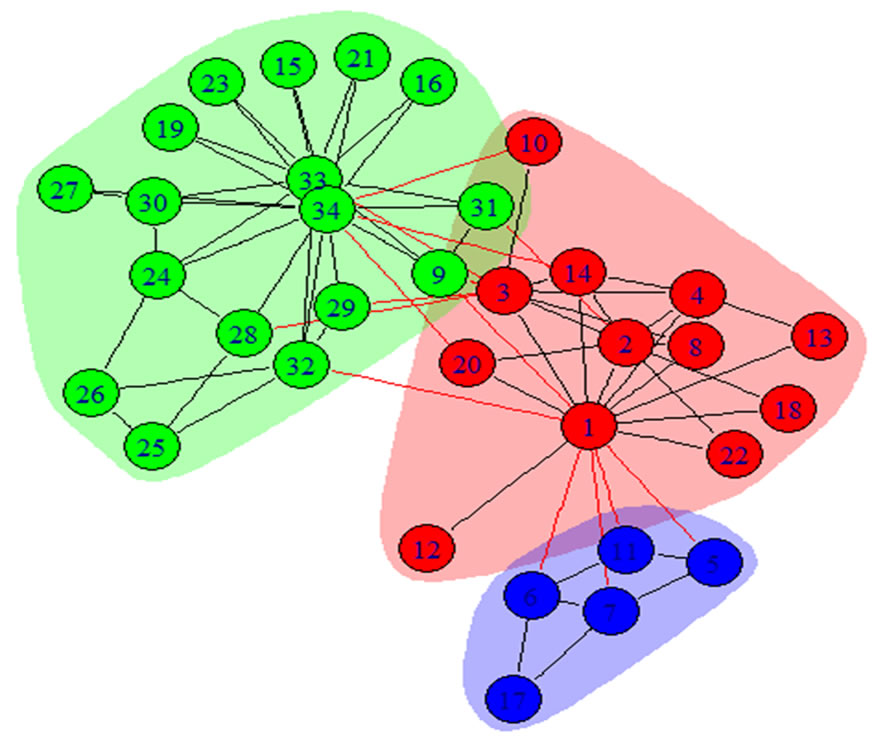 (b)
(b)
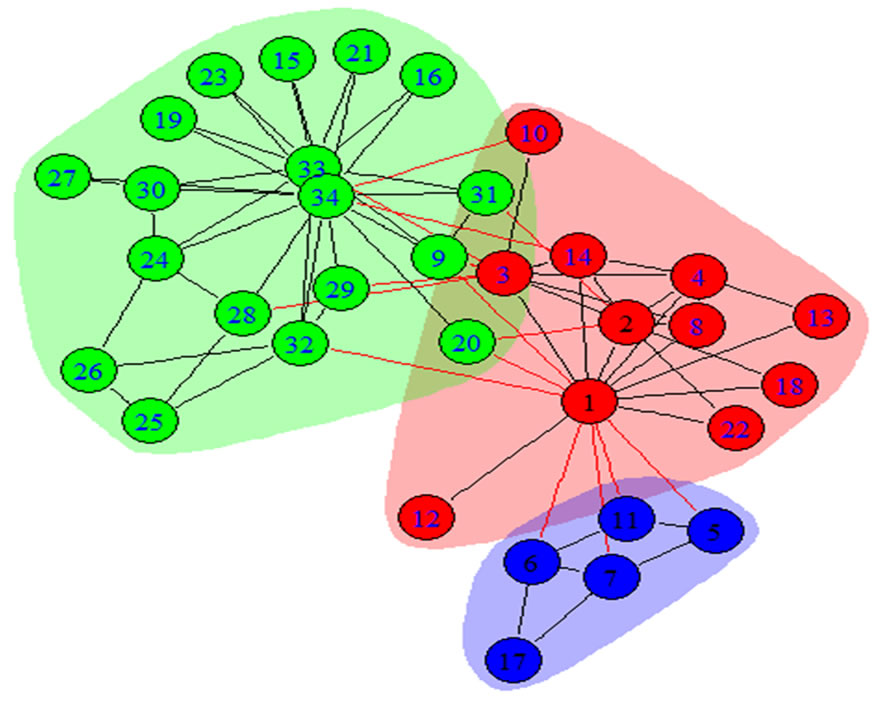
Figure 2. Communities in Zachary’s karate club network found by our WLPA with one and two repetitions. (a) WLPA with one repetition, (b) WLPA with two repetitions.
clearly the center of their communities. Our WLPA was evaluated with one, two, and three repetitions. It seemed that the two repetitions improved the result of one repetition whereas the results of two repetitions and three repetitions were the same, as seen from the reduction of their p values. For this reason only the results up to two repetitions are reported in Figure 2, which demonstrated that the procedure of adding a weight to an edge of two vertices could be repeated in multiple label propagations with the propensity of each repetition improving the previous run. It was easy to see that the findings of our WLPA were better than those of SLPA as reflected by their p values. To ease the notation used in our discussion of the results, we let G1, G2, and G3 denote the three sets of vertices inside the three communities discovered by WLPA with two repetitions: G1 = {9, 24, 26, 25, 28, 29, 30, 27, 31, 32, 33, 15, 16, 19, 21, 23, 34}, G2 = {1, 2, 3, 4, 8, 10, 12, 13, 14, 18, 20, 22}, and G3 = {5, 6, 7, 11, 17}.
Compared to the ground truth communities in Zachary’s karate club network, WLPA misclassified one vertex, 10, with two repetitions, and two vertices, 10 and 20, with one repetition, whereas SLPA misclassified three vertices: 9, 10, and 31. The p values of these communities were consistent with their errors, implying the validity of using p value as an assessment for the quality of the communities found.
4.2. Analysis of the Two Ground Truth Communities in Zachary’s Karate Club Network
In this section, we tried to finish two subtasks. The first was to find the best possible configuration of two communities, compared to the ground truth in this famous network, in terms of their p values of Wilcoxon tests. The second was to investigate the impact of several critical vertices on the boundary of the two ground truth communities.
Using Wilcoxon tests, we were able to evaluate different configurations of two communities in this network (Table 2).The mean of the p values of the two communities was used to measure the quality of the community formation. Our goal was to discover any two communities of a lower average of p values than that of the ground truth configuration. It turned out that there was only one such configuration, the two communities (G1, G2+G3) found by WLPA with two repetitions (Figure 2). It was interesting to notice that not only the average of the two p values, but also each individual p value of (G1, G2+G3) was better than that of the ground truth. Furthermore, our experiments revealed many times that the p value of one community was improved at the expenses of the other. As a result, we could only find one configuration of two communities that had a lower average of p values than that of the ground truth.
A study of Zachary’s karate club network [21] defined the probability of a vertex being in one of the ground truth communities in this network. With help of this probability several key boundary vertices that had a strong impact on the formation of two communities were identified, including vertices 9, 10, 20, 29, and 31 (Figure 1). Here we attempted to find out how these boundary vertices could alter the p values of the two communities if they switched their membership. Vertex 10 had a very low probability in [21], but our direct assessment of the significance suggested this vertex could belong to either one of the two communities without big change of their p values. However, the membership of vertices 9 and 31 was essential due to the large changes of p values caused by their switch. Evidently vertices 20 and 29 were not as a strong impact as vertices 9 and 31 (Table 3).

Table 1. Communities in Zachary’s karate club network found by WLPA with one and two repetitions and SLPA, along with their p values of Wilcoxon tests.
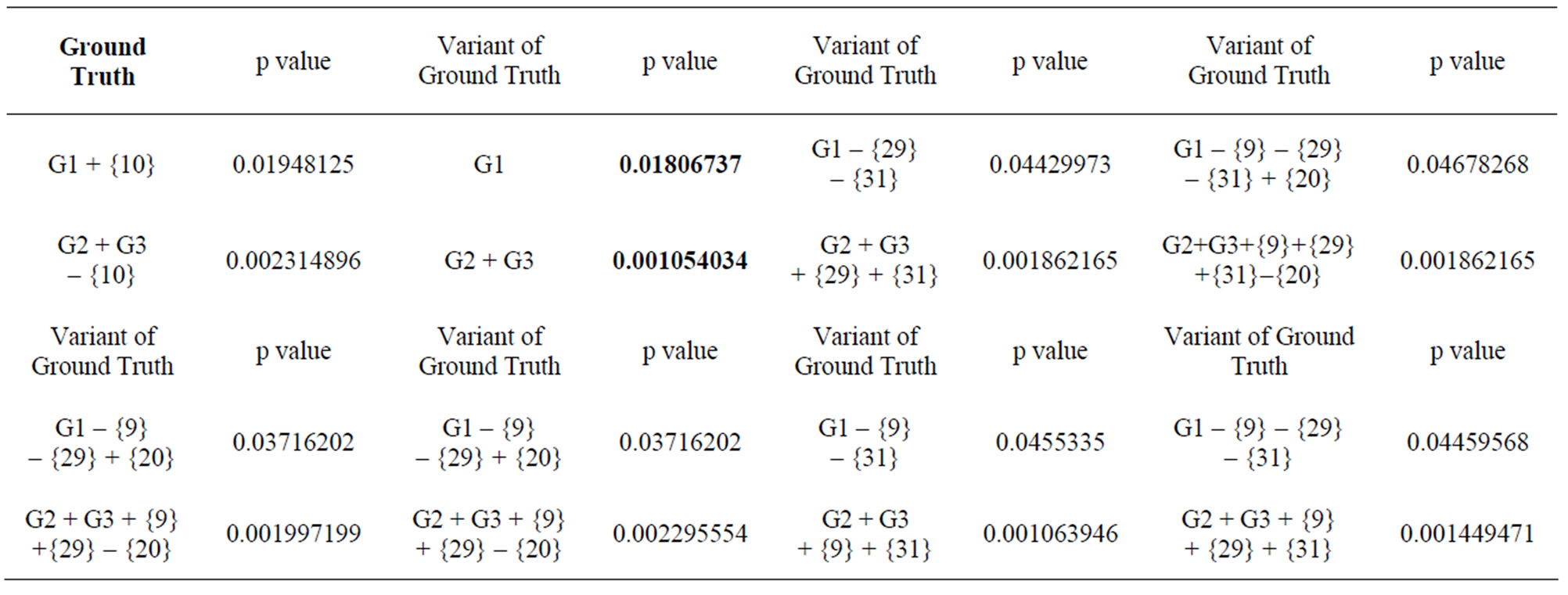
Table 2. P values of the ground truth communities in Zachary's karate club network and their variants.
4.3. Comparison of Our WLPA with SLPA on Three Other Social Networks
Here three additional real social networks were used to assess the effectiveness of WLPA. Two of them were college football networks and one was a network of political books (Figures 3-5). Several common metrics were selected to measure the similarity of the communities between the ground truth and those found by of WLPA or SLPA. These metrics were Variation of Information (VI) [22], Normalized Mutual Information (NMI) [23], Split Join Distance (SJD) [24], and Rand Index (RI) [25]. If two collections of communities in a network are the same then their NMI = RI= 1 and VI = SJD = 0. The range of NMI and RI is from 0 to 1, the range of VI is nonnegative real numbers, and the range of SJD is natural numbers. Therefore if the predicted communities in a network are close to those of its ground truth, their values of NMI and RI should be close to 1 and the values of VI
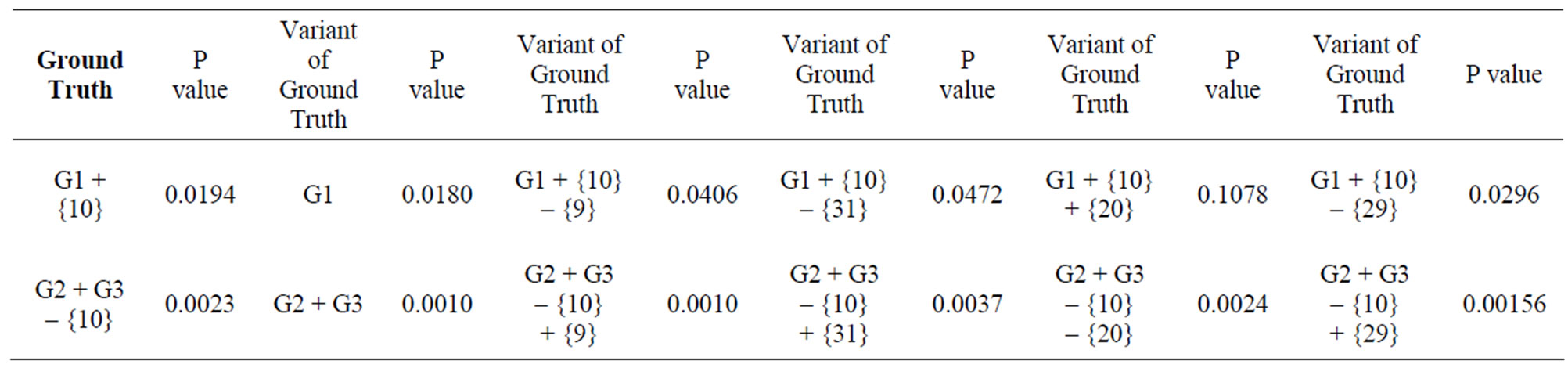
Table 3. Change of p values when key boundary vertices switched their community membership in Zachary's karate club network.

Figure 3. College football network in 2000 with the ground truth communities in different colors [11].
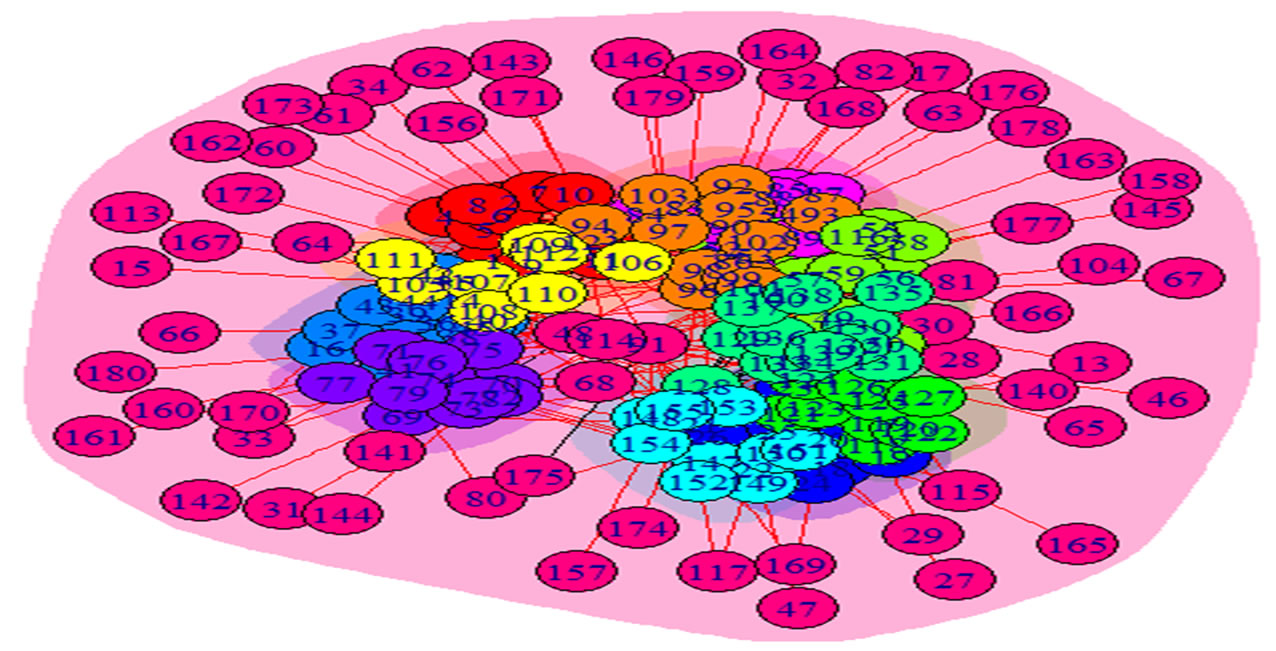
Figure 4. College football network in 2006 with the ground truth communities in different colors [12].
and SJD close to 0. The number of communities of the ground truth and those predicted by WLPA and SLPA predicted better communities than SLPA in the two football networks, but not in the network of political books, when compared to the ground truth communities. Looking at the number of communities found in the two football networks, WLPA made a substantial improvement over SLPA. Further, WLPA was able to predict the same number of communities in the network of political books as SLPA is reported in Table 4 and the comparesons of communities found by WLPA and SLPA with those of the ground truth are in Table 5. It was obvious that WLPA predicted better communities than SLPA in the two football networks, but not in the network of political books, when compared to the ground truth communities. Looking at the number of communities found in the two football networks, WLPA made a substantial improvement over SLPA. Further, WLPA was able to predict the same number of communities in the network of political books as SLPA.
5. Conclusions
Many complex systems in nature and science can be best represented as networks. Community structures contained in real world networks play an important role in determining the functionality of the whole network. With the advent of several popular social networks, there is a surge of interest in understanding the key properties of these networks, especially in the last few years.
This study proposed a weighted label propagation algorithm (WLPA) based on similarity for community detection, as an extension of SPLA. Our algorithm worked by introducing a similarity between any two vertices in a net work based on the labels each vertex has received during label propagation, and then using this similarity as a weight of the edge between the two vertices in the next iteration of label propagation. One surprising feature of
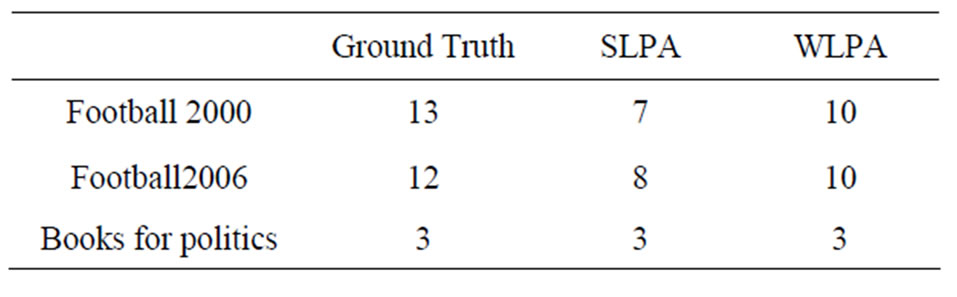
Table 4. Number of communities of the ground truth and those predicted by WLPA and SLPA in the three remaining real social networks.
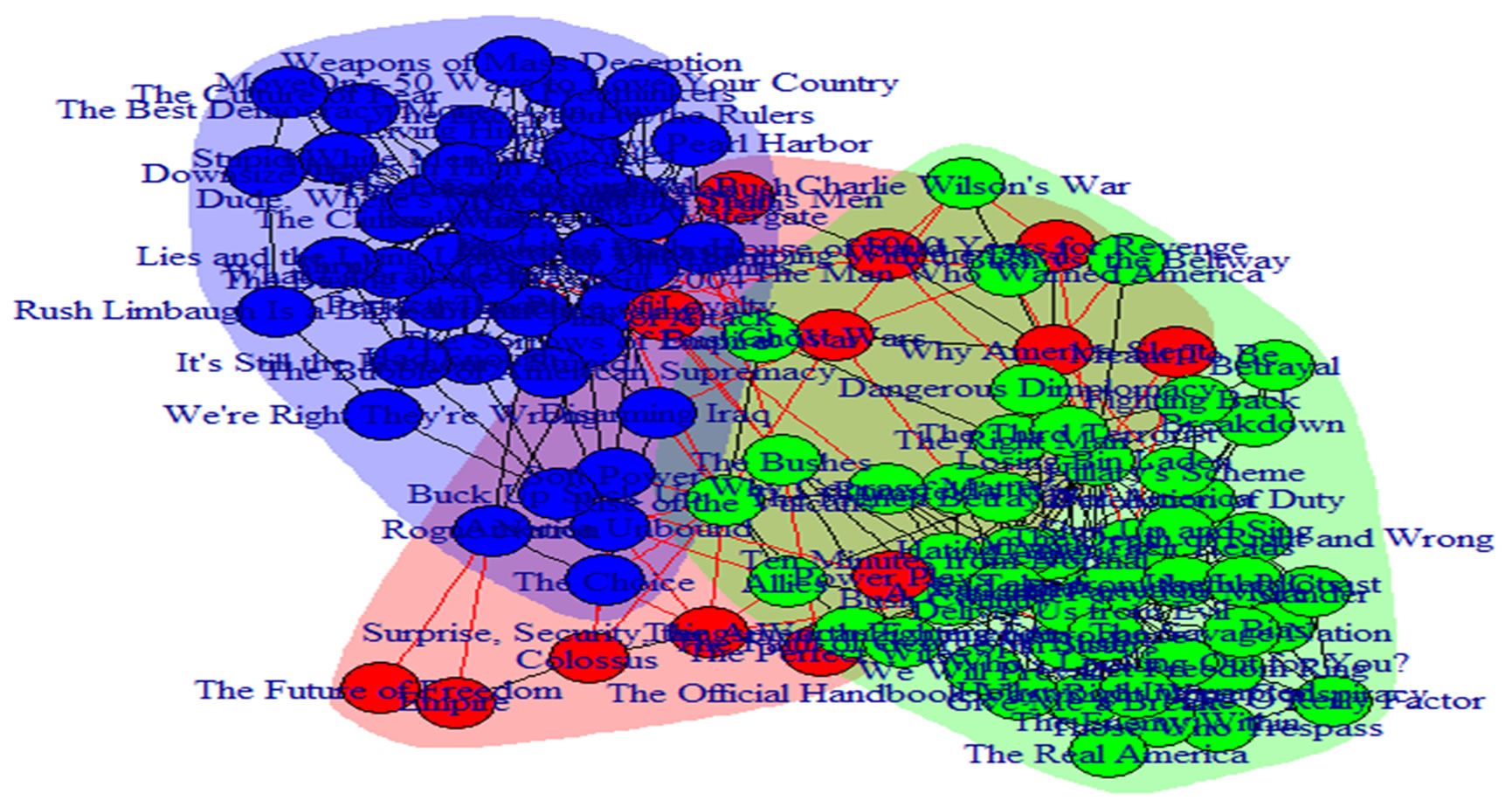
Figure 5. Network of political books with the ground truth communities in different colors [13,14].

Table 5. Comparison of the communities found by WLPA and SLPAwith those of the ground truth in the three remaining real social networks using different metrics.
our method was that adding a weight to an edge of two vertices could be repeated multiple times, with the potential to improve performance of the algorithm in each run.
Our WLPA was evaluated on four standard real world social networks with known community information, including the famous Zachary’s karate club. Wilcoxon tests on the communalities found in the karate club by WLPA indicated an improvement of their statistical significance over SLPA. With the same statistical approach, we were able to determine the best possible formation of two communities in this network, compared to the ground truth configuration, which could be used as a new benchmark for community detection algorithms. Furthermore, the test of WLPA on the three remaining real social networks produced better communities in two of the three networks than SLPA when compared to the ground truth.
6. Acknowledgements
We thank Houghton College for its financial support.
REFERENCES
- S. A. Rice, “The Identification of Blocs in Small Political Bodies,” The American Political Science Review, Vol. 21, No. 3, 1927, pp. 619-627. doi:10.2307/1945514
- R. S. Weiss and E. Jacobson, “A Method for the Analysis of the Structure of Complex Organizations,” American Sociological Review, Vol. 20, No. 6, 1955, pp. 661-668. doi:10.2307/2088670
- S. Fortunato, “Community Detection in Graphs,” Physics Reports, Vol. 486, No. 3-5, 2010, pp. 75-174. doi:10.1016/j.physrep.2009.11.002
- G. Agarwal and D. Kempe, “Modularity-Maximizing Network Communities Using Mathematical Programming,” The European Physical Journal B, Vol. 66, No. 3, 2008, pp. 409-418. doi:10.1140/epjb/e2008-00425-1
- U. N. Raghavan, R. Albert and S. Kumara, “Near Linear Time Algorithm to Detect Community Structures in LargeScale Networks,” Physical Review E, Vol. 76, 2007, Article ID: 036106. doi:10.1103/PhysRevE.76.036106
- I. X. Y. Leung, P. Hui, P. Lio and J. Crowcroft, “Towards Real-Time Community Detection in Large Networks,” Physical Review E, Vol. 79, 2009, Article ID: 066107. doi:10.1103/PhysRevE.79.066107
- J. Xie, B. K. Szymanski and X. Liu, “SLPA: Uncovering Overlapping Communities in Social Networks via A Speaker-Listener Interaction Dynamic Process,” IEEE ICDM Workshop on DMCCI 2011, Vancouver, 2011, pp 344-349.
- J. R. Xie, “Agent-Based Dynamics Modeling for Opinion Spreading and Community Detection in Large-Scale Social Networks,” Rensselaer Polytechnic Institute, Troy, 2012.
- J. Bagrow and E. Bollt, “A Local Method for Detecting Communities,” Physical Review E, Vol. 72, 2005, Article ID: 046108. doi:10.1103/PhysRevE.72.046108
- W. W. Zachary, “An Information Flow Model for Conflict and Fission in Small Groups,” Journal of Anthropological Research, Vol. 33, 1977, pp. 452-473.
- M. Girvan and M. E. J. Newman, “Community Structure in Social and Biological Networks,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 99, 2002, pp. 7821-7826. doi:10.1073/pnas.122653799
- X. Xu, N. Yuruk, Z. Feng and T. A. J. Schweiger, “Scan: A Structural Clustering Algorithm for Networks,” Proceedings of 2007 International Conference Knowledge Discovery and Data Mining, San Jose, August 2007, pp. 824-833.
- http://www.orgnet.com/
- http://www-personal.umich.edu/~mejn/netdata/
- M. Girvan and M. E. J. Newman, “Community Structure in Social and Biological Networks,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 99, No. 12, 2002, pp. 8271-8276. doi:10.1073/pnas.122653799
- M. A. Porter, J.-P. Onnela and P. J. Mucha, “Communities in Networks,” Notices of the American Mathematical Society, Vol. 56, No. 9, 2009, pp. 1082-1097, 1164-1166.
- A. Medus, G. Acuna, and C. Dorso, “Detection of Community Structures in Networks via Global Optimization,” Physica A: Statistical Mechanics and Its Applications, Vol. 358, No. 2-4, 2005, pp. 593-604.
- A. Lancichinetti, F. Radicchi, J. J. Ramasco and S. Fortunato, “Finding Statistically Significant Communities in Networks,” PLoS ONE, Vol. 6, No. 4, 2011, Article ID: e18961. doi:10.1371/journal.pone.0018961
- A. Mirshahvalad, J. Lindholm, M. Derlén and M. Rosvall, “Significant Communities in Large Sparse Networks,” PLoS ONE, Vol. 7, No. 3, 2012, Article ID: e33721. doi:10.1371/journal.pone.0033721
- J. Reichardt and S. Bornholdt, “Statistical Mechanics of Community Detection,” Physical Review E, Vol. 74, 2006, Article ID: 016110. doi:10.1103/PhysRevE.74.016110
- J. P. Ferry, J. O. Bumgarner and S. T. Ahearn, “Probabilistic Community Detection in Networks,” The 14th International Conference on Information Fusion, Chicago, 5-8 July 2011, pp. 1-8.
- M. Meila, “Comparing Clusterings by the Variation of Information,” In: B. Scholkopf and M. K. Warmuth, Eds., Learning Theory and Kernel Machines: 16th Annual Conference on Computational Learning Theory and 7th Kernel Workshop, Springer, Washington DC, 2003, pp. 173-187.
- L. Danon, A. Diaz-Guilera, J. Duch and A. Arenas, “Comparing Community Structure Identification,” Journal of Statistical Mechanics, No. 9, 2005, ArticleID: P09008. doi:10.1088/1742-5468/2005/09/P09008
- S. van Dongen, “Performance Criteria for Graph Clustering and Markov Cluster Experiments,” Technical Report INS-R0012, National Research Institute for Mathematics and Computer Science in the Netherlands, Amsterdam, 2000.
- W. M. Rand, “Objective Criteria for the Evaluation of Clustering Methods,” Journal of the American Statistical Association, Vol. 66, No. 336, 1971, pp. 846-850. doi:10.1080/01621459.1971.10482356

