International Journal of Medical Physics, Clinical Engineering and Radiation Oncology
Vol.04 No.03(2015), Article ID:58191,6 pages
10.4236/ijmpcero.2015.43025
On the Nonequilibrium of Radiation-Induced Bystander Effects in Tumor Surface and Its Implications in Radiation Therapy
R. Vaitheeswaran1,2, K. J. Maria Das3
1Philips Radiation Oncology Systems, Philips India Ltd., Bangalore, India
2Research & Development Center, Bharathiar University, Coimbatore, India
3Department of Radiotherapy, Sanjay Gandhi Post Graduate Institute of Medical Sciences, Lucknow, India
Email: vaithe1985@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 May 2015; accepted 19 July 2015; published 22 July 2015
ABSTRACT
This work aims to theoretically show the development of a nonequilibrium of radiation-induced bystander effect (RIBE) under steep dose gradient regions that typically occur in the field edges of a beam. We applied the kinetics model proposed by (McMahon et al. 2013) for in vivo conditions coupled with a hypothesis called “Layer-limited bystander signaling (LLBS)” to demonstrate 1) an enhancement in TCP (i.e. Enhanced TCP or ETCP) due to bystander signals, 2) the development of nonequilibrium of RIBE under steep dose gradient regions and 3) the reduction in ETCP in the surface of Clinical Target Volume (CTV) due to the non-equilibrium of RIBE. We incorporated the elements of RIBE directly in the existing Poisson LQ model available in Pinnacle3 TPS (Version 9.10.0) to compute the percentage reduction of ETCP in the tumor surface due to nonequilibrium of RIBE. The percentage improvement in TCP obtained in tumor surface by accounting for RIBE is about 46% lower than that obtained in the interior of the tumor. This suggests that relatively more number of cancerous cells might survive in the vicinity of tumor surface. The result obtained from the study is indicative of an additional uncertainty component associated with radiation treatment. Hence, this paper suggests that the radiation treatments employing steep dose gradients could be biophysically different in many ways.
Keywords:
Bystander Effect, TCP, RIBE, CTV, IMRT, Dose Gradients

1. Introduction
Intensity modulated Radiation Therapy (IMRT) allows for a highly conformal dose distribution to be planned for a target volume, while effectively sparing the surrounding healthy tissues or organs. Clinical trials have shown a promising tumor control and lower normal tissue complications. The reported advantages in IMRT arise from the ability to produce steep dose gradients between tumor surface and surrounding normal tissue.
In IMRT, the desired uniform dose distribution to target volume is achieved by producing an inhomogeneous X-ray dose distribution from multiple directions. Many investigators have suggested methods to account for changes in radiation response of tumour cells when exposed to inhomogeneous dose distributions [1] -[3] . These models are based on the hypothesis that the probability of killing tumour cells at a given point is a function solely of the dose delivered to that point [4] . However, recent in vitro studies have proven various non-localiza- tion effects as a consequence of localized absorbed dose, which are collectively called as radiation-induced bystander effects (RIBE) [5] -[10] . Additionally, recent studies have indicated that direct exposure to high doses of radiation does not mitigate signaling effects [9] [10] .
Also the implications of RIBE for modulated X-ray fields have been reported [7] -[9] [11] . Recently McMahon et al. proposed a generalized kinetics model [12] of radiation-induced intercellular signaling which incorporates signal production and response kinetics together with the effects of direct irradiation. This model suggested that RIBE might play a significant role in determining cellular survival, even in directly irradiated populations. Very recently McMahon et al. applied their own model to in vivo conditions and investigated if their predictions based on in vitro conditions can be reconciled with in vivo knowledge [13] . In the same paper they mentioned about the issue of non-equilibrium of RIBE in tumor surfaces and its related consequences.
In this work, we applied the kinetics model proposed by McMahon et al. for in vivo conditions [12] coupled with a hypothesis called “Layer-limited bystander signaling (LLBS)” to quantitatively demonstrate 1) an enhancement in TCP (i.e. Enhanced TCP or ETCP) due to bystander signals, 2) the development of nonequilibrium of RIBE under steep dose gradient regions and 3) the reduction in ETCP in the surface of Clinical Target Volume (CTV) due to the non-equilibrium of RIBE.
2. Materials and Methods
2.1. Enhanced TCP Due to RIBE
McMahon et al. modelled [12] the intercellular communications as a signal concentration, ρ, which is spatially- and temporally-dependent. In this work we adopted the same approach to represent bystander signals. It was shown that, if the signal spreads out via diffusion, then the signal concentration in the system evolves according to
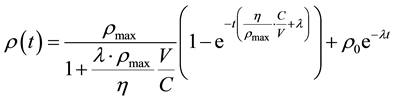 (1)
(1)
where  is the signal concentration at time t;
is the signal concentration at time t;  is the signal concentration at t = 0;
is the signal concentration at t = 0; 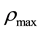 is the cell’s local signal concentration; C is the number of cells; V is the total media volume;
is the cell’s local signal concentration; C is the number of cells; V is the total media volume; 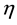 is the rate of signal production by a cell if the local signal concentration is 0;
is the rate of signal production by a cell if the local signal concentration is 0;  is the rate constant for exponential decay of signals.
is the rate constant for exponential decay of signals.
In Equation (1), it is considered that a cell receiving dose D will continue to emit signals for a time of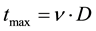 , where
, where  is a constant, characteristic of the cell line. Hence a cell that has received a higher dose will continue to emit signal for a longer time causing a greater probability of damage to the cells in its vicinity as compared to a cell that has received relatively lesser dose.
is a constant, characteristic of the cell line. Hence a cell that has received a higher dose will continue to emit signal for a longer time causing a greater probability of damage to the cells in its vicinity as compared to a cell that has received relatively lesser dose.
Consider two clusters (Cluster A and B) of equal number of tumor cell populations whose center is separated by a distance . Assume that both clusters are simultaneously exposed to a fractional dose of d (to be delivered in n fractions). The tumor control probability (TCP) for the cell populations can be calculated based on the Linear Quadratic tissue response function proposed in [1] .
. Assume that both clusters are simultaneously exposed to a fractional dose of d (to be delivered in n fractions). The tumor control probability (TCP) for the cell populations can be calculated based on the Linear Quadratic tissue response function proposed in [1] .
TCP for the cell populations in Cluster A is given by:
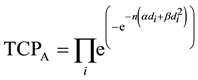 (2)
(2)
where 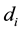 is the dose absorbed by ith cell in Cluster A per fraction.
is the dose absorbed by ith cell in Cluster A per fraction.
TCP for the cell populations in Cluster B is given by:
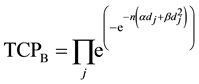 (3)
(3)
where 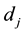 is the dose absorbed by jth cell in Cluster B per fraction.
is the dose absorbed by jth cell in Cluster B per fraction.
In Equations (2) and (3), the parameters α and β represent the linear and quadratic components of the LQ model respectively.
Assuming α/β = 10, and the dose delivered per fraction is 2 Gy, Equations (2) and (3) is reduced to:
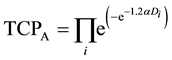 (4)
(4)
 (5)
(5)
where D is the total dose, i.e. D = n ´ d.
If we assume the absorption of signal ρ leads to an overall reduction in surviving fraction, the enhanced tumor control probability (ETCP) for the tumor population in Cluster A can be
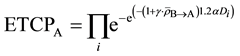 (6)
(6)
where 

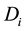
ETCP for the tumor population in Cluster B is given by
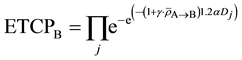

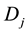
Let us assume that both clusters receive equal amount of dose per fraction at the same time. As mentioned before, the cells receiving dose will continue to emit signals only for a finite amount of time in proportionate to the amount of absorbed dose. Hence, it is apparent that the amount of bystander signal received by both tumor clusters from each other would reach a dynamic equilibrium in time t leading to same overall biological effect, that is,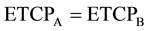
However, the dynamic equilibrium of the signals received by the tumor clusters from each other will be impaired if the Clusters A and B are exposed to entirely different magnitudes of dose at the same time. Such scenarios usually occur in the field edges of a beam, that is, between tumor and normal tissue surfaces, wherein a steep dose gradient is produced.
2.2. Reduction of ETCP in Tumor Surface
In order to prove the reduction of ETCP in tumor surface, we have used a hypothesis called “Layer-limited bystander signaling (LLBS)”. According to LLBS hypothesis, in a 2D geometry, the entire bystander signal received by a given Layer of cells is only from the nearest Layers on both sides, which is illustrated in Figure 1. This hypothesis can be justified because various in vitro experiments have confirmed that RIBE is spatially and temporally limited and has a finite range of impact from its point of origin in a tissue-like medium.
Consider five Layers of cells as shown in Figure 1. Layers P, Q and R comprise equal number of tumor cells with equal cell density receiving the prescribed tumoricidal dose. Layers S and T comprise normal cells receiving very low dose. So the dose gradient is actually formed across Layers R and S, wherein R represents the tumor surface. Here tumor surface implies the surface of clinical target volume (CTV).
Figure 1. Illustration of Layer-limited bystander signaling (LLBS) process. The Layers P, Q and R comprise tumor cells receiving the prescribed tumoricidal dose and Layers S and T comprise normal cells receiving very low dose.
According to LLBS hypothesis, the entire bystander signal that Layer Q would get is only from Layers P and R. Likewise, the entire bystander signal that Layer R would get is only from Layers Q and S. It is important to note that the thickness of the Layers is modeled in such a way that one Layer would completely absorb the signals received from its nearest Layer without any further transmission of the signals to other Layers. It was reported that the propagation of RIBE through radicals was found to reach up to 1 mm from the point of origin [14] . Considering other pathways for signaling process, a Layer thickness of 2 mm was considered to appropriate in the context of LLBS hypothesis.
Now let us compute ETCP at Layers Q and R as shown below:

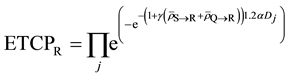
where, 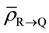
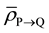
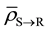
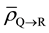
Since Layer S is receiving relatively very low dose, the cells in Layer S will cease to emit signals relatively quickly. Hence the cumulative of signal received by the cells in Layer R from Layer S will be negligible as compared to the amount of signal received from Layer Q over a period of time t, which is much greater than 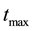

Also one can say that 
Hence,

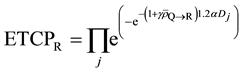
Therefore,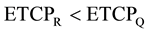
This theoretical argument indicates a relative reduction in the ETCP of the cells at the tumor surface (i.e. CTV surface) in spite of getting exposed to the same amount of physical dose as received by the cells inside the tumor volume.
3. Results
We incorporated the elements of RIBE directly in the existing Poisson LQ model available in Pinnacle3 TPS (Version 9.10.0) to compute ETCP. We created 2 mm thick Layers in a model water phantom mimicking the illustration given in Figure 1 using Pinnacle3 TPS. The volume of each Layer was 1 cc. We assumed α/β = 10 for Layers P, Q and R. We used a fractionation scheme of 2 Gy for 25 fractions, covering at least 95% volume of each Layer. We simulated the exposure of the Layers with a single-field 6-MV photon beam produced with a Varian linear accelerator (Varian Clinac 2100).
The field edge of the beam was set with a margin of 1 mm from the edge of Layer R to the edge of the field (defined only by Jaw). The beam MU was adjusted in such a way that the mean dose obtained in Layers P, Q and R is 50 Gy. Consequently, the Layers P and Q receive a minimum dose of 44 Gy and a maximum dose of 57 Gy in 25 fractions; Layer R receives a minimum dose of 39 Gy, and a maximum dose of 57 Gy in 25 fractions. We used a dose grid setting of 2 mm in X, Y and Z planes and computed the dose using Convolution/Superpo- sition algorithm. In addition, we assumed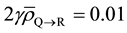
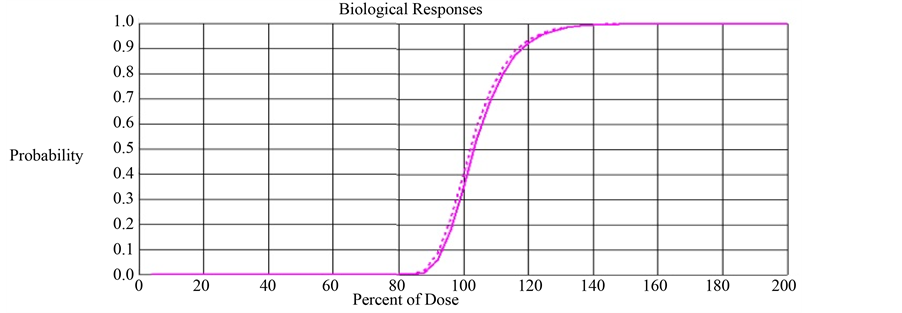
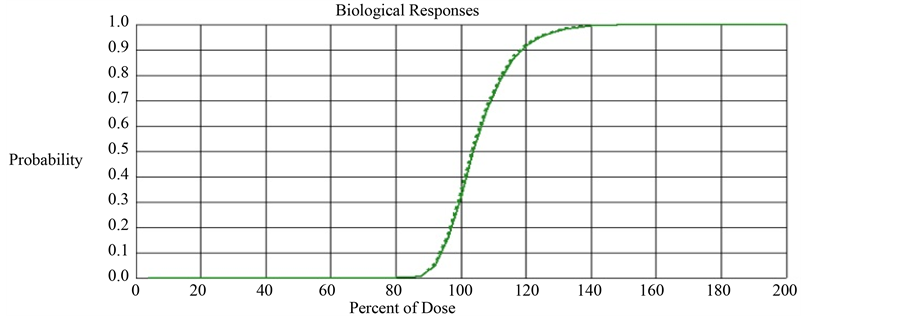
With this parameter setting, we computed TCP and ETCP for Layers Q and R. The TCP and ETCP for Layer Q was 0.355 and 0.405 respectively, meaning 14% improvement in TCP due to the impact of bystander signals. The TCP and ETCP for Layer R was 0.328 and 0.353 respectively, meaning 7.6% improvement in TCP due to the impact of bystander signals. This implies that the percentage improvement in TCP obtained in Layer R is 45.7% lower than that obtained in Layer Q. Figure 2 compares the TCP and ETCP curves for Layers Q and Figure 3 compares the TCP and ETCP curves for Layer R.
Figure 2. Comparison of TCP (solid line) and ETCP (dotted line) curves for Layer Q. The computed TCP and ETCP for Layer Q was 0.355 and 0.405 respectively.
Figure 3. Comparison of TCP (solid line) and ETCP (dotted line) curves for Layer R. The computed TCP and ETCP for Layer R was 0.328 and 0.353 respectively.
4. Discussion
It was not previously unknown that the cells in tumor surface are prone to get underdosed due to internal organ motion and set-up uncertainty related factors. This is why a planning target volume (PTV) is added to CTV. In this paper, it is argued that even if the CTV surface is given an equal amount of dose as given to the interiors of the CTV, there will be a measurable reduction in ETCP at the surface, when a steep dose gradient is formed right next to the CTV edge. The results indicate that the percentage improvement in ETCP induced by RIBE is 45.7% lower in tumor surface than that in the interior of the tumor. This implies that more number of cancerous cells might survive in the vicinity of tumor surface. We agree that this prediction is not validated by any experimental observations in vivo. But the basis for our work is McMahon’s model [12] , which was developed upon a large bank of experimental data. In other words, the predicted non-equilibrium of RIBE in tumor surfaces is a direct implication of McMahon’s kinetics model [12] when in vivo conditions are considered.
Current notion of PTV is to mitigate the risk of geometric miss of CTV due to internal motion and set-up uncertainty. The concept of PTV could mitigate the risk of reduction of ETCP in CTV surface to an extent as long as the intended gap between CTV and PTV is maintained. However, during the course of RT (inter and intra fraction), it is possible that CTV margin closely approaches PTV margin, which could increase the risk of causing a reduction of ETCP in CTV surface. This is indicative of an additional uncertainty component associated with radiation treatments. Moreover, the proposed model shows that the degree of reduction in ETCP is directly proportional to the dose gradient produced in the tumor surface. So a huge reduction in ETCP could be expected for treatments employing more intensity modulation such as IMRT and spot scanned proton therapy. In IMRT, the lateral edges of the field are expected to cause the reduction of ETCP, whereas in the case of proton therapy, the distal edge of the beam is expected to cause the reduction.
The assumption of 1% change in α due to the impact of RIBE is based on the theoretical planning study by McMahon et al. [13] , where they have reported a reduction of 3 Gy in the “signal-adjusted” mean dose for a 74 Gy plan inside the primary radiation field, when the signal range is assumed to be 2 cm, meaning a 4% overall change in dose. This implies about 4% change in α if Equations of type 4 or 5 is used. In our case we assume the signal range to be 1 mm and hence we have assumed a less percentage change in α (i.e. 1%) in our study. However, there is no good guidance available till date for in vivo conditions as to how much should be the value for the increase in alpha for conventional fractionation schemes. In fact, one can repeat the study with different “signal range values” (say 1 mm to 2 cm) and “enhanced alpha” values (say, 1% to 10%) and investigate how ETCP varies at the tumor surface for different tumor types and beam geometry. Besides, it is to be noted that the objective of our work is not to accurately quantify the impact of RIBE on α, but to demonstrate the development of nonequilibrium of RIBE in tumor surfaces due to steep dose gradients, provided RIBE is applicable at high doses and direct exposures.
As far as the extendibility of the proposed model is concerned, inputting a reasonable value for the factor 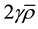
5. Conclusion
In this work, we have theoretically demonstrated the development of a nonequilibrium of RIBE under steep dose gradient regions. The results obtained in the study show that the percentage improvement in TCP obtained in tumor surface is about 46% lower than that obtained in the interior of the tumor. This suggests that relatively more number of cancerous cells might survive in the vicinity of tumor surface. Also this is indicative of an additional uncertainty component associated with radiation treatment. Hence, this paper suggests that the radiation treatments employing steep dose gradients could be biophysically different in many ways.
Cite this paper
R.Vaitheeswaran,K. J.Maria Das,11, (2015) On the Nonequilibrium of Radiation-Induced Bystander Effects in Tumor Surface and Its Implications in Radiation Therapy. International Journal of Medical Physics, Clinical Engineering and Radiation Oncology,04,208-214. doi: 10.4236/ijmpcero.2015.43025
References
- 1. Kallman, P., Agren, A. and Brahme, A. (1992) Tumour and Normal Tissue Responses to Fractionated Non-Uniform Dose Delivery. International Journal of Radiation Biology, 62, 249-262.
http://dx.doi.org/10.1080/09553009214552071 - 2. Ebert, M.A. and Hoban, P.W. (1996) Some Characteristics of Tumour Control Probability for Heterogeneous Tumours. Physics in Medicine and Biology, 41, 2125-2133.
http://dx.doi.org/10.1088/0031-9155/41/10/019 - 3. Niemierko, A. and Goitein, M. (1993) Implementation of a Model for Estimating Tumor Control Probability for an Inhomogeneously Irradiated Tumor. Radiotherapy and Oncology, 29, 140-147.
http://dx.doi.org/10.1016/0167-8140(93)90239-5 - 4. Hall, E.J. and Giaccia, A.J. (2006) Radiobiology for the Radiologist. Lippincott Williams & Wilkins.
- 5. Mothersill, C. and Seymour, C.B. (1998) Cell-Cell Contact during Gamma Irradiation Is Not Required to Induce a Bystander Effect in Normal Human Keratinocytes: Evidence for Release during Irradiation of a Signal Controlling Survival into the Medium. Radiation Research, 149, 256-262.
http://dx.doi.org/10.2307/3579958 - 6. Nagasawa, H. and Little, J.B. (1999) Unexpected Sensitivity to the Induction of Mutations by Very Low Doses of Alpha-Particle Radiation: Evidence for a Bystander Effect. Radiation Research, 152, 552-557.
http://dx.doi.org/10.2307/3580153 - 7. Suchowerska, N., Ebert, M.A., Zhang, M. and Jackson, M. (2005) In Vitro Response of Tumour Cells to Non-Uniform Irradiation. Physics in Medicine and Biology, 50, 3041-3051.
http://dx.doi.org/10.1088/0031-9155/50/13/005 - 8. Butterworth, KT., McGarry, C.K., O’Sullivan, J.M., Hounsell, A.R. and Prise, K.M. (2010) A Study of the Biological Effects of Modulated 6 MV Radiation Fields. Physics in Medicine and Biology, 55, 1607-1618.
http://dx.doi.org/10.1088/0031-9155/55/6/005 - 9. Butterworth, K.T., McGarry, C.K., Trainor, C., O’Sullivan, J.M., Hounsell, A.R., et al. (2011) Out-of-Field Cell Survival Following Exposure to Intensity-Modulated Radiation Fields. International Journal of Radiation Oncology*Biology*Physics, 79, 1516-1522.
http://dx.doi.org/10.1016/j.ijrobp.2010.11.034 - 10. Butterworth, K.T., McGarry, C.K., Trainor, C., McMahon, S.J., O’Sullivan, J.M., et al. (2012) Dose, Dose-Rate and Field Size Effects on Cell Survival Following expoSure to Non-Uniform Radiation Fields. Physics in Medicine and Biology, 57, 3197-3206.
http://dx.doi.org/10.1088/0031-9155/57/10/3197 - 11. Bromley, R., et al. (2009) Predicting the Clonogenic Survival of A549 Cells after Modulated X-Ray Irradiation Using the Linear Quadratic Model. Physics in Medicine and Biology, 54, 187.
http://dx.doi.org/10.1088/0031-9155/54/2/002 - 12. McMahon, S.J., et al. (2013) A Kinetic-Based Model of Radiation-Induced Intercellular Signaling. PloS One, 8.
http://dx.doi.org/10.1371/journal.pone.0054526 - 13. McMahon., S.J., et al. (2013) Implications of Intercellular Signaling for Radiation Therapy: A Theoretical Dose-Planning Study. International Journal of Radiation Oncology*Biology*Physics, 87, 1148-1154.
http://dx.doi.org/10.1016/j.ijrobp.2013.08.021 - 14. Belyakov, O.V., Mitchell, S., Parikh, D., Randers-Pehrson, G., Marino, S., et al. (2005) Biological Effects in Unirradiated Human Tissue Induced by Radiation Damage up to 1 mm Away. Proceedings of the National Academy of Sciences of the United States of America, 102, 14203-14208.
http://dx.doi.org/10.1073/pnas.0505020102