Advances in Computed Tomography
Vol.2 No.4(2013), Article ID:41095,8 pages DOI:10.4236/act.2013.24023
Numerical Studies of the Generalized l1 Greedy Algorithm for Sparse Signals
1Department of Mathematics, Francis Marion University, Florence, USA
2School of Science Technology, American Public University System, Manassas, USA
3Department of Mathematical Sciences, Georgia Southern University, Statesboro, USA
Email: *farroyo@fmarion.edu
Copyright © 2013 Fangjun Arroyo et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 26, 2013; revised November 26, 2013; accepted December 2, 2013
Keywords: Compressed Sensing; Gaussian Sparse Signals; l1-Minimization; Reweighted l1-Minimization; l1; Greedy Algorithm Generalized l1 Greedy Algorithm
ABSTRACT
The generalized l1 greedy algorithm was recently introduced and used to reconstruct medical images in computerized tomography in the compressed sensing framework via total variation minimization. Experimental results showed that this algorithm is superior to the reweighted l1-minimization and l1 greedy algorithms in reconstructing these medical images. In this paper the effectiveness of the generalized l1 greedy algorithm in finding random sparse signals from underdetermined linear systems is investigated. A series of numerical experiments demonstrate that the generalized l1 greedy algorithm is superior to the reweighted l1-minimization and l1 greedy algorithms in the successful recovery of randomly generated Gaussian sparse signals from data generated by Gaussian random matrices. In particular, the generalized l1 greedy algorithm performs extraordinarily well in recovering random sparse signals with nonzero small entries. The stability of the generalized l1 greedy algorithm with respect to its parameters and the impact of noise on the recovery of Gaussian sparse signals are also studied.
1. Introduction
In signal processing one wants to reconstruct a signal from highly incomplete sets of linear measurements of the signal, that is, the number of measurements is much smaller than the dimension of the signal. More precisely, assuming  with
with , one wants to reconstruct an unknown signal
, one wants to reconstruct an unknown signal  from a set of m measurements b = Ax0. This requires one to solve the system of linear equations Ax = b (1)
from a set of m measurements b = Ax0. This requires one to solve the system of linear equations Ax = b (1)
to determine the solution that is exactly equal to x0. Since system (1) is consistent and underdetermined, it has infinitely many solutions making it difficult to find the correct solution x0. In many actual applications, such as image reconstruction and decoding, however, the signal one wants to reconstruct is known to be sparse (or nearly sparse) in the sense that its coefficients in some orthonormal basis are mostly zero (or approximately zero). The theory of compressed sensing [1-5] reveals that signals that have sparse representations can be reconstructed with high precision from far fewer measurements than the dimension of the signal itself. In fact, if the columns of A are chosen from a suitable distribution and the signal is sufficiently sparse, then the signal can be exactly recovered by solving the following standard l1-norm minimization problem:
 (2)
(2)
where . This optimization problem of a convex objection function can be solved effectively and it has broad applications [6-10]. But the iterative l1-minimization method has a shortcoming in finding the sparsest solution. Since the larger entries of x in each iteration skew the l1-norm, they are more heavily penalized in the l1-minimization process. To address this imbalance, weighted algorithms were introduced to reduce the influence of the larger entries. Two major algorithms designed for this purpose are the reweighted l1-minimization and l1 greedy algorithms [11,12].
. This optimization problem of a convex objection function can be solved effectively and it has broad applications [6-10]. But the iterative l1-minimization method has a shortcoming in finding the sparsest solution. Since the larger entries of x in each iteration skew the l1-norm, they are more heavily penalized in the l1-minimization process. To address this imbalance, weighted algorithms were introduced to reduce the influence of the larger entries. Two major algorithms designed for this purpose are the reweighted l1-minimization and l1 greedy algorithms [11,12].
Suppose that  is the sequence of vectors generated by l1-minimization. In the k-th iteration of the reweighted l1-minimization method [11], one minimizes
is the sequence of vectors generated by l1-minimization. In the k-th iteration of the reweighted l1-minimization method [11], one minimizes  instead of
instead of  in (2), where
in (2), where
 (3)
(3)
Observe that the weights in (3) are roughly inversely proportional to the sizes of the entries of the previous iterate xk−1. So the larger entries are weighted down to rectify their undue influence in the next iteration of the l1-minimization process. Numerical experiments [11] have indicated that the reweighted l1-minimization recovers random sparse signals with a much higher probability than the standard l1-minimization in (2). The reweighted l1-minimization algorithm has been extensively studied in recent years. The lq-minimization problem, 0 < q ≤ 1, was discussed and implemented using the reweighted l1-minimization scheme [13,14]. A two-step reweighted l1-minimization was introduced to improve the recovery of sparse signals [15], and a reweighted l1- minimization for a nonuniform sparsity model was proposed [16]. The performance of the reweighted l1-minimization with noisy data was also rigorously analyzed [17], and some convergence conditions of reweighted l1-minimization for a special family of measurement matrices were studied [18].
In the l1 greedy algorithm [12], instead of using variable weights as in (3) the weights are set to a fixed small constant ![]() for entries whose magnitude is above a certain threshold and to 1 for the other entries. This threshold is lowered after each iteration so that more and more large entries are weighted down by
for entries whose magnitude is above a certain threshold and to 1 for the other entries. This threshold is lowered after each iteration so that more and more large entries are weighted down by ![]() in each subsequent iteration step. More precisely, the weights
in each subsequent iteration step. More precisely, the weights  in the k-th iteration of the l1 greedy algorithm are defined by
in the k-th iteration of the l1 greedy algorithm are defined by

where , x0 is generated by the standard l1-minimization,
, x0 is generated by the standard l1-minimization, 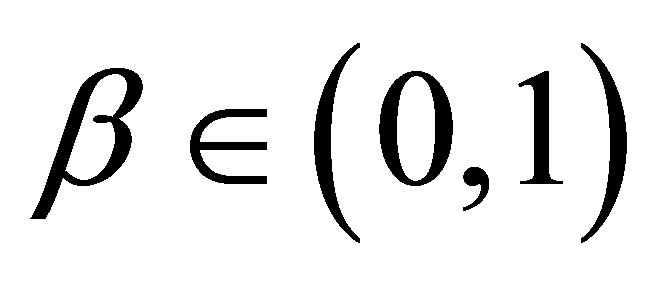 and
and . Numerical experiments showed that the l1 greedy algorithm outperforms both the unweighted and reweighted l1-minimization algorithms in recovering random sparse signals [12,19].
. Numerical experiments showed that the l1 greedy algorithm outperforms both the unweighted and reweighted l1-minimization algorithms in recovering random sparse signals [12,19].
A generalized l1 greedy algorithm in the compressed sensing framework was recently introduced by the authors of [20]. The new algorithm not only incorporates the threshold feature of the l1 greedy algorithm to counteract the influence of large entries but also assigns significantly large weights to the smallest nonzero entries to speed up the identification of nonzero entries. Moreover, in contrast to the l1 greedy algorithm where the remaining entries are assigned a neutral weight, the remaining entries in the generalized l1 greedy algorithm receive weight roughly inversely proportional to their magnitudes as in the reweighted l1-minimization algorithm. Thus the generalized l1 greedy algorithm not only incorporates features of both the l1 greedy and reweighted l1-minimization algorithms but also enhances the impact of the small entries in the l1-minimization process.
Generalized l1 greedy algorithm
1) Generate x0 by the reweighted l1-minimization;
2) For k = 1 to kmax;
a) Update the weight matrix Wk; where

b) Solve weighted l1-minimization problem:

c) Return if a stopping criterion is met.
In [20] the generalized l1 greedy algorithm was applied to the problem of reconstructing essentially piecewise constant medical images in computerized tomography (CT) in the compressed sensing framework via total variation minimization. Tested with the Shepp-Logan phantom and a real cardiac CT image, the generalized l1 greedy algorithm was shown to perform better than the reweighted l1-minimization and l1 greedy algorithms. In particular, it was observed that in the context of reconstructing these two images the generalized l1 greedy algorithm was superior to the others at distinguishing small gradients. However, to show that the generalized l1 greedy algorithm is truly superior to the other two algorithms at detecting small entries in general we should compare the performance of the three algorithms in recovering random sparse signals. So in this paper, following [11,12], we present a series of rigorous numerical studies of the performance of the generalized l1 greedy algorithm in the general setting of Gaussian random matrices A and random sparse signals x. The rest of this paper is organized as follows. In Section 2, the relative frequencies of successful recovery of random Gaussian sparse signals for the reweighted l1-minimization, l1 greedy, and generalized l1 greedy algorithms are compared. Section 3 presents the stability of the generalized l1 greedy algorithm with respect to its parameters. Section 4 studies the performance of the generalized l1 greedy algorithm on noisy data. Section 5 shows that the generalized l1 greedy algorithm is better at detecting smaller entries in the general setting than the other two algorithms. Section 6 concludes with a brief summary of the generalized l1 greedy algorithm and the results.
2. Relative Frequency of Success in Recovering Gaussian Sparse Signals
In our first experiment we want to determine how well each of the three algorithms can recover random Gaussian sparse signals from random Gaussian measurements b = Ax. Following the same approach taken in [11], we implement each of the three algorithms in MATLAB and invoke the l1eq-pd solver from the l1-MAGIC software package developed by E. Candes and J. Romberg (available at www.l1-magic.org). We set m = 128 and n = 256. For each trial, a random matrix  with i.i.d. Gaussian entries is selected and its columns are normalized. A random k-sparse signal
with i.i.d. Gaussian entries is selected and its columns are normalized. A random k-sparse signal  is also selected in such a way that the k nonzero positions are randomly distributed and the nonzero components satisfy the standard Gaussian distribution
is also selected in such a way that the k nonzero positions are randomly distributed and the nonzero components satisfy the standard Gaussian distribution . We run 150 trials for each sparsity level k between 50 and 90. The total number of iterations (excluding the initial l1-minimization step) for each of the three algorithms is set to 16. For the generalized l1 greedy algorithm we start with 4 iterations of the reweighted l1-minimization. The criterion for successful recovery for all three algorithms is set to
. We run 150 trials for each sparsity level k between 50 and 90. The total number of iterations (excluding the initial l1-minimization step) for each of the three algorithms is set to 16. For the generalized l1 greedy algorithm we start with 4 iterations of the reweighted l1-minimization. The criterion for successful recovery for all three algorithms is set to
 where x is the reconstruction of x0 by the algorithm. The parameters chosen for the three algorithms are listed as follows:
where x is the reconstruction of x0 by the algorithm. The parameters chosen for the three algorithms are listed as follows:
1) In the reweighted l1-minimization: .
.
2) In the l1 greedy algorithm: ;
; ; others are the same as in 1).
; others are the same as in 1).
3) In the generalized l1 greedy algorithm: ; s = 0.8;
; s = 0.8; ; others are the same as in 2).
; others are the same as in 2).
The settings in this section will be used throughout the paper unless changes are explicitly stated otherwise.
The output of this experiment is presented in Figure 1. As one can see from the graph, for a fixed sparsity level k the probability of successful recovery of a k-sparse signal by the generalized l1 greedy algorithm is higher than in the both cases of the reweighted l1-minimization and l1 greedy algorithms. On average, the l1 greedy algorithm and the generalized l1 greedy algorithm recover about 14% and 18% more entries than the reweighted l1-minimization method, respectively, for 50 ≤ k ≤ 90. Furthermore, on average, the generalized l1 greedy algorithm recovers about 6% more entries than the l1 greedy algorithm.
3. Influence of the Parameters on Reconstruction Success
An empirical analysis of the reweighted l1-minimization

Figure 1. Improvements in recovering sparse solutions from the generalized l1 greedy algorithm when compared to the reweighted l1-minimization and l1 greedy algorithms.
algorithm determined that the algorithm is robust with respect to ![]() (chosen from a suitable range) and that much of the improvement in recovery comes from the first few reweighting iterations [11]. We performed a similar analysis of the generalized l1 greedy algorithm, and our results indicate that the algorithm is stable with respect to each of its parameters (within a certain range of values). We illustrate this behavior with the parameter
(chosen from a suitable range) and that much of the improvement in recovery comes from the first few reweighting iterations [11]. We performed a similar analysis of the generalized l1 greedy algorithm, and our results indicate that the algorithm is stable with respect to each of its parameters (within a certain range of values). We illustrate this behavior with the parameter ![]() using the same settings as in Section 2 for the remaining parameters. From Figure 2 one can see that the algorithm is fairly stable for the following values of
using the same settings as in Section 2 for the remaining parameters. From Figure 2 one can see that the algorithm is fairly stable for the following values of![]() : 0.2; 0.3; 0.4. Our experimental results also show that the algorithm is very robust with respect to
: 0.2; 0.3; 0.4. Our experimental results also show that the algorithm is very robust with respect to  for
for  and fairly robust with respect to s and
and fairly robust with respect to s and  for values between 0.7 and 0.9. It is also evident from Figure 3 that the number of iterations kmax of the generalized l1 greedy algorithm has minimal affect on the performance of the algorithm when kmax ≥ 10. So in practice only a few iterations are needed to achieve the best performance of the generalized l1 greedy algorithm.
for values between 0.7 and 0.9. It is also evident from Figure 3 that the number of iterations kmax of the generalized l1 greedy algorithm has minimal affect on the performance of the algorithm when kmax ≥ 10. So in practice only a few iterations are needed to achieve the best performance of the generalized l1 greedy algorithm.
4. Influence of Noise on Reconstruction Success
In real life applications measured data are often corrupted by a small amount of noise. Thus one needs to recover the original signal x0 from noisy data
 ;
;
where  is an unknown noise term. The signal-tonoise ratio (SNR) in dB is defined by
is an unknown noise term. The signal-tonoise ratio (SNR) in dB is defined by
 where b = Ax0 is noise-free data. In this section we show how white Gaussian noise at SNR levels 40 dB and 60 dB, respectively, affect the performance of the generalized l1 greedy algorithm. We also compare the performance of the reweighted l1-minimization, l1 greedy, and generalized l1 greedy algorithms on noisy data with an SNR of 60 dB. As in [12] the precision of recovery is set according to the noise level. More precisely, the criterion for successful recovery are taken to be
where b = Ax0 is noise-free data. In this section we show how white Gaussian noise at SNR levels 40 dB and 60 dB, respectively, affect the performance of the generalized l1 greedy algorithm. We also compare the performance of the reweighted l1-minimization, l1 greedy, and generalized l1 greedy algorithms on noisy data with an SNR of 60 dB. As in [12] the precision of recovery is set according to the noise level. More precisely, the criterion for successful recovery are taken to be  and
and  for noisy data with an SNR of 40 dB and with an SNR of 60 dB, respectively. All the other settings are the same as in Section 2. Figure 4 shows that the performance of the generalized l1 greedy algorithm is very robust with respect to noise at an SNR level 60 dB and fairly robust with respect to noise at an SNR level 40 dB for 30 ≤ k ≤ 90. Figure 5 compares the performance of the three algorithms on noisy data with an SNR of 60 dB. Clearly, the generalized l1 greedy algorithms outperform the other two algorithms. Moreover, for noisy data with an SNR of 60 dB, on average, the generalized l1 greedy algorithm recovers about 17% more entries than the reweighted l1-minimization algorithm and about 5% more entries than the l1 greedy algorithm for 50 ≤ k ≤ 90.
for noisy data with an SNR of 40 dB and with an SNR of 60 dB, respectively. All the other settings are the same as in Section 2. Figure 4 shows that the performance of the generalized l1 greedy algorithm is very robust with respect to noise at an SNR level 60 dB and fairly robust with respect to noise at an SNR level 40 dB for 30 ≤ k ≤ 90. Figure 5 compares the performance of the three algorithms on noisy data with an SNR of 60 dB. Clearly, the generalized l1 greedy algorithms outperform the other two algorithms. Moreover, for noisy data with an SNR of 60 dB, on average, the generalized l1 greedy algorithm recovers about 17% more entries than the reweighted l1-minimization algorithm and about 5% more entries than the l1 greedy algorithm for 50 ≤ k ≤ 90.

Figure 2. Stability of the generalized l1 greedy algorithm with respect to the parameter α.

Figure 3. Effect of the number of iterations on the performance of the generalized l1 greedy algorithm.

Figure 4. Performance of the generalized l1 greedy algorithm with noisy data with an SNR of 40 dB and 60 dB, respectively.

Figure 5. Improvements in recovering sparse solutions with noisy data with an SNR of 60 dB from the generalized l1 greedy algorithm when compared to the reweighted l1-minimization and l1 greedy algorithms.
5. Reconstruction of Sparse Signals Containing Nonzero Small Entries
It is known that the l1 greedy algorithm outperforms the reweighted l1 minimization algorithm in finding spare signals [12,19]. However, the reweighted l1-minimization algorithm was designed to help speed up the detection of small entries [11]. The generalized l1 greedy algorithm of [20], which incorporates features of both algorithms, should have the performance advantage of the l1 greedy algorithm while enhancing the power of the reweighted l1-minimization algorithm in detecting small entries. In fact, the generalized l1 greedy algorithm appears to be superior to the other two algorithms in distinguishing small gradients in the task of reconstructing images via total variation minimization [20]. In this section we want to see how well the generalized l1 greedy algorithm would perform in recuperating random sparse signals with a guaranteed percentage of small entries. More precisely, in our last experiment we want to determine the extent to which the ratio of very small entries in the sparse signals affects the probability of successful recovery by each of the algorithms under consideration. The entries of the sparse signal in each trial are obtained from a mixed Gaussian distribution as follows: a random 30% of the entries are generated using a Gaussian distribution with mean 0 and standard deviation 0.01 while the remaining 70% of the entries are generated using the standard Gaussian distribution . We need to fine tune the generalized l1 greedy algorithm to make it most efficient at detecting the small entries in the range we set. Experimental trials show that setting
. We need to fine tune the generalized l1 greedy algorithm to make it most efficient at detecting the small entries in the range we set. Experimental trials show that setting  results in the best performance. The values of the other parameters are left unchanged. We then run 150 trials for each sparsity level k, 50 ≤ k ≤ 105, and set the criterion for successful recovery to
results in the best performance. The values of the other parameters are left unchanged. We then run 150 trials for each sparsity level k, 50 ≤ k ≤ 105, and set the criterion for successful recovery to . As one can see from Figure 6" target="_self"> Figure 6, the generalized l1 greedy algorithm vastly outperforms both the reweighted l1-minimization and the l1 greedy algorithms in recovering sparse solutions containing a few nonzero small entries. Moreover, on average, the generalized l1 greedy algorithm recovers 32% more entries than the reweighted l1-minimization algorithm and 11% more entries than the l1 greedy algorithm for 50 ≤ k ≤ 105.
. As one can see from Figure 6" target="_self"> Figure 6, the generalized l1 greedy algorithm vastly outperforms both the reweighted l1-minimization and the l1 greedy algorithms in recovering sparse solutions containing a few nonzero small entries. Moreover, on average, the generalized l1 greedy algorithm recovers 32% more entries than the reweighted l1-minimization algorithm and 11% more entries than the l1 greedy algorithm for 50 ≤ k ≤ 105.
6. Conclusion
Our statistical experiments indicate that the generalized l1 greedy algorithm outperforms the reweighted l1-minimization and l1 greedy algorithms in recovering random sparse signals from random Gaussian measurements. In fact, the generalized l1 greedy algorithm recovers more entries than the other two algorithms. Moreover, the performance of the algorithm is robust with respect to its parameters and to noisy data at different noise levels. Finally, the generalized l1 greedy algorithm performs

Figure 6. Improvements in recovering sparse solutions with a mixed Gaussian distribution from the generalized l1 greedy algorithm when compared to the reweighted l1-minimization and l1 greedy algorithms.
extremely well in detecting small entries of unknown sparse signals thereby dramatically speeding up their recovery via l1-minimization. It is expected that more details of signals could be recovered by using the generalized l1 greedy algorithm without extra cost.
7. Acknowledgements
F. Arroyo was supported by a faculty research grant from Francis Marion University. X. Li and J. Zhu were partially supported by a Faculty Research Award and a COSM Interdisciplinary Pilot Fund from Georgia Southern University.
REFERENCES
- E. Candes, J. Romberg and T. Tao, “Stable Signal Recovery from Incomplete and Inaccurate Information,” Communications on Pure and Applied Mathematics, Vol. 59, No. 8, 2005, pp. 1207-1233. http://dx.doi.org/10.1002/cpa.20124
- E. Candes, J. Romberg and T. Tao, “Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information,” IEEE Transactions on Information Theory, Vol. 52, No. 2, 2006, pp. 489-509. http://dx.doi.org/10.1109/TIT.2005.862083
- E. Candes and T. Tao, “Near Optimal Signal Recovery from Random Projections: Universal Encoding Strategies?” IEEE Transactions on Information Theory, Vol. 52, No. 12, 2006, pp. 5406-5425. http://dx.doi.org/10.1109/TIT.2006.885507
- E. Candes and M. Wakin, “An Introduction to Compressive Sampling,” IEEE Signal Processing Magazine, Vol. 25, No. 2, 2008, pp. 21-30. http://dx.doi.org/10.1109/MSP.2007.914731
- D. Donoho, “Compressed Sensing,” IEEE Transactions on Information Theory, Vol. 52, No. 4, 2006, pp. 1289- 1306. http://dx.doi.org/10.1109/TIT.2006.871582
- S. Chen, D. Donoho and M. Saunders, “Atomic Decomposition by Basis Pursuit,” SIAM Journal on Scientific Computing, Vol. 20, No. 1, 1998, pp. 33-61. http://dx.doi.org/10.1137/S1064827596304010
- D. Donoho and B. F. Logan, “Signal Recovery and the Large Sieve,” SIAM Journal on Applied Mathematics, Vol. 52, No. 2, 1992, pp. 577-591. http://dx.doi.org/10.1137/0152031
- D. Donoho and P. B. Stark, “Uncertainty Principles and Signal Recovery,” SIAM Journal on Applied Mathematics, Vol. 49, No. 3, 1989, pp. 906-931. http://dx.doi.org/10.1137/0149053
- F. Santosa and W. Symes, “Linear Inversion of BandLimited Reflection Seismograms,” SIAM Journal on Scientific and Statistical Computing, Vol. 7, No. 4, 1986, pp. 1307-1330. http://dx.doi.org/10.1137/0907087
- R. Tibshirani, “Regression Shrinkage and Selection via the Lasso,” Journal of the Royal Statistical Society: Series B, Vol. 58, 1996, pp. 267-288.
- E. J. Candes, M. B. Wakin and S. P. Boyed, “Enhancing Sparsity by Reweighted l1 Minimization,” Journal of Fourier Analysis Applications, Vol. 14, No. 5-6, 2008, pp. 877-905. http://dx.doi.org/10.1007/s00041-008-9045-x
- I. Kozlov and A. Petukhov, “Sparse Solutions of Underdetermined Linear Systems,” Handbook of Geomathematics, Springer, New York, 2010, pp. 1243-1260. http://dx.doi.org/10.1007/978-3-642-01546-5_42
- S. Foucarts and M. J. Lai, “Sparsest Solutions of Underdetermined Linear Systems via lq-Minimization for 0 < q ≤ 1,” Applied and Computational Harmonic Analysis, Vol. 26, No. 3, 2009, pp. 395-407. http://dx.doi.org/10.1016/j.acha.2008.09.001
- M. J. Lai, “On Sparse Solutions of Underdetermined Linear Systems,” Journal of Concrete and Applicable Mathematics, Vol. 8, 2010, pp. 296-327.
- A. Khajehnejad, W. Xu, S. Avestimher and B. Hassibi, “Improved Sparse Recovery Thresholds with Two-Step Reweighted l1-Minimization,” IEEE International Symposium on Information Theory Proceedings, 2010.
- A. Khajehnejad, W. Xu, S. Avestimher and B. Hassibi, “Analyzing Weight l1-Minimization for Sparse Recovery with Nonuniform Sparse Models,” IEEE Transaction on Signal Processing, Vol. 59, No. 5, 2011, pp. 1985-2001. http://dx.doi.org/10.1109/TSP.2011.2107904
- D. Needell, ”Noisy Signal Recovery via Iterative Reweighted l1-Minimization,” Proceedings of 43rd Annual Asilomar Conference on Signals, Systems, and Computers, 2009, pp. 113-117.
- Y. B. Zhao and D. Li, “Reweighted l1-Minimization for Sparse Solutions to Underdetermined Linear Systems,” SIAM Journal on Optimization, Vol. 22, No. 3, 2012, pp. 1065-1088. http://dx.doi.org/10.1137/110847445
- A. Petukhov and I. Kozlov, ”Fast Implementation of l1 Greedy Algorithm,” Recent Advances in Harmonic Analysis Applications, Springer Proceedings in Mathematics & Statistics, Vol. 25, 2013, pp. 317-326. http://dx.doi.org/10.1007/978-1-4614-4565-4_25
- J. Zhu and X. Li, “A Generalized l1 Greedy Algorithm for Image Reconstruction in CT,” Applied Mathematics and Computation, Vol. 219, No. 10, 2013, pp. 5487-5494. http://dx.doi.org/10.1016/j.amc.2012.11.052
NOTES
*Corresponding author.

