Received 15 March 2015; accepted 17 April 2015; published 20 April 2015

ABSTRACT

Simulation experiments with different stochastic models were conducted to investigate the long term characteristics of rainfall in Saudi Arabia using selected Autoregressive Moving Average (ARMA) models. The results of the study indicated that the ARMA models were able to capture the long term statistics for one of the rainfall records investigated (Surat Obeida). However, the other rainfall record investigated in this study (Malaki) was characterized with a slow and long decaying structure and a high Hurst coefficient indicating the possibility of non-stationarity of the data. Trend analysis (Pettitt test) of the data revealed that a break point or a shift in the record happened around 1983 at Malaki. As a result, ARMA models should not be used in modeling the rainfall data at that station.

Keywords:

Rainfall Modeling, Hurst Coefficient, ARMA, Trend Analysis

1. Introduction

Stochastic modeling of hydrologic time series has been widely used for planning and management of water resources systems. Stochastic models are used in operational hydrology to generate synthetic time series which exhibit similar statistical characteristics as the observed data. One of the crucial problems in stochastic modeling of hydrologic time series is to find a model which is capable of preserving the historical statistical characteristics that affect the variability of the data. Furthermore, the model should be capable of reproducing certain statistics that are related to the intended use of the model [1] . Generally, the properties of a process include the mean, variance, skewness, and the correlation structure of the data.

Additional properties related to the long term characteristics such as storage and drought related statistics may also be included, depending on the particular problem at hand [1] . In this era of possible adverse effects of climate change, preservation of such long term characteristics is important. The “Hurst” behavior of a time series is one of these characteristics, which is related to the long term persistence of that series [2] . Besides persistence, other reasons could explain the Hurst behavior such as the non-stationarity in the mean, which could be one of manifestation of the effects of climate change [2] [3] .

Rehman [4] analyzed rainfall data at 10 locations in Saudi Arabia and showed that the Hurst exponent value for all stations was >0.5, indicating the existence of a persistence behavior of the rainfall data in Saudi Arabia.

Elfeki, Al-Amri, and Bahrawi [5] used a spectral density function (SDF) approach to analyze annual rainfall signals in the southwestern part of the Kingdom of Saudi Arabia. Results showed that multiple cyclic components with significant variances existed and that a common cycle of 26 years existed in all annual rainfall data studied [5] .

Almazroui, Nazrul Islam, Athar, Jones and Ashfaqur Rahman [6] compared temperature and rainfall data from 3 gridded datasets (CRU, CMAP and TRMM) with the observed temperature and rainfall data for Saudi Arabia. Results showed that the observed annual rainfall showed a significant decreasing trend (47.8 mm per decade) in the last 15 years with a relatively large inter-annual variability, while the maximum, mean and minimum temperatures had increased significantly at a rate of 0.71˚C, 0.60˚C, and 0.48˚C per decade, respectively [6] .

The objective of this study is to investigate the use of ARMA models in modeling and simulation of annual rainfall data in Saudi Arabia and their ability to capture the long term statistics observed in the historical records. In this paper, three univariate (single site) models will be used in this study, namely, AR (1), ARMA (1,1), and ARMA (2,1) models.

2. Materials and Methods

2.1. Data Used

The historical annual rainfall amounts in, two stations (Surat Obeida and Malaki) in Saudi Arabia were used in this study. The data used for Surat Obeida was for 30 years for the period of 1981 through 2010 while at Malaki, 27 years of data (1967-1993) was used. It is noted here that the record at Malaki has data between 2001 and 2010 but missing records for the period of 1994-2000. As a result, it was decided to use only the continuous record (1967-1993) in this study. Figure 1 shows a time series plot of the annual rainfalls at the two stations.

2.2. Models Used

The univariate Autoregressive Moving average (ARMA) model may be written as 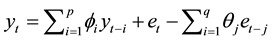[1] :

(1)

where represents the standardized process for year t, it has a mean = 0 and variance 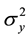and is normally distributed; is the uncorrelated noise term with mean = 0 and variance 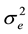and is also normally distributed. are the autoregressive parameters; 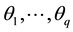are the moving average parameters. For example, for p = q = 1, the ARMA (1,1) model becomes:

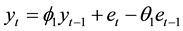(2)

2.3. Long Term Related Statistics

Consider the above time series (with length N) 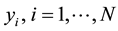and a subsample 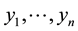with n < N. If one forms the sequence of partial sum S_i as:

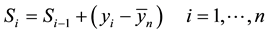(3)

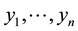where and is the sample mean of, then, the adjusted range 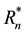and the rescaled adjusted range can be calculated as:

(4)

And

(5)

In which is the standard deviation of. Likewise, the Hurst coefficient (K) is then estimated by [7] :

(6)

For the series and for a demand level = (the mean), a deficit with duration (L) occurs when consecutively during one or more years until again. Assume that m deficits occur in a given sample, then the maximum deficit duration, or longest drought (D), is given by [7] :

(7)

Similarly, a surplus with duration (P) occurs when consecutively during one or more years until again. Assume that j surpluses occur in a given sample, then the longest surplus duration (U) is given by [7] :

(8)

2.4. Simulation Experiments

Monte Carlo simulation experiments were conducted with AR (1), ARMA (1,1), and ARMA (2,1). The purpose of such experiments were to test the capability of such models to preserve the long term statistics of the historical rainfall data used in this study. A software package, Stochastic Analysis Modeling and Simulation (SAMS), was used in this study to conduct the simulation experiments [8] .

To apply and use the models mentioned above, the observed data must be normally distributed. The analysis of the skewness coefficient revealed that the observed data at Surat Obeida is not normal. SAMS provide option to transform the data in order to normalize it. Logaritmic, Box-Cox, and power transformations options are available in SAMS. The data at Surat obeida was normalized by using a logarithmic transformation. The skewness coefficient of the transformed data revealed that the transformed data was Norma. The data at Malaki was shown to be Normal and no transformation was done for Malaki.

Each ARMA model was then fitted to the normalized data. Simulation experiments were then conducted by generating synthetic time series data using the fitted models. In each experiment 100 samples, each with length equal to the historical length of the series (i.e. 30 years for Surat Obeida and 27 for Malaki) were generated from the fitted models. The average statistics calculated from these generated series were then compared with the historical statistics. These include the annual Correlogram, longest drought, longest surplus, and Hurst coefficient.

3. Results

The autocorrelogram of the historical annual data at Surat Obeida as well as the genertaed autocorrelogram of AR (1), ARMA (1,1), and ARMA (2,1) models are shown in Figures 2-4 respectively. Results indicate that the autocorrelogram was well preserved by all three models. Table 1 shows the results of the simulation experiments in preserving the long term statistics of the historical data. The three models were capable of reproducing the historical Hurst coefficient. The models, in general, also performed well in preserving the longest drought and the longest surplus.

Results at Malaki were not as good. All three models underestimated the historical autocorrelogram as shown in Figures 5-7. Table 1 shows the results of the simulation experiments in preserving the long term statistics. These statistics were not well preserved for at Malaki. The hurst coefficient was consistently underestimated by all the models used in this study.

The Pettit test was used to detect possible change points in the annual rainfall data at the two stations used in this study. Results for Malaki revealed that a change point (shift) in the data happens around 1983, with a 95% and 99% significance levels, as shown in Figure 8. On the other hand, for Surat Obeida, the pettitt test revealed that no break point exist in the record.

4. Discussion

Auto regressive moving average (ARMA) models have been widely used in stochastic hydrology to model annual time series where the mean, variance, and the correlation structure do not depend on time. These models are capable of preserving the basic statistical characteristics of annual historical time series such as the mean and variance and also can preserve the long term related statistics [3] . However, the simulation experiments in this study revealed that the tested ARMA models did not perform well at Malaki, but performed reasonably well at Surat Obeida.

A time series Hurst Coefficient in the range 0.5 - 1 would indicate a series with a long decaying positive autocorrelation, meaning both that a high value will probably be followed by another high value resulting in having periods or clusters of high values [9] . A value in the range 0 - 0.5 indicates a switching behavior between high and low values, meaning that a high value will probably be followed by a low value and vice versa and a value of 0.5 indicates a completely uncorrelated behavior [9] . The historical autocorrelgram at Malaki is characterized by slow long decaying correlation structure whereas the autocorrelogram at Surat Obeida is fast decaying type. The Hurst coefficient at Malaki was high (K = 0.88) indicating a strong peristance features. As was shown earlier, results of the pettit test indicate an existance of a break point or a shift in the record that could have happened around 1983 at Malaki. This could suggest the possibility of non-stationarity of the historical record of Malaki.

5. Conclusions

The ARMA models were used for modeling and simulation of rainfall in arid and semi-arid regions. The ARMA models were able to preserve the long term statistics at Surat Obeida, but failed to do so at Malaki. Malaki historical data reveled a slow and long decaying structure and a high Hurst coeficient indicating the possibility of non-stationarity of the data. Pettitt test revealed that a break point or a shift in the record of Malaki happened around 1983, which could indicate that the data were non-stationary. Thus, it is recommended that ARMA models should not be used in modeling the annual rainfall at Malaki.

Finally, future investigation of other stochastic models that are capable of preserving long term characteristics is needed.

Acknowledgements

The researcher would like to extend his gratitude and appreciation to Dr. Mohammed Al Zahrani, Associate Professor of Civil Engineering at King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia for providing the historical rainfall data.

References