Crystal Structure Theory and Applications
Vol.05 No.02(2016), Article ID:66438,18 pages
10.4236/csta.2016.52003
Ab Initio Calculations on Structural, Electronic and Optical Properties of ZnO in Wurtzite Phase
Rita John*, S. Padmavathi
Department of Theoretical Physics, University of Madras, Chennai, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 March 2016; accepted 10 May 2016; published 13 May 2016
ABSTRACT
Self-consistent ab initio calculations are performed on the structural, electronic and optical pro- perties of wurtzite ZnO. The Full Potential Linearized Augmented Plane Wave (FP-LAPW) method is applied to solve the Kohn-Sham equations. Results are obtained by using the PBE-GGA and mBJLDA exchange correlation potentials. The energy and charge convergence have been examined to study the ground state properties. The band structure and Density of States (DOS) diagrams are plotted from the calculated equilibrium lattice parameters. The general profiles of the optical spectra and the optical properties, including the real and imaginary part of dielectric function, reflectivity, refractive index, absorption co-efficient, electron energy loss function and optical conductivity of wurtzite ZnO under ambient conditions are discussed. The optical anisotropy is studied through the calculated optical constants, namely dielectric function and refractive index along three different crystallographic axes.
Keywords:
w-ZnO, DFT, mBJLDA, Optical Properties

1. Introduction
Zinc oxide (ZnO) is the most promising candidate of II-VI semiconductor family due to its vital applications in various fields. It has attracted much interest of the research community for its electronic properties such as a wide band gap, ~3.34 eV and a large exciton binding energy, 60 meV [1] . It is ample in nature, environmentally friendly and even biocompatible. In addition, ZnO occupies an ideal place in optical and photonic devices, directly or as a substrate for the growth of other semiconductors such as GaN and SiC [2] . Exploration on optical properties and refractive index of ZnO were studied many decades ago [3] - [12] . Its superior electronic, optical and piezoelectric properties make it a noticeable candidate for applications in visible and ultraviolet light emitters, transparent field-effect transistors, ultraviolet nanolasers, photodetectors, solar cells, surface acoustic wave devices, gas sensors and piezoelectric devices [13] - [17] . The technological importance of ZnO makes the researchers to do continuous work on it and to achieve more potential utilization in optical devices.
ZnO crystallizes in three different structures such as hexagonal wurtzite (B4), cubic zincblende (B2), and cubic rocksalt (B1). Hexagonal wurtzite structure of ZnO is the most stable structure under ambient conditions, which belongs to the space group P63mc. Each zinc atom is surrounded by four oxygen atoms, which are located at the corner of a regular tetrahedron and vice versa [18] . Considerable studies have been done on structural and optical properties of ZnO in wurtzite phase [18] - [23] . Schleife et al. [19] performed ab initio calculations of optical and energy loss spectra of quasi particle ZnO with GGA+U scheme and scissor operator using VASP. Linear and non-linear optical response of ZnO has been studied with PW92, LDA scheme and scissor operator using ABINIT code by Fanjie Kong et al. [20] . The impact of pressure on structural transitions is also studied using band structure calculation as a tool and the optical properties at high-pressure phases of ZnO have also been reported with GGA using CASTEP code by Jian Sun et al. [22] .
The theoretical interpretations of optical properties are very important, because the electronic structure has a large impression on optical and energy loss properties [19] . In the present work, we aim to give the theoretical insight of the structural, electronic and optical properties of ZnO in wurtzite phase with efficient mBJLDA potential using ab initio calculations. In Section 2, we give the computational details and brief description of the method of calculation. In Section 3, we discuss the results of present calculation. Finally, the conclusions are presented in Section 4.
2. Theoretical and Computational Details
First principle calculations are performed on structural, electronic and optical properties of wurtzite ZnO. To obtain reliable results, a highly accurate Full Potential Linearized Augmented Plane Wave (FP-LAPW) method is applied, as implemented in WIEN2k code based on Density Functional Theory (DFT) [25] [26] . The exchange correlation effect is treated using modified Becke-Johnson Local Density Approximation (mBJLDA) [27] [28] and Perdew-Burke-Ernzerhof-Generalized Gradient Approximation (PBE-GGA) [29] . It is a well- known fact that GGA underestimates the band gap value in semiconductors [20] [30] [31] and also locates the d and f orbitals in a poor manner. This is mainly due to the fact that GGA prescriptions have simple forms and are not amply flexible to accurately reproduce both the exchange―correlation energy and its charge derivative. To overcome this shortcoming, the mBJLDA potential is employed to study the structural, electronic and optical properties of ZnO in wurtzite structure. The mBJLDA potential not only provides better band gaps and also reasonably reproduces the reliable experimental ones for semiconductors and highly correlated electron system [31] .
In FP-LAPW method, the basis set is obtained by dividing the unit cell into non-overlapping spheres surrounding each atom and creating an interstitial region between them. The potential and the charge density are expanded by spherical harmonics inside the muffin-tin sphere and by plane wave basis set in the interstitial region of the unit cell. The equilibrium volume V0, bulk modulus B0, pressure derivative of bulk modulus 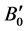 and the ground state energy E0 are determined by fitting the total energy versus the reduced and extended volume of the unit cell into third-order Birch-Murnaghan’s equation of state (EOS) [32] [33] . In the third-order Birch- Murnaghan’s equation of state (EOS), the total energy and pressure as a function of volume are given as,
and the ground state energy E0 are determined by fitting the total energy versus the reduced and extended volume of the unit cell into third-order Birch-Murnaghan’s equation of state (EOS) [32] [33] . In the third-order Birch- Murnaghan’s equation of state (EOS), the total energy and pressure as a function of volume are given as,
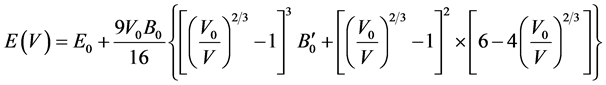 (1)
(1)
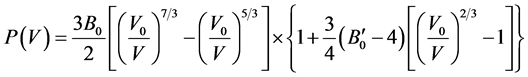 (2)
(2)
respectively. In these expressions, E0 is the total energy; V0 is the equilibrium volume; B0 is the bulk modulus at pressure P = 0; and 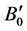 is the first derivative of the bulk modulus with respect to pressure.
is the first derivative of the bulk modulus with respect to pressure.
Geometry minimization is also done for obtaining the optimized positions. To achieve the energy convergence of the eigenvalues, the wave function in the interstitial regions is expanded in plane waves with a k cut-off, kmax = 7.0/RMT, where RMT denotes the smallest atomic sphere radius (muffin-tin radius) and kmax denotes the magnitude of the largest k-vector in the plane wave expansion. The valence wave functions inside the muffin-tin sphere are expanded up to lmax = 10, while the charge density is Fourier expanded up to Gmax = 12 (Ryd)1/2. The RMT values are 1.75 and 1.53 a.u. for Zn and O, respectively. A dense mesh of 1000 k points is used in the irreducible wedge of the brillouin zone. The self-consistent calculations are iterated till the total energy converges below 10−4 Ry and force converges below 1 mRy/a.u. Zn 3d, 4s and O 2s, 2p orbitals are considered as valence states and all lower-lying states are treated as core. The atomic positions are (1/3, 2/3, 0) (2/3, 1/3, 0.5) for Zn and (1/3, 2/3, 0.38) (2/3, 1/3, 0.88) for O, respectively. The volume optimization curve is shown in Figure 1.
3. Results and Discussion
3.1. Structural Properties
The ground state structural properties such as, equilibrium lattice parameters (a0 and c0), anion position parameter u (which governs the positions of oxygen ions), equilibrium volume (V0), bulk modulus (B0) and its pressure derivative (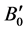 ) calculated are shown in Table 1. The present values are in good agreement with the experimental one [20] [34] and are also compared with other reported theoretical values [35] - [37] . Bulk modulus (B0) and its pressure derivative (
) calculated are shown in Table 1. The present values are in good agreement with the experimental one [20] [34] and are also compared with other reported theoretical values [35] - [37] . Bulk modulus (B0) and its pressure derivative (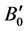 ) of ZnO are also in reasonable agreement with other reported theoretical values.
) of ZnO are also in reasonable agreement with other reported theoretical values.
3.2. Electronic Properties
3.2.1. Band Structure
The electronic properties of ZnO are discussed using the band structure, total density of states (TDOS) and partial density of states (PDOS) calculated with optimized values. Spin polarized and non-spin polarized calculations are performed using both mBJLDA and PBE-GGA potentials. The calculated band structure along the higher symmetry points Г-M-K-Г-A and higher symmetry directions Σ, Δ, Λ in the brillouin zone using mBJLDA
Figure 1. Total energy vs. volume.
Table 1. The equilibrium lattice parameters, a0 and c0, u parameter, volume V0, bulk modulus B0 and pressure derivative of bulk modulus 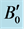 of w-ZnO.
of w-ZnO.
PW-present work; Exp.-experiment; Cal.-Calculations. [a] Exp. [34] ; [b] LCOA [35] ; [c] GGA [36] ; [d] PW92-LDA [20] ; [e]GGA [37] ; [f] PW91- GGA [38] .
and PBE-GGA approach are shown in Figure 2(a) and Figure 2(b), respectively.
The valence band maximum and the conduction band minimum are located at Г point, resulting in a direct band gap. The Eg using PBE-GGA and mBJLDA are 0.814 eV and 2.683 eV respectively. F. Tran and P. Blaha have reported the Eg of 0.75 eV and 2.68 eV using the LDA and mBJLDA potentials, respectively [28] . In the present study, similar generic nature is observed in the band structure of w-ZnO using mBJLDA and PBE-GGA. First valence band at Г locates between 0 and −1 eV in both the band structures obtained using mBJLDA and PBE-GGA. In the mBJLDA band structure, the second valence band at Г is located in the region −3 eV to −4 eV, and that using PBE-GGA, lies below −4 eV to −5 eV. Third/lower valence bands in mBJLDA band structure are located around −5 eV and that in PBE-GGA, are around −5.5 eV. The present study reveals an interesting shifting of the bands. Conduction band minimum is lowered by 2.7 eV in mBJLDA band structure, where as in PBE-GGA band structure the conduction band minimum is lowered by lesser than 1 eV. Higher conduction band shows more shifting which is around 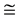 7 eV in mBJLDA, though in PBE-GGA the shift is around
7 eV in mBJLDA, though in PBE-GGA the shift is around  5 eV. Further, we also note that, shifting of lower valence band and higher conduction band are more, compared to that of conduction band minimum and the valence band maximum closer to the Fermi. The downward shifting of the valence and conduction bands, using PBE-GGA is more when compared to mBJLDA. Lower valence bands get more localized compared to upper valence band when PBE-GGA is used. The present Eg using mBJLDA shows better agreement with experimental values, which confirms that mBJLDA potential, is best suited for w-ZnO, compared to GGA and LDA. So, in the present study the further calculations such as electronic and optical properties of w-ZnO are done using mBJLDA and presented in the subsequent sections.
5 eV. Further, we also note that, shifting of lower valence band and higher conduction band are more, compared to that of conduction band minimum and the valence band maximum closer to the Fermi. The downward shifting of the valence and conduction bands, using PBE-GGA is more when compared to mBJLDA. Lower valence bands get more localized compared to upper valence band when PBE-GGA is used. The present Eg using mBJLDA shows better agreement with experimental values, which confirms that mBJLDA potential, is best suited for w-ZnO, compared to GGA and LDA. So, in the present study the further calculations such as electronic and optical properties of w-ZnO are done using mBJLDA and presented in the subsequent sections.
3.2.2. Total and Partial Density of States
Total and partial densities of states of w-ZnO are shown in Figures 3(a)-(c) for the energy range −8 eV to +10 eV. The first valence band is located between 0 to −3.5 eV and it comes from the admixture of O “p” state, Zn “p” state and a small amount of Zn “d” states. This mainly comes from the p-d hybridization between O “p” and Zn “d” states. The second valence band is located between −3.4 eV to −4.0 eV. This is predominantly from “d” states of Zn. The third valence band below −4 eV to −5.5 eV is the admixture of “d” and “p” states of Zn and “p” state of O. Figures 4(a)-(e) represent the partial density of states (PDOS) of s, p, d of Zn and s, p of O, respectively, using mBJLDA. This clearly shows the hybridization discussed above and nature of bonding. Figure 3(d) illustrates the total DOS of w-ZnO obtained by spin polarized calculation using mBJLDA. The spin up DOS is plotted in the positive region and spin down DOS is plotted in the negative region. There is no significant difference between the two spectra in spin polarized density of states of ZnO, (i.e.) the peaks in the DOS of spin up and spin down calculations are equal. It reveals that ZnO is non-magnetic in nature.
3.2.3. Charge Density Contour
We have investigated the electronic charge density contour of w-ZnO in (110) plane, to analyse nature of chemical bond between Zn and O atoms, as shown in Figure 5(a), Figure 5(b). Since there is a large difference in the electro negativity of Zn and O atom, charge transfer happens from Zn to O atoms. The calculated electron density of w-ZnO shows that charge density contour lines are spherical as well as sharing of electrons also appear which causes strong covalent interaction between Zn-O atoms. Thus w-ZnO has both ionic and covalent bonds.
Figure 2. (a) Calculated band structure of pure ZnO using mBJLDA and (b) PBE-GGA.
Figure 3. (a) Total density states; (b) (c) Partial density of states of ZnO using mBJLDA; (d) Total DOS of ZnO obtained by spin polarized calculation using mBJLDA.
Figure 4. Partial density of states of (a) s, (b) p, (c) d of Zn, (d) s, (e) p of O using mBJLDA.
Figure 5. (a) Electron density 3D plot of w-ZnO and (b) Electron density contour plot of w-ZnO with mBJLDA.
3.3. Optical Properties
Optical properties play an active role in the understanding of the nature of material and provide a clear picture for the usage of a material in opto electronic devices. It is generally known that the interaction of a photon with the electrons inthe system can be described in terms of time-dependent perturbations of the ground-state electronic states. Transitions between occupied and unoccupied states are originated by the electric field of the photon. The spectra resulting from these excitations can be described as a joint density of states between the valence and conduction bands. The optical response of a material to the electromagnetic field at all energy levels, can be described by means of complex dielectric function ɛ(ω) as,

where, ɛ1(ω) and ɛ2(ω) are real and imaginary part of the dielectric function. Real part of the dielectric function ɛ1(ω), means the dispersion of the incident photons by the material, while the imaginary part of the dielectric function ɛ2(ω), corresponds to the energy absorbed by the material. There are two contributions to complex dielectric function ɛ(ω), namely intraband and interband transitions. The contribution from intraband transitions is influential only for metals. The interband transitions can be further divided into direct and indirect transitions [20] . Here the indirect interband transitions is neglected, which include scattering of phonon and are expected to give only little contributions to ɛ(ω) [21] .
The imaginary part ɛ2(ω) of the dielectric function is calculated from the contribution of the direct interband transitions from the occupied to unoccupied states and the calculation is associated with the energy eigenvalue and energy wave functions, which are the direct output of band structure calculation. ɛ2(ω) can be calculated using the following expression [39] .

where, M is the dipole matrix; i and j are initial and final states respectively; fi is the Fermi distribution function for the ith state; Ei is the energy of electron in the ith state and ω is the frequency of the incident photon. Real part ɛ1(ω) of the dielectric function can be found from its corresponding ɛ2(ω) by Kramers-Kronig transformation in the form [39] [40]

where, P stands for the principle value of the integral.
Figure 6(a), Figure 6(b) illustrate the calculated result for the imaginary ɛ2(ω) and real ɛ1(ω) part of the dielectric function, respectively, for the electric field vector parallel and perpendicular to the crystallographic c-axis. Since w-ZnO has hexagonal symmetry, we need to calculate two different independent principle components for ɛ(ω) such as, ɛzz(ω) and ɛxx(ω) corresponding to light polarized parallel and perpendicular to c-axis. Due to this reason, all optical constants are compared together in two directions.
In Figure 6(a), we observed a shoulder at 3.7 eV in both ɛ1(ω)xx and ɛ1(ω)zz spectra, which falls to a first critical point at 2.68 eV. This is again showing the direct band gap nature of ZnO as discussed earlier in section 3.2.1 and as shown in Figure 2(a). The first critical point of ɛ2(ω) is 2.68 eV, which is close to the calculated band gap and also known as the fundamental absorption edge. This confirms the direct optical transitions, between the valence band maxima and the conduction band minima at Г. The prominent large peak in the spectra is situated at 11.7 and 13.3 eV for ɛ2(ω)xx and ɛ2(ω)zz respectively. There are two small humps in ɛ2(ω)xx spectrum, situated at 8.0 and 13.1 eV and one shoulder at 12.3 eV whereas in ɛ1(ω)zz spectrum there are three small humps located at 8.2, 11 and 12 eV. The transition between Zn 4s and O 2p orbitals may drive to the peak at around 8.0 eV. The peak at 11.0 eV is mainly from the transition between O 2p and Zn 3d orbitals. The peaks around 13 eV come from Zn 3d and O 2s states. These results are consistent with the other reported results [22] . We observed considerable anisotropy in the imaginary and real part of the dielectric function of w-ZnO in the range 8 - 13 eV, while they are isotropic in the lower energy region. This anisotropy in the optical properties is expected for low symmetry crystals [41] .
Figure 6. (a) Imaginary part of dielectric function ɛ2(ω) and (b) Real part of dielectric function ɛ1(ω) as a function of photon energy for pure ZnO with mBJLDA.
The static dielectric constant value (the value of the dielectric constant at zero energy) of ɛ1(0) is 2.8. A higher value of energy gap produces a smaller ɛ1(0), which can be explained on the basis of the Penn model [42] . From the knowledge of ɛ1(ω) and ɛ2(ω), all the other optical properties, such as, reflectivity R(ω), refractive index n(ω), extinction coefficient κ(ω), energy loss function L(ω), absorption coefficient α(ω) and optical conductivity σ(ω) can be calculated [22] [24] .

where, n is the real part of the complex refractive index (refractive index) and κ is the imaginary part of the refractive index (extinction co-efficient).



Figure 7(a), Figure 7(b) show the reflectivity and energy loss spectra of ZnO. The reflectivity is significantly
Figure 7. (a) Calculated reflectivity R(ω) and (b) energy loss function L(ω) as a function of photon energy for pure ZnO with mBJLDA.
enhanced after 13 eV. From the reflectivity spectra we observed, the anisotropy behaviour of w-ZnO is small up to the photon energy 10 eV. The reflectivity data of the present calculation are compared with other experimental data. The line shape of our calculated reflectivity spectra is in reasonable agreement with the previously measured reflectivity [43] . The theoretical spectra show much finer and pronounced peaks. The important reason for the difference between theoretical and experimental results about the peak positions is a possible strain in the sample [19] .
L(ω) is an important factor describing the energy loss of a fast moving electron in a material. The peaks in L(ω) spectra represent the characteristic combined with the plasma resonance and the corresponding frequency is the so-called plasma frequency (ωpl), above which the material shows the dielectric behaviour [ɛ1(ω) > 0], while below which the material exhibits the metallic property [ɛ1(ω) < 0]. The peaks in L(ω) spectra reveal that the point of transition from the metallic property to dielectric property for a material [22] . In addition the peaks of L(ω) also correspond to the trailing edges in the reflection spectra, for instance, the peaks of L(ω) for ZnO is around 9.91 and 12.8 eV corresponding to the abrupt reduction of R(ω) as shown in Figure 7(a).
Figure 8(a), Figure 8(b) show the refractive index and extinction co-efficient of ZnO. Refractive index of an optical medium is a dimensionless quantity that describes propagation of beam through that medium. The line shape of n(ω) spectra is similar as ɛ1(ω) due to relation
Birefringence is the optical property of a material having a refractive index that depends on the polarization and propagation direction of light. These optically anisotropic materials are said to be birefringent. The birefringence is quantified as the difference between the extraordinary and ordinary refractive indices, Δn(ω) = ne(ω) - no(ω), where ne(ω) is the index of refraction for an electric field oriented along the c-axis and no(ω) is the index of refraction for an electric field perpendicular to the c-axis [20] . Birefringence is important only in the non- absorbing region, which is below the energy gap. The static value of ne(ω) is 1.663 and no(ω) is 1.648. We find that the positive birefringence Δn(0) is equal to 0.015 for w-ZnO.
The extinction co-efficient k(ω) indicates strongest absorption at the edge and above 8 eV (in the UV region). The line shape of k(ω) spectra in Figure 8(b) is having homogeneous nature with that of absorption spectra α(ω) in Figure 9(b) due to the absorptive nature of k(ω).
The calculated optical conductivity and absorption coefficient as a function of photon energy for pure w-ZnO with mBJLDA are shown in Figure 9(a), Figure 9(b). The expressions which are used for calculating the absorption co-efficient and optical conductivity from ɛ1(ω) and ɛ2(ω) are given in Equations (10) and (11).


Optical conductivity starts at 2.68 eV in both σ(ω)xx and σ(ω)zz spectra, which confirms that ZnO is a semiconductor. The highest optical peak is obtained at 11.7 eV in σ(ω)xx and at 13.2 eV in σ(ω)zz. The line shape of σ(ω)xx and σ(ω)zz are similar as ɛ2(ω) spectra. Absorption co-efficient is another important factor to evaluate the optical properties ofa material. The peaks and valleys in the absorption curve are related to the possible transition between states in the energy bands. The absorption spectra in Figure 9(b) reveal that w-ZnO is sensitive in the ultraviolet region.
The calculated real and imaginary parts of optical conductivity as a function of photon energy for pure w-ZnO with mBJLDA are shown in Figure 10(a), Figure 10(b). Real part of the optical conductivity Re σ(ω) is related to the frequency dependent dielectric function ɛ2(ω) in all frequencies. The peaks in Re σ(ω) are mainly from the interband transitions between the occupied and unoccupied states.
4. Conclusion
We have analysed the structural, electronic and optical properties of wurtzite ZnO using Full Potential Linearized Augmented Plane Wave (FP-LAPW) method. Exchange and correlation effects are treated by PBE- GGA and mBJLDA potentials. The structural parameters show good agreement with experimental values. The
Figure 8. (a) Calculated refractive index n(ω), and (b) extinction co-efficient κ(ω) as a function of photon energy for pure ZnO with mBJLDA.
band structure calculations are done using both the exchange correlation potentials. Since mBJLDA gives better band gap than PBE-GGA, further studies are carried out with the former potential. Total and partial densities of states of ZnO are also performed to understand the relative energetic positions of electrons and to know about the hybridization and nature of bonding. From the investigation of electronic charge density, it is found that ZnO has iono-covalent bonding nature. The optical properties, such as real and imaginary parts of dielectric function, reflectivity R(ω), refractive index n(ω), extinction co-efficient k(ω), absorption co-efficient α(ω), electron energy loss function L(ω) and optical conductivity σ(ω) are calculated. Our optical properties reasonably agree with other reported experimental and theoretical results.
Acknowledgements
One of the authors (S.P) acknowledges the financial support from Department of Science and Technology-
Figure 9. (a) Calculated optical conductivity σ(ω) and (b) absorption coefficient α(ω) as a function of photon energy for pure ZnO with mBJLDA.
Figure 10. (a) Calculated real and (b) imaginary part of optical conductivity as a function of photon energy for pure ZnO with mBJLDA.
Promotion of University Research and Scientific Excellence-phase II Fellowship. Mr. T. Samuel, application programmer of the Department of Theoretical Physics is acknowledged for his timely support during this work.
Cite this paper
Rita John,S. Padmavathi, (2016) Ab Initio Calculations on Structural, Electronic and Optical Properties of ZnO in Wurtzite Phase. Crystal Structure Theory and Applications,05,24-41. doi: 10.4236/csta.2016.52003
References
- 1. Serrano, J., Romero, A.H., Manjon, F.J., Lauck, R., Cardona, M. and Rubio, A. (2004) Pressure Dependence of the Lattice Dynamics of ZnO: An Ab Initio Approach. Physical Review B, 69, Article ID: 094306.
- 2. Hamdani, F., Botchkarev, A., Kim, W., Morkoc, H., Yeadow, M., Gibson, J.M., Tsen, S.C.Y., Smith, D.J., Evans, K., Litton, C.W., Michel, W.C. and Hemenger, P. (1997) Optical Properties of GaN Grown on ZnO by Reactive Molecular Beam Epitaxy. Applied Physics Letters, 70, 467.
http://dx.doi.org/10.1063/1.118183 - 3. Reynolds, D.C. and Collins, T.C. (1969) Excited Terminal States of a Bound Exciton-Donor Complex in ZnO. Physical Review, 185, 1099-1103.
http://dx.doi.org/10.1103/PhysRev.185.1099 - 4. Park, Y.S., Litton, C.W., Collins, T.C. and Reynolds, D.C. (1965) Exciton Spectrum of ZnO. Physical Review, 143, 512-519.
http://dx.doi.org/10.1103/PhysRev.143.512 - 5. Thomas, D.G. (1960) The Exciton Spectrum of Zinc Oxide. Journal of Physics and Chemistry of Solids, 15, 86-96.
http://dx.doi.org/10.1016/0022-3697(60)90104-9 - 6. Weiher, R.L. (1966) Optical Properties of Free Electrons in ZnO. Physical Review, 152, 736-739.
http://dx.doi.org/10.1103/PhysRev.152.736 - 7. Baer, W.S. (1967) Faraday Rotation in ZnO: Determination of Electron Effective Mass. Physical Review, 154, 785-789.
http://dx.doi.org/10.1103/physrev.154.785 - 8. Liang, W.Y. and Yoffe, A.D. (1968) Transmission Spectra of ZnO Single Crystals. Physical Review Letters, 20, 59-62.
http://dx.doi.org/10.1103/PhysRevLett.20.59 - 9. Freeouf, J.L. (1973) Far-Ultraviolet Reflectance of II-VI Compounds and Correlation with the Penn-Phillips Gap. Physical Review B, 7, 3810-3830.
http://dx.doi.org/10.1103/PhysRevB.7.3810 - 10. Schirmer, O.F. and Zwingel, D. (1970) The Yellow Luminescence of Zinc Oxide. Solid State Communications, 8, 1559-1563.
http://dx.doi.org/10.1016/0038-1098(70)90608-3 - 11. Hopfield, J.J. and Thomas, D.G. (1965) Polariton Absorption Lines. Physical Review Letters, 15, 22-25.
http://dx.doi.org/10.1103/PhysRevLett.15.22 - 12. Stephens, R.E. and Malitson, I.H. (1952) Index of Refraction of Magnesium Oxide. Journal of Research of the National Bureau of Standards, 49, 249-252.
http://dx.doi.org/10.6028/jres.049.025 - 13. De la Olvera, M.L. and Asomoza, R. (1997) SnO2 and SnO2: Pt Thin Films Used as Gas Sensors. Sensors and Actuators B, 45, 49-53.
http://dx.doi.org/10.1016/S0925-4005(97)00269-4 - 14. Gorla, C.R., Emanetoglu, N.W., Liang, S., Mayo, W.E., Lu, Y., Wraback, M. and Shen, H.J. (1999) Structural, Optical and Surface Acoustic Wave Properties of Epitaxial ZnO Films Grown on (011ˉ2) Sapphire by Metalorganic Chemical Vapour Deposition. Journal of Applied Physics, 85, 2595-2602.
http://dx.doi.org/10.1063/1.369577 - 15. Nomura, K., Ohta, H., Ueda, K., Kamiya, T., Hirano, M. and Hosono, H. (2003) Thin-Film Transistor Fabricated in Single-Crystalline Transparent Oxide Semiconductor. Science, 300, 1269-1272.
http://dx.doi.org/10.1126/science.1083212 - 16. Huang, M.H., Mao, S., Feick, H., Yan, H., Wu, Y., Kind, H., Weber, E., Russo, R. and Yang, P. (2001) Room-Temperature Ultraviolet Nanowire Nanolasers. Science, 292, 1897-1899.
http://dx.doi.org/10.1126/science.1060367 - 17. Lee, C.T., Su, Y.K. and Wang, H.M. (1987) Effect of R.F. Sputtering Parameters on ZnO Films Deposited onto GaAs Substrates. Thin Solid Films, 150, 283-289.
http://dx.doi.org/10.1016/0040-6090(87)90101-5 - 18. Rodnyi, P.A. and Khodyuk, I.V. (2011) Optical and Luminescence Properties of Zinc Oxide (Review). Optics and Spectroscopy, 111, 776-785.
http://dx.doi.org/10.1134/S0030400X11120216 - 19. Schleife, A., Rödl, C., Fuchs, F., Furthmüller, J. and Bechstedt, F. (2009) Optical and Energy-Loss Spectra of MgO, ZnO, and CdO from ab Initio Many-Body Calculations. Physical Review B, 80, Article ID: 035112.
- 20. Kong, F.J. and Jiang, G. (2009) Nonlinear Optical Response of Wurtzite ZnO from First Principles. Physica B: Condensed Matter, 404, 2340-2344.
http://dx.doi.org/10.1016/j.physb.2009.04.041 - 21. Smith, N.V. (1971) Photoelectron Energy Spectra and the Band Structure of the Noble Metals. Physical Review B, 3, 1862-1878.
http://dx.doi.org/10.1103/PhysRevB.3.1862 - 22. Sun, J., Wang, H.-T., He, J.L. and Tian, Y.J. (2005) Ab Initio Investigations of Optical Properties of the High-Pressure Phases of ZnO. Physical Review B, 71, Article ID: 125132(1-5).
- 23. Zhao, L., Lu, P.-F., Yu, Z.-Y., Liu, Y.-M., Wang, D.-L. and Ye, H. (2010) First-Principles Study of Electronic and Optical Properties in Wurtzite Zn1–xCuxO. Chinese Physics B, 19, Article ID: 056104.
- 24. Wooten, F. (1972) Optical Properties of Solids. Academic Press, New York.
- 25. Blaha, P. Schwarz, K. Madsen, G.K.H., Kvasnicka, D. and Luitz, J. (2001) WIEN2k: An Augmented Plane Wave plus Local Orbitals Program for Calculating Crystal Properties. Technische Universität, Wien, Austria.
- 26. Hohenberg, P. and Kohn, W. (1964) Inhomogeneous Electron Gas. Physical Review, 136, 864-871.
http://dx.doi.org/10.1103/PhysRev.136.B864 - 27. Becke, A.D. and Johnson, E.R. (2006) A Simple Effective Potential for Exchange. The Journal of Chemical Physics, 124, Article ID: 221101.
- 28. Tran, F. and Blaha, P. (2009) Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential. Physical Review Letters, 102, Article ID: 226401.
- 29. Perdew, J.P., Burke, S. and Ernzerhof, M. (1996) Generalized Gradient Approximation Made Simple. Physical Review Letters, 77, 3865-3868.
http://dx.doi.org/10.1103/PhysRevLett.77.3865 - 30. Khan, I., Ahmad, I., Rahnamaye Aliabad, H.A. and Maqbool, M. (2012) Effect of Phase Transition on the Optoelectronic Properties of Zn1–xMgxS. Journal of Applied Physics, 112, Article ID: 073104.
- 31. Ali, Z., Ali, S., Ahmad, I., Khan, I. and Rahnamaye Aliabad, H.A. (2013) Structural and Optoelectronic Properties of the Zinc Titanate Perovskite and Spinel by Modified Becke-Johnson Potential. Physica B: Condensed Matter, 420, 54-57.
http://dx.doi.org/10.1016/j.physb.2013.03.042 - 32. Birch, F. (1947) Finite Elastic Strain of Cubic Crystal. Physical Review, 71, 809-824.
http://dx.doi.org/10.1103/PhysRev.71.809 - 33. Murnaghan, F.D. (1944) The Compressibility of Media under Extreme Pressures. Proceedings of the National Academy of Sciences of the United States of America, 30, 244-247.
http://dx.doi.org/10.1073/pnas.30.9.244 - 34. Karzel, H., Potzel, W., Kufferlein, M., Schiessl, W., Steiner, M., Hiller, U., Kalvius, G.M., Mitchell, D.W., Das, T.P., Blaha, P., Schwarz, K. and Pasternak, M.P. (1996) Lattice Dynamics and Hyperfine Interactions in ZnO and ZnSe at High External Pressures. Physical Review B, 53, 11425-11438.
http://dx.doi.org/10.1103/PhysRevB.53.11425 - 35. Catti, M., Noel, Y. and Dovesi, R. (2003) Full Piezoelectric Tensors of Wurtzite and Zinc Blende ZnO and ZnS by First-Principles Calculations. Journal of Physics and Chemistry of Solids, 64, 2183-2190.
http://dx.doi.org/10.1016/S0022-3697(03)00219-1 - 36. Shein, R., Kioeko, V.S., Makurin, Y.N., Gorbunova, M.A. and Ivanovskioe, A.L. (2007) Elastic Parameters of Single-Crystal and Polycrystalline Wurtzite-Like Oxides BeO and ZnO: Ab Initio Calculations. Physics of the Solid State, 49, 1067-1073.
http://dx.doi.org/10.1134/S106378340706008X - 37. Charifi, Z., Baaziz, H. and Reshak, A.H. (2007) Ab-Initio Investigation of Structural, Electronic and Optical Properties for Three Phases of ZnO Compound. Physica Status Solidi (b), 244, 3154-3167.
http://dx.doi.org/10.1002/pssb.200642471 - 38. Schleife, A., Fuchs, F., Furthmüller, J. and Bechstedt, F. (2006) First Principles Study of Ground and Excited State Properties of MgO, ZnO, and CdO Polymorphs. Physical Review B, 73, Article ID: 245212.
http://dx.doi.org/10.1103/PhysRevB.73.245212 - 39. Okoye, C.M.I. (2003) Theoretical Study of the Electronic Structure, Chemical Bonding and Optical Properties of KNbO3 in the Paraelectric Cubic Phase. Journal of Physics: Condensed Matter, 15, 5945-5958.
http://dx.doi.org/10.1088/0953-8984/15/35/304 - 40. Fox, M. (2001) Optical Properties of Solids. Oxford University Press, New York.
- 41. Ahuja, R., Eriksson, O., Johansson, B., Auluck, S. and Wills, J.M. (1996) Electronic and Optical Properties of Red HgI2. Physical Review B, 54, 10419-10424.
http://dx.doi.org/10.1103/PhysRevB.54.10419 - 42. Penn, D.R. (1962) Wave Number Dependent Dielectrics Function of Semiconductors. Physical Review, 128, 2093-2097.
http://dx.doi.org/10.1103/PhysRev.128.2093 - 43. Hengehold, R.L., Almassy, R.J. and Pedrotti, F.L. (1970) Electron Energy-Loss and Ultraviolet-Reflectivity Spectra of ZnO. Physical Review B, 1, 4784-4791.
http://dx.doi.org/10.1103/PhysRevB.1.4784
NOTES
*Corresponding author.



























