Crystal Structure Theory and Applications
Vol.3 No.2(2014), Article
ID:47510,8
pages
DOI:10.4236/csta.2014.32006
1-D Paracrystalline Model to Simulate a Bragg Reflection: Computation of Crystallite Size and Lattice Strain
M. B. Nanda Prakash1, G. Thejas Urs1, H. T. Ananda2, R. Somashekar1*
1Department of Studies in Physics, University of Mysore, Mysore, India
2Department of Physics, Government College (Autonomus), Mandya, India
Email: *rs@physics.uni-mysore.ac.in
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 April 2014; revised 28 May 2014; accepted 27 June 2014
ABSTRACT
A simple and elegant method to simulate single order reflection profile based on 1-D paracrystalline model has been proposed here. For variety of polymer films this approach has been applied to compute microcrystalline parameters like crystallite size and lattice strain. Other metallic oxide compounds are also analysed using this approach. Employing this model, X-ray diffraction patterns from various polymer samples have been analysed and corresponding microstructure parameters have been reported in this article.
Keywords:X-Ray Diffraction, Paracrystal, Simulation

1. Introduction
Broadening of Bragg reflections in polymer/metal oxide samples has drawn attention of many crystallographers for developing a technique to quantify the patterns [1] -[13] . A modified Williamson-Halland Warren-Averbach procedure was given by [14] . International union of crystallography has brought out a monograph on this subject in 1999 for the benefit of investigators working on materials science [15] . For ball milled Ni X-ray powder samples, a whole powder pattern modelling based on modelling of diffraction pattern was reported [8] . Later on several investigators also explored the possibility of computing crystallite size and lattice strain from single line profile analysis X-ray data [16] . This was of main interest for investigators carrying out research work on natural and man-made polymers to bring out structure-property relation in these materials [17] . Employing various distribution functions and Hosemann’s paracrystalline model, single line profile analysis was also proposed during this period [18] . In fact this method was used during the participation of Round Robin analysis of standard samples [19] . A simple program for extracting microstructure information from X-ray diffraction patterns has been reported [20] . The accurate powder diffraction peak profile by numerical procedure has been reported [21] . An elegant method of computation of common volume fraction of any type of polyhedra has been reported [22] . In this article it is very clear that the crystallite size is different along different Bragg angles and assumption of symmetric crystallite size as done in various other methods is not appropriate. There is a continued interest in this endeavour, as many have expressed the inability of obtaining a reliable set of parameters. This article is in this direction of suggesting an improved method based on Hosemann’s 1-dimensional paracrystalline model which can be used to compute microcrystalline parameters for both polymer and metal oxide materials. If the periodicity along one direction, with an assumption that the lateral size is infinitely large as compared to the longitudinal periodicity, it can be treated as 1-dimensional problem even though it is, physically, a 3D problem. The treatment of 1-D problem is rigorous, analytical and has been derived more than 80 years ago. Here we have used the same result with slight modifications.
2. Theory
Let us consider, at random, a set of rods of length “d” such that this length is distributed around a mean value “x”. Here let us assume that the distance probability is a Gaussianin shape and it is identified by H1(x). The average length is given by
 (1)
(1)
Using H1(x) we can calculate the probability distribution of length vectors by the propagation of errors. The position of second Gaussian is
 (2)
(2)
where “*” represents convolution process. The average length of second vector is given the Equation (1) with H2(x). The probability distribution thus produced forms a one dimensional lattice with an atom/molecule at lattice edge. The Gaussian function is normalised so that all the peaks have an area of 1. We can continue this to find nth lattice point. This is done as follows:
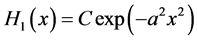 (3)
(3)
where ,
, 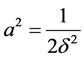 and δ is the lattice strain. Convolution of this function at x1 is given by
and δ is the lattice strain. Convolution of this function at x1 is given by
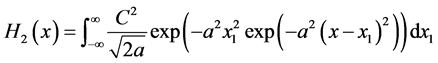 (4)
(4)
With a substitution  and using
and using 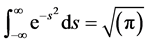 we find
we find
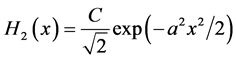 (5)
(5)
Extending this to the nth Gaussian we get
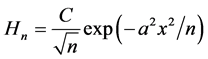 (6)
(6)
Taking the Fourier cosine transformation, we have
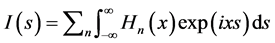 (7)
(7)
the intensity profile due to convolution of “n” Gaussians. Figure 1(a) and Figure 1(b), and Figure 2(a) and Figure 2(b) show the simulation of convoluted Gaussians and their intensity profile for.
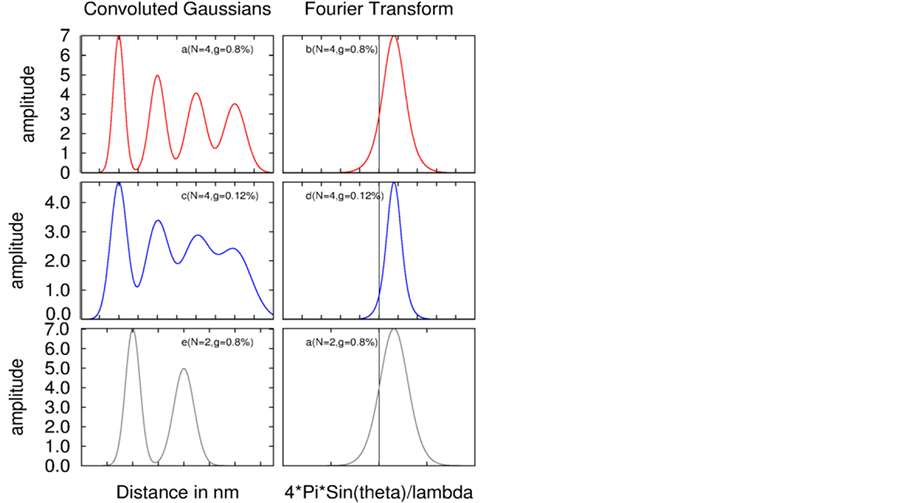
Figure 1. Convolution of Gaussians and their Fourier transform: N (number of convoluted Gaussians) and g is percentage of lattice distortion. First Gaussian Peak is located at 0.4 nm and corresponding peak position in Fourier transformed is located at 15.70.
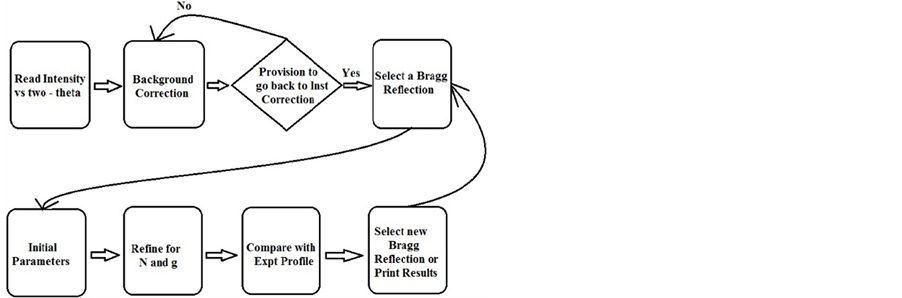
Figure 2. Flowchart for the computation of microstructural parameters and simulation of the experiment pattern.
Solution to the Equation (7) is
 (8)
(8)
where
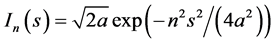 (9)
(9)
with 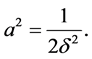
Crystallite Size Probability Distribution
The crystallite size distribution at t shifted by a distance equal to dth position (last Gaussian), we have
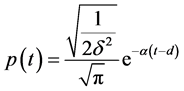 (10)
(10)
where 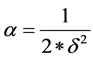 is the width of the distribution. Thus the contribution of the shape function at this point is
is the width of the distribution. Thus the contribution of the shape function at this point is
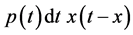 (11)
(11)
Here (t − x) is the shape function. Thus the resulting shape function will be
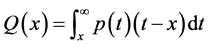 (12)
(12)
We get
 (13)
(13)
The Fourier transform of this equation is given by
 (14)
(14)
Substituting for Q(x) we get
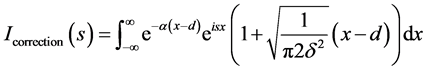 (15)
(15)
Consider the first term. Since p(t) is +ve, we take x → |x| and then carry out the integration by breaking it into two terms.
 (16)
(16)
The first and second integrations give
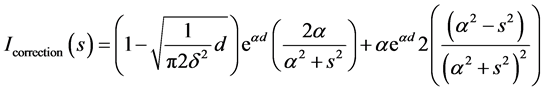 (17)
(17)
With this incorporation of correction we have an expression for the intensity as
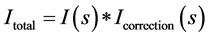 (18)
(18)
3. Application of the Procedure
For computation of crystallite size and strain from X-ray diffraction pattern, it is important to have good experimental data. We have used eight polymer samples wherein reasonably good X-ray data is available. The samples are two cotton fibers (SAHANA, JAYADHAR), two silk fibers (TASSAR, MUGA) and two polymers (HPMC, PVA). The flowchart for the computation of crystallite size and strain is given in Figure 2. The results are given in Table1 To begin with X-ray powder data is corrected for instrumental broadening using Stokes method [23] . Then onwards, X-ray data as input to the program, starts with number of profiles. Beginning, peak position and end of each profiles are given as input using GUI method. Program searches for a good set of microstructural parameters including the width of asymmetric exponential column length distribution till one obtains a reasonable goodness standard deviation between simulated and experimental whole powder pattern recorded from the sample. This is checked visually also. An option is provided in the program for a slight variation in the parameter for a possible good fitting between simulated and experimental whole powder pattern data. The routine also give in the output appropriate standard deviation in these microstructural parameters. Figure 3 and Figure 4 show the goodness of the whole powder patter fitting technique suggested here.
Table 1. Microstructural parameters for natural and man-made polymers using the present and earlier methods.
(a)[24] [25] ; (b)[26] [27] ; (c)[29] [30] ; (d)[28] [29] ; (e)[31] ; (f)[31] [32] .

Figure 3. Comparison of experimental and simulated whole powder pattern X-ray profiles. Right side gives column length exponential distribution.
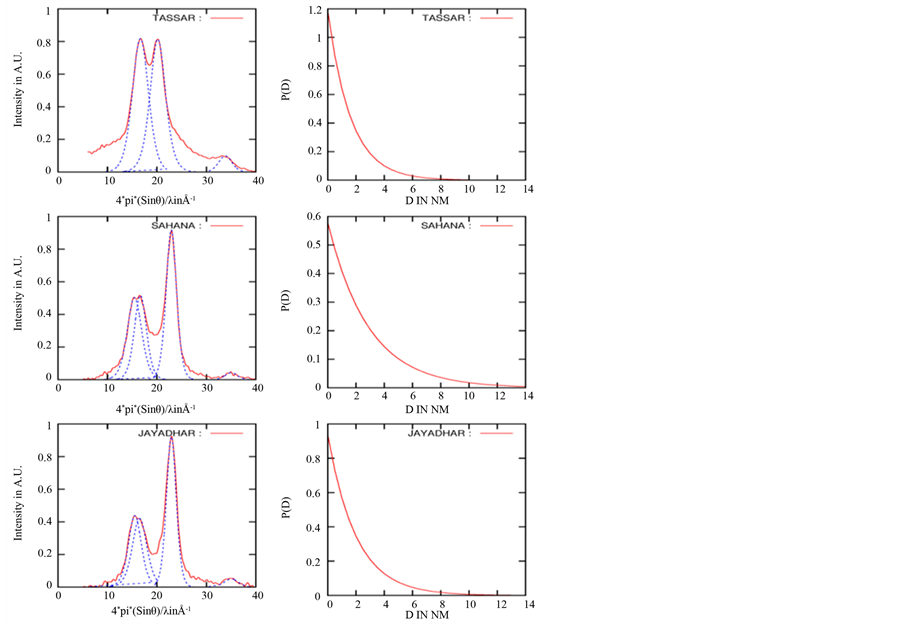
Figure 4. Comparison of experimental and simulated whole powder pattern X-ray profiles. Right side gives column length exponential distribution.
4. Results and Discussion
Samples chosen here represents reasonably amorphous in nature, in a sense that a well defined delta-type Bragg reflections are rarely observed. Scherrer and Williamson-Hall methods relay on 1) instrumental broadening correction, 2) background correction and 3) accuracy of measuring FWHM using peak fit and peak separation procedures. Multiple and single order Fourier methods by Warren and others do relay on initial Fourier coefficients. In all these methods, our experience suggest that while refining the parameters against the profile and hence the whole powder pattern, the program selectively choose to give more weightage to the crystalline parameter than lattice strain parameter leading to either over or under estimation of crystallite size. Normally in polymers we have a situation where in a few unit cells contributes for a Bragg reflection. Under these circumstances we look for a method which can compute microstructural parameters with reasonable accuracy in a straight forward manner. In this direction, present method is quite useful. As mentioned in the flow chart, an approximate crystallite size is estimated using Nandi et al.’s initial slope method for a selected profile after all the corrections. This is done using Graphic User Interface technique wherein the beginning, peak and end of the profile is selected graphically in the program. Then the parameters like background, size and strain are varied continuously such that the final parameters are used to simulate the profile. This process is continued for all the available profiles. At the end of the day, all the profile parameters are used to compute the whole powder pattern to an accuracy which is always less than 5 percent between the simulated and experimental profiles, which is also verified visually using the graphics user interface in the program. The results are in broad agreement with single order Fourier method based on Warrens approach used earlier.
5. Conclusion
Essentially, crystallite size is the region between defects. Associated with this, there are non-uniform strains leading to shifts of atoms/molecules from their ideal positions. These two together along with other extended defects lead to peak broadening. Absolute accuracy of these results is always a problem. The restrictions are less stringent if one seeks results in a semi-quantitative manner. Here in a straight forward method, using exponential column length distribution, crystallite size is computed by a visual inspection of the profile and also the whole pattern. It is observed that it is difficult to extract accurate parameters from Rietveld analysis when the peak shape is mixed Gaussian-Lorentzian. Here the accuracy can be improved by the goodness off it in terms of simplified peak shape.
Acknowledgements
Authors acknowledge UPE and CPEPA grants from UGC, NewDelhi, India.
Program is freely available at the site faculty.physics.uni-mysore.ac.in/rs.
References
- Zernike, F. and Prins, J.A. (1927) Die Beugung von Rontgenstrahlen in Flussigkeiten als Effekt der Molekulanordnung. Zeitschrift fur Physik, 41, 184-194. http://dx.doi.org/10.1007/BF01391926
- Warren, B.E. (1969) X-Ray Diffraction. Addison-Wesley, Reading.
- Hosemann, R. and Bagchi, S.N. (1962) Direct Analysis of Diffraction by Matter. North-Holland, Amsterdam.
- Hall, I.H. and Somashekar, R. (1991) The Determination of Crystal Size and Disorder from the X-Ray Diffraction Photograph of Polymer Fibres. 2. Modelling Intensity Profiles. Journal of Applied Crystallography, 24, 1051.http://dx.doi.org/10.1107/S0021889891007707
- Balzar, D. (1993) X-Ray Diffraction Line Broadening: Modeling and Applications to High-Tc Superconductors. Journal of Research of the National Institute of Standards and Technology, 98, 321. http://dx.doi.org/10.6028/jres.098.026
- Delhez, R., de Keijser, Th.H., Langford, J.L., Louer, D., Mittemeijer, E.J. and Sonneveld, E.J. (1993)
- Langford, J.I. and Lour, D. (1982) Diffraction Line Profiles and Scherrer Constants for Materials with Cylindrical Crystallites. Journal of Applied Crystallography, 15, 20-26. http://dx.doi.org/10.1107/S0021889882011297
- Scardi, P. and Leoni, M. (2002) Whole Powder Pattern Modeling. Acta Crystallographica Section A. Foundations of Crystallography, 58, 190-200. http://dx.doi.org/10.1107/S0108767301021298
- Nandi, R.K., Kuo, H.K., Schlosberg, W., Wissler, G., Cohen, J.B. and Crist Jr., B. (1984) Single-Peak Methods for Fourier Analysis of Peak Shapes. Journal of Applied Crystallography, 17, 22-26. http://dx.doi.org/10.1107/S0021889878012662
- Klug, H.P. and Alexander, L.E. (1974) X-Ray Diffraction Procedures for Polycrystalline and Amorphous Materials. 2nd Edition, Wiley, New York.
- Kuzel Jr., R. and Klimanek, P. (1989) X-Ray Diffraction Line Broadening Due to Dislocations in Non-Cubic Crystalline Materials. III. Experimental Results for Plastically Deformed Zirconium. Journal of Applied Crystallography, 22, 299-307. http://dx.doi.org/10.1107/S0021889889001585
- Rietveld, H.M. (1969) A Profile Refinement Method for Nuclear and Magnetic Structures. Journal of Applied Crystallography, 2, 65-71. http://dx.doi.org/10.1107/S0021889869006558
- Young, R.A. (1995) The Rietveld Method. Oxford University Press, Oxford, 132-166.
- Ungar, T., Gubicza, J., Ribarik, G. and Borbely, A. (2001) Crystallite Size Distribution and Dislocation Structure Determined by Diffraction Profile Analysis: Principles and Practical Application to Cubic and Hexagonal Crystals. Journal of Applied Crystallography, 34, 298-310. http://dx.doi.org/10.1107/S0021889801003715
- Snyder, R.J., Fiala, J. and Bunge, H.J. (1999) Defect and Microstructure Analysis by Diffraction. Oxford University Press, Oxford.
- Somashekar, R., Hall, I.H. and Carr, P.D. (1989) The Determination of Crystal Size and Disorder from X-Ray Diffraction Photographs of Polymer Fibres. 1. The Accuracy of Determination of Fourier Coefficients of the Intensity Profile of a Reflection. Journal of Applied Crystallography, 22, 363-371. http://dx.doi.org/10.1107/S0021889889004085
- Lee, K.G., Barton, R. and Schultz, J.M. (1995) Structure and Property Development in Poly(P-Phenylene Terephthalamide) during Heat Treatment under Tension. Journal of Polymer Science Part B: Polymer Physics, 33, 1-14.http://dx.doi.org/10.1002/polb.1995.090330101
- Somashekar, R. and Somashekarappa, H. (1997) X-Ray Diffraction-Line Broadening Analysis: Paracrystalline Method. Journal of Applied Crystallography, 30, 147-152. http://dx.doi.org/10.1107/S0021889896010023
- Balzar, D., Audebrand, N., Daymond, M.R., Fitch, A., Hewat, A., Langford, J.I., Le Bail, A., Lour, D., Masson, O., McCowan, C.N., Popa, N.C., Stephens, P.W. and Toby, B.H. (2004) Journal of Applied Crystallography, 37, 911-924. http://dx.doi.org/10.1107/S0021889804022551
- Skoko, Z., Popovic, J., Dekanic, K., Kolbas, V. and Popovi, S. (2012) XBroad: Program for Extracting Basic Microstructure Information from X-Ray Diffraction Patterns in Few Clicks. Journal of Applied Crystallography, 45, 584-597. http://dx.doi.org/10.1107/S0021889812014859
- Beyerlien, K.R., Snyder, R.L. and Scardi, P. (2011) Powder Diffraction Line Profiles from the Size and Shape of Nanocrystallites. Journal of Applied Crystallography, 44, 945-953. http://dx.doi.org/10.1107/S0021889811030743
- Leonardi, A., Leoni, M., Siboni, S. and Scardi, P. (2012) Common Volume Functions and Diffraction Line Profiles of Polyhedral Domains. Journal of Applied Crystallography, 45, 1162-1172. http://dx.doi.org/10.1107/S0021889812039283
- Stokes, A.R. (1948) A Numerical Fourier-Analysis Method for the Correction of Widths and Shapes of Lines on X-Ray Powder Photographs. Proceedings of the Physical Society, 61, 382-391. http://dx.doi.org/10.1088/0959-5309/61/4/311
- Bhajantria, R.F., Ravindrachary, V., Harisha, A., Crasta, V., Nayak, S.P. and Poojary, B. (2006) Microstructural Studies on BaCl2 Doped Poly(Vinyl Alcohol). Polymer, 47, 3591-3598. http://dx.doi.org/10.1016/j.polymer.2006.03.054
- Lakshmeesha Rao, B., Mahadevaiah, O., Sangappa, Y., Asha, S. and Somashekar, R. (2012) Microstructural Parameters in Electron Irradiated PVA Films by Wide Angle X-Ray Scattering Studies (WAXS). Advanced Materials Research, 585, 532-536. http://dx.doi.org/10.4028/www.scientific.net/AMR.585.532
- Divakara, S., Siddaraju, G.N. and Somashekar, R. (2010) Comparative Study of Natural and Man-Made Polymers Using Whole Powder Pattern Fitting Technique. Fibres and Polymers, 11, 861-868. http://dx.doi.org/10.1007/s12221-010-0861-7
- Sangappa, Demappa, T., Mahadevaiah, Ganesh, S., Divakara, S. and Somashekar, R. (2008) Microstructural Parameters in Electron-Irradiated Hydroxypropyl Methylcellulose Films Using X-Ray Line Profile Analysis. Journal of Applied Polymer Science, 109, 3983-3990. http://dx.doi.org/10.1002/app.28495
- Divakara, S., Madhu, S. and Somashekar, R. (2009) Stacking Faults and Microstructural Parameters in Non-Mulberry Silk Fibres. Pramana, 73, 927-938. http://dx.doi.org/10.1007/s12043-009-0159-8
- Divakara, S., Somashekar, R. and Roy, S. (2009) Correlation between Microstructure and Microrheological Parameters of Various Silk Fibres. Indian Journal of Fibre and Textile Research, 34, 168-174.
- Reddy, T., Roy, S., Prakash, Y., Somashekarappa, H., Ramesh, K., Divakara, S. and Somashekar, R. (2011) Stress-Strain Curves and Corresponding Structural Parameters in Mulberry and Non-Mulberry Silk Fibers. Fibers and Polymers, 12, 499-505. http://dx.doi.org/10.1007/s12221-011-0499-0
- Niranjana, A.R., Divakara, S. and Somashekar, R. (2011) Characterization of Field Grown Cotton Fibres Using Whole Powder Pattern Fitting Method. Indian Journal of Fibre and Textile Research, 36, 9-17.
- Abhishek, S., Samir, O.M., Annadurai, V., Gopalkrishne Urs, R., Mahesh, S.S. and Somashekar, R. (2005) Role of Micro-Crystalline Parameters in the Physical Properties of Cotton Fibers. European Polymer Journal, 41, 2916-2922. http://dx.doi.org/10.1016/j.eurpolymj.2005.06.005
NOTES

*Corresponding author.


