Crystal Structure Theory and Applications
Vol.1 No.2(2012), Article ID:23031,4 pages DOI:10.4236/csta.2012.12003
An Investigation of PLD-Deposited Barium Strontium Titanate (BaxSr1−xTiO3) Thin Film Optical Properties
Department of Electrical Engineering, Northern Illinois University, DeKalb, USA
Email: *mkocanda1@niu.edu
Received July 9, 2012; revised August 12, 2012; accepted August 20, 2012
Keywords: Barium Strontium Titanate; Optical Bandgap; Optical Conductivity; Pulsed Laser Deposition; Stoichiometry
ABSTRACT
Reflectance and transmittance parameters of pulsed laser deposited barium strontium titanate (BST) were investigated using spectrophotometric methods. Three stoichiometries consisting of BaxSr1−xTiO3 (x = 0.30, 0.40, 0.50) were deposited on glass substrates using oxygen partial pressures of 1.3 Pa ± 0.13 Pa at 500˚C. Subsequently, the measured optical parameters were employed to determine the refractive index (n), extinction coefficient (k), optical conductivity (σ), absorption coefficient (α) and optical bandgap (Eg) using swept spectra in the ultraviolet, visible and near-infrared range (200 nm - 1100 nm) as these have not been reported in the literature. The calculated parameters for Ba0.4Sr0.6TiO3 are reported in this experimental work. Minimal differences in the transmittance have been observed at the visible band edges when comparing each stoichiometry. Sharp cutoffs were observed at the bands edges and strong absorbance in the 200 nm - 300 nm band as attributed to the crystal structure based upon the oxygen partial pressure during the deposition process.
1. Introduction
High-k materials have been of interest in shrinking the transistor geometries contained in microcontrollers, microprocessors and related microelectronic devices. Moreover, high-k materials have advanced the design of capacitors where shrinking geometries again have been of interest. Recent work has also shown that high-k perovskite structures are suitable sensor substrates to bind biological compounds to determine genetic matching [1-4]. The optical properties of barium strontium titanate (BST) have not been widely investigated, however. The success of state-of-the-art optoelectronic devices has been dependent upon recent improvements in material quality and process techniques. The successful development of these devices has been dependent upon knowledge of band gap measurements and related electrical parameters. Optical properties of thin-film structure as applied to semiconductor substrates have been marginally investigated however, and merit further work.
Optical spectroscopy techniques have been generally employed by analytical chemists to characterize absorbance, transmittance, and reflectance of liquid-phase and solid-phase materials such as pigments, organic and inorganic coatings, optical films, and optical filters. Spectroscopy requires measurements performed within a segment of the spectrum of interest to characterize the desired optical or electronic properties. From the basic spectrometric measurements, related optical parameters such as refractive indices or absorption coefficients may be derived.
Variation of absorption coefficients with respect to photon energies (hν) provides information about the band gaps of the material. Direct bandgap ferroelectric materials such as barium strontium titanate (Ba1−xSrxTiO3) appear to have desirable properties based upon these measurements, also owing to their large electrical field-dependent dielectric constant and fast response. BST contains a face centered cubic (FCC) derivative structure of the form ABO in which the larger A cation and oxygen together form an FCC lattice while the smaller B cation occupies the octahedral interstitial sites in the FCC array [5]. Depending on the composition, BST thin films are stable and exhibit good crystalline structure, grain size, and excellent dielectric properties over a wide range of temperatures. BST thin films are relatively easy to fabricate using several techniques. The applied films usually exhibit uniform surface morphologies when deposited using pulsed laser deposition at high temperatures and small oxygen pressures. In this investigation, we have utilized three distinct cation stoichiometries—Ba0.3Sr0.7TiO3, Ba0.4Sr0.6TiO3 and Ba0.5Sr0.5TiO3 for experimental work. The optical parameter of Ba0.4Sr0.6TiO3 thin films has been subsequently calculated and reported using the measured transmittance and reflectance response in the 200 nm to 1100 nm range.
2. Experimental
High purity BST targets were prepared by the Northern Illinois Department of Physics. Components were prepared to provide the three desired stoichiometric ratios. The powders were mixed, pressed and sintered. X-ray diffraction analysis was performed to verify the stoichiometry and confirmed that the ratios were as expected. The targets were packaged and stored in nitrogen until required.
Glass microscope slides were selected as the substrates. The substrates were cleaned in a multi-step process. A mild soap solution was used as a degreasing step followed by rinsing in deionized water. A second cleaning cycle was performed using an acetone soak for five minutes and subjected to a rinse in isopropyl alcohol. The substrates were then rinsed in deionized water and air dried at 80˚C in a process oven.
The PLD technique was performed at Northern Illinois University’s Microelectronic Research and Development Laboratory (MRDL) using a 50 mJ KrF excimer laser. The process entailed deposition using one target per cycle, as the PLD system does not support multiple targets. Thus, the process required the removal and replacement of targets of each composition. The parameters used for the deposition process were consistent for each of the three stoichiometries. The chamber pressure was maintained at 1.3 × 10−4 Pa, the substrate temperature was maintained at 400˚C and the oxygen (O2) pressure was maintained at 1.3 Pa ± 0.13 Pa. The laser was pulsed at 10 Hz for 20,000 pulses, thus depositing a nominal 50 nm BST thin-film.
Optical analysis of the BST films employed a PerkinElmer Lambda 35 spectrophotometer with an integrating sphere. This instrument employs a dual-beam measurement method where a single light beam is split to provide a reference signal and a measurement beam that passes through the sample, compared and then normalized with respect to the reference signal over 200 nm - 1200 nm. The spectrometer was set with a suitable slit width of 1 nm in the measured spectral range.
3. Results and Discussion
Optical transmittance spectra of BST thin films closely follow a similar profile; the samples exhibit near-perfect levels of transmittance in the near-infrared (NIR) and visible regions (1100 - 400 nm) of the electromagnetic spectrum. The transmittance sharply decreases in the ultraviolet (UV) region of the spectrum (400 - 250 nm) and exhibits an increase with shorter wavelengths (200 - 250 nm), as shown in Figure 1. The range of the spectrophotometer is limited to this region only.
Optical transmittance spectra are employed to calculate the refractive index using the envelope method proposed by Swanepoel [6]. The refractive index (n) has been obtained using the following expressions;
 (1)
(1)
where
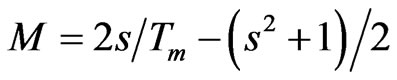 (2)
(2)
for all optically transparent regions, and
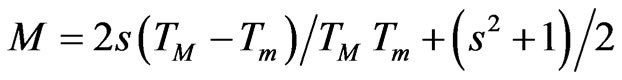 (3)
(3)
for weak and medium absorbance regions. TM and Tm are the values of maximum and minimum transmission at a specific wavelength. “s” is the refractive index of the substrate (glass). The refractive index of glass used in the experimental work is 1.517 for this spectral region. The refractive index can be estimated by extrapolating envelopes corresponding to TM and Tm using Swanepoel’s method [6]. As the thickness of film is uniform, interference gives rise to the spectrum as shown in Figure 1. These fringes can be used to calculate the refractive index (n) of the thin films using Equations (1)-(3). The refractive index corresponding to TM and Tm for the same wavelengths are calculated. The variation of refractive index with wavelength for Ba0.4Sr0.6TiO3 thin film is shown in Figure 2. The average refractive index for the Ba0.4Sr0.6TiO3 thin film was calculated to be 2.14. The reported value in literature for the refractive index of BST thin films is 2.25 for Ba0.5Sr0.5TiO3 at 410 nm [7].
The extinction coefficient defines several different measures of the absorption of light in a medium. By definition, the extinction coefficient is the imaginary part

Figure 1. Transmittance (%T) as a function of wavelength for BaxSr1−xTiO3 (x = 0.30, 0.40, 0.50) on glass substrates.

Figure 2. The calculated refractive index (n) as a function of wavelength for Ba0.4Sr0.6TiO3 deposited on glass substrates is shown using Swanepoel’s method.
of the complex index of refraction which also relates to light absorption. The extinction coefficient can be calculated by using the relation [8]
 (4)
(4)
where “α” is the absorption coefficient and is calculated from the relation [8].
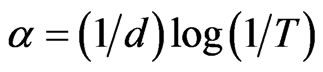 (5)
(5)
where d is the thickness of the film, and T is the transmittance value at a specific wavelength.
Figure 3 shows the variation of extinction coefficient with photon energy, where the wavelength has been converted to photon energy. The value of the extinction coefficient increases with an increase in energy of the incident beam for energies below 4.1 eV. It is observed that the extinction coefficient decreases with increase in the photon energy for energies greater than 4.1 eV. This may be due to the large absorption coefficient for higher energy values, as shown in Figure 4.
The absorption coefficient depends on the material and also on the wavelength of light absorbed. Semiconductor materials typically exhibit a sharp edge in their absorption coefficient; as light possessing energy below the band gap does not have sufficient energy to excite an electron into the conduction band from the valence band. Consequently this light is not absorbed and will be transmitted. Figure 4 exemplifies that for photons having energy above the bandgap, the absorption coefficient is not constant, but still depends strongly on wavelength.
The probability of absorbing a photon depends on the likelihood of having a photon and an electron interact in such a way as to move from one energy band to another. For photons possessing energy near the bandgap, the absorption is relatively low as only those electrons directly at the valence band edge can interact with the photon to cause absorption. Moreover, as the photon energy increases, these electrons close to that of the band gap can interact with the photon. Therefore, a larger number of electrons can interact with the photon and result in the photon being absorbed. Figure 5 shows the change of optical conductivity with the incident photon energy. The optical conductivity is determined using the relation [8].
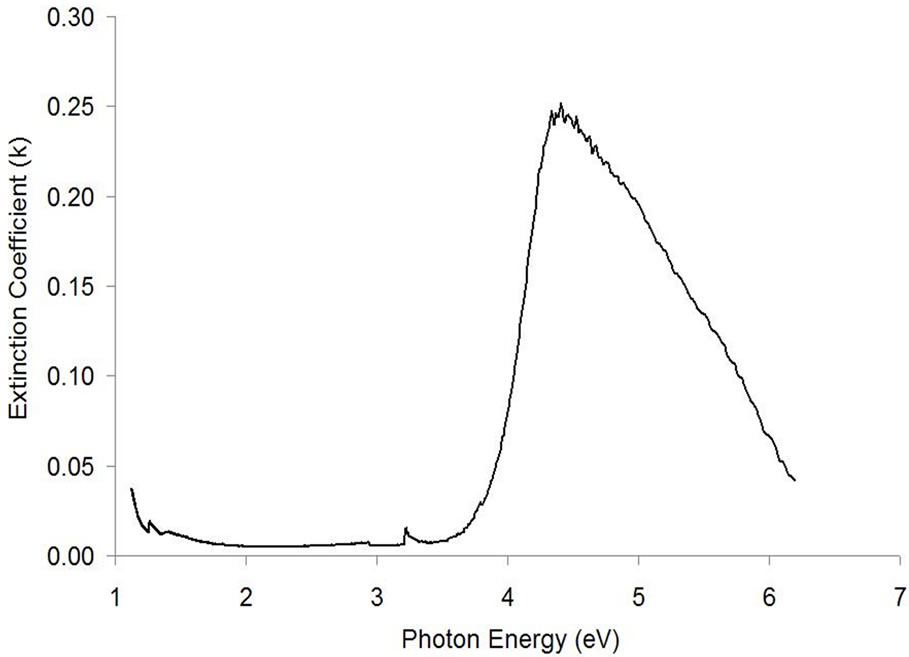
Figure 3. The extinction coefficient (k) as a function of photon energy for Ba0.4Sr0.6TiO3 as calculated using Equation (4).
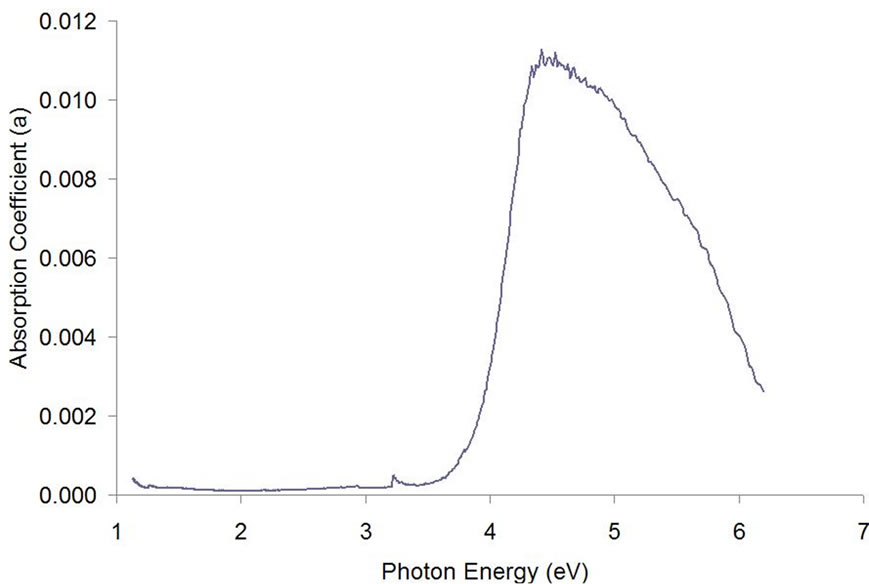
Figure 4. Absorption coefficient as a function of energy for Ba0.4Sr0.6TiO3 as calculated using Equation (5).
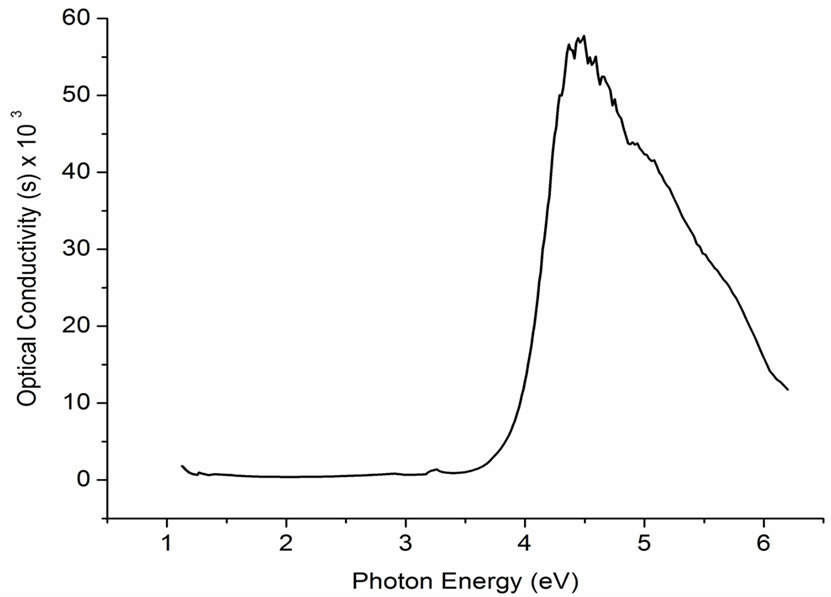
Figure 5. Optical conductivity (σ) as a function of energy for Ba0.4Sr0.6TiO3 as calculated using Equation (6).
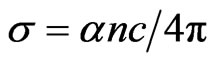 (6)
(6)
where “c” is the velocity of light, α is the absorption coefficient and n is the refractive index. The optical conductivity depends on the absorption coefficient and was found to increase sharply for energy values above 4.1 eV due to large absorption coefficient for these values.
The optical bandgap is found from the variation of the absorption coefficient with energy (hv), i.e., the energy corresponding to the wavelength for which is the absorption coefficient starts to increase [9]. The energy bandgap was found to be 3.35 eV, which is in close agreement with the literature values (3.4 - 3.6) for BST thin films [10]. Figure 6 shows the change in the absorption coefficients with respect to the wavelength of the incident beam.
4. Conclusion
Optical transmission measurements of PLD-applied BST using spectrophotometric methods appear to produce parametric results consistent with those reported in the literature. Using the Swanepoel method to calculate refractive index for Ba0.4Sr0.6TiO3 produces n = 1.97 at 400 nm. The optical parameters extinction coefficient, optical conductivity, absorption coefficient and optical band gap are calculated and coincide with literature values. BST thin films exhibit near perfect transmission in the Infrared (IR) and visible regions of the electromagnetic spectrum, with high absorbance in the Ultraviolet (UV) regions. Future work shall investigate the electrical turnability of BST in the optical region. This work merits further investigation as it may be possible to selectively control the optical properties of several BST stoichiometries under DC bias.

Figure 6. Absorption coefficient (α) as a function of wavelength for Ba0.4Sr0.6TiO3 as calculated using Equation (5).
5. Acknowledgements
This work was supported by the Department of Electrical Engineering and the College of Engineering and Engineering Technology at Northern Illinois University. The authors would like to thank Dean Promod Vohra for providing support to help in purchasing some of the measurement and testing equipment used in this study. The authors would like to acknowledge the help provided by the Department of Physics at Northern Illinois University in preparing the targets, especially Professors Bodgan Dabrowski, Clyde Kimball, and Omar Chmaissem. The authors would also like to thank Prof Michael Haji Sheikh of the department of Electrical Engineering for his help in material processing and measurements, and Mr. Gregg Westberg, the MRDL (Clean Room) manager, for training the students on the use of the laboratory equipment.
REFERENCES
- M. Kocanda and I. Abdel-Motaleb, “Design of a DNA Probe Using Barium Strontium Titanate,” Proceedings of International Conference on Solid-State and Integrated Circuit Technology, Beijing, 20-23 October 2008, pp. 2573-2576. doi:10.1109/ICSICT.2008.4735098
- M. Kocanda and I. Abdel-Motaleb, “DNA Sensing—An Overview of Present Technology and Future Trends,” Proceedings of International Conference on Solid-State and Integrated Circuit Technology, Beijing, 20-23 October 2008, pp. 2536-2540.
- M. Kocanda and I. Abdel-Motaleb, “Development of a DNA Probe Using Barium Strontium Titanate,” Journal of Applied Physics, Vol. 106, No. 12, 2009, pp. 123916-123916-6. http://dx.doi.org/+10.1063/1.3273314
- M. Kocanda and I. Abdel-Motaleb, “DNA Detection Using a Complimentary Metal-Oxide Semiconductor Ring Oscillator Circuit,” Journal of Applied Physics, Vol. 108, No. 7, 2010, pp. 3483947-3483947-3. http://dx.doi.org/+10.1063/1.3273314
- V. M. Goldschmidt, “Geochemische Verteilungsgesetze der Elemente,” Skrifter der Norske Videnskaps-Akad, Vol. 8, No. 3, 1926, pp. 529-533.
- R. Swanepoel, “Determination of the Thickness and Optical Constants of Amorphous Silicon,” Journal of Physics E: Scientific Instruments, Vol. 16, No. 12, 1983, pp. 1214-1216.
- A. K. Bain, et al., “Optical Properties of Barium Strontium Titanate (BST) Ferroelectric Thin Films,” Ferroelectrics Letters Section, Vol. 34, No. 5-6, 2007, pp. 149- 154.
- J. I. Pankove, “Optical Processes in Semiconductors,” Courier Dover Publications, New York, 1990.
- M. L. Sadowski, M. Potemski and M. Grynberg, “Optical Properties of Semiconductor Nanostructures,” Kluwer Academic Publishers, Boston, 2010.
- J. Tauc and A. Menth, “States in the Gap,” Journal of Non-Crystalline Solids, Vol. 8-10, 1972, pp. 569- 585. doi:10.1016/0022-3093(72)90194-9
NOTES
*Corresponding author.

