ABSTRACT

In this paper, a new class of over-relaxed proximal point algorithms for solving nonlinear operator equations with (A,η,m)-monotonicity framework in Hilbert spaces is introduced and studied. Further, by using the generalized resolvent operator technique associated with the (A,η,m)-monotone operators, the approximation solvability of the operator equation problems and the convergence of iterative sequences generated by the algorithm are discussed. Our results improve and generalize the corresponding results in the literature.

1. Introduction

Motivated by an increasing interest in the nonlinear variational (operator) inclusion problems, complementarity problems and equilibrium problems, which provide us a general and unified framework for studying a wide range of interesting and important problems arising in mathematics, physics, engineering sciences, economics finance and other corresponding optimization problems, the proximal point algorithm have been studied by many authors. See, for example, [1-10] and the references therein. Recently, Verma [9] developed a general framework for a hybrid proximal point algorithm using the notion of (A,η)-monotonicity and explored convergence analysis for this algorithm in the context of solving a class of nonlinear inclusion problems along with some results on the resolvent operator corresponding to (A,η)-monotonicity. Furthermore, Verma [10] introduced a general framework for the over-relaxed A-proximal point algorithm based on the A-maximal monotonicity and pointed out “the over-relaxed A-proximal point algorithm is of interest in the sense that it is quite application-oriented, but nontrivial in nature”.

On the other hand, Lan [4] first introduced a new concept of (A,η)-monotone (so called (A,η,m)-maximal monotone [6]) operators, which generalizes the (H,η)-mono-tonicity, A-monotonicity and other existing monotone operators as special cases, and studied some properties of (A,η)-monotone operators and defined resolvent operators associated with (A,η)-monotone operators.

Motivated and inspired by the above works, the purpose of this paper is to introduce and study a new class of over-relaxed proximal point algorithms for approximating solvability of the following nonlinear operator equation in Hilbert space H based on (A,η,m)-monotonicity framework:

Find x ∈ H such that

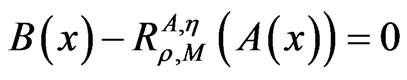, (1)

where A,B:H → H and η:H × H → H are three nonlinear operators, M:H → 2^H is an (A,η,m)-monotone operator with B(H) ∩ domM(·) ≠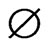and B(H) ∩ domA(·) ≠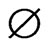, 2^H denotes the family of all the nonempty subsets of H, 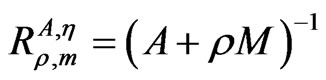is the resolvent operator associated with the multi-valued operator M and ρ > 0 is a constant.

Based on the definition of the resolvent operator, Equation (1) can be written as

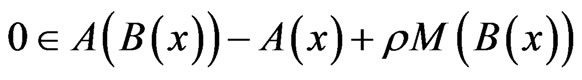, (2)

which was studied by Verma [9,10] when B ≡ I, the identity operator.

We remark that for appropriate and suitable choices of A, B, M, η and H, one can know that the problems (1) and (2) include a number of known a general class of problems of variational character, including minimization or maximization (whether constraint or not) of functions, variational problems, and minimax problems as special cases. For more details, see [1-13] and the references therein, and the following example:

Example 1.1. Consider the following convex optimization problem with bound constraints:

Min f(u),

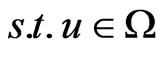, (3)

where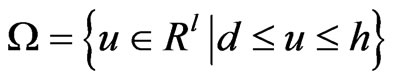, R = (−∞, +∞) and f:Ω → R is convex and continuously differentiable. From the Karush-Kuhn-Tucher conditions, we see that u^* is an optimal solution to the problem (3) if and only if u^* satisfies

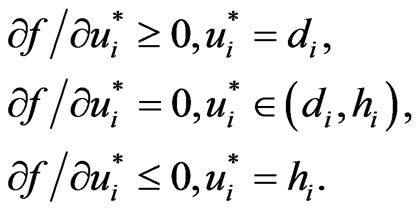(4)

The problem (4) is equivalent to the following variational inequality: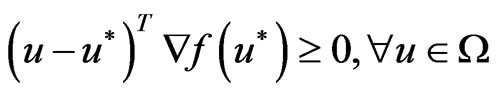, where

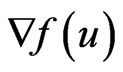is the gradient of f.

2. Preliminaries

In the sequel, we give some concept and lemmas needed later.

Definition 2.1. An operator M^–1, the inverse of M:H → 2^H, is (s,t)-Lipschitz continuous at 0 if for any t ≥ 0, there exist a constant s ≥ 0 and a solution x^* of 0 ∈ M(x) (equivalently x^* ∈ M^–1(0)) such that

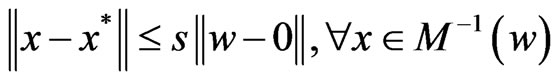where.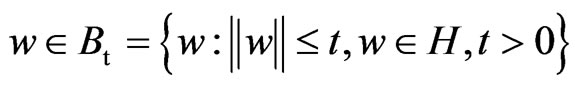

Definition 2.2. Let A, B:H → H and η:H × H → H be single valued operators, and M:H → 2^H be a multi-valued operator. Then i) B is δ-strongly monotone, if there exists constant δ > 0 such that

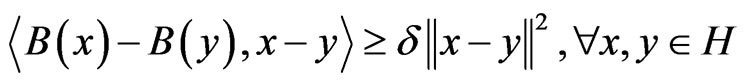which implies that B is δ-expanding, i.e.,

;

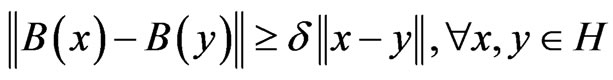ii) A is r-strongly η-monotone, if there exists a positive constant r such that

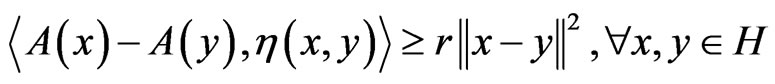iii) A is β-Lipschitz continuous, if there exists a constant β > 0 such that

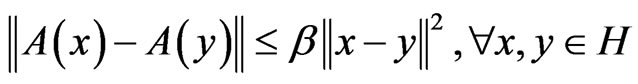iv) η is τ-Lipschitz continuous if there exists a constant τ > 0 such that

.

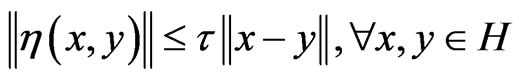v) M is m-relaxed η-monotone if there exists a constant m > 0 such that for all x, y ∈ H, x ∈ M(x) and y ∈ M(y),

;

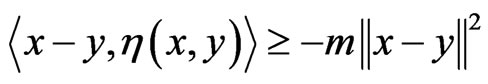vi) M is said to be (A,η,m)-maximal monotone if M is m-relaxed η-monotone and R(A + ρM) = H for every ρ> 0.

Remark 2.1. 1) If m = 0 or A = I or η(x, y) = x − y for all x, y ∈ H, (A,η,m)-maximal monotonicity (so-called (A,η)-monotonicity [4], (A,η)-maximal relaxed monotonicity [3]) reduces to the (H,η)-monotonicity, H-monotonicity, A-monotonicity, maximal η-monotonicity, classical maximal monotonicity (see [1-10]). Further, we note that the idea of this extension is so close to the idea of extending convexity to invexity introduced by Hanson in [11], and the problem studied in this paper can be used in invex optimization and also for solving the variational-like inequalities as a direction for further applied research, see, related works in [12,13] and the references therein.

2) Moreover, operator M is said to be generalized maximal monotone (in short GMM-monotone) if:

i) M is monotone; ii) A + ρM is maximal monotone or pseudomonotone for ρ > 0.

Example 2.1. ([3]) Suppose that A:H → H is r-strongly η-monotone, and f:H → R is locally Lipschitz such that ∂f, the subdifferential, is m-relaxed η-monotone with r − m > 0. Clearly, we have

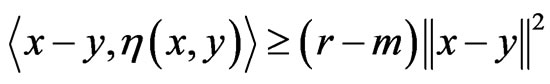where x ∈ A(x) + ∂f(x) and y ∈ A(y) + ∂f(y) for all x, y ∈ H. Thus, A + ∂f is η-pseudomonotone, which is indeed, η-maximal monotone. This is equivalent to stating that A + ∂f is (A,η,m)-maximal monotone.

Lemma 2.1. ([4]) Let η:H × H → H be τ-Lipschitz continuous, A:H → H be a r-strongly η-monotone operator and M:H → 2^H be an (A,η,m)-maximal monotone operator. Then the resolvent operator 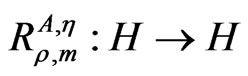defined by

.

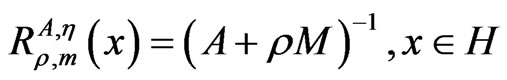is 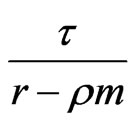-Lipschitz continuous.

Lemma 2.2. Let A, B, η, M and H be the same as in the problem (1). If

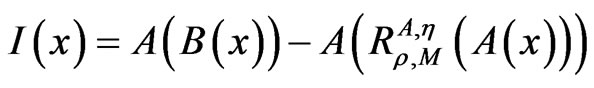
for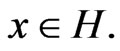, and for all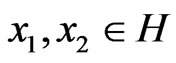, ρ > 0 and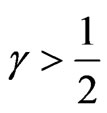

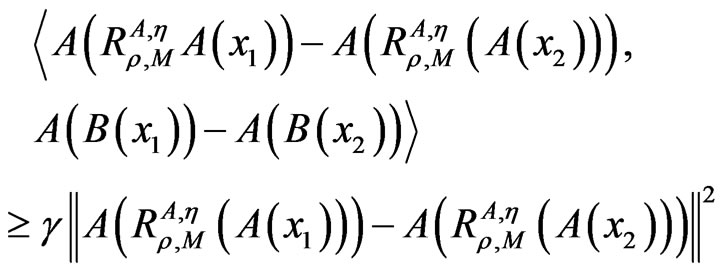
then

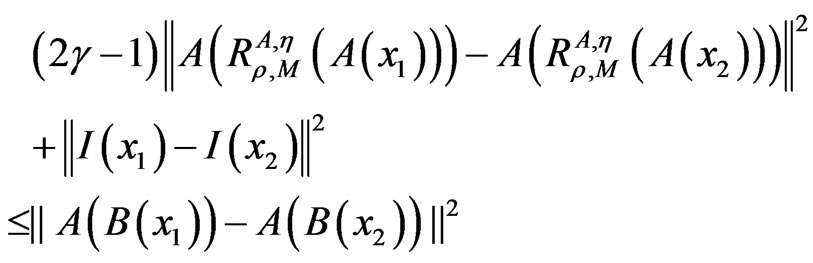Proof. By the assumption, now we know

.

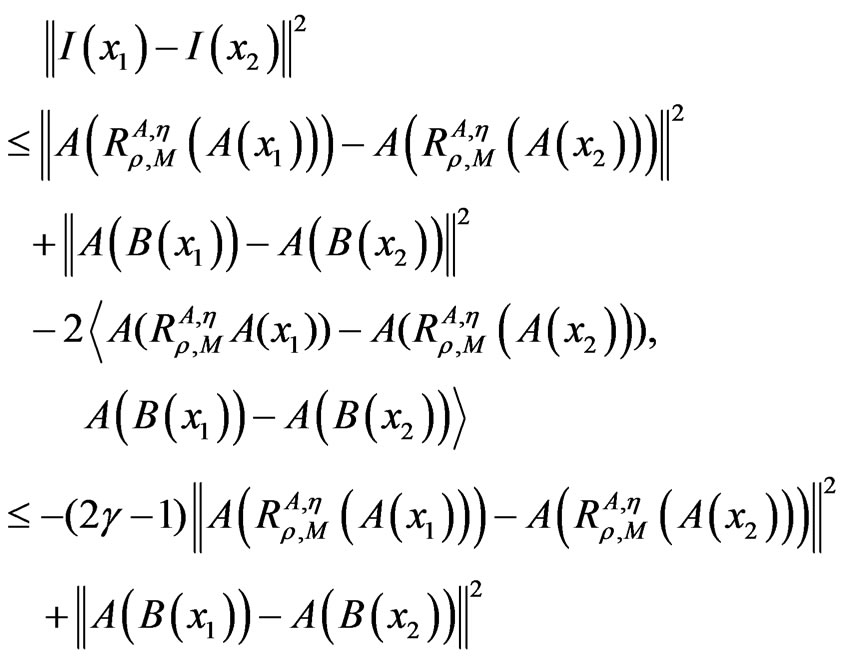This completes the proof.

3. Algorithms and Approximation-Solvability

In this section, we shall introduce a new class of over-relaxed (A,η,m)-proximal point algorithms to approximating solvability of the nonlinear operator Equation (1).

Algorithm 3.1. Step 1. Choose an arbitrary initial point.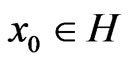

Step 2. Choose sequences {α_n}, {σ_n} and {ρ_n} such that for n ≥ 0, {α_n}, {σ_n} and {ρ_n} are three sequences in [0, ∞) satisfying

.

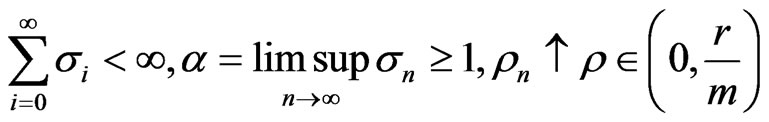Step 3. Let 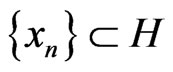be generated by the following iterative procedure

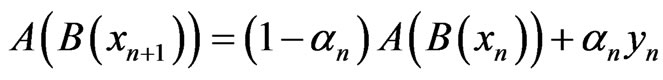, (5)

and y_n satisfies

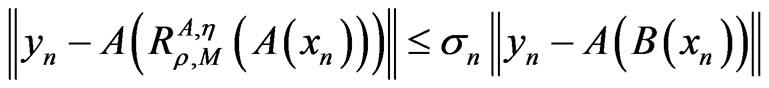where n ≥ 0, 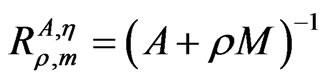and ρ > 0 is a constant.

Step 4. If x_n and y_n (n = 0, 1, 2, ···) satisfy (5) to sufficient accuracy, stop; otherwise, set k: = k + 1 and return to Step 2.

Remark 3.1. We note that Algorithm 3.1 becomes to the algorithm of Theorem 3.2 associated with A-maximal monotonicity in [10] when B ≡ I.

Theorem 3.1. Let A, B, M, η and H be the same as in problem 1). If, in additioni) η is τ-Lipschitz continuous, A is κ-Lipschitz continuous and r-strongly η-monotone, B is β-Lipschitz continuous and δ-strongly monotone with the inverse B^–1 is μ-expanding with μδ ≤ 1;

ii) 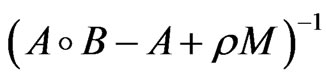is (s,t)-Lipschitz continuous at 0, where 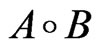is defined by 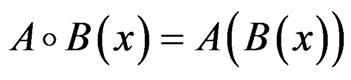for x ∈ H;

iii) for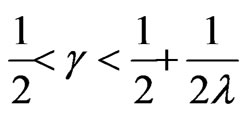

and λ > 0,

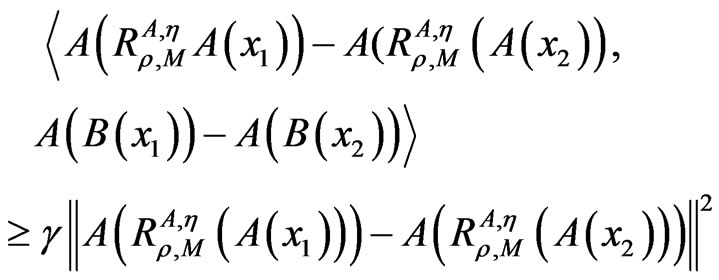
iv) the iterative sequence 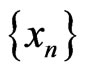generated by Algorithm 3.1 is bounded;

v) there exists a constant ϱ > 0 such that

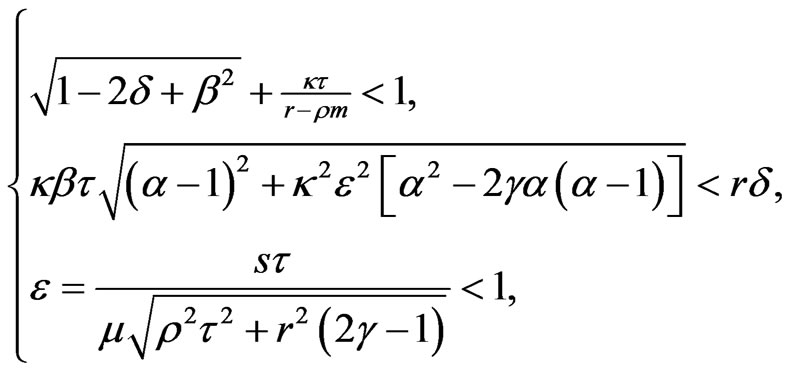(6)

then 1) the nonlinear resolvent operator Equation (1) has a unique solution x^* in H.

2) the sequence {x_n} converges linearly to the solution x^* with convergence rate

.

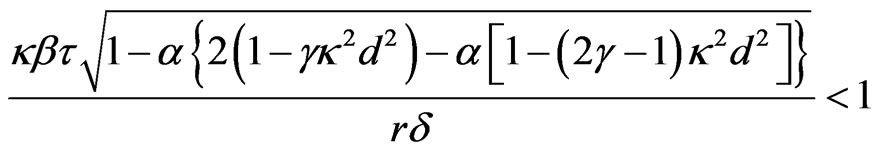Proof. Firstly, for any given ρ > 0, define F:H → H by

.

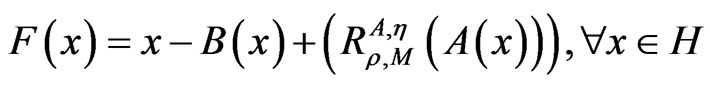By the assumptions of the theorem and Lemma 2.1, for all x, y ∈ H we have

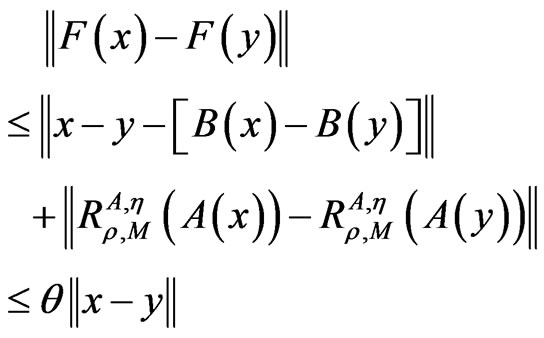
where.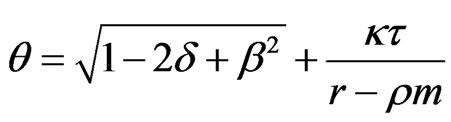

It follows from condition (6) that 0 < 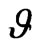< 1 and so F is a contractive mapping, which shows that F has a unique fixed point in X.

Next, we prove the conclusion (2). Let x^* be a solution of problem (1). Then for all ρ_n > 0 and n ≥ 0, we have

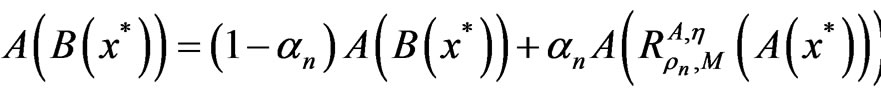, (7)

For 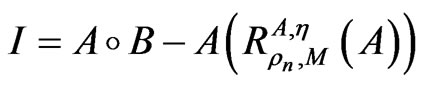and under the assumptions, it follows that I(x_n) → 0(n → ∞). Since

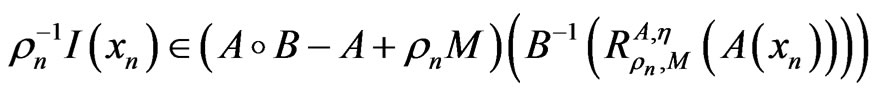this implies

.

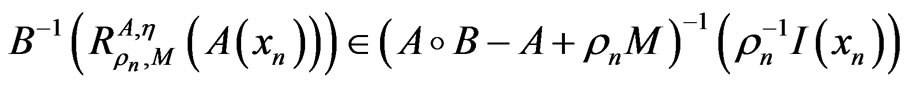Then, applying Lemma 2.2, the strong monotonicity of A, and the Lipschitz continuity of A and η (and hence, A being expanding), and the Lipschitz continuity at 0 of 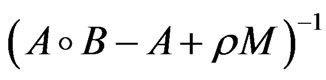by setting 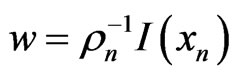and

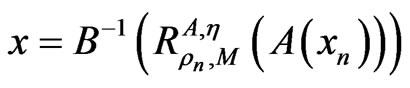we know

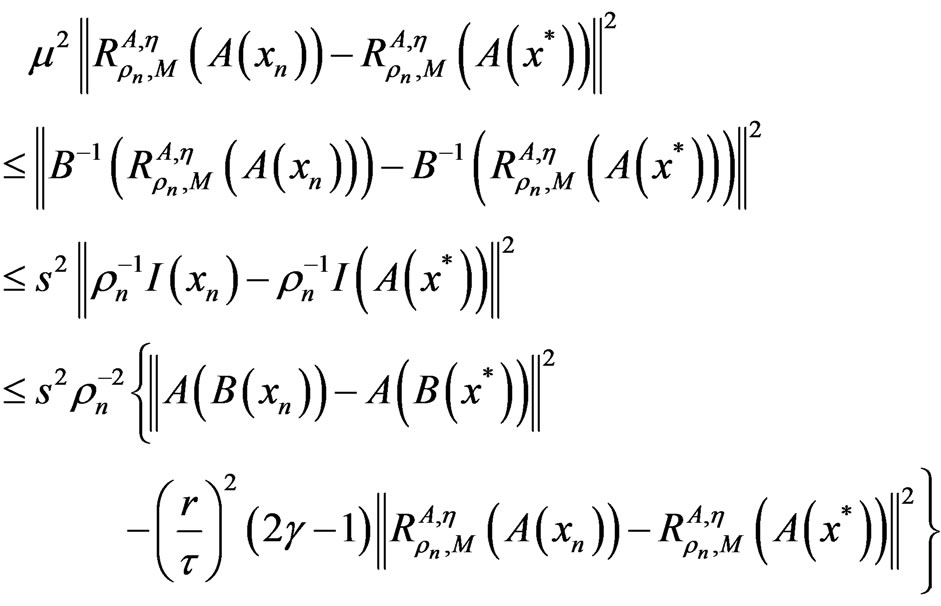which implies

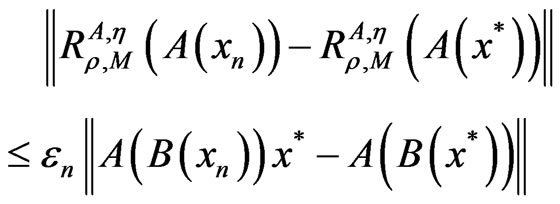, (8)

where.

For n ≥ 0, let

.

By the assumptions of the theorem, (7) and (8), now we find the estimate,

(9)

where

.

Since

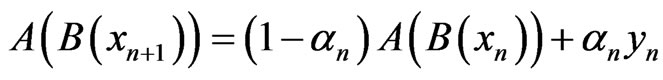we have

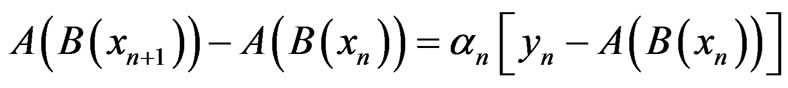
and

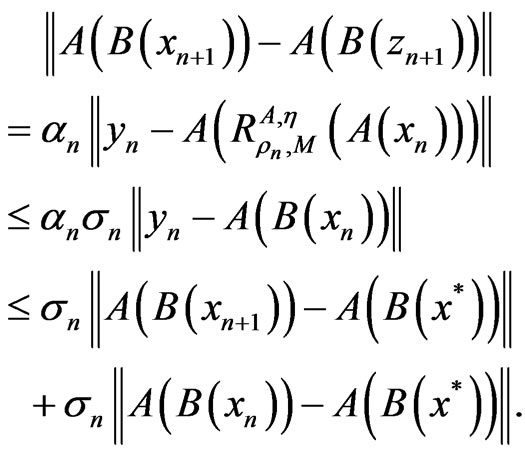(10)

In the sequel, we estimate using (9) and (10) that

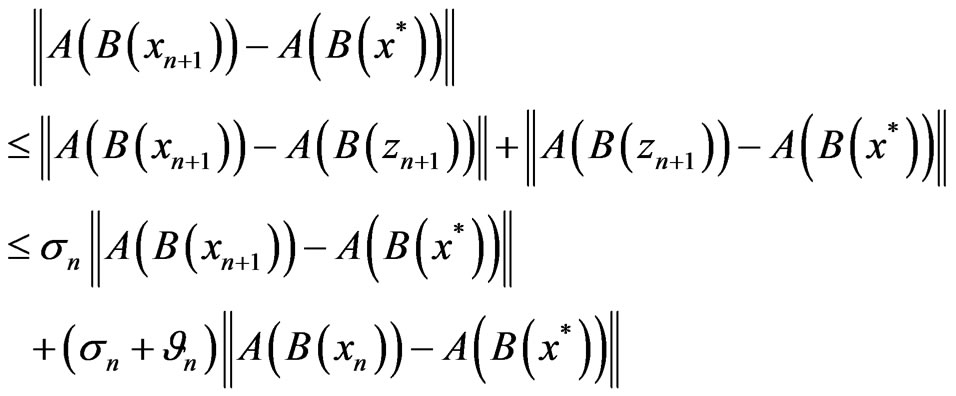
which implies

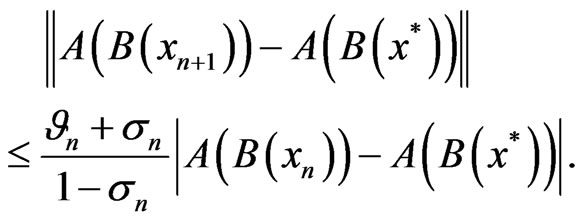(11)

It follows from (11), the strong monotonicity of A and B, and the Lipschitz continuity of A, B and η that for all x, y ∈ H,

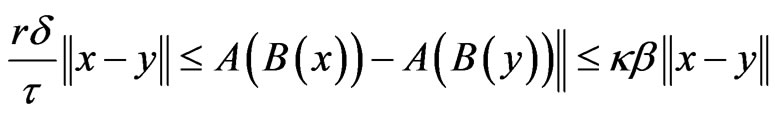
and

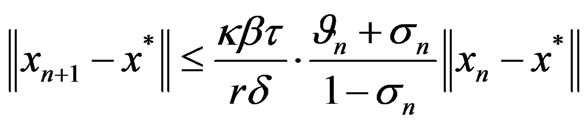(12)

From (12), now we know that the {x_n} converges linearly to a solution x^* for

.

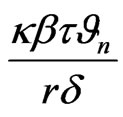Hence, we have

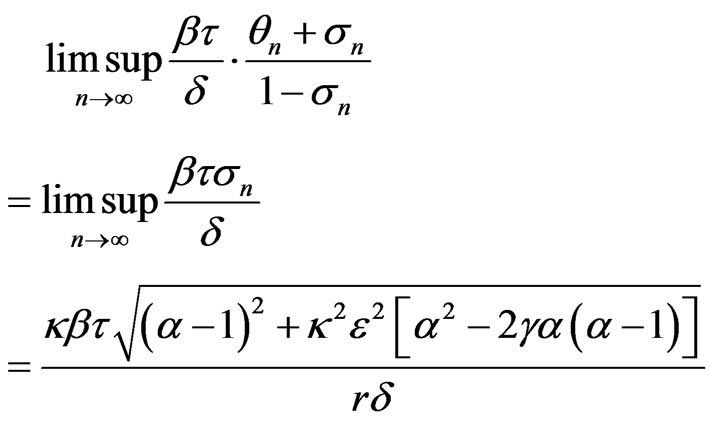
where

,

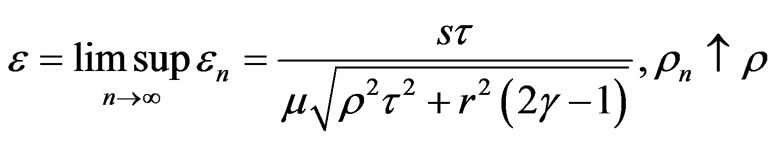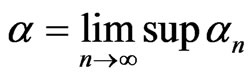. This completes the proof.

Remark 3.2. 1) If B ≡ I or κ = 1 (namely, A is nonexpansive), we have the corresponding results of Theorem 3.1 for nonlinear equation.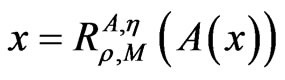

2) By using Lemma 2.1, the convergence analysis of the iterative sequence {x_n} generated by Algorithm 3.1 can be established when the conditions (ii), (iii) and others are not satisfied, that is, the inequality (8) can be replaced by

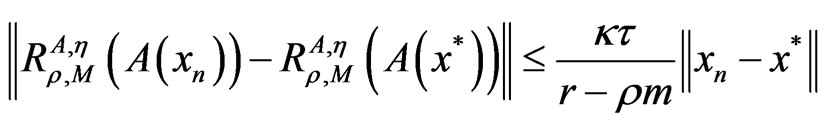
3) The corresponding results can be shown when M is (H,η)-monotonicity, H-monotonicity, A-monotonicity, maximal η-monotonicity and classical maximal monotonicity, respectively. That is, the results presented in this paper improve and generalize the corresponding results of [1,2,9,10].

4. Conclusions

In this paper, we introduce and study a new class of over-relaxed proximal point algorithms for solving the following nonlinear operator equations with (A,η,m)- monotonicity framework in Hilbert spaces: Find x ∈ H such that

.

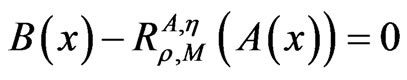Further, by using the generalized resolvent operator technique associated with the (A,η,m)-monotone operators, we investigate the existence of solutions for the operator equation problem and the convergence of iterative sequences generated by the algorithm. The results presented in this paper improve and generalize the corresponding results in the literature.

5. Acknowledgements

This work was supported by the Scientific Research Fund of Sichuan Provincial Education Department (10ZA136) and the Cultivation Project of Sichuan University of Science and Engineering (2011PY01).

REFERENCES