Open Journal of Air Pollution
Vol.05 No.01(2016), Article ID:64482,17 pages
10.4236/ojap.2016.51002
Modeling Submicron Particles Collection in Laminar Forced Convection Gas Flow by a Rectangular Venturi Scrubber
Serge Wendsida Igo1, Kokou N’wuitcha2, Belkacem Zeghmati3, Xavier Chesneau3
1Département Energie, Institut de Recherche en Sciences Appliquées et Technologies (IRSAT/CNRST), Ouagadougou, Burkina Faso
2GPTE-LES, Département de Physique, Université de Lomé, Lomé, Togo
3Laboratoire de Mathématiques et Physique des Systèmes (LAMPS), Perpignan, France

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 January 2016; accepted 11 March 2016; published 14 March 2016
ABSTRACT
Venturi scrubbers are usually used for large particles cleaning in turbulent gaseous flow. In this work, submicron particles scrubbing in laminar forced convection dusty air flow in a rectangular venturi scrubber have been numerically simulated. Hydrodynamics effects and scrubbing process are investigated in detail. Results are presented as flow velocity, axial pressure, streamlines pattern, particles and droplets mass fraction profile, and collect efficiency. They show that venturi scrubbers can be efficient for submicron particles scrubbing. In fact, a better collect efficiency is obtained at high particles-droplets residence time, high ratio droplets concentration/particles concentration, low venturi diameter ratioand low Reynolds numbers. There is a critical Reynolds number value for which the collect efficiency becomes very low and tends to be constant.
Keywords:
Venturi Scrubber, Submicron Particles, Diffusion, Laminar Flow, Collect Efficiency

1. Introduction
Venturi scrubbers are widely used for particles and gaseous collection from industrial exhaust. Their high collection efficiency coupled with low construction and maintenance cost has led to many studies. The large power requirements for operation and large pressure drop across the device are its main drawbacks [1] . These devices consist of channel with three parts: a convergent section, a throat and a divergent section or diffuser. The polluted gas stream is accelerated in the convergent, reaches its maximum velocity in the throat and finally is decelerated in the diverging section. A liquid or an aqueous solution (generally water) is introduced in the venturi to create a spray of droplets for the particles capture. The droplets that captured particles are separated in a device connected to the venturi and the cleaned air is discharged into the atmosphere. In dusty gas scrubbing process by droplets in wet scrubbers, large particles are principally collected by inertial impaction [2] . Their large inertia allows them to leave the gas streamlines to impact onto water drops. Submicron particles which have diameter less than 1µm because their smallness cannot impact onto drops and are collected by brownian diffusion [3] . If a particle follows a streamline which approaches the drop within a distance of the particle radius, the particle is captured by the drop; this kind of collection is called interception. The size of droplets usually lies in the range of 0.1 - 1 mm in diameter [4] . The mode of introduction of the scrubbing liquid has led to three types of venturi: The Pease-Anthony type, the wetted approach type and the ejector type. In the Pease-Anthony venturi type, the scrubbing liquid is introduced into gas stream usually at the throat and sprayed by the high gas velocity. This kind of venturi is the first to be investigated [5] -[8] . Basing on the inertial impaction hypothesis, they have shown that the collect efficiency is depending on gas liquid ratio, venturi geometry, particles and droplets size; And large particles lead to a better collect efficiency. In the wetted approach type, the scrubbing liquid is introduced as a film streaming along the venturi tube walls. Here, droplets are formed due to the gas shear on the liquid film, particularly in the throat and a portion of the liquid remains as a film on the wall. This type of venturi is recommended for hot gas flow, adhesives and corrosives dust [9] -[11] . They have shown that the fraction of liquid streaming as a film influences the collect efficiency and the pressure drop across the device. In the ejector type, the liquid is injected through nozzles by a pressure atomizer at the throat. This king of venturi is efficient for both particles and gaseous pollutants. Moreover, it is ideal for handling sticky or abrasive materials [12] . Despite their dangerousness for human health [13] [14] , submicron particles have not been received much attention in venturi scrubbing process. In these studies cited above, only large particles are considered and the collect hypothesis is only based on inertial impaction. To improve the submicron particles removal efficiency by impaction, others mechanisms such as electrostatic attraction and condensation of water vapor on particles may be used [15] [16] to increase particles size. In others wet scrubbers, diffusion mechanism has been widely studied. Slinn [17] , using dimensional analysis coupled with experimental data, gives correlation for single rain droplet collect efficiency. Jung and Lee [18] derive the collision efficiency due to Brownian diffusion and interception for a multiple fluid sphere system. As seen, diffusive effects have been neglected in venturi scrubbing process.
Recently, Igo et al. [19] [20] performed a numerical code to study the heat and mass transfer in venturi channels. Therefore, the objective of this work is to adapt this code for the submicron particles collection study in venturi scrubbers based on diffusion mechanisms.
2. Problem Formulation
The venturi channel is composed of two plates of sections lengths (L1, L2, L3, L4, L5). The distance between the plates is 2R in the entrance region. The external surface plates are subjected to a constant wall temperature Tw. Temperature To, relative humidity ϕo, downward velocity Uo, concentration of particles Cpo of dusty air flow are supposed to be uniform in the inlet of the venturi channel. A spray of droplets is injected into gas stream at the inlet with an initial concentration Cdo. The venturi wetted walls are submitted to the evaporation of water vapor.
It is assumed that:
―Transfers are two-dimensional and axisymetric;
―The radial pressure gradient component is neglected;
―Dufour and Soret effects are neglected;
―Collects mechanisms are only by diffusion and interception;
―The number of particles collected is equal to the number of droplets lost;
―The mixture composed of air, particles and droplets, is considered as an uncompressible ideal gas.
The dimensionless equations modeling the dusty air flow through the venturi scrubber in the referential (o,x,z) (see Figure 1) are:
Continuity equation
Figure 1. Schematic representation of the studied system in the (O, X, Z) referential.
 (1)
(1)
Axial-momentum equation
 (2)
(2)
Radial-momentum equation
 (3)
(3)
Energy equation
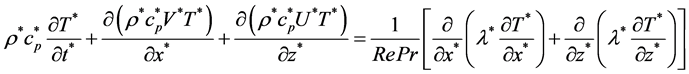 (4)
(4)
Convection-diffusion equation of droplets
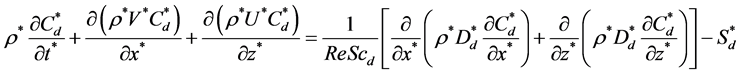 (5)
(5)
Convection-diffusion equation of particles
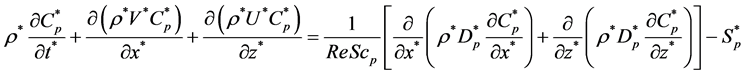 (6)
(6)
Convection-diffusion equation of water vapor
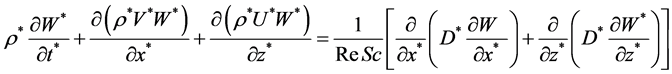 (7)
(7)
Flow rate conservation
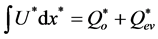 (8)
(8)
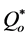 and
and 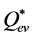 are respectively the inlet gas flow rate and the cumulated evaporated flow rate.
are respectively the inlet gas flow rate and the cumulated evaporated flow rate.
According to Seinfeld and Pandis [21] , the single drop collision efficiency is defined as the number of particles contained within the volume swept by a falling drop that are collected. Note that one droplet sweeps per
unit time a volume of cylinder equal to . So, by writing mass balance for particles, the term source
. So, by writing mass balance for particles, the term source
representing the amount of disappearing of particles can be expressed as:
 (9)
(9)
EF is the overall efficiency collect by a single droplet:
 (10)
(10)
where  and
and 


where α is the packing density, defined as the volume fraction of drops, σ is the viscosity ratio of water to air, 


Using one of the hypothesis formulated above (the number of particles collected is equal to the number of droplets lost), Sd = Sp. Dimensionless terms sources can then be deduced as:


3. Numerical Procedure
3.1. Coordinate Transformation
In order to avoid the non-uniformity of the mesh spacing along the venturi plane, we use a mathematical transformation which transforms the irregular surface of the plate into a straight line:




Therefore, the Equations (2)-(7) can be rewritten in the numerical domain:

where γ, B, κ, χ, and G are defined below (Table 1).
The Equations (1) and (8) are respectively:


Table 1. Expression of coefficients γ, B, κ, χ, and G of Equation (15).
3.2. Initial and Boundaries Conditions
3.2.1. Initial Conditions
"t* < t0; t0 is the dimensionless time when the mixture air-particles-droplets water enters into the venturi:
3.2.2. Boundaries Conditions
At the inlet (ξ = 0, 0 < η < 1)
At the outlet (ξ = L/DH, 0 < η < 1)
At the wall (0 < ξ < L/DH, η = 1)
At the axis of symmetry (0 < ξ < L/DH, η = 0)
We characterize the sensible Nusselt number using the following expression:

The collect efficiency (CE) of the venturi is calculated using the following expression [22] :

The Equation (15) associated to initial and boundaries conditions are discretized using an implicite scheme based on the finite volume method and described by Suhas V. Patankar [23] . The system of algebraic equation deduced from discretisation of the radial momentum equation component, energy and diffusion equations, is for each equation tri-diagonal; so it was solved by Thomas algorithm. The discretisation of the axial momentum equation leads to an algebraic equation system composed of M equations and (M + 1) unknowns variables (U and P). Consequently, it was solved with Gauss algorithm. The convergence was obtained when the following criterion was satisfied:

where
The validation of our numerical code has been carried out by comparing our results with the most closely numerical solution (see Figure 2).
As seen, the discrepancies between our results and those of W. M. Yan and T. F. Lin [24] do not exceed 0.01%.
The computational grid is uniform in the two directions. The step length in each direction and the step time ∆t* = 1.89 × 10−3 are chosen by numerical experiments provided by the stabilities conditions of Thomas and Gauss algorithms. To ensure that the results are grid independent, computations are carried out for several mesh size. The effect of the grid size on the Nusselt number leads to a mesh size of 60 nodes in the η direction and 120 nodes in the ξ direction corresponding to the step lengths (Δη, Δξ). Δη = 17 × 10−3; Δξ = 38 × 10−3. As seen, an increase of the number of nodes by a factor of four does not influence the results significantly. The discrepancies between Nusselt values for mesh size (60 × 120) and mesh size (120 × 240) reported in Table 2 is less than 5%.
4. Results and Discussion
In the present study, calculations were performed for : L1 = 0.1 m, L2 = 0.2 m, L3 = 0.15 m, L4 = 0.3 m, L5 = 0.15 m, R = 0.1 m, To = 293.15 K, Tamb = 298.15 K, dp = 10−2 µm, dd = 100 µm, the ratio droplets concentration/particles concentration (Cdo/Cpo) varies from 1 to 9 and the Reynolds number in the range of 500 to 2000.
Figures 3-7 show the effect of Reynolds number on the velocity and the axial pressure evolution in the venturi. We note that the venturi effect is observed (velocity and pressure gradient evolution are opposite in each section
Table 2. Grid independence.
Figure 2. Validation of the numerical code (To = 20˚C, Tw = 40˚C, ϕo = 50%, Pr = 0.703, Sc = 0.592, Re = 500).
Figure 3. Velocity patterns. Β = 0.25, Re = 500.
Figure 4. Velocity patterns. Β = 0.25, Re = 1500.
Figure 5. Velocity patterns. Β = 0.25, Re = 2000.
Figure 6. Axial pressure gradient versus axial coordinate: effect of Reynolds number. Β = 0.25.
of venturi). In fact, in the converging section there is a continuous increase of the pressure drop due to the acceleration of the mixture air-particles-water droplets velocity resulting of the conversion of the potential energy into kinetic one of the mixture air-particles-water droplets through the venturi throat. Maximum velocity of the mixture air-particles-water droplets is reached in the throat. In addition, the increasing of Reynolds number
Figure 7. Axial velocity versus axial coordinate: effect of Reynolds number. β = 0.25.
increases venturi effect.
Figures 8-10 illustrate the effects of Reynolds number on the flow structure. The change of streamlines is observed for large Reynolds numbers, consequently of the increase of flow velocity. For low Reynolds number, streamlines are parallel to the channel walls. Effects of parameter β on streamlines patterns are presented on Figures 11-13. β equal to 1 is related to a classical vertical channel, streamlines are parallels to the channel walls as showing in Figure 12. When decreasing β, channel is progressively transformed to venturi one. We note that streamlines are very close in the convergent and divergent section, and they are merged in the throat particularly for β equal to 0.35. The flow velocity in the throat is of course more important as β decreases.
An analyse of the effect of the ratio droplets concentration/particles concentration at the inlet (Figures 14-17) show that for equal inlet concentrations, there is no difference between particles and droplets concentration at the venturi exit. This result is the consequence of one of our hypothesis (the number of particles collected equal to the number of droplets lost). We note that the increase of the ratio droplets concentration/particles concentration leads to a better collect of particles because the interactions particles-droplets are depending on the droplets number and increases as the droplets number increases. So the collect efficiency is depending on the ratio (droplet concentration/particles concentration).
Figure 18 show the collect efficiency versus time. Collect efficiency is more important as the particles-drop- lets residence time in the venturi scrubber is rising. This result is in agreement with results of others authors [25] . It is clear that particles staying during a long time in the scrubber enhance their probability to be collected by droplets.
The effect of Reynolds number on the collect efficiency is presented in Figure 19. The collect mechanism according to one of our hypothesis is supposed to be only by diffusion and interception; The collect efficiency decreases as the Reynolds number increases because the particles-droplets residence time particles decreases in the venturi scrubber. We note also, the existence of a critical Reynolds number where the decrease of the collect efficiency is very important and tends to be constant.
Figure 20 show that the collect efficiency increases as β values decreases. This result confirms that in the venturi scrubber, a better mixing particles-water droplets due to the reduction of the channel diameter leads to an improvement of the collect efficiency. Venturi scrubber appears to be more efficient for submicron particles scrubbing than a wall plane channel one.
5. Conclusions
Submicron particles scrubbing in a vertical rectangular venturi scrubber is numerically investigated in the present study. In order to determine the collect efficiency, transfers equations are solved using finite volume
Figure 8. Streamlines patterns. Re = 500, β = 0.25.
Figure 9. Streamlines patterns. Re = 1000, β = 0.25.
Figure 10. Streamlines patterns. Re = 2000, β = 0.25.
Figure 11. Streamlines patterns. Re = 2000, β = 1.
Figure 12. Streamlines patterns. Re = 2000, β = 0.5.
Figure 13. Streamlines patterns. Re = 2000, β = 0.35.
Figure 14. Particles and droplets mass fraction at the venturi outlet versus time. Cdo/Cpo = 1, Re = 500, β = 0.25.
Figure 15. Particles and droplets mass fraction at the venturi outlet versus time. Cdo/Cpo = 3, Re = 500, β = 0.25.
Figure 16. Particles and droplets mass fraction at the venturi outlet versus time. Cdo/Cpo = 6, Re = 500, β = 0.25.
Figure 17. Particles and droplets mass fraction at the venturi outlet versus time. Cdo/Cpo = 9, Re = 500, β = 0.25.
Figure 18. Collect efficiency versus time. Cdo/Cpo = 9, Re = 500, β = 0.25.
Figure 19. Collect efficiency versus Reynolds number. Cdo/Cpo = 1, β = 0.25.
Figure 20. Collect efficiency versus β. Re = 500, Cdo/Cpo = 9.
method, Gauss and Thomas algorithm. The effects of inlet Reynolds number, flow structure, inlet ratio droplet concentration/particles concentration, venturi diameter ratio and species residence time on the collect efficiency are been investigated in details. The major results are:
―A venturi scrubber is more efficient for submicron particles scrubbing than a wall plane channel one.
―Collect efficiency is better at low Reynolds numbers, high ratio droplet concentration/particles diameter, low venturi diameter ratio and high residence time of species.
―There is a critical Reynolds number, where the collect efficiency decreases significantly and tends to be constant.
Acknowledgements
The authors acknowledge the embassy of France in Burkina Faso for his financial support.
Cite this paper
Serge WendsidaIgo,KokouN’wuitcha,BelkacemZeghmati,XavierChesneau, (2016) Modeling Submicron Particles Collection in Laminar Forced Convection Gas Flow by a Rectangular Venturi Scrubber. Open Journal of Air Pollution,05,10-26. doi: 10.4236/ojap.2016.51002
References
- 1. Viswanathan, S. (1997) Modeling of Venturi Scrubber Performance. Industrial & Engineering Chemistry Research, 36, 4308-4317.
http://dx.doi.org/10.1021/ie970235s - 2. Chate, D.M and Kamra, A.K. (1997) Collection Efficiencies of Large Water Drops Collecting Aerosol Particles of Various Densities. Atmospheric Environment, 31, 1631-1635.
http://dx.doi.org/10.1016/S1352-2310(96)00338-X - 3. Dullien, F.A.L. (1989) Industrial Gas Cleaning. Academic Press, New York.
- 4. Park, S.H., Jung, C.H., Jung, K.R., Lee, B.K. and Lee, K.W. (2005) Wet Scrubbing of Polydisperse Aerosols by Freely Falling Droplets. Aerosols Science, 36, 1444-1458.
http://dx.doi.org/10.1016/j.jaerosci.2005.03.012 - 5. Johnstone, H.F., Fied, R.B. and Tassler, M.C. (1954) Gas Absorption and Aerosol Collection in Venturi Atomiser. Industrial and Engineering Chemistry, 45, 1602-1608.
- 6. Calvert, S. (1970) Venturi and Other Atomizing Scrubbers Efficiency and Pressure Drop. AICHE Journal, 16, 392-396. http://dx.doi.org/10.1002/aic.690160315
- 7. Boll, R.H. (1973) Particles Collection and Pressure Drop in Venturis Scrubbers. Industrial & Engineering Chemistry Fundamentals, 12, 40-50.
http://dx.doi.org/10.1021/i160045a008 - 8. Leith, D.E. and Cooper, D.W. (1980) Venturi Scrubbers Optimization. Atmospheric Environment, 44, 657-664.
http://dx.doi.org/10.1016/0004-6981(80)90049-9 - 9. Azzopardi, B.J. and Govan, A.H. (1984) The Modelling of Venturi Scrubbers. Filtration & Separation, 21, 196-200.
- 10. Pulley, R.A. (1997) Modelling the Performance of Venturi Scrubbers. Chemical Engineering Journal, 67, 9-18.
http://dx.doi.org/10.1016/S1385-8947(97)00014-4 - 11. Rahimi, A., Taheri, M. and Fathikaljahi, J. (2005) Mathematical Modelling of Non-Isothermal Venturi Scrubbers. The Canadian Journal of Chemical Engineering, 83, 401-408.
http://dx.doi.org/10.1002/cjce.5450830302 - 12. Gamisans, X., Sarrà, M. and Lafuente, F.J. (2004) Fluid Flow and Pumping Efficiency in an Ejector-Venturi Scrubber. Chemical Engineering and Processing, 43, 127-136.
http://dx.doi.org/10.1016/S0255-2701(03)00104-1 - 13. Clyde, M.A., Guttorp, P. and Sullivan, E. (2000) Effects of Ambient Fine and Coarse Particles on Mortality in Phoenix, Arizona. NRCSE Technical Report Series, No. 40, 1-14.
- 14. Vermont Air Pollution Control Division (1997) Fine Particles: The Microscopic Menace. Air Matters, 2, 1-8.
- 15. Bologa, A., Paur, H. and Wascher, T. (2001) Electrostatic Charging of Aerosol as a Mechanism of Gas Cleaning from Submicron Particles. Filtration & Separation, 38, 26-30.
http://dx.doi.org/10.1016/S0015-1882(01)80581-4 - 16. Huang, C.-H., Tsai, C.-J. and Wang, Y.-M. (2007) Control Efficiency of Submicron Particles by an Efficient Venturi Scrubber System. Journal of Environmental Engineering, 133, 454-461.
http://dx.doi.org/10.1061/(ASCE)0733-9372(2007)133:4(454) - 17. Slinn, W.G.N. (1983) Precipitation Scavenging. Atmospheric Sciences and Power Production—1979. Division of Biomedical Environmental Research, US Department of Energy, Washington DC.
- 18. Jung, C.H. and Lee, K.W. (1998) Filtration of Fine Particles by Multiples Liquid Drop and Gas Bubble Systems. Aerosols Sciences and Technology, 29, 389-401.
http://dx.doi.org/10.1080/02786829808965578 - 19. Igo, S.W., Kokou, N., Ouédraogo, I., Dieudonné, J.B. and Belkacem, Z. (2014) Numerical Simulation of Laminar Forced Convection Air Flow in a Rectangular Venturi Channel. Journal of Engineering Studies and Research, 20, 101-107.
- 20. Igo, S.W., Dieudonné, J.B., Palm, K., Kokou, N., Belkacem, Z. and Chesneau, X. (2011) Laminar Forced Convection Heat and Mass Transfer in Venturi Tube with Wetted Walls. Frontiers in Heat and Mass Transfer, 2, Article ID: 033007.
http://dx.doi.org/10.5098/hmt.v2.3.3007 - 21. Seinfeld, J.H. and Pandis, S.N. (1998) Atmospheric Chemistry and Physics: From Air Pollution to Climate Change. Wiley, New York.
- 22. Mohebbi, A., Taheri, M., Fathikaljahi, J. and Talaie, M.R. (2003) Simulation of an Orifice Scrubber Performance Based on Eulerian/Lagragian Method. Journal of Hazardous Materials, 100, 13-25.
http://dx.doi.org/10.1016/S0304-3894(03)00066-9 - 23. Suhas, V.P. (1980) Numerical Heat Transfer and Fluid Flow. Hemisphere Publishing Corporation, New York.
- 24. Yan, W.M. and Lin, T.F. (1998) Combined Heat and Mass Transfer in Laminar Forced Convection Channel Flows. International Communications in Heat and Mass Transfer, 15, 333-343.
http://dx.doi.org/10.1016/0735-1933(88)90034-6 - 25. Koo, J., Hong, J., Lee, H. and Shin, S. (2010) Effect of the Particle Residence Time and the Spray Droplet Size on the Particle Removal Efficiencies in a Wet Scrubber. Heat and Mass Transfer, 46, 649-656.
http://dx.doi.org/10.1007/s00231-010-0611-9
Nomenclature



















































