Open Journal of Air Pollution
Vol.04 No.03(2015), Article ID:59238,9 pages
10.4236/ojap.2015.43011
The Influence of Eddy Diffusivity Variation on the Atmospheric Diffusion Equation
A. A. Marrouf1, Khaled S. M. Essa1, Maha S. El-Otaify1, Adel S. Mohamed2, Galal Ismail2
1Department of Mathematics and Theoretical Physics, Atomic Energy Authority, Cairo, Egypt
2Department of Mathematics, Faculty of Science, Zagazig University, Zagazig, Egypt
Email: a4_mmarrouf@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 May 2015; accepted 25 August 2015; published 28 August 2015
ABSTRACT
The advection diffusion equation was solved analytically using separation of variables technique, considering first the wind speed and eddy diffusivity as constants; second as variables dependent on vertical height z. Comparison between predicted two models and observed concentration on Inshas, Cairo (Egypt) is done.
Keywords:
Advection-Diffusion Equation, Separation of Variable Technique, Pollution, Concentrations

1. Introduction
Air pollutants released from various sources affect directly or indirectly man and his environment. Air pollutants emitted from different sources are transported dispersed or deposited my meteorological and topographical conditions. Dispersion of pollutants in the atmosphere is governed by the following dominant mechanisms [1] , mean air flow that transports the pollutants downwind and turbulent velocity fluctuations that disperse the pollutants in all directions. Under moderate to strong winds, the continuously emitted pollutants from a cone- shaped plume in the downwind direction of the source. In this case, advection in the mean wind direction dominates over diffusion and dispersion in the crosswind and vertical directions is assumed to be non-Gaussian. Along-wind diffusion is particularly important near the leading edge of the plume, where uncontaminated fluid from upwind mixes with the mass initially released [2] .
Analytical solutions of the advection-diffusion equation are usually obtained just for stationary conditions and by making strong assumptions about the eddy diffusivity coefficients (K) and wind speed profiles (U). They are assumed as constant throughout the whole Atmospheric Boundary Layer (ABL) or follow a power law [3] - [6] . Moreira et al. presented a solution of the advection-diffusion equation based on the Laplace transform considering the ABL as a multilayer system [7] . Number of dispersion regulatory models includes improved dispersion algorithms in terms of fundamental scaling parameters [8] - [11] . Gryning et al. suggested a modeling approach composed by individual models [12] ; each one based the specific turbulent structure of the regimes in the ABL, following [13] . The models give the crosswind-integrated concentrations at the ground, for non-buoyant releases from a continuous point source. They are limited to horizontally homogeneous conditions and travel distances less than 10 km.
Palazzi et al. have proposed a simple model for studying the diffusion of substances emitted in steady-state releases of short duration assuming the presence of an infinite mixing layer [14] . The Gaussian models, which are the best known and most widely used, are based on a solution of the two-dimensional advection equation where both the wind and exchange coefficients are assumed to be constant. The Gaussian model solution is forced to represent an inhomogeneous atmosphere through empirical dispersion parameters [15] .
In this study, we have formulated a mathematical model for dispersion of air pollutants in moderated winds by taking into account the diffusion in vertical height direction and advection along the mean wind. The eddy diffusivity and wind speed are assumed to be constant. An analytical solution has been obtained for the resulting advection-diffusion equation with the physically relevant boundary conditions. The moderate data collected during the convective conditions. Nine experiments were conducted at Inshas site, Cairo-Egypt [16] , which used to investigate the analytical solution.
2. Mathematical Treatment
The dispersion of pollutants in the atmosphere is governed by the basic atmospheric diffusion equation. Under the assumption of incompressible flow, atmospheric diffusion equation based on the Gradient transport theory can be written in the rectangular coordinate system as:
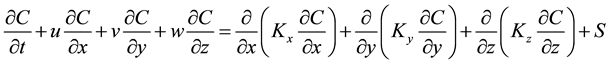 (1)
(1)
where C is the mean concentration of a pollutant (Bq/m3), (µg/m3) and (ppm); S is the source term, respectively; (u, v, w) and (kx, ky, kz) are the components of wind and diffusivity vectors in x, y and z directions, respectively, in an Eulerian frame of reference.
The following assumptions are made in order to simplify Equation (1):
1) Steady-state conditions are considered, i.e.
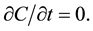
2) As the vertical velocity is much smaller than the horizontal one in x-direction, the term
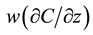 is neglected.
is neglected.
3) x-axis is oriented in the direction of mean wind u = U and U much greater than the wind speed
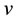 in y-direction the term
in y-direction the term
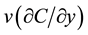 is neglected).
is neglected).
4) Source (physical/chemical) pollutants are ignored so that S = 0.
With the above assumptions, Equation (1) reduces to:
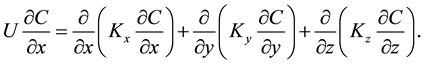 (2)
(2)
The advection term in x direction is larger than the diffusion in x direction then we will neglect the diffusion term in x direction,
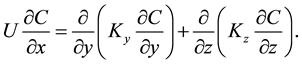 (3)
(3)
Equation (3) is solved together with the following boundary conditions.
The is assumed to be a perfectly total absorption i.e.,
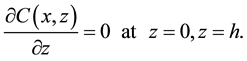 (4)
(4)
The pollutant is totally penetrate through the top of the inversion/mixed layer located at height h, i.e.
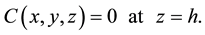 (5)
(5)
A continuous point source with strength Q is assumed to be located at the point (0, ys, zs), i.e.
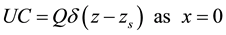 (6)
(6)
where
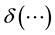 is Dirac’s delta function.
is Dirac’s delta function.
Far away from the source, the concentration decreases to zero, i.e.
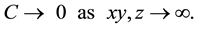 (7)
(7)
2.1. Variable Eddy Diffusivity and Wind Speed
Here we will use Equation (3), considering the wind speed U as linear of z:
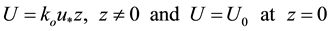 (8)
(8)
and eddy diffusivity kz is expressed as functions of power law of z as:
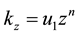 (9)
(9)
where ko is Von-Karmen constant and u∗ is the friction velocity. Where u1 is turbulence intensity.
Also after integrating Equation (3) with respect to y from (−∞ to ∞), Equation (2) becomes:
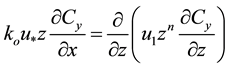 (10)
(10)
which is simply reads:
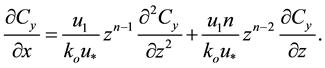 (11)
(11)
One can solve the two-dimensional partial differential Equation (11) analytically by using the separation of variables technique. We take the solution of Equation (11) of the form:

Differentiating Equation (12) partially with respect to x and z and substituting in Equation (11), we get two ordinary differential equations in the variables X and Z as follows:

and

where λ2 is a constant,

The general solution of Equation (13) is given by

where

Equation (14) becomes:

Equation (16) which simply reads:

where
The solution of Equation (14) is obtained in different boundary conditions as follows:
Equation (10) along with the following boundary condition corresponding to Equation (4) and Equation (5):

On changing the dependent Z and independent z variables in Equation (16) by means of the substitutes:

Equation (17) is a Bessel equation and has a solution [17] :

where jµ and J−µ the Bessel functions of first kind of order µ and −µ, respectively, A and B are constants, application of the boundary condition Equation (18) at z = 0 in Equation (20) yields B = 0 and condition z = h Equation (18) gives rise:

Equation (21) this represents Storm-Liouville Eigen value problem which have the corresponding Eigen functions:

The general of Equation (10) is obtained by using Equation (15), Equation (21) and Equation (22) as:

where

Estimation of the coefficients Aα’s for crosswind integrated concentrations: The source at x = 0, Equation (6) gives:

To determine the values of

Multiplying Equation (24) by


Substituting


In which


2.2. Eddy Diffusivity and Wind Speed as Constant
Here we will use Equation (3), considering the wind speed U and eddy diffusivity

Also after integrating Equation (3) with respect to y from (−∞ to ∞), Equation (2) becomes:

which is simply reads:

One can solve the two-dimensional partial differential Equation (29) analytically by using the separation of variables technique. We take the solution of Equation (29) of the form:

Differentiating (30) partially with respect to x and z and substituting in Equation (29), we get two ordinary differential equations in the variables F(x) and G(x) as follows:

and

where

The general solution of Equation (31) is given by

where

Equation (32) becomes:

which have solution

where A and B are constant.
Then from Equation (33) and Equation (35) the general solution

By differentiate Equation (36) with respect to z and applying the boundary conditions we get:

Appling the boundary condition Equation (4) on Equation (37) which gives


Again apply the boundary condition Equation (6) leads to

Substituting A in Equation (38), the final solution is given as follows:

In the Previous section we used the wind speed and eddy diffusivity as functions in the vertical height z, and we had the solution Equation (26). Now we have two forms of the solutions Equation (26) and Equation (40).
3. Applications
3.1. Source Data
The diffusion data for the estimating were gathered during 135I isotope tracer nine experiments in moderate wind with unstable conditions at Inshas, Cairo. During each run, the tracer was released from source has height 43 m for twenty four hours working, where the air samples were collected during half hour at a height 0.7 m.
We collected air samples from 92 m to 184 m around the source in AEA, Egypt. The study area is at, dominated by sand soil with poor vegetation cover. The air samples collected were analyzed in Radiation Protection Department, NRC, AEA, Cairo, Egypt using a high volume air sampler with 220 V = 50 Hz bias [10] . Meteorological data have been provided by the measurements done at 10 and 60 m. Table 1 gives the data information
Table 1. Meteorological data of the nine convective test runs at Inshas site in March and May 2006.
about the diffusion tests and the wind vectors. In addition, it contains values of vertical velocity scale (w*) and mixing height (zi). The data from these nine unstable test runs have been utilized for the following analysis.
Table 1 gives information about the diffusion tests and the wind vectors. In addition, it contains values of the vertical velocity scale (w*).
3.2. Model Parameters
For the concentration computations, we require the knowledge of wind speed, wind direction, source strength, the dispersion parameters, mixing height and the vertical scale velocity. Wind speeds are greater than 3 m/s most of the time even at 10 m level. Further the variation wind direction with time is also visible. The analytical expressions depend upon downwind distance, vertical distance and atmospheric stability. The atmospheric stability has been calculated from Monin-Obukhov length scale (1/L) [19] based on friction velocity, temperature, and surface heat flux.
4. Results and Discussion
The concentration is computed using data collected at vertical distance of a 30 m multi-level micrometeorological tower. In all a test runs were conducted for the purpose of computation. The concentration at a receptor can be computed in the following way:
Applying formula Equation (26) which contains the wind sped and eddy diffusivity as variable and Equation (40) which contains the wind sped and eddy diffusivity as constant at y = 0.0 for half hourly averaging.
Table 2 contains the observed concentrations Bq/m3 and proposed concentrations in bounded and unbounded cases.
As an illustration, results computed from these approaches are shown in Table 2, for nine typical tests conducted at Inshas site, Cairo-Egypt [16] . This table shows that the predicted concentrations for 135I using Equation (26) is very near to the observed concentration more than the predicted concentrations using Equation (40), because the eddy diffusivity and the wind speed were used as constants, on the other hand the eddy diffusivity and the wind speed had been used as functions in vertical height z, in Equation (26).
Figure 1 shows the variation of predicted and observed concentration of 135I with the downwind distance. One gets good agreement between observed and predicted concentration Equation (26) more than predicted concentration Equation (40).
Figure 2 shows that the predicted concentrations which are estimated from Equation (26) and Equation (40) are a factor of two with the observed concentration.
Table 2. Observed and predicted concentrations for run 9 experiments.
Figure 1. Maximum computed concentrations compared with observed maximum value for each test run Equation (26) and Equation (40).
Figure 2.Diagram of predicted model for Equation (26) and Equation (40) with corresponding observation. Solid lines indicate one to one and dashed lines a factor of two.
5. Statistical Method
1) Normalized mean square error (NMSE): It is an estimator of the overall deviations between predicted and observed concentrations. Smaller values of NMSE indicate a better model performance. It is defined as:
2) Fractional bias (FB): It provides information on the tendency of the model to overestimate or underestimate the observed concentrations. The values of FB lie between −2 and +2 and it has a value of zero for an ideal model. It is expressed as:
3) Correlation coefficient (R): It describes the degree of association between predicted and observed concentrations and is given by:
4) Fraction within a factor of two (FAC2) is defined as:
FAC2 = fraction of the data for which
where σp and σo are the standard deviations of Cp and Co respectively. Here the over bars indicate the average over all measurements (N∙m). A perfect model would have the following idealized performance: NMSE = FB = 0 and
From the statistical method of Table 3, we find that the predicted concentrations Equation (26) and Equation (40) for 135I lies inside factor of 2 with observed data. Regarding to NMSE, FB and COR the predicted concentrations Equation (26) for 135I is better with observed data more than predicted concentrations Equation (40), this is because in model of Equation (26) the wind speed and eddy diffusivity were used as functions in the vertical height z, contrast that Equation (40) the wind speed and eddy diffusivity were used as constant.
6. Conclusions
In this paper, we have formulated a mathematical model for dispersion of air pollutants in moderated winds. The diffusion in vertical height direction and advection along the mean wind are taking into account. The eddy diffusivity and the wind speed are assumed to be constant times and variable times. The analytical model is compared with data collected from nine experiments conducted at Inshas, Cairo (Egypt). One gets the predicted concentration Equation (40) that is in poor agreement with the corresponding observation in contrast Equation (26) that gives good agreement with the corresponding observation. Because the eddy diffusivity and the wind speed were used as constants (Equation (40)). On the other hand, the eddy diffusivity and the wind speed had been used as functions in vertical height “z”, in Equation (26).
Statistical method also shows that wind speed and eddy diffusivity are taken as a variable better than as a constant.
Cite this paper
A. A.Marrouf,Khaled S. M.Essa,Maha S.El-Otaify,Adel S.Mohamed,GalalIsmail, (2015) The Influence of Eddy Diffusivity Variation on the Atmospheric Diffusion Equation. Open Journal of Air Pollution,04,109-118. doi: 10.4236/ojap.2015.43011
References
- 1. Wark, K. and Waner, C.F. (1981) Air Pollution. Its Origin and Control. Harper and Row, New York.
- 2. Wilson, D.J. (1981) Along-Wind Diffusion of Source Transients. Atmospheric Environment, 15, 489-495.
http://dx.doi.org/10.1016/0004-6981(81)90179-7 - 3. Van Ulden, A.P. and Hotslag, A.A.M. (1985) Estimation of Atmospheric Boundary Layer Parameters for Diffusion Applications. Journal of Climate and Applied Meterology, 24, 1196-1207.
http://dx.doi.org/10.1175/1520-0450(1985)024<1196:EOABLP>2.0.CO;2 - 4. Pasquill, F. and Smith, F.B. (1983) Atmospheric Diffusion. 3rd Edition, Wiley, New York.
- 5. Seinfeld, J.H. (1986) Atmospheric Chemistry and Physics of Air Pollution. Wiley, New York.
- 6. Sharan, M., Singh, M.P. and Yadav, A.K. (1996) Mathematical Model for Atmospheric Dispersion in Low Winds with Eddy Diffusivities as Linear Functions of Downwind Distance. Atmospheric Environment, 30, 1137-1145.
http://dx.doi.org/10.1016/1352-2310(95)00368-1 - 7. Moreira, D.M., Tirabassi, T. and Carvalho, J.C. (2005) Plume Dispersion Simulation in Low Wind Conditions in the Stable and Convective Boundary Layers. Atmospheric Environment, 30, 3646-3650.
http://dx.doi.org/10.1016/j.atmosenv.2005.03.004 - 8. Cosemans, G., Kretzchmar, J. and Maes, G. (1992) The Belgian Emission Frequency Distribution Model IFDM. Proceedings of the DCAR Workshop on Objectives for Next Generation of Practical Short-Range Atmospheric Dispersion models, Riso, 149-150.
- 9. Olesen, H.R., Lofstorm, P., Berkowicz, R. and Jensen, A.B. (1992) An Improved Dispersion Model for Regulatory Use: The OML Model. In: van Dop, H. and Kallos, G., Eds., Air Pollution Modeling and Its Application IX, Plenum Press, New York.
http://dx.doi.org/10.1007/978-1-4615-3052-7_3 - 10. Hanna, S.R. and Chang, J.C. (1993) Hybrid Plume Dispersion Model (HPDM) Improvements and Testing at Three Field Sites. Atmospheric Environment, 27A, 1491-1508.
http://dx.doi.org/10.1016/0960-1686(93)90135-L - 11. Carruthers, D.J., Edmunds, H.A., Ellis, K.L., McHugh, C.A., Davies, B.M. and Thomson, D.J. (1995) The Atmospheric Dispersion Modeling System (ADMS): Comparisons with Data from the Kincaid Experiment. International Journal of Environment and Pollution, 5, 213-228.
- 12. Gryning, S.E., Holtslag, A.A.M., Irwin, J.S. and Sivertsen, B. (1987) Applied Dispersion Modeling Based on Meteorological Scaling Parameters. Atmospheric Environment, 21, 79-89.
http://dx.doi.org/10.1016/0004-6981(87)90273-3 - 13. Holtslag, A.A.M. and Nieuwstadt, F.T.M. (1986) Scaling the Atmospheric Boundary Layer. Meterology, 36, 201-209.
http://dx.doi.org/10.1007/bf00117468 - 14. Palazzi, E., De Faveri, M., Fumarola, G. and Ferraiolla, G. (1982) Diffusion from a Steady Source of Short Duration. Atmospheric Environment, 16, 2785-2790.
http://dx.doi.org/10.1016/0004-6981(82)90029-4 - 15. Essa, K.S.M., Mina, A.N. and Higazy, M. (2011) Analytical Solution of Diffusion Equation in Two Dimensions Using Two Forms of Eddy Diffusivities. Romanian Journal of Physics, 56, 1228-1240.
- 16. Essa, K.S.M. and El-Otaify, M.S. (2007) Mathematical Model for Hermitized Atmospheric Dispersion in Low Winds with Eddy Diffusivities Linear Functions Downwind Distance. Meteorology and Atmospheric Physics, 96, 265-275.
http://dx.doi.org/10.1007/s00703-006-0208-5 - 17. Irving, J. and Mullineux, N. (1959) Mathematics in Physics and Engineering. Academic Press, New York.
- 18. Gradshteyn, I.S. and Ryzhik, I.M. (1965) Table of Integrals, Series and Products. 7th Edition, Academic Press, New York, 1160.
- 19. Golder, D. (1972) Relation among Stability Parameters in the Surface Layer. Boundary Layer Meteorology, 3, 47-58.
http://dx.doi.org/10.1007/BF00769106 - 20. Essa, K.S.M., Mubarak, F. and Khadra, S.A. (2005) Comparison of Some Sigma Schemes for Estimation of Air Pollutant Dispersion in Moderate and Low Winds. Atmospheric Science Letters, 6, 90-96.
http://dx.doi.org/10.1002/asl.94










