Journal of Financial Risk Management
Vol.06 No.03(2017), Article ID:78356,9 pages
10.4236/jfrm.2017.63018
Co-Movement and Interaction Effects across the Monetary, Foreign Exchange and Stock Markets: Evidence from China
Xuejin Zhao1, Han Zhang2
1School of Business Administration, South China University of Technology, Guangzhou, China
2Shenzhen Central Sub-Branch of the People’s Bank of China, Shenzhen, China

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 11, 2017; Accepted: August 8, 2017; Published: August 11, 2017
ABSTRACT
This paper investigates the issue of co-movement and interaction among the monetary, foreign exchange and stock markets by employing the data from China’s financial markets. Based on the ICA-EGARCH-M model, we explore the volatility spillover effects so as to illustrate the overall co-movements across financial markets. Furthermore, in order to observe the multi-market dynamic relationship variation process, we calculate the dynamic correlation coefficients with the AG-DCC-MGARCH model. Our findings provide both static and dynamic evidence on the co-movement and interaction effects of financial markets which may lead to the systemic financial risk.
Keywords:
Co-Movement, Interaction, Financial Markets, Spillover Effect, Dynamic Correlation

1. Introduction
A domino effect exists in the financial markets, which is a complex system of multiple levels with cross-impacts. The outbreak of financial crises not only makes a country suffer great losses, but also brings about significant side effects on global financial markets. Financial risks appear a strong contagion characteristic, which may lead to systemic financial risk ( Martínez-Jaramillo et al., 2010 ; De Bandt & Hartmann, 2000 ). However, without high correlation among financial markets and institutions, it is hard for a separate event to evolve into overall systemic risk in a short time ( Patro et al., 2013 ). With the increase of financial innovation and economic globalization, the co-movement and interaction effects of financial markets receive more and more attentions from the financial supervisors and researchers.
There are numbers of literatures that have discussed the co-movement and interaction effects among financial markets. These studies can be classified into two aspects. On one hand, there are studies on the cross-border co-movement effect, especially across national stock markets. Aslanidis et al. (2009) investigate co-movement between the US and UK stock returns by time-varying correlations. Allen et al. (2013) examine the spillovers of stock markets from China to Australia, Hong Kong, Singapore, Japan and USA as their trading partners. Cipollini et al. (2015) make research on the short-run co-movements among the US and European countries before and after crises. On the other hand, based on the volatility spillover effect, many researchers have focused on the co-movement between two sub-markets or indicators. For example, Dean et al. (2010) focus on interaction between the equity and bond markets in Australia. Chkili & Nguyen (2014) employ the data from Brazil, Russia, India, China, South Africa and concentrate on the co-movement of exchange rates and stock market returns. Teterin et al. (2016) explore the relationship between oil prices and securities market.
Generally speaking, by means of plenty methods, researchers have reached a consensus about co-movement effect of countries and financial factors. However, little research investigates the interaction relationship among the main financial markets within a country. Therefore, from the perspective of wholeness and systematicness, this paper explores the co-movements and interactions across the main financial markets, such as the monetary, foreign exchange and stock markets, on the basis of the volatility spillover effect and dynamic correlation by using Chinese data.
The rest of the paper is organized as follows. Section 2 analyzes the volatility spillover effect among the monetary, foreign exchange and stock markets based on the ICA-EGARCH-M model. Section 3 further makes research on the dynamic relationship variation process of financial markets with dynamic correlation coefficients from the AG-DCC-MGARCH model. Section 4 concludes the paper.
2. Volatility Spillover Effect
The co-movement and interaction effects of financial markets can be investigated by volatility spillover effect, which represents fluctuation transmitting from one financial market to the others. The previous research on the volatility spillover effect is usually carried out with the multivariate Generalized Auto Regressive Conditional Heteroskedasticity (GARCH) model. In this paper, we employ the Independent Component Analysis (ICA) method to extract independent components as exogenous variables in EGARCH-m volatility equation and investigate the volatility spillover effect based on the coefficients of independent components. The ICA method is a kind of signal separation technology and it can overcome the problems of multicollinearity by generating independent components.
2.1. ICA-EGARCH-M Model
Suppose that there is a time series matrix U. If U = AS and matrix S is an independent component matrix, we regard matrix A as a mix matrix of U. As shown in Equation (1), through the calculation of inverse matrix W of the mix matrix A, the independent component matrix S can be calculated. Any independent component si,t (i = 1, 2, …, m − 1) contains m − 1 yields’ fluctuations, and they are statistically independent from each other. εm−1,t represents residual error sequence. m is the amount of selected financial markets.
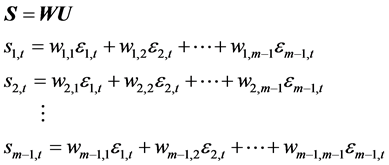 (1)
(1)
In the following, substitute m − 1 independent components as exogenous variables into the other yield’s conditional variance equation as Equation (2), and estimate the model parameters.
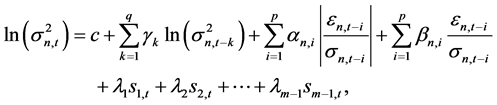 (2)
(2)
where en,t−i is the residual error sequence of market n’s price variable in time t-i, s2 is the variance of corresponding market n’s price variable. When n = 1, it represents the monetary market; When n = 2, it represents the foreign exchange market; When n = 3, it represents the stock market. c is the constant term, p, q is the ARCH and GARCH lag order in conditional variance equations, α and β are asymmetric coefficients of EGARCH model, sm−1,t is independent component, and lm−1 is the coefficient of corresponding independent component. m is the amount of selected financial markets.
2.2. Data and Variable Test
In this section, we introduce our data sources and carry out variable tests. This paper selects daily data of price variables of the monetary market, foreign exchange market and stock market respectively. They are the weighted average Inter- Bank Offer Rate (IBOR), USD-CNY exchange rate (USD-CNY) and Shanghai Composite Index (SHCI). These three variables represent the main financial markets since it is hardly to employ all the sub-markets’ price variables. The data sample is from January 1st 1997 to February 28th 2017. The data source is the Wind database.
First, we calculate the log yields of IBOR, USD-CNY and SHCI respectively. Then we carry out plenty variable tests and make descriptive statistical analysis. According to the Augmented Dickey-Fuller (ADF) tests, the three yield sequences are significantly smooth under 1% level of significance. At the same time, the three yield sequences have conditional heteroscedasticity by Q2(1) statistics, so that the data can be applied into the GARCH model.
2.3. Parameter Estimation of ICA-EGARCH-M Model
First of all, we obtain the residual error sequences by constructing three yield sequences’ mean equations respectively. The residual error sequences consist of the time series matrix U. Then, we employ the ICA method to generate independent components. Using the Rapid Fixed Point Algorithm (FastICA), put forward by Hyvarinen (1999) , to extract independent components from two residual error sequences, we obtain the inverse matrix W. According to the weights of residual error sequences in inverse matrixes, we regard the financial markets’ price variables corresponding to bigger weighted residual error sequences as the represented indicators of corresponding independent components.
As shown in Table 1, in the conditional variance equation of IBOR, λ1 repre- sents the coefficient of independent component of SHCI, λ2 represents the coefficient of independent component of USD-CNY. In the equation of USD-CNY, λ1 represents the coefficient of independent component of IBOR, λ2 represents the coefficient of independent component of SHCI. In the equation of SHCI, λ1 represents the coefficient of independent component of USD-CNY, λ2 represents the coefficient of independent component of IBOR.
The estimation results are listed in Table 2. If the coefficients of independent component are remarkable, we can deduct that the market represented by the independent component has the volatility spillover effect to the yield sequence’s corresponding market.
Table 1. Independent component weights and represented markets.
From the estimation results of Table 2, it is notable that the IBOR (monetary market), USD-CNY (foreign exchange market) and SHCI (stock market) have significant volatility spillover effects with each other. However, there is obvious difference in the volatility spillover effects’ significance levels. Specifically, both the IBOR (monetary market) and the USD-CNY (foreign exchange market) have negative volatility spillover effects on each other, under the significance level of 1%. Moreover, the IBOR (monetary market) has negative volatility spillover effect on the SHCI (stock market) with significance at 1% level, while the SHCI (stock market) has negative volatility spillover effect on the IBOR (monetary market) with significance level of 10%. For comparison, the spillover effects between the stock and foreign exchange markets are insignificant.
2.4. Multi-Market Co-Movements and Interactions
From the above analysis, we can conclude that in addition to the effects between foreign exchange market and stock market, the other markets have significant bidirectional volatility spillover effects. The difference in significant levels reflects asymmetric spillover characteristic. Therefore, we can synthesize the interaction effects among the three major financial sub-markets as shown in Figure 1.
Table 2. Conditional variance equation estimation results.
Note: The superscripts ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels respectively.
Figure 1. Interactions among financial markets.
In the reality, financial markets’ interaction and co-movement effects are obvious. For example, if the central bank raises the benchmark interest rate, that would be a bad news towards national stock markets and the stock indices may drop straight after. This phenomenon is consistent with the result that the IBOR (monetary market) has negative volatility spillover effect on the SHCI (stock market) with significance level of 1%. Also, it can be explained by the theory of Gordon dividend growth model. In addition to this, usually when the interest rate is altered in the monetary market, the foreign exchange rate may also be affected. This phenomenon is consistent with the result that IBOR (monetary market) has negative volatility spillover effect towards the USD-CNY (foreign exchange market) under the significance level of 1%. Similarly, the interest rate parity theory can interpret this realistic phenomena and empirical results.
3. Dynamic Correlation
The above research focuses on the co-movement and interaction effects across the monetary, foreign exchange and stock markets from the volatility spillover effect perspective. These volatility spillover effects are static examination without reflecting dynamic evolution process of relationship among financial markets. In the following section, we make further research on the dynamic correlation of the monetary, foreign exchange and stock markets by employing the Asymmetric Generalized Dynamic Conditional Correlation EGARCH (AG- DCC-EGARCH) model.
3.1. AG-DCC-MGARCH model
The AG-DCC-MGARCH model is proposed by Cappiello et al. (2006) , who has considered the asymmetric shock on the correlation based on the DCC- MGARCH model. The model can be divided into two phases estimation: The first stage is the estimation of single variable respectively by using univariate GARCH; The second phase is the estimation of correlation and parameters of AG-DCC with the maximum likelihood method. We propose that there are m markets. The yields obey zero mean value and their covariance matrixes Ht obey conditional multivariate normal distribution.
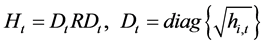 (3)
(3)
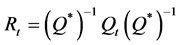 (4)
(4)
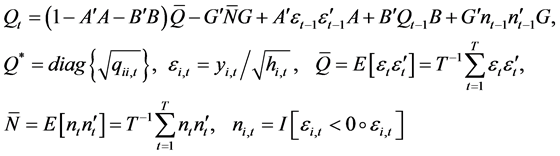 (5)
(5)
In Equations (3)-(5), Dt is the diagonal matrix of condition standard deviation  from the univariate GRACH model, Rt is the time-varying correlation matrix. Q* is the diagonal matrix of
from the univariate GRACH model, Rt is the time-varying correlation matrix. Q* is the diagonal matrix of 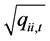 from the matrix Q, A, B, G is the parameter matrix, et is the standardized residuals,
from the matrix Q, A, B, G is the parameter matrix, et is the standardized residuals, 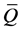 is the unconditional correlation coefficient matrix. I[×] is the indicative function, when et < 0, I[×] equals 1. Otherwise it’s going to be 0. ◦ is the Hadamard Product,
is the unconditional correlation coefficient matrix. I[×] is the indicative function, when et < 0, I[×] equals 1. Otherwise it’s going to be 0. ◦ is the Hadamard Product, 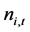 represents the effects of non-symmetrical shocks on conditional correlation. When
represents the effects of non-symmetrical shocks on conditional correlation. When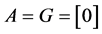 , the AG-DCC model equals Constant Conditional Correlation (CCC) model; when G = [0],
, the AG-DCC model equals Constant Conditional Correlation (CCC) model; when G = [0], 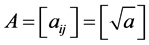 ,
, 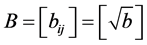 , the AG-DCC model equals DCC model. i, j represent different markets’ price variables.
, the AG-DCC model equals DCC model. i, j represent different markets’ price variables.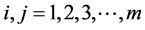 , I ≠ j. Through the above steps, dynamic correlations of market i and market j are calculated as Equation (6).
, I ≠ j. Through the above steps, dynamic correlations of market i and market j are calculated as Equation (6).
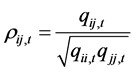 (6)
(6)
3.2. Dynamic Correlation of Financial Markets
Now we use the AG-DCC-MGARCH model to calculate the dynamic correlation coefficients of money market, foreign exchange market and stock market, and investigate the multi-market dynamic evolution process of relationship. The data of IBOR, USD-CNY and SHCI are substituted into AG-DCC-MGARCH model and we can obtain three dynamic correlation coefficients, as shown in Figure 2.
The Figure 2 intuitively demonstrates the dynamic relation between financial markets. From the Figure 2(a), it is clearly that the dynamic correlation coefficient between SCHI (stock market) and USD-CNY (foreign exchange market) fluctuates around zero with mean value of 0.019 and standard variance of 0.116. In addition, from the Figure 2(b), the dynamic correlation coefficient between IBOR (monetary market) and USD-CNY (foreign exchange market) rises and falls under zero with mean value of −0.037 and standard variance of 0.101. Moreover, from the Figure 2(c), the dynamic correlation coefficient between SCHI (stock market) and IBOR (monetary market) waves around zero with mean value of −0.017 and standard variance of 0.114. These results’ plus-minus signs are consistent with the results in previous volatility spillover effects analysis.
From the above analysis, we can find out that the dynamic correlation coefficients of financial markets vary all the time along with the market operation and risk evolution. In other words, financial markets make up a complex and dynamic transforming network. The volatility spillover effects can explore the integral co-movement and interaction effects, while the dynamic correlation is able to directly reflect the dynamic evolution process of relationship among financial markets. These two viewpoints are complementary and both approaches are of interest.
4. Conclusion
This paper makes research on the issue of co-movements and interactions across the China’s monetary, foreign exchange and stock markets. We utilize the
Figure 2. Dynamic correlations of financial markets. (a) Dynamic correlation between SCHI and USD-CNY; (b) Dynamic correlation between IBOR and USD-CNY; (c) Dynamic correlation between SCHI and IBOR.
Notes: In Figure 2 the full line represents dynamic correlation coefficients and the dashed line represents the mean values.
ICA-EGARCH-M model for the volatility spillover effect analysis, as well as employing the AG-DCC-MGARCH model for dynamic correlation calculation. These two approaches are complementary since the volatility spillover effect focuses on the integral but static co-movement and interaction effects, while the dynamic correlation concentrates on the direct reflection of dynamic evolution process of relationship among financial markets. Our results certified the co- movement and interaction effects among the monetary, foreign exchange and stock markets from both static and dynamic point of views.
The co-movement and interaction of financial markets are the basis and precondition of financial risk contagion. Since risk contagion effect is the core of systemic risk, during crises period, the cross-market co-movement effect is enhanced and developed into risk contagion that may lead to systemic risk. In the process of financial market development, the government and financial regulators need to equilibrate the relationship between market co-movement and risk contagion. On the one hand, it is necessary to avoid neglecting the prevention of risk contagion when promoting the market development and strengthening the linkage of financial markets. On the other hand, avoid artificially cutting off the cross-market communication and exchanges for risk contagion prevention.
Acknowledgements
This study is supported by the Science and Technology Planning Project of Guangdong Province (No.2016A020222003) and the Oversea Study Program of Guangzhou Elite Project (JY201517).
Cite this paper
Zhao, X. J., & Zhang, H. (2017). Co-Movement and Interaction Effects across the Monetary, Foreign Exchange and Stock Markets: Evidence from China. Journal of Financial Risk Management, 6, 247-255. https://doi.org/10.4236/jfrm.2017.63018
References
- 1. Allen, D. E., Amram, R., & McAleer, M. (2013). Volatility Spillovers from the Chinese Stock Market to Economic Neighbours. Mathematics and Computers in Simulation, 94, 238-257. [Paper reference 1]
- 2. Aslanidis, N., Osborn, D. R., & Sensier, M. (2009). Co-Movements between US and UK Stock Prices: The Role of Time-Varying Conditional Correlations. International Journal of Finance & Economics, 15, 366-380.
https://doi.org/10.1002/ijfe.402 [Paper reference 1] - 3. Cappiello, L., Engle, R. F., & Sheppard, K. K. (2006). Asymmetric Dynamics in the Correlations of Global Equity and Bond Returns. Journal of Financial Econometrics, 4, 537-572.
https://doi.org/10.1093/jjfinec/nbl005 [Paper reference 1] - 4. Chkili, W., & Nguyen, D. K. (2014). Exchange Rate Movements and Stock Market Returns in a Regime-Switching Environment: Evidence for BRICS Countries. Research in International Business and Finance, 31, 46-56. [Paper reference 1]
- 5. Cipollini, A., Cascio, I. L., & Muzzioli, S. (2015). Volatility Co-Movements: A Time-Scale Decomposition Analysis. Journal of Empirical Finance, 34, 34-44. [Paper reference 1]
- 6. Dean, W. G., Faff, R. W., & Loudon, G. F. (2010). Asymmetry in Return and Volatility Spillover between Equity and Bond Markets in Australia. Pacific-Basin Finance Journal, 18, 272-289. [Paper reference 1]
- 7. De Bandt, O., & Hartmann, P. (2000). Systemic Risk A Survey. European Central Bank Working Paper Series, No.35. Frankfurt: European Central Bank. [Paper reference 1]
- 8. Hyvarinen, A. (1999). Fast and Robust Fixed-Point Algorithms for Independent Component Analysis. IEEE Transactions on Neural Networks, 10, 626-634.
https://doi.org/10.1109/72.761722 [Paper reference 1] - 9. Martínez-Jaramillo, S., Pérez, O. P., Embriz, F. A., & Dey, F. L. G. (2010). Systemic Risk, Financial Contagion and Financial Fragility. Journal of Economic Dynamics and Control, 34, 2358-2374. [Paper reference 1]
- 10. Patro, D. K., Qi, M., & Sun, X. (2013). A Simple Indicator of Systemic Risk. Journal of Financial Stability, 9, 105-116. [Paper reference 1]
- 11. Teterin, P., Brooks, R., & Enders, W. (2016). Smooth Volatility Shifts and Spillovers in U.S. Crude Oil and Corn Futures Markets. Journal of Empirical Finance, 38, 22-36. [Paper reference 1]




