Journal of Financial Risk Management
Vol.04 No.02(2015), Article ID:56606,9 pages
10.4236/jfrm.2015.42007
A Comparative Study of Mean-Variance and Mean Gini Portfolio Selection Using VaR and CVaR
Jamal Agouram*, Ghizlane Lakhnati
National School of Applied Sciences (ENSA), Agadir, Morocco
Email: *jamal.agouram@edu.uiz.ac.ma, g.lakhnati@uiz.ac.ma
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 February 2015; accepted 22 May 2015; published 25 May 2015
ABSTRACT
This paper focuses on two methods for optimum market portfolio selection. We compare the Mean-Variance method with the Mean-Gini method using MADEX data from turbulent market periods in 2011, 2012 and 2013. We compare both strategies with reference to value at-risk (VaR) and conditional value-at-risk (CVaR) measures during periods of financial crisis. The results show that both strategies are profitable for investors. We consider the Mean-Gini strategy to be the more secure strategy during periods of market instability.
Keywords:
Conditional Value-at-Risk, Mean-Gini, Mean-Variance, Portfolio Selection, Value-at-Risk

1. Introduction
During a financial crisis, it is of critical importance to implement the best investment strategy possible to match an investor’s preferences in terms of risk and returns. Several studies have evaluated and compared different pairs of portfolio strategies in terms of their return and risk characteristics. The Mean-Variance (MV) theory, suggested by Markowitz (1952a, 1952b) , marked the starting point of the development of modern finance theory. The theory is based on the presumption that distribution of portfolio returns is normal and can be successfully described by two moments: mean and variance. However, the application of MV optimisation is questionable because it does not consider the direction of price movement; optimising the variance can prevent an investor from losses in the same manner as from gains. Roll (1977, 1978, and 1979) was the first to point out other weaknesses of the theory. This evidence forced several theorists to search for other, more appropriate models to determine the best possible return/risk relationship. For instance, Markowitz (1959) , Fishburn (1977), Bawa (1977) proposed the use of the mean-lower partial moment approach, Yitzhaki (1982) , Shalit and Yitzhaki (1984) proposed the use of the Mean- Gini (MG) portfolio selection model, and Konno and Yamazaki (1991) proposed the use of the Mean-Absolute Deviation (MAD) approach.
The restrictive character of variance as a risk parameter, led us to choose the MG strategy as an alternative to the MV strategy. The MG strategy uses Gini as a parameter of risk instead of variance. The concept of MG was proposed by Shalit and Yitzhaki (1984) as an alternative method to the MV approach proposed by Markowitz (1952) because it can outstrip normal assumptions of return distribution and utility function quadratics. Yitzhaki (1982) has shown that the Gini coefficient satisfies the second degree stochastic dominance, which makes the MG model compatible with the theory of expected utility.
This study provides a comprehensive statistical analysis of four strategies: the MV strategy versus the MG strategy and the Minimum Variance (Min-V) versus the Minimum Gini (Min-G) strategy.
Following Agouram and Lakhnati (2015) , in order to verify the reliability of these strategies, we used quasi- analytic VaR, computing and only portfolio VaR, with any additional information pertaining to important characteristics of financial asset returns (i.e. their volatility, clustering and non-normal distributions). We considered the following aspects in forecasting VaR for each strategy.
Firstly, we used the GARCH (1.1) model to explore the sensitivity of VaR to return distribution characteristics assuming that portfolio return follows the classical normal distribution and the student-t distribution.
Secondly, we numerically computed VaR using the Cornish-Fisher expansion and the Johnson SU approximation to forecast portfolio VaR, to take into account fat tails and skewness on forecasting VaR.
Finally, we utilised CVaR to compare the two pairs of strategies because the outcomes are similar and CVaR can better capture the tail risk. This risk measure follows directly from the value-at-risk.
This paper is organised as follows: Firstly, we present the framework of the four models: MV, MG, Min-V and Min-G. Secondly, we provide a comprehensive explanation of the data and methodology used, and define the key terms. Finally, we apply the GARCH (1.1) model with the Cornish-Fisher expansion and the Johnson SU approximation to forecast VaR and CVaR.
2. Materials
2.1. Mean-Variance
A portfolio is defined to be a list of weights 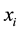 for assets
for assets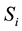 ,
, 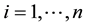 , which represent the amount of capital to be invested in each asset. We assume that one unit of capital is available and require that capital to be fully invested. Thus we must respect the constraint that
, which represent the amount of capital to be invested in each asset. We assume that one unit of capital is available and require that capital to be fully invested. Thus we must respect the constraint that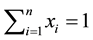 . The return of portfolio
. The return of portfolio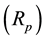 , obtained by
, obtained by 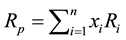 (
(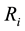 is the return of asset
is the return of asset 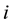 per period).
per period).
In the traditional Markowitz portfolio optimisation, the objective is to find a portfolio which has minimal variance for a given expected return. More precisely, one seeks such that:
Min 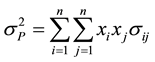
Subject to:
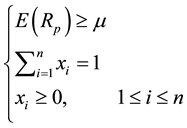 (1)
(1)
where 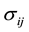 is the covariance between the returns of
is the covariance between the returns of , and
, and 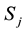 and
and 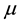 is the minimal rate of return required by an investor.
is the minimal rate of return required by an investor.
The Minimum Variance analysis consists of constructing a portfolio without a given expected return; the optimisation program is presented mathematically as follows:
Min 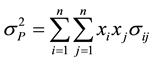
Subject to:
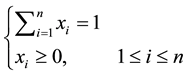 (2)
(2)
2.2. MG Analysis
The MG approach is consistent with stochastic dominance for decisions about risk and is ideal for portfolio analysis for a variety of financial assets. The MG analysis introduced by Shalit and Yitzhaki (1984) defines the Gini coefficient as an index of variability of a variable random.
The approach used by these authors assumes that the cumulative distribution corresponding to the observation with rank 

Specifically, Dorfman (1979) and Shalit and Yitzhaki (1984) retain as a measure of the Gini coefficient:
where 

The MG mathematical model is presented as follows:
Minimize:
Subject to:

where 





The Minimum Gini as the Minimum Variance analysis. The optimisation program is presented mathematically as follows:
Minimize:
Subject to:

2.3. VaR
Value-at-Risk is a measure of risk. It represents the maximum loss of the portfolio with a certain confidence probability





In the case of normal distribution, the parametric VaR is calculated by:
where

Zangari (1996) , Favre and Galeano (2002) provide a modified VaR calculation that takes the higher moments of non-normal distributions (skewness and kurtosis) into account through the use of the Cornish-Fisher expansion.
where 



The Johnson SU distribution we use here differs from the Cornish-Fisher approach. It transforms a random variable 

where 




The Johnson SU value-at-risk is obtained by:
2.4. CVaR
CVaR, also known as Expected Shortfall, can be defined as the expectation of the loss when the loss exceeds VaR. Since VaR measures the value that separates the 


2.5. GARCH (1.1) Model
In this study, volatility was estimated by applying a GARCH (1.1) model to each portfolio. This is a familiar model in econometrics; see
Shephard (1996)
. If 



where 


3. Methods
This paper focuses on the MADEX. We propose to build a portfolio composed only of assets from the MADEX over a period of national and global financial crisis spanning 01/01/2011 to 10/01/2014. Our dataset consists of a daily series of returns, which served as a benchmark for comparing relative profitability of strategies MV and MG. The six risky assets selected are those most sensitive during the examined period: Addoha, Atlanta, BCP, Delta Holding, Managem and Maroc Telecom.
This study begins with an analysis of the characteristics of six selected assets that allows the construction of a portfolio using the MV strategy, the MG strategy, the Min-V strategy and Min-G strategy. This analysis determines the weights of the six assets. Descriptive statistics are presented in Table 1.
The strong results for the normality test (Jarque-Bera) for each stock, led us to reject the null hypothesis of the normality test at 99% confidence level. These results indicate a well-known property of financial data series: returns are usually not normally distributed. In addition, skewness and kurtosis, other properties of risky assets, have been discovered in our data series. Since both properties are apparent in our data, we assume that using the Mean- Gini strategy should provide the best portfolio due to the fact that the Gini strategy exceeds normal return distribution assumptions. Based on these results, we assume that in the context of our data, MG strategy must produce better results than the MV strategy.
After the application of optimisation programs of the MV strategy, the MG strategy, the Minimum Variance strategy (Min-V) and the Minimum Gini strategy (Min-G), we obtained their optimum portfolios in Table 2 and Table 3 presents summary statistics of optimal portfolios obtained by the resolution of optimization programs.
Table 1. Descriptive statistics.
Table 2. Percentage of stocks in optimal portfolios.
Table 3. Summary statistics of optimal portfolios.
Return series for optimal portfolios are plotted in Figure 1. Plots demonstrate that the return series are extremely unstable.
In order to make the comparison of the two strategies clearer, we used quasi-analytic VaR and CVaR methods using the GARCH (1.1) model, because the variance is not homoscedastic as the ARCH test result proves. This was done in order to take into account those specific characteristics apparent in our data. In order to move away from a normal distribution framework for the prediction of VaR and CVaR, we used the Cornish-Fisher expansion and the Johnson SU approximation.
Table 4 presents the different tests of stationary. We accept the alternative hypothesis that the series of returns of the four portfolios are stationary and the result of the ARCH test leads us to reject the null hypothesis. Therefore, it is assumed that the residual variance is not homoscedastic. The prediction the quasi-analytic VaR and CVaR of portfolios will be made on a GARCH (1; 1) model.
4. Results
4.1. Estimating Parameters
The results of the goodness-of-fit tests for different models ARMA/GARCH show clearly that a combination of AR (1)-GARCH (1.1) and Gaussian residuals and student-t residuals are the appropriate models, from a statistical
Figure 1. Evolution of four portfolios.
Table 4. Unit root tests of the series of returns.
point of view, for portfolios in times of market turbulence. Table 5 and Table 6 present parameters of GARCH (1.1) Model with Normal Distribution and Student-t Distribution.
4.2. Back-Testing VaR Estimates
We evaluated the accuracy of the proposed VaR estimates over a 250 day period using the now standard coverage tests of
Christoffersen (1998)
. We combined the GARCH (1.1) model with the approximation method. The Cornish-Fisher expansion, and the Johnson SU approximation derive the VaR estimates for each portfolio where
In finance literature tells us that there are two fundamental test procedures used to compare the performances of VaR: Unconditional and Conditional. We make use of Kupiec’s (1995) Test to evaluate GARCH specifications for unconditional coverage, and the Christoffersen Test to embrace both unconditional coverage and the independence of violations. The Kupiec Test and Christoffersen Test results for the portfolios are reported in Tables 7-10.
Table 5. Estimating parameters of GARCH (1.1) model with normal distribution.
Table 6. Estimating parameters of GARCH (1.1) model with student-t distribution.
Table 7. Unconditional coverage and conditional coverage of VaR GARCH (1.1) model with normal distribution.
Finally, we utilised CVaR to compare the two pairs of strategies because the outcomes are similar and CVaR can better capture the tail risk. Results are reported in Tables 11-14.
5. Discussion
This paper discusses and compares analytical results obtained with MV, MG, the Min-V and the Min-G strategies on the Moroccan financial market (MADEX) during periods of market instability, and demonstrates, empirically, that quasi-analytic GARCH VaR forecasts can be accurately constructed using analytic formulae for higher moments of aggregated GARCH returns by using Cornish-Fisher expansion and the Johnson SU distribution.
Results show that the composition of two pairs of strategies: MV versus MG and Min-versus Min-G strategy are similar but not identical for that we have very close results in the VaR which is not convincing to compare the two strategies. The judgment is conclusive when considering the CVaR because the MG strategy has lower
Table 8. Unconditional coverage and CONDITIONAL coverage of VaR GARCH (1.1) model with student-t distribution.
Table 9. Unconditional coverage and conditional coverage of VaR GARCH (1.1) model with normal distribution.
Table 10. Unconditional coverage and conditional coverage of VaR GARCH (1.1) model with student-t distribution.
Table 11. CVaR GARCH (1.1) model with normal distribution.
**Represent the lower CVaR of both strategies.
Table 12. CVaR (1.1) model with student-t distribution.
**Represent the lower CVaR of both strategies.
Table 13. CVaR GARCH (1.1) model with normal distribution.
**Represent the lower CVaR of both strategies.
Table 14. CVaR (1.1) Model with student-t distribution.
**Represent the lower CVaR of both strategies.
*Corresponding author.
In view of these results, we conclude that the MG strategy outperforms the MV strategy in our real-world examples taken from the Moroccan Financial Market. This is due to the characteristics of the financial assets that do not follow a normal distribution and the unstable nature of the variance in time.
There was great accuracy for all significance levels (10%, 5% and 1%), when we considered for GARCH VaR forecasting. Our results are even more remarkable when we consider that the analysis is entirely out-of- sample and that the testing period (2011-2014) covers several prolonged periods of excessively turbulent financial market activity.
References
- Agouram, J., & Lakhnati, G. (2015). Mean-Gini Portfolio Selection: Forecasting VaR Using GARCH Models in Moroccan Financial Market. Journal of Economics and International Finance, 7, 51-58.
- Christoffersen, P. F. (1998). Evaluating Interval Forecasts. International Economic Review, 39, 841-862. http://dx.doi.org/10.2307/2527341
- Dorfman, R. (1979). A Formula for the Gini Coefficient. Review of Economics and Statistics, 61, 146-149. http://dx.doi.org/10.2307/1924845
- Favre, L., & Galeano, J. A. (2002). Mean-Modified Value-at-Risk Optimization with Hedge Funds. Journal of Alternative Investments, 5, 2-21. http://dx.doi.org/10.3905/jai.2002.319052
- Kupiec, P. (1995). Technique for Verifying the Accuracy of Risk Measurement Models. Journal of Derivatives, 2, 173-184. http://dx.doi.org/10.3905/jod.1995.407942
- Markowitz, H. (1952a). Porfolio Selection. Journal of Finance, 7, 77-91.
- Markowitz, H. (1952b). The Utility of Wealth. The Journal of Political Economy (Cowles Foundation Paper 57), LX (2), 151-158.
- Markowitz, H. (1959). Portfolio Selection: Efficient Diversification of Investments. New York: Wiley.
- Shalit, H., & Yitzhaki, S. (1984) Mean-Gini, Portfolio Theory, and the Pricing of Risky Asset. Journal of Finance, 39, 1449- 1468. http://dx.doi.org/10.1111/j.1540-6261.1984.tb04917.x
- Shephard, N. (1996). Statistical Aspects of ARCH and Stochastic Volatility. Monographs on Statistics and Applied Probability, 65, 1-68.
- Yitzhaki, S. (1982). Stochastic Dominance, Mean-Variance, and Gini’s Mean Difference. American Economic Review, 2, 178-185.
- Zangari, P. (1996). A VaR Methodology for Portfolios That Include Options. RiskMetrics Monitor, JP Mogran-Reuters, First Quarter, 4-12.
NOTES
*Corresponding author.



















