Journal of Financial Risk Management
Vol.3 No.2(2014), Article
ID:46721,11
pages
DOI:10.4236/jfrm.2014.32004
Is the Distribution of Returns Symmetric?
Is the Distribution of Returns Symmetric?
—Empirical Evidence from Agricultural Futures Market of China
Peng Wang1,2*, Tao Xiong3
1Institute of Chinese Financial Studies, Southwest University of Finance and Economics, Chengdu, China
2Collaborative Innovation Center of Financial Security, Chengdu, China
3School of Finance, Southwest University of Finance and Economics, Chengdu, China
Email: *wangp@swufe.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 April 2014; revised 5 May 2014; accepted 2 June 2014
Abstract
The presence of asymmetry in the distribution of financial returns is not only an important factor should be considered in the process of optimal portfolio allocation, but also one of the variables having close relationship with the recognition and measurement of financial risk. This paper adopts a method based on bootstrap to measure asymmetry in the distribution of financial returns, as proposed by Lisi (2007). Results of asymmetry test on the distribution of four representative price index series coming from agricultural futures market in China are presented, and the four indexes are hard wheat index, cotton index, sugar index and soybean oil index. The results indicate that, except for the distribution of soybean oil index return which has an evident asymmetry characteristic, the other three ones all can be considered symmetric at a high confidence level. This paper contributes to asymmetry evaluation in the marginal distribution of financial returns, as well as the study of distribution characteristics in agricultural futures index returns of China, in the way of providing new empirical evidence.
Keywords:Agricultural Product Futures Market, Asymmetry, Bootstrap

1. Introduction
Agricultural futures market is an important part of modern financial system, whose functions of producing guiding, hedging, and market stabilization have gained wide attention from governments, enterprises and institutions, and therefore, it has been growing and developing since its emergence. Moreover, the growth and development is largely drove by the rapid development of Chinese market. By the end of 2012, dozens of agricultural futures contracts of 12 major categories have been traded in China, which basically cover major kinds of agricultural products closely related to national economy and the people’s livelihood. As the perfection of Lisied varieties, Chinese agricultural futures market has maintained a high-speed growth in the volume of sales in recent years. According to the Futures Industry Association of America, China has already owned the biggest agricultural futures trading volume in the world in 2008. During the next two years, trading volume of Chinese agricultural futures experienced an explosive growing.
In recent years, what accompanies the rapid development of Chinese agricultural futures market are the valuable researches conducted by Chinese scholars in many aspects of agricultural futures market such as properties and determinants of price volatility. Most of the existing researches focus on either the relationship between the price of agricultural futures and macro variables, or price volatility in the agricultural futures market. For instance, Tang Yanwei et al. (2005) studied the long-range correlation in price volatility in Chinese agricultural futures market using the method of modified R/S; Wang Jun, Zhang Zongcheng (2006) established a vector autoregressive model of Chinese agricultural futures; Zhang Shuzhong et al. (2006) gave a research on the relationship between the price index of agricultural futures and the CPI; also, Shi Limin et al. (2009) analyzed the empirical relationship between the exchange rate and the agricultural futures prices; in addition, Yi Rong et al. (2010) examined the basis of agricultural futures based on the expectation theory. These important findings have contributed a lot to our understanding of the empirical volatility properties and the risk conditions in Chinese agricultural futures market. However, there is no specialized and systematic research on the asymmetry in the distribution of Chinese agricultural futures price (return), to the best of the authors’ knowledge.
In fact, the asymmetry in the distribution of financial returns is not only an important factor should be considered in the process of optimal portfolio allocation, but also one of the variables having close relationship with the recognition and measurement of financial risk. As early as 1970, Samuelson (1970) has pointed out that if the return distributions are asymmetric, the expected return, volatility and asymmetry must be all considered when allocate an optimal portfolio. This point has been confirmed by Harvey et al. (2010) in their recent studies, who found that a three-factor model considering the factor of asymmetry can obtain higher expected utility than the conventional CAPM. Rosenberg and Schuermann (2006) also suggest that if return distribution is asymmetric, the consideration of it in existing tools of risk measure (such as VaR) will help to improve the accuracy of risk estimation. In addition, the asymmetry in return distribution also affects the accuracy of the derivatives pricing greatly. For instance, in classic Black-Scholes option pricing model, asset price is assumed to follow the Geometric Brownian Motion, so (continuously compounded) returns can be regarded as following normal distribution at any point in time. However, in practice this model has been proved to usually misprice the in-themoney call option and out-of-the-money put option. Some scholars indicate, this is mainly due to the improper assumption on the actual statistical properties of returns such as symmetry in classic Black-Scholes model. Furthermore, modified pricing model containing the asymmetry variable can achieve better accuracy than the classic model (Christoffersen et al., 2006).
Because both the theoretical and practical significance attributed to the research on asymmetry in financial return series, in recent years, this kind of research has gradually rise, and gets a number of valuable achievements. However, it must be pointed out that in present there are still many controversial issues in this important area, one of which is the fundamental problem that which method should be adopted to measure asymmetry in return distribution1.
In conventional way of study, we usually use coefficient of skewness defined as the standardized third central moment of a random variable to measure the asymmetry. However, when use coefficient of skewness to test asymmetry, not only the independence of price volatility but also the important assumption of normal distribution determines the accuracy and effectiveness of the conclusion (Kendall & Stuart, 1969). In other words, conclusion of asymmetry test based on standardized third central moment is highly questionable when the return is not independent of each other or does not follow normal distribution. Unfortunately, many rigorous empirical studies already showed that though there is no significant auto-correlation in the original series of financial return, there is strongly significant positive auto-correlation in the the squared (or absolute) data, indicating that price changes (returns) at various points in time are not independent (Engle, 1982; Christofferson, 2003; Terasvirta & Zhao, 2011). Moreover, hypothesis of normal distribution is strongly rejected when sample on the commonly used frequency (e.g., daily or weekly) (Karoglou, 2009; Khalifa et al., 2011).
In order to solve the problem that the basic assumptions do not tally with the actual properties of financial data in conventional asymmetry test, Lisi (2007) proposed a method based on bootstrap to test asymmetry in financial return series. This method can be applied to dependent and non-normal financial return data, what’s more, a Monte Carlo experiment showed that test results of the method are highly consistent with the data generation mechanism when apply it to time series generated by different mechanism, namely, the results are very accurate and reliable.
It should be pointed out that, although asymmetry test has been conducted in descriptive statistics part in many empirical research literatures studying the properties of price volatility in Chinese agricultural futures market, the test methods used in these papers are mostly confined to the conventional way, namely test based on coefficient of skewness (Tang Yanwei et al., 2005; Wang Jun & Zhang Zongcheng, 2006; Zhang Shuzhong et al., 2006; Shi Limin et al., 2009). The bootstrap method is more suitable for the real financial data, but there is still no paper adopting it to in-depth research of asymmetry in distribution of Chinese agricultural futures return, to the authors’ knowledge.
Within this context, the aim as well as innovation of this paper is to evaluate the presence of asymmetry in the distribution of Chinese agricultural futures return, by studying four representative price indexes in the market and by a test method based on bootstrap, so as to provide more accurately and reliably empirical evidence for the question that whether there is significant asymmetry existing in the return distribution of the financial market.
The rest contents are arranged as follows: a explication of four representative price indexes in Chinese agricultural futures market and a tentative exploration of the statistics properties of these price indexes will be in the first part; the second part will expounds the procedures of the test method based on bootstrap we use to examine the asymmetry in financial return series; the third part will put the asymmetric question to a practical test using the bootstrap-based method mentioned above, and then compare the test results to the ones coming from the conventional method of skewness coefficient; the fourth part is a robustness test on the research conclusions; finally are the main conclusions and recommendations for future research.
2. Data
Since the establishment in the 1990s, Chinese agricultural futures market has developed into a complete system including four main series of varieties of agricultural futures, which is grain, cotton, oil and sugar. By the end of 2010, Zhengzhou and Dalian Commodity Exchange have had 12 categories, dozens of varieties of agricultural futures Lisied, that is wheat, corn, cotton, soybeans, sugar, soybean oil, rapeseed oil, palm oil, etc., which are closely related to national economy and the people’s livelihood.
Considering factors such as different roles that different trade categories play in Chinese agricultural system and the trading volume of the futures contracts, we selected hard wheat index, cotton index, sugar index in Zhengzhou Commodity Exchange and soybean oil index in Dalian Commodity Exchange as the study sample, and mark daily closing price of each index as pt. The sample periods of cotton index, sugar index and soybean oil index are from the Lisied dates to December 20, 2010, including about 1500 sample points; and for the hard wheat index, the sample period is from January 4, 2000 to December 20, 2010, including 2653 sample points. All the data comes from Wenhua financial index system.
Define daily return 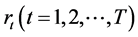 of the indexes as:
of the indexes as:
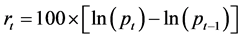 (1)
(1)
Figure 1 depicts the volatility of the four return series of indexes, and Table 1 presents results of descriptive statistics analysis.
The following facts can be drawn from Table 1 and Figure 1:
Firstly, for all the four return series, the high returns and the low returns appear alternately within certain periods, namely there is an obvious volatility clustering effect existing in the returns of Chinese agricultural futures;
Secondly, the return series do not obey normal distribution (at 1% level of significance by J-B test), in addition,
Table 1. Descriptive statistics analysis on the four return series of agricultural futures indexes.
Note: * and † denote significance at 1% and 10% levels, respectively. Kurtosis represents excess kurtosis coefficient and the excess kurtosis coefficient of the normal distribution is 0; J-B is a Jarque-Bera statistic used to test whether a return series obeys the normal distribution; ADF is Augmented Dickey Fuller statistic used to test unit root and the optimal number of lags in it is determined by AIC criterion; Q(n) is Ljung-BoxQ statistic with n lags of the dependent variable.
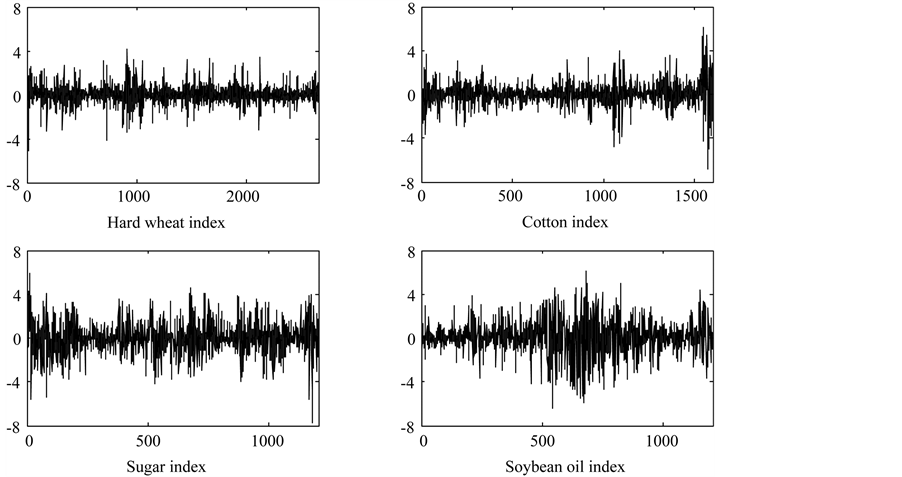
Figure 1. Volatility of the four index returns.
series are generally leptokurtic, fat tailed and skewed (Except return series of cotton index, the rest three ones’ skewness coefficient are significantly less than zero and excess kurtosis coefficient are significantly greater than zero);
Thirdly, ADF test results in Table 1 show that the null hypotheses of a unit root in return series are all rejected significantly, therefore the series are stationary and the further analysis and econometric modeling process are practicable;
In the end, the Ljung-BoxQ statistics in Table 1 shows that, the null hypotheses of no autocorrelation in return series of hard wheat index and cotton index must be rejected in a long time range (10), while for sugar index and soybean oil index the same null hypothesis cannot be rejected.
3. Methodological Issues
In financial econometrics, the dynamic process of return rt of assets is usually assumed to be:
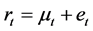 (2)
(2)
where 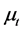 is conditional mean value of return, and the residual
is conditional mean value of return, and the residual 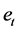 is an uncorrelated (but not necessarily independent or homoscedastic) process.
is an uncorrelated (but not necessarily independent or homoscedastic) process.
Because financial return series often have the property of autocorrelation, many researchers assume the series to obey the autoregressive moving average (ARMA) process in their empirical studies to eliminate the autocorrelation (Mcneil & Frey, 2000; Bali & Theodossiou, 2007; Sabiruzzaman et al., 2010).
After this reasonable handling of the data, the asymmetry test on return rt is equivalent to asymmetry test on the residuals (Lisi, 2007).
As mentioned earlier, majority of the study methods used to test asymmetry in financial return series are the conventional skewness coefficient S, it is:
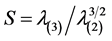 (3)
(3)
where 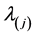 is the jth central moments. According to the relevant statistical theory, the sample’s skewness coefficient calculated from the corresponding sample moments obeys Gaussian asymptotic distribution under the null hypothesis of S = 0, that is:
is the jth central moments. According to the relevant statistical theory, the sample’s skewness coefficient calculated from the corresponding sample moments obeys Gaussian asymptotic distribution under the null hypothesis of S = 0, that is:
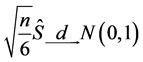 (4)
(4)
However, the existence of the variance of the asymptotic distribution is largely dependent on the validity of the assumption that the data is independent and follows normal distribution. Many researchers have pointed out that the assumption of normality and independence is not in accordance with the real properties of financial series. Some scholars have also studied how the variance of the skewness coefficient changes with the relaxation of the two assumptions (Bera & Premaratne, 2001; Peiro, 2004; Bai & Ng, 2005).
In order to solve the above problem, Lisi (2007) proposed a bootstrap-based asymmetry test method. The robustness test conducted by Monte Carlo simulation shows that, because the bootstrap is adopted to generate the symmetric distributions of actual financial series, the bootstrap-based asymmetry test is not only applicable to uncorrelated time series, but also applicable to autocorrelated and heteroscedastic financial time series after using ARMA to filtering out the autocorrelation. Therefore, compared with the conventional skewness coefficient, the bootstrap-based asymmetry test proposed by Lisi (2007) has a more reasonable theoretical basis and can test asymmetry in financial series more accurately and reliably.
The basic idea of Lisi’s (2007) method is that: the symmetrized version of observed data can be obtained by the bootstrap procedure ignoring that the distribution of observed data is symmetric or not, then critical values at certain confidence levels can be calculated, and by comparing the critical values and skewness coefficient of actual data we can judge whether the distribution is asymmetric. The test procedure is described in the following.
1) Set the hypothesis system as:
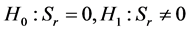 (5)
(5)
2) Given the return series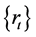 ,
, 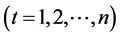 , fit a suitable ARMA (p, q) model if
, fit a suitable ARMA (p, q) model if 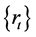 is autocorrelated. Orders p and q can be chosen by AIC criteria. Let et be the series of residuals of the model, i.e.
is autocorrelated. Orders p and q can be chosen by AIC criteria. Let et be the series of residuals of the model, i.e.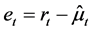 , and then calculate the skewness coefficient
, and then calculate the skewness coefficient 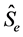 for the series et.
for the series et.
3) Define variable 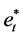 as:
as:
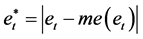 (6)
(6)
where 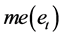 is the median of et.
is the median of et.
4) Define the other variable 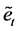 as:
as:
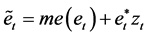 (7)
(7)
where 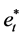 is sampled with replacement from the empirical distribution of e* and zt is a random variable following binomial distribution, namely:
is sampled with replacement from the empirical distribution of e* and zt is a random variable following binomial distribution, namely:
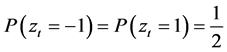 (8)
(8)
The distribution of 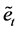 represents a symmetrized version of that of et.
represents a symmetrized version of that of et.
5) Calculate skewness coefficient 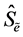 for series
for series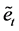 .
.
6) Repeat Steps 4 and 5 M times, so M bootstrap samples 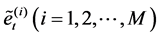 can be generated as well as M corresponding estimates
can be generated as well as M corresponding estimates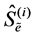 .
.
7) Find quantiles 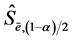 and
and 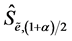 of significance level a from the bootstrap distribution of
of significance level a from the bootstrap distribution of 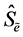 obtained from M bootstrap estimates.
obtained from M bootstrap estimates.
8) Reject 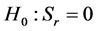 at level a if
at level a if 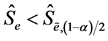 or
or 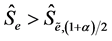 (
(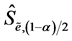 is the left-tail critical value and
is the left-tail critical value and 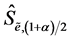 is the right-tail critical value), so the return series rt is asymmetric, and vice versa.
is the right-tail critical value), so the return series rt is asymmetric, and vice versa.
4. Bootstrap-Based Asymmetry Test on Return Series of Agricultural Futures Index
4.1. Autocorrelation Treatment
As mentioned in section 2, the autocorrelation in original series need to be filtered out by ARMA model before conduct the asymmetry test on return series of Chinese agricultural futures index. Meanwhile, test results of Q1(10) statistic in Table 1 shows that series of hard wheat index and cotton index have an obvious property of autocorrelation, while series of sugar index and soybean oil index do not. So series of hard wheat index and cotton index must have some “autocorrelation treatment”.
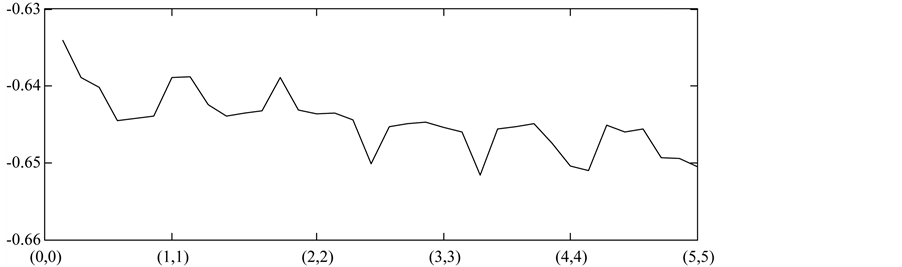
Before use ARMA (p,q) model to fit the distribution of series of hard wheat index and cotton index, the orders p and q need to be chosen by AIC criteria first. Synthetically considering the accuracy and efficiency of the estimation process, we set the range of orders p and q to 0, 1, …, 5. So we have 35 waiting model, namely ARMA (0,1), ARMA (1,0), …, ARMA (5,5). Then WinRATS is used to find out which model minimizes the AIC value. Figure 2 displays how the AIC value changes with the 35 ARMA (p,q) models for hard wheat index and cotton index.
AIC selects an ARMA (3,5) to fit the return series rt of hard wheat index in Figure 2(a), that is:
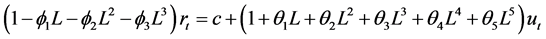 (9)
(9)
where L is the lag operator, c is a constant term.
And AIC selects an ARMA (4,5) to fit the return series rt of cotton index in Figure 2(b), that is:
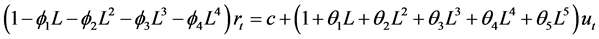 (10)
(10)
 (a)
(a)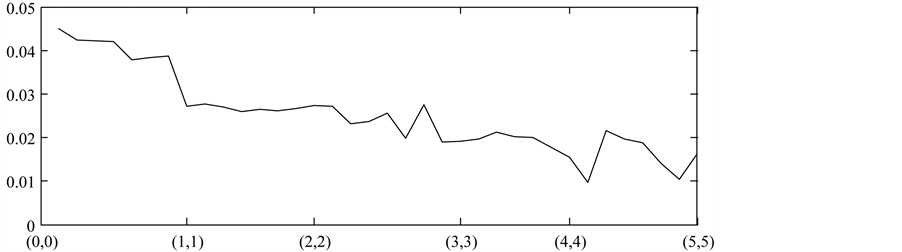 (b)
(b)
Figure 2. (a) AIC value changing with ARMA (p,q) models for hard wheat index; (b) AIC value changing with ARMA (p,q) models for cotton index.
Table 2 reports results of parameter estimation of the models specified before for return series of hard wheat and cotton index and results of model checking.
After the model estimation process, residual series et in Equation (2) can be generated. The outcome of residual diagnostics in the last row of Table 3 indicates that there is already no significant linear dependence in residual series, which suggests that the ARMA models originally specified for return series of hard wheat and cotton index are adequate to capture the features of the data. Because there is no significant autocorrelation in the return series of soybean oil and sugar index, they don’t need to have “autocorrelation treatment”. In the next
Table 2. Results of parameter estimation and model checking.
Note: The upper half of the table shows results of parameter estimation for ARMA models and the lower half shows results of model checking. Bracketed numbers mean the exact significance level (p-value) attached to the test statistic used in parameter significance test. LR represents the value comes from MLE (maximum likelihood estimation) of the models and the last row Q1(10) gives the statistic resulting from a Ljung-Box test with 10 lags on residual series.
Table 3. Results of asymmetry test based on bootstrap and coefficient of skewness.
steps, the return series rt of soybean oil and sugar index would be directly taken as series et to conduct asymmetry tests.
4.2. Empirical Results of Bootstrap-Based Asymmetry Test
After obtain residual series et with no significant autocorrelation, bootstrap-based asymmetry test can be conducted as described in part 2. In order to ensure the robustness of study results, we repeat bootstrap sampling 1000 times, and test asymmetry in the return series at three different significant levels 90%, 95% and 99%.
As mentioned before, test results are based primarily on the empirical distribution obtained by 1000 times’ bootstrap sampling, therefore the empirical distributions are figured in Figure 3 and detailed statistical test results are presented in Table 3. Moreover, Table 3 also reports results of asymmetry test based on coefficient of skewness at different significant levels, to be compared with results of bootstrap-based test.
As can be seen from Figure 3 that the empirical distribution of soybean oil index’s return series is obviously asymmetric and the other three ones seem to be symmetric. Quantitative test results in Table 3 can prove what we see in Figure 3: bootstrap-based asymmetry test results indicate that the null hypotheses that distributions of return series of hard wheat, cotton and sugar index are symmetric respectively cannot be rejected at three different significant level 90%, 95% and 99%, while for soybean oil index the null hypothesis is rejected significantly at the 99% level. That is to say, bootstrap-based asymmetry test has given very clear test conclusions on whether the distributions of return series of the four typical indexes in Chinese agricultural futures market are asymmetric, that is, except that the distribution of return series of soybean oil index is significantly asymmetric, the rest three ones are symmetric.
In addition, from the comparison of test results based on bootstrap and coefficient of skewness above we can find that there are some differences between the test conclusions given by the two different methods. Especially for the case of test on return series of hard wheat and sugar index at significance level 90%, the two asymmetry test methods give two totally opposite results. The bootstrap-based test rejects the null hypothesis of symmetry in hard wheat index’s return series at significance level 90%, while test based on skewness coefficient leads to the opposite conclusion. Similarly, test based on skewness coefficient rejects the null hypothesis that the distribution of sugar index’s return series is symmetric at significance level 90% while bootstrap-based test accepts the null hypothesis at the same significance level.
Furthermore, we find out that the difference between results of the two methods as mentioned above, is essentially due to the different applicable conditions the two asymmetry test methods need to work well. As described in introduction, the correctness and effectiveness of the asymmetry test based on skewness coefficient lies not only in the independence property in the distribution of asset price series, but also in the satisfaction of the important assumption that the asset price series obeys normal distribution. However, the highly significant results
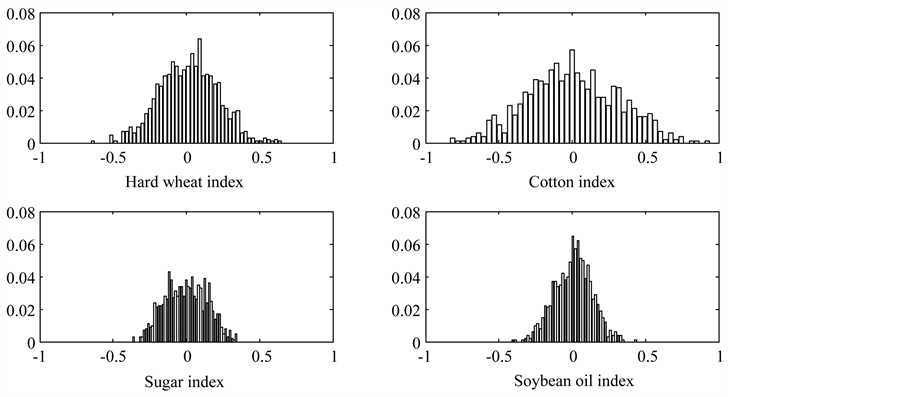
Figure 3. Empirical distribution of indexes’ return series obtained by repeated bootstrap sampling.
of J-B test and Ljung-Box test in table 1 reveal that the test conclusions given by skewness coefficient are very questionable. Compared with asymmetry test based on skewness coefficient, the bootstrap-based one is much more reliable and effective, because we don’t have to make any assumption of specified distribution on the actual data and we let the data speak for themselves. Of course what stated above need to be checked, so in the next part a robustness test will continue to compare the two asymmetry test method empirically.
5. Robustness Test
In this section we will carry on further research on whether the bootstrap-based method actually test asymmetry in return series more accurately and reliably than the asymmetry test based on skewness coefficient. As Lisi (2007) has already confirmed the robustness of results coming from bootstrap-based asymmetry test by means of Monte-Carlo simulation, another robustness test way introduced by Premaratne and Beta (2005) will be adopted in this paper, that is to study bootstrap performance by observing the empirical densities of the return series of the four agricultural futures indexes.
Figure 4 depicts the empirical densities of return series of hard wheat index, cotton index, sugar index and soybean oil index.
In Table 3 we have seen that asymmetry test based on bootstrap and the one based on coefficient of skewness give the same test results on the return series of cotton index and soybean oil index. The return series of cotton index has a significant property of symmetry and the return series of soybean oil index has a significant property of asymmetry. Then in Figure 4 we can also seen from the empirical densities that there is no distinct difference between the property of actual distribution and those test results on return series of cotton and soybean oil index, so both the two methods have given accurate test results in the case of cotton and soybean oil index.
However, the difference between the two methods is mainly reflected in the case of hard wheat and sugar index, so here we need to focus on the empirical densities of return series of hard wheat and sugar index. As is shown in Figure 4, no matter from the aspect of mean value’s location or the aspect of how points distribute around the mean value, we cannot find asymmetry in the actual distribution of return series of hard wheat and sugar index. So we can make a conclusion that, in this situation, results referring to skewness coefficient cannot capture real property of the data while results of bootstrap-based test are much more reliable and accurate.
6. Conclusion and Recommendations for Future Research
In recent years, studies of asymmetry test on distribution of asset return have gradually become a hot issue in the field of financial econometrics. This is not only because that the asymmetry in the distribution of asset return needs to be measured accurately in an optimal portfolio allocation process, but also because that the asymmetry directly determines the adequacy of financial risk identification and the accuracy of risk measurement. However, most of the asymmetry test methods adopted in the researches of return series in Chinese agricultural futures
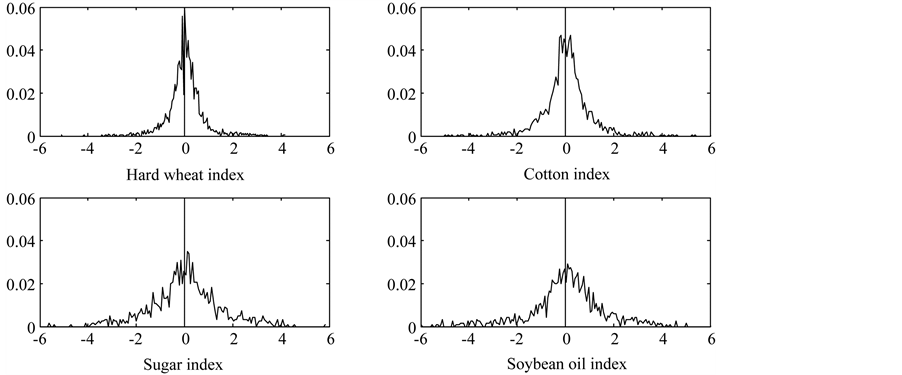
Figure 4. Empirical densities of the four return series.
market are still the conventional skewness coefficient method. The assumptions of independence and normal distribution usually cannot be satisfied by real data, so there is a big problem in the accuracy and reliability of the conclusions given by asymmetry test based on coefficient of skewness.
In order to fix the defect in the asymmetry test based on coefficient of skewness, we adopt an bootstrap-based asymmetry test method proposed by Lisi (2007) to test the asymmetry in the return distribution of four representative price indexes coming from agricultural futures market in China in this article, they are hard wheat index, cotton index, sugar index and soybean oil index. Research results indicate that: except that the distribution of return series of soybean oil index is significantly asymmetric, the rest three ones are significantly symmetric at high significance levels. In the end, this paper also confirms the accuracy and reliability of the results given by bootstrap-based asymmetry test by investigating the empirical densities of the four return series.
The work in this paper has enriched findings of empirical researches on asymmetry in financial return series. At present, the international asymmetry research on financial return series is still in its infancy, and the existing work in this area has led to a general consensus on the significance and importance of the study of asymmetry in asset returns. But questions such as whether the asymmetry significantly existing in financial return series, and what’s the micro-mechanism of asymmetry formation are still controversial. Those controversial points need more theoretical models and empirical results to solve and explain. Therefore, the question of how to explain the empirical conclusions in this study has created ideas for future research, which are, exploring why the distribution of certain financial return (such as return series of soybean oil index in this paper) presents a property of asymmetry which is obviously different from other financial returns’, and finding out what’s the micro-mechanism of asymmetry formation in those return series.
Acknowledgements
The authors would like to acknowledge the referee for their valuable comments. The authors also thank the National Natural Science Foundation of China (No. 71101119) for providing financial support for this work.
References
- Bai, J., & Ng, S. (2005). Test for Skewness, Kurtosis and Normality for Time Series Data. Journal of Business and Economics Statistics, 23, 49-60. http://dx.doi.org/10.1198/073500104000000271
- Bali, T., & Theodossiou, P. (2007). A Conditional-SGT-VaR Approach with Alternative GARCH Models. Annals of Operations Research, 151, 241-267. http://dx.doi.org/10.1007/s10479-006-0118-4
- Bera, A., & Premaratne, G. (2001). Adjusting the Tests for Skewness and Kurtosis for Distributional Misspecifications (Working Paper). Champaign, IL: University of Illinois.
- Christofferson, P. F. (2003). Elements of Financial Risk Management. San Diego, CA: Academic Press.
- Christoffersen, P. F., Heston, S., & Jacobs, K. (2006). Option Valuation with Conditional Skewness. Journal of Econometrics, 131, 253-284. http://dx.doi.org/10.1016/j.jeconom.2005.01.010
- Engle, R. F. (1982). Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica, 50, 987-1007. http://dx.doi.org/10.2307/1912773
- Harvey, C. R., Liechty, J. C., Liechty, M. W., & Muller, P. (2010). Portfolio Selection with Higher Moments. Quantitative Finance, 10, 469-485. http://dx.doi.org/10.1080/14697681003756877
- Karoglou, M. (2009). Breaking Down the Non-Normality of Stock Returns. European Journal of Finance, 16, 79-95. http://dx.doi.org/10.1080/13518470902872343
- Kendall, M., & Stuart, A. (1969). The Advanced Theory of Statistics. New York: McGraw-Hill Press.
- Khalifa, A., Miao, H., & Ramchander, S. (2011). Return Distribution and Volatility Forecasting in Metal Futures Market: Evidence from Gold, Silver and Copper. Journal of Futures Markets, 31, 55-80. http://dx.doi.org/10.1002/fut.20459
- Lisi, F. (2007). Testing Asymmetry in Financial Time Series. Quantitative Finance, 7, 687-696. http://dx.doi.org/10.1080/14697680701283739
- Mcneil, A. J., & Frey, R. (2000). Estimation of Tail Related Risk Measures for Heteroscedastic Financial Time Series: An Extreme Value Approach. Journal of Empirical Finance, 7, 271-300. http://dx.doi.org/10.1016/S0927-5398(00)00012-8
- Peiro, A. (2004). Asymmetries and Tails in Stock Index Returns: Are Their Distributions Really Asymmetric? Quantitative Finance, 4, 37-44. http://dx.doi.org/10.1088/1469-7688/4/1/003
- Premaratne, G., & Bera, A. (2005). A Test for Symmetry with Leptokurtic Financial Data. Journal of Financial Econometrics, 3, 169-187. http://dx.doi.org/10.1093/jjfinec/nbi009
- Rosenberg J. V., & Schuermann, T. (2006). A General Approach to Integrated Risk Management with Skewed, Fat-Tails Risks. Journal of Financial Economics, 79, 569-614. http://dx.doi.org/10.1016/j.jfineco.2005.03.001
- Sabiruzzaman, M., Huq, M., Beg, R. A., & Anwar, S. (2010). Modeling and Forecasting Trading Volume Index: GARCH versus TGARCH Approach. Quarterly Review of Economics and Finance, 50, 141-145. http://dx.doi.org/10.1016/j.qref.2009.11.006
- Samuelson, P. (1970). The Fundamental Approximation of Theorem of Portfolio Analysis in Terms of Means, Variance and Higher Moments. Review of Economic Studies, 37, 537-542. http://dx.doi.org/10.2307/2296483
- Shi, L. M., Wen, B., & Hu, W. X. (2009). The Study on the Relationships of Exchage and Agricultural Products Futures Prices. Journal of Central University of Finance & Economics, 33, 37-42.
- Tang, Y. W., Chen, G., & Zhang, C. H. (2005). An Empirical Research on the Long-Term Correlation of the Price Volatility of the Agricultural Products Futures Markets. Systems Engineering, 23, 79-84.
- Terasvirta, T., & Zhao, Z. (2011). Stylized Facts of Return Series, Robust Estimates and Three Popular Models of Volatility. Applied Financial Economics, 21, 67-94. http://dx.doi.org/10.1080/09603107.2011.523195
- Wang, J., & Zhang, Z. C. (2006). Study of Price Discovery of China’s Farm Produce Futures Based on VAR Model. Chinese Journal of Management, 2, 680-684.
- Yi, R., Zhang, W., Chen, C., & Wang, S. Y. (2010). Agricultural Futures Basis Behaviors Basing on Expectations Theory. Systems Engineering—Theory & Practice, 30, 1954-1959.
NOTES

*Corresponding author.

1The examination of what effect and influence asymmetry should have on the portfolio allocation, risk management and derivatives pricing etc. will be of significance only after we have confirmed the existence of asymmetry in the distribution of financial price (return).


