Journal of Financial Risk Management
Vol.3 No.1(2014), Article ID:44382,10 pages DOI:10.4236/jfrm.2014.31002
Analysing a Pricing Policy for a Home Centre: A Case Study
Dora Maglione1, Angela Diblasi2
1Universidad Nacional de la Patagonia Austral, Santa Cruz, Argentina
2Universidad Nacional de Cuyo, Mendoza, Argentina
Email: dmaglione@disytel.net, angelad@uncu.edu.ar
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 15 December 2013; revised 15 January 2014; accepted 25 January 2014
ABSTRACT
One critical aspect of retailer category management is pricing the items in order to maximize total profits. To define an appropriate pricing policy, a retailer should evaluate how changes in prices of a set of items may impact their shelves or inter demands. In this setting, elasticities play a major role. In addition, a proper policy can be defined from different points of view. In this paper, estimation of a profit function and its maximization under different scenarios is used as a tool to analyze such policy. Estimation of this function is performed through a previous selection of items within a home center category. Then, an adequate AIDS model allowing calculation of elasticities is fitted. Moreover, a profit function is defined in terms of prices and demands. This functionis linearized for the following two purposes, to express it in terms of elasticities, and to maximize it more easily under the consideration of different sets of item prices defined in a convex set. Then, confidence intervals for the total and marginal profits were built to gather the randomness of demands. The results are applied to the selected items in a home center that behaves as a monopoly in the area.
Keywords:Almost Ideal Demand System; Elasticity; Profit Function; Linear Optimization

1. Introduction
Pricing policies can be considered key drivers of the performance of a business. They may become a complicated start-up, and even a permanent problem to cope with. An optimal pricing strategy usually depends on internal management but also on the pricing policy of other retail stores in the area. The latter problem can be avoided when the target business behaves as a monopoly. For this reason and for the sake of simplicity, we conducted this study under the assumption of a monopoly. We also consider that the seller is committed exclusively to finding the best way to obtain the maximum profit. Then, it is assumed that a potential customer’s decision whether or not to purchase an item will depend on price. In this context, our customers are, as characterized by (Lazear, 1986), “buyers”, i.e. those customers who are willing to buy. In addition, it is assumed that demands are random variables and, consequently, we will consider a stochastic model.
When a business involves multiple categories, managing price policy for each category is of concern and importance to the retailer. Yet, he can end up in a blind alley when the number of purchasing categories is too big. A possible way to cope with this problem is estimating a demand system within a category of items to obtain price-demand elasticities.
In this setting, selection of one category is the first step and the one presented in this work. This category is chosen because it includes the most important items from the point of view of their contribution to total income and its rotation, defined as the number of days in the period when they are sold.
Once the items within a category are selected, a model to estimate price and income demands is to be fitted. There are some models proposed in the literature to estimate elasticities. Some examples are the Rotterdam model (Theil, 1965, 1976), the translog model (Christensen, Jorgenson, & Lau, 1975), AIDS (Deaton, & Muellbauer, 1980), Logit (Besanko, Gupta, & Jain, 1998), Translog and AIDS (Attfield, 2004) under the assumption of non-stationarity of the variables involved, just to consider some of the most popular models in the context of consumer theory. In this work, we have fitted some of these models as well as some others and tested their goodness of fit to our data. The model with the best performance was an AIDS one. Because this model depends on a price index for each period, different approaches to this index were considered. Their performances were checked through cross validation with the analysis of prediction errors and some representative statistics for a simultaneous equation system. Then, elasticities can be calculated from this system (Green & Alston, 1990). With the estimated elasticities we were able to estimate total profit. This profit function was linearly approximated by Taylor development using elasticities, and then maximized under different scenarios. In order to gather the random variation in demands, empirical confidence intervals were built for the total profit. This procedure was carried out by generating random samples from the distribution of the demand vector for the selected items. Because of the linear approximation to the profit function, this estimated total profit could be partitioned as the sum of the marginal profit of each item. Then, the methodology presented here is a useful tool at the time of analyzing different pricing policies.
2. A Model to Estimate Elasticities
We have considered the data corresponding to price and demands for 28,267 items which have been selling in a home center in Río Gallegos, Argentina, over a period of 14 months. Around 10% of these items represent 80% of the net profit (cost price minus selling price). The cumulative profit (first row) and number of items to reach it (second row) are displayed in Table 1.
We can observe in this table that only 13 items (over a total of 28,267) represent 20% of the total profit of the home center and 80% of this profit is reached by only 2871 items over a huge total of 28,267. This behavior led to analyze a group of a few items that are most important because of their absolute marginal profit jointly with their rotation, i.e., the number of days in the period in which the item was sold. Nineteen items were chosen based on these two criteria. These items generate 22.5% of the total profit and share a high rotation. Then some items which are not specifically related to building, such as adhesive for ceramic tiles, gas heaters, etc. or those who are only sold to big building companies, as packages of two thousand bags containing fifty kg of cement, were dismissed. The resulting selected items were the twelve ones depicted in Table 2. The order in terms of contribution to total profit (first column) and the number of days in the period in which every item was sold (second column) are shown in this table.
We analyze and compare different models of simultaneous equation demand systems for the selected twelve items, day by day, from September 2005 to January 2010. The aim of this procedure is to choose a model for predicting the budget share of a good in this period and estimate elasticities. Because the AIDS (Almost Ideal
Table 1. Cumulative profit percentage for the period March 07-May 08 and corresponding number of items.
Table 2. The selected twelve items.
Demand System) model proposed by Deaton and Muellbauer (1980) is grounded on a well-structured analytical framework, it allows us to calculate price, demand, and income elasticities. Hence, if 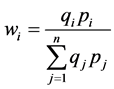 is the budget share of good i, this equation system can be written as:
is the budget share of good i, this equation system can be written as:
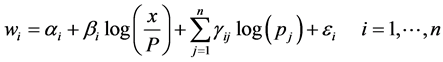 (3.1)
(3.1)
where 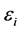 is a random normal variable N(0,s2). The parameters
is a random normal variable N(0,s2). The parameters![]() ,
, ![]() and
and![]() ,
, 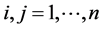 are constrained by:
are constrained by:
 (3.2)
(3.2)
There are some proposals in the literature to calculate the price index P. One of the most widely used among the applications of AIDS system is Stone’s approach, given by:
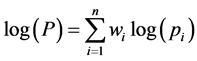 (3.3)
(3.3)
Despite its popularity, this index was brought into question by some people, because it is not related to a base period. To solve this problem, an alternative expression, known as Tornqvist index is
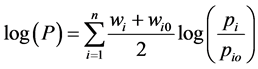 (3.4)
(3.4)
Other classical approach to this index we have resorted to are the two different versions of Laspeyres index
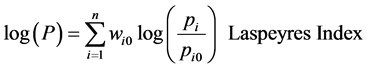 (3.5)
(3.5)
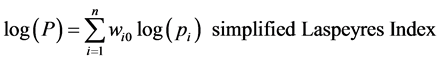 (3.6)
(3.6)
Share budgets wi were calculated through time, for each day t in the period under study. Then, wit is the budget share of item i in the period (day) t. Then, the observed model in Equation (3.1) can be written as:
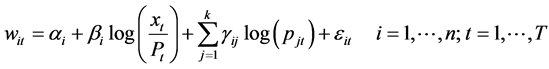 (3.7)
(3.7)
where 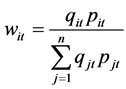 and
and ![]() are random normal variables N(0,s2), and the corresponding versions of Stone and Tornqvist, Laspeyres, and simplified Laspeyres indexes, for each observed day t are:
are random normal variables N(0,s2), and the corresponding versions of Stone and Tornqvist, Laspeyres, and simplified Laspeyres indexes, for each observed day t are:

As regards the distribution of![]() , they have been considered under three different assumptions on the errors, uncorrelated between items and over time, and homoscedastic (OLS); uncorrelated between items and over time but heteroscedastic (WLS), and correlated between items but uncorrelated over time (SUR; Srivastava & Giles 1987). We have estimated these twelve models leaving one day out every time (cross-validation) to analyze the stability of the models through time. The mean squared error of predictions was calculated for each model.
, they have been considered under three different assumptions on the errors, uncorrelated between items and over time, and homoscedastic (OLS); uncorrelated between items and over time but heteroscedastic (WLS), and correlated between items but uncorrelated over time (SUR; Srivastava & Giles 1987). We have estimated these twelve models leaving one day out every time (cross-validation) to analyze the stability of the models through time. The mean squared error of predictions was calculated for each model.
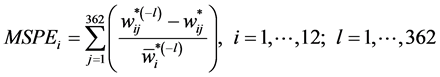 (3.8)
(3.8)
where ![]() is the predicted budget share of good i at time j,
is the predicted budget share of good i at time j, 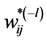 is the predicted budget share of good i at time j calculated without day l, and
is the predicted budget share of good i at time j calculated without day l, and ![]() is the average over time of
is the average over time of ,
, 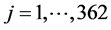 , j ¹ l.
, j ¹ l.
As can be noticed in Figure 1, on day 152, PPS is an outlier for all models. This behavior is explained by the fact that the price of item “hollow brick “HIPER” 08 × 18 × 33 cm” was lowered by 15%. This resulted in a burst of sale of 36,585 units compared with an average of 417 in the period. Then, this day was eliminated from the database to prevent a bias in the estimation procedure.
From the comparison of different statistics and residual behaviors, it was straightforward that the approach using Laspeyres simplified price index for P in Equation (3.1) is better than those using Stone price index. Besides, the goodness of fit of the models with this price index is similar under different assumptions on the type of error dependence. This led us to choose an AIDS model with Laspeyres simplified price index and independent and identically distributed errors following the assumptions on the OLS methodology. Once this model was chosen, it was used to calculate price and income elasticities as well as demand-demand elasticities. As considered in Green & Alston (1990), price elasticities can be written as:
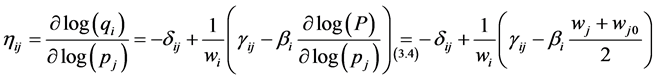
(where ![]() is the Kronecker delta), and income elasticities,
is the Kronecker delta), and income elasticities,

If we define
 (3.9)
(3.9)
price-income elasticities,
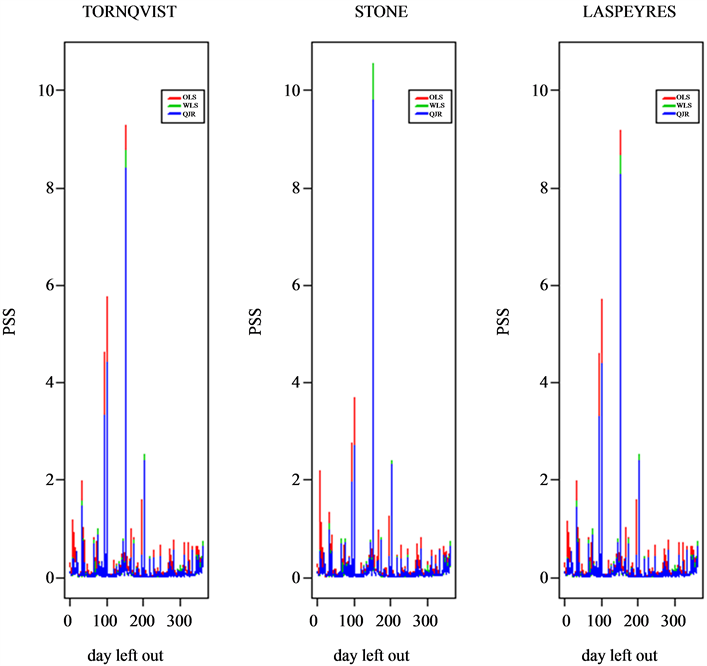
Figure 1. Predicted Sum of Square (PPS) leaving one day out is shown in this figure. In the left panel, models were fitted with Tornqvist approach (Equation (3.4)), in the central panel, they were fitted with Stone’s Equation (3.3)), and in the right panel, they were fitted using Laspeyres proposal (Equations (3.5) and (3.6)).
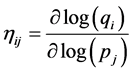 (3.10)
(3.10)
can be calculated from the Equation (3.9) and Model (3.1) as:
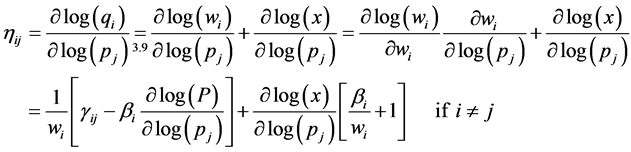 (3.11)
(3.11)
when i = j, elasticity ![]() has an additional term because the derivative of the last term in 3.9 is not null. Then,
has an additional term because the derivative of the last term in 3.9 is not null. Then,
 (3.12)
(3.12)
The expressions 3.11 and 3.12 can be written in one equation by means of the Kroneckerdelta, ![]() , where
, where , if i ¹ j and
, if i ¹ j and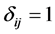 , if i = j.
, if i = j.
 (3.13)
(3.13)
4. Total and Marginal Profit Estimation
4.1. Maximization of a Profit Function under Different Scenarios
Our aim now is to build a tool that allows for a response to one of the most typical starting point for discussions about pricing: how to charge the different items in order to maximize profit. This purpose led us to estimate a profit function in order to analyze different pricing scenarios. Once elasticities are estimated, a profit function can be maximized as a linear function. In fact, elasticities will allow us to approximate this function using a Taylor’s polynomial and maximize it by resorting to linear programming tools in a convex set. We defined this function as:
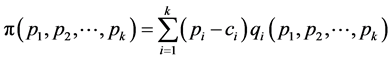 (4.14)
(4.14)
where ci, is the cost of item which is considered constant (maximum value), over the period under study, i,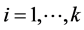 . Then,
. Then,
 (4.15)
(4.15)
where x is the total income in the period. In this context, we consider the situation in which this total income remains constant over the period.
This means that
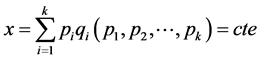 (4.16)
(4.16)
A variation in item i can be introduced by the amount 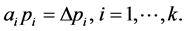 Then, the variation in the random function
Then, the variation in the random function 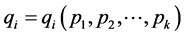 between points
between points  and
and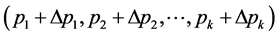 can be approximated by Taylor’s linear polynomial as:
can be approximated by Taylor’s linear polynomial as:
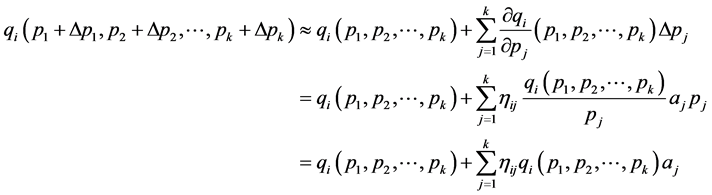
Then the variation in the profit function is

A variation 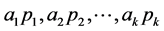 in the prices
in the prices 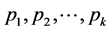 respectively, results in a variation in profit that can be approximated by,
respectively, results in a variation in profit that can be approximated by,
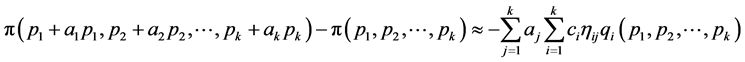 (4.17)
(4.17)
This expression can be maximized as a function of ai, 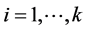 in a convex set defined by the minimum and maximum values given to the proportion of increase or diminution in the price of each item. The values of ai
in a convex set defined by the minimum and maximum values given to the proportion of increase or diminution in the price of each item. The values of ai
for which the previous difference is maximum can be expressed as: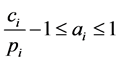 . In this way, we consider a price variation of an item between its cost and twice its cost. Three scenarios were analyzed as examples of pricing policies and their results using this methodology.
. In this way, we consider a price variation of an item between its cost and twice its cost. Three scenarios were analyzed as examples of pricing policies and their results using this methodology.
4.1.1. Scenario 1
The prices of all items can be moved within a range of . This means that the profit function should be maximized in the set
. This means that the profit function should be maximized in the set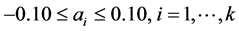 . An example of this pricing policy is shown in Table 3 where maximization of the profit function led to a drop in the prices of cement, hollow brick, whitewash, and zinc, and a rise in price in the remaining items.
. An example of this pricing policy is shown in Table 3 where maximization of the profit function led to a drop in the prices of cement, hollow brick, whitewash, and zinc, and a rise in price in the remaining items.
4.1.2. Scenario 2
We considered an alternative pricing policy by fixing all prices except those for cement and different kinds of bricks (excepting grey hollow brick). In other words, we maximized the increment of the profit function under the restrictions: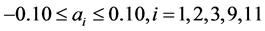 . The resulting values of final and initial prices are shown in Table 4. In this setting, the net gain is 20.67%. This represents almost half the total profit in the scenario but with the third part of the item prices released.
. The resulting values of final and initial prices are shown in Table 4. In this setting, the net gain is 20.67%. This represents almost half the total profit in the scenario but with the third part of the item prices released.
4.1.3. Scenario 3
In this scenario, all prices are fixed except for those corresponding to different kinds of iron. Again, they can change in a proportion of between −0.10 and 0.10. The results before and after maximizing the profit function are shown in Table 5. The net gain in this scenario is 6.1%.
Table 3. Final and initial prices resulting from maximizing the profit function when all prices can vary in a proportion of between −0.10 and 0.10.
Table 4. Final and initial prices resulting from maximizing the profit function when all prices, except for those in bold characters, can vary in a proportion of between −0.10 and 0.10.
4.2. Empirical Confidence Intervals
For the purpose of including the random effects of the demands considered, empirical confidence intervals were built based on the prices maximizing total gain. This was done for each scenario by fixing the corresponding prices and generating 1000 random samples from independent normal components of the vector containing the log-demand for each article. As parameters of these normal distributions we considered sample means and variances calculated for the last thirty days. Marginal intervals for each item’s profit can be calculated due to the linear approach (4.17).
Scenario 1: The 95%-interval for the total profit calculated with the prices maximizing this profit under scenario 1 was (34552.1, 36591.27). Thus, an estimated percentage for this total profit would vary between 34.72 and 42.67%. In Table 6, marginal confidence intervals are calculated for each item’s profit. Because of the linear approximation to the profit function, the estimated percentage of the total profit under this scenario can be written as the sum of these estimated marginal profits.
Scenario 2: The 95%-interval for the total profit calculated with the prices maximizing this profit under scenario 2 was (30279.50, 31618.85). In this case an estimated percentage for this total profit would vary between 18.06 and 23.28%. In Table 7, marginal confidence intervals are calculated for each item’s profit under this scenario.
Scenario 3: The items selected in this Scenario were those representing different diameters of iron bars. The simulation procedure generated the 95% interval for total profit as (27068.85, 27361.33) corresponding to a variation between 5.54 and 6.68%. The item corresponding to iron bars of 10 mm is not in Table 8 because its price was not modified in the process of maximizing the profit function.
Table 5. Final and initial prices resulting from maximizing the profit function when all prices, except those for iron, can vary in a proportion of between −0.10 and 0.10.
Table 6. 95% confidence intervals and their corresponding percentage intervals for each item in column 1 are shown in columns 2 and 3. Reference prices are considered under scenario 1.
Table 7. 95% confidence intervals and their corresponding percentage intervals for those items (Column 1) whose prices were modified (Scenario 2) are shown in Columns 2 and 3.
Table 8. 95% confidence intervals and their corresponding percentage intervals for those items (Column 1) whose prices were modified (Scenario 3) are shown in Columns 2 and 3.
• 5. Some Conclusions
• An appropriate version of AIDS, when possible, guarantees properties of utility function and has allowed us to estimate elasticities.
• These elasticities were used to build a profit function and obtain its variation when price variations are present. In addition, this analysis allows obtaining approximations to the variation in the profit function underpricing variations. This information is, indeed, crucial when a business specialist has to make decisions about the profit maximization.
• In this work, we have analyzed three scenarios, as an example to define pricing policies and their effects on the profit function when this is maximized.
• The linear approximation to this profit function we used here has the advantage of simplifying its maximization through a standard program designed to optimize a linear function subject to constraints. In addition, it can be written as a linear combination of the marginal profits due to each item.
• Empirical distribution of this approximate linear profit function, under normally distributed log-demands, can provide empirical confidence intervals for the maximum profit under different scenarios. Thus, the random variation of this maximum profit can be quantified for each item as a marginal interval.
• The AIDS fitted to data can also be replaced by another way of estimating elasticities. Still they can be used to build a profit function and its linearization to maximize straightforwardness. Additionally, and as pointed out before, it results in a linear combination of marginal profits.
Although the methodology used here was built for a home centre which behaves as a monopoly, it can be the starting point to considering additional assumptions.
References
- Attfield, C. (2004). Comparison of the Translog and Almost Ideal Demand System. Discussion Paper 04/564, Bristol: Department of Economics, University of Bristol.
- Besanko, D., Gupta, S., & Jain, D. (1998). Logit Demand Estimation under Competitive Pricing Behavior. Management Science, 44, 1533-1547. http://dx.doi.org/10.1287/mnsc.44.11.1533
- Christensen, R., Jorgenson, L. W., & Lau, L. J. (1975). Transcendental Logarithmic Utility Functions. The American Economic Review, 65, 367-383.
- Deaton, A., &Muellbauer, J. (1980). An Almost Ideal Demand System. The American Economic Review, 70, 312-326.
- Green, R., & Alston, J. (1990). Elasticities in AIDS Models. American Journal of Agricultural Economics, 72, 442-445. http://dx.doi.org/10.2307/1242346
- Lazear, E. P. (1986). Retail Pricing and Clearance Sales. The American Economic Review, 76, 14-32.
- Srivastava, V., & Giles, D. (1987). Seemingly Unrelated Regression Equations Models: Estimation and Inference. New York: Marcel Dekker.
- Theil, H. (1965). The Information Approach to Demand Analysis. Econometrika, 33, 67-87. http://dx.doi.org/10.2307/1911889
- Theil, H. (1976). Theory of Measurement of Consumer Demand. Econometrika, 33, 67-87. http://dx.doi.org/10.2307/1911889


