International Journal of Modern Nonlinear Theory and Application
Vol.05 No.03(2016), Article ID:70881,10 pages
10.4236/ijmnta.2016.53013
Chaos in a Fractional-Order Single-Machine Infinite-Bus Power System and Its Adaptive Backstepping Control
Zhanhong Liang, Jinfeng Gao
School of Electrical Engineering, Zhengzhou University, Zhengzhou, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 18, 2016; Accepted: September 24, 2016; Published: September 27, 2016
ABSTRACT
This paper has numerically studied the dynamical behaviors of a fractional-order single-machine infinite-bus (FOSMIB) power system. Periodic motions, period- doubling bifurcations and chaotic attractors are observed in the FOSMIB power system. The existence of chaotic behavior is affirmed by the positive largest Lyapunov exponent (LLE). Based on the fractional-order backstepping method, an adaptive controller is proposed to suppress chaos in the FOSMIB power system. Numerical simulation results demonstrate the validity of the proposed controller.
Keywords:
Power System, Fractional Calculus, Chaos, Backstepping Method

1. Introduction
As a mathematical branch with a history of over 300 years, fractional calculus and its applications to physics and engineering have attracted increasing attentions in recent years [1] [2] . Fractional calculus provides a good instrument to describe the memory, hereditary, non-locality and self-similarity properties of various materials and processes. Many chaotic systems, such as Lorenz system [3] , Chua’s system [4] , Duffing system [5] , Rössler system [6] , Chen system [7] and so on, still remain chaotic when their equations become fractional.
Chaotic phenomena have been observed in power systems during the past few decades [8] - [13] . Chaos causes electromechanical oscillations to behave randomly, which are harmful to the secure and stable operation of power systems, and even produce undesired negative consequences, such as angle divergence, voltage collapse and system splitting [14] . So far, almost all the studies of dynamics of power systems are concerned with the integer-order models, and there are little research results on fractional modeling and control design of power systems. Tan et al. studied the dynamics of a fractional-order interconnected power system and found that the system became chaotic when the fractional order is no less than 0.88 [15] . Sun and Li investigated the chaotic and bifurcation phenomena in a fractional-order three-bus power system and the existence of chaos was demonstrated for different orders [16] .
In this paper, we numerically investigate the chaotic dynamics of a fractional-order single-machine infinite-bus (FOSMIB) power system. Period-doubling bifurcation and chaos are observed in FOSMIB power system and the existence of chaos is confirmed by evaluating the largest Lyapunov exponent (LLE). Based on the fractional-order backstepping method, an adaptive controller is presented to suppress chaos in the FOSMIB power system, and the effectiveness of the proposed controller is proved by the numerical simulation results.
The rest of the paper is organized as follows. Some definitions and lemmas about fractional calculus are introduced in Section 2. The dynamics of the FOSMIB power system are analyzed in Section 3. An adaptive controller is designed using the fractional-order backstepping method to suppress chaos in the FOSMIB power system in Section 4. Finally, conclusions are addressed in Section 5.
2. Preliminaries
There are several different definitions of fractional derivatives. The most appropriate one for practical problems is the Caputo definition. The Caputo fractional derivative is given by
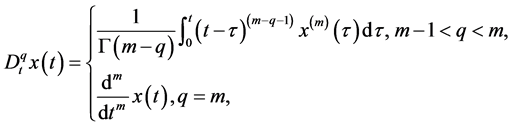 (1)
(1)
where m is integer and 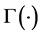 is the Gamma function.
is the Gamma function.
The Caputo fractional derivative satisfies the following properties:
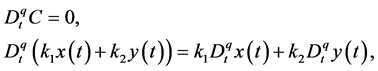 (2)
(2)
where C, 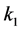 and
and 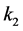 are real constants.
are real constants.
Lemma 1. [17] - [19] Consider the fractional-order system
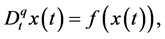 (3)
(3)
where 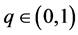 and
and . The equilibrium point
. The equilibrium point  of system (3) is locally asymptotically stable if all the eigenvalues
of system (3) is locally asymptotically stable if all the eigenvalues 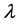 of the Jacobian matrix
of the Jacobian matrix 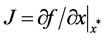 satisfy
satisfy
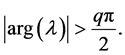 (4)
(4)
Lemma 2. [20] Let  be a continuous differentiable function. Then, at any instant the following inequality holds
be a continuous differentiable function. Then, at any instant the following inequality holds
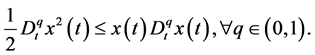 (5)
(5)
A continuous function  is referred as class-K if it is strictly increasing and
is referred as class-K if it is strictly increasing and  [21] .
[21] .
Lemma 3. (Fractional-order extension of Lyapunov direct method [22] ) Let  be an equilibrium point of the nonautonomous fractional-order system
be an equilibrium point of the nonautonomous fractional-order system
 (6)
(6)
with initial condition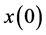
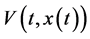
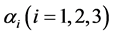
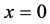
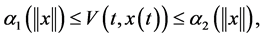
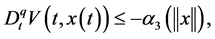
where 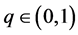

3. The FOSMIB Power System
In [12] Chen et al. analyzed the angle dynamics of the classical single-machine infinite-bus (SMIB) power system, which is governed by the so-called swing equation
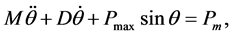
where M is the moment of inertia, D is the damping constant, 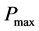
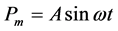
Let 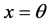
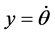
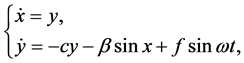
where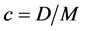
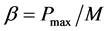
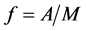
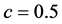
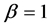
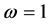
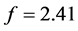
Here, we consider the fractional-order single-machine infinite-bus (FOSMIB) power system
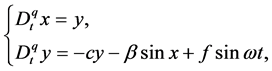
where 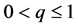
The autonomous system (11) (as
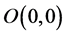
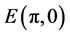
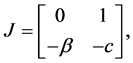
and its eigenvalues are
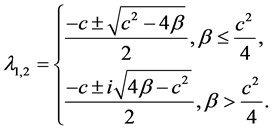
In both cases,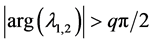
For the equilibrium point E, the Jacobian matrix is
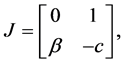
and its eigenvalues are
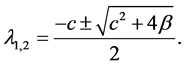
It can be seen that 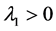
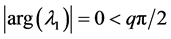
4. Dynamic Analysis of the FOSMIB Power System
In this section, we use the Adams-Bashforth-Moulton predictor-corrector algorithm proposed by Diethelm et al. in [22] - [24] to solve the FOSMIB power system (11). The dynamics are numerically analyzed by means of bifurcation diagrams, phase portraits and Lyapunov exponents. In the following simulations, parameter f is chosen as bifurcation parameter and the other parameters are fixed at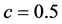
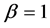
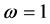
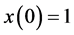
First, let
Figure 1. Bifurcation diagram and the LLE versus f for q = 0.95: (a) Bifurcation diagram; (b) The LLE.
algorithm [25] and plotted in Figure 1(b). The FOSMIB power system is chaotic over most of the range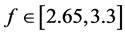
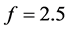
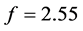
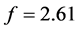
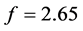
Now, let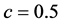
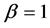
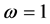
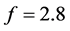
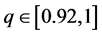
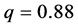
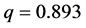
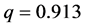
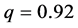
5. Adaptive Backstepping Control of Chaos
In this section, an active controller is designed using fractional-order backstepping method to suppress chaos in the FOSMIB power system and stabilize it to the unstable equilibrium point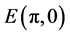
5.1. Controller Design
Consider the controlled FOSMIB power system
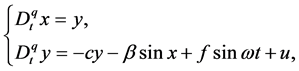
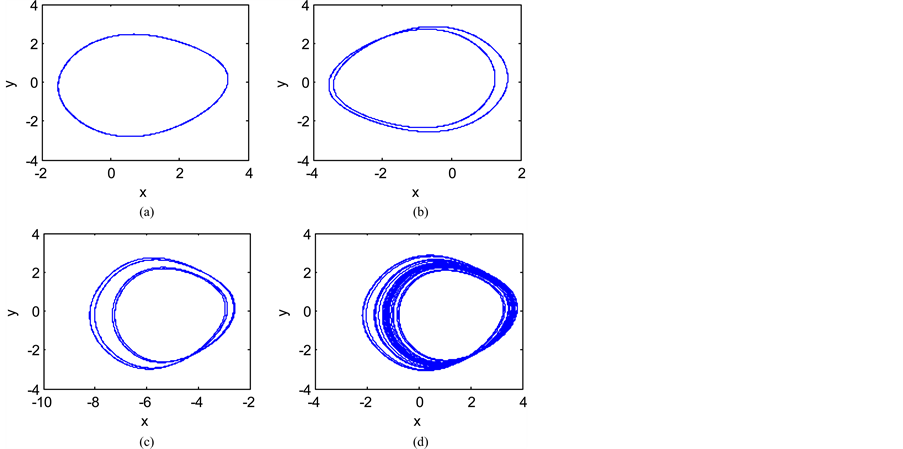
Figure 2. Phase portraits for different values of f: (a) f = 2.5; (b) f = 2.55; (c) f = 2.61; (d) f = 2.65.
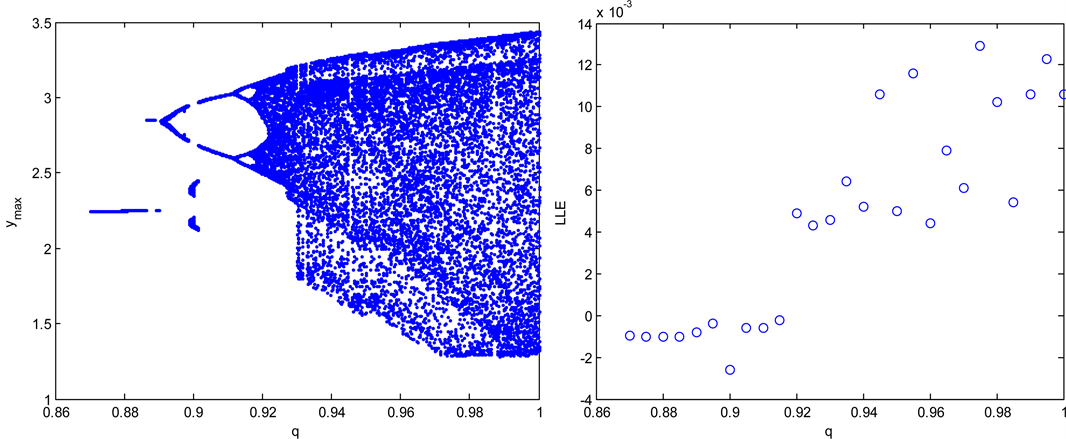
Figure 3. Bifurcation diagram and the LLE versus q for f = 2.8: (a) Bifurcation diagram; (b) The LLE.
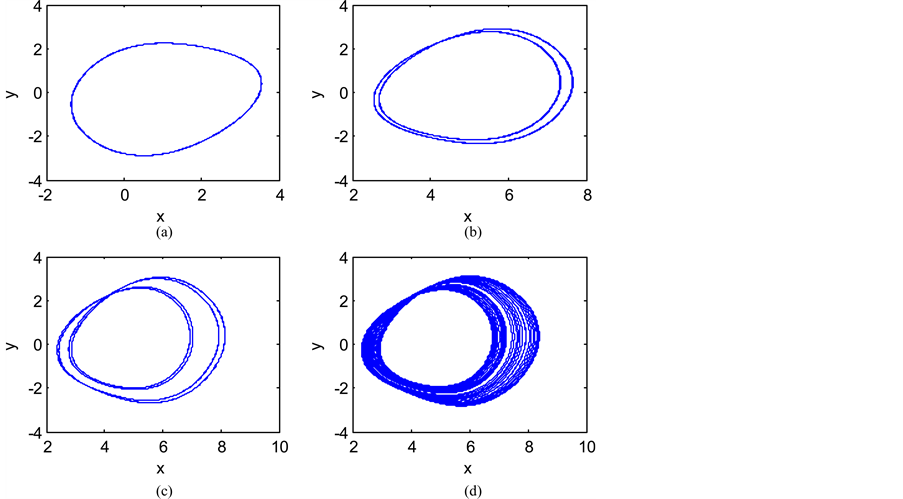
Figure 4. Phase portraits for different values of q: (a) q = 0.88; (b) q = 0.893; (c) q = 0.913; (d) q = 0.92.
where 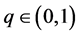
Step 1. Define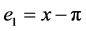
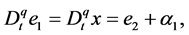
where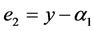
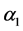
Select the candidate Lyapunov function as
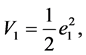
Now, applying Lemma 2, it can be found that
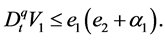
Define the virtual control 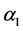
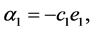
where 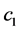
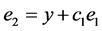
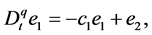
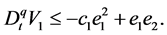
Step 2. The derivative of 
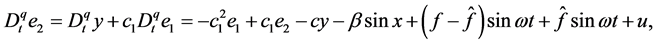
where 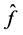
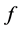
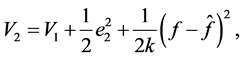
where k is a positive constant, which can adjust the speed of the adaptive law. Using Lemma 2, it can be found that
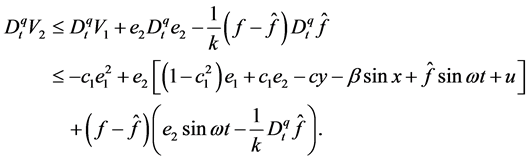
Choose the control input and the adaptive law as
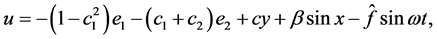
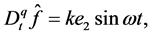
where 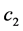
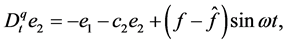
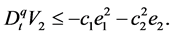
According to Lemma 3, the closed-loop error system is asymptotically stable at the origin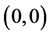
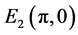
5.2. Simulation Results
In the simulation, the fractional order q is equal to 0.95. The parameters of system (16) are taken as
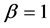
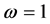
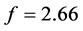
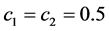
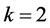
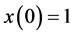
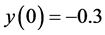
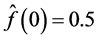
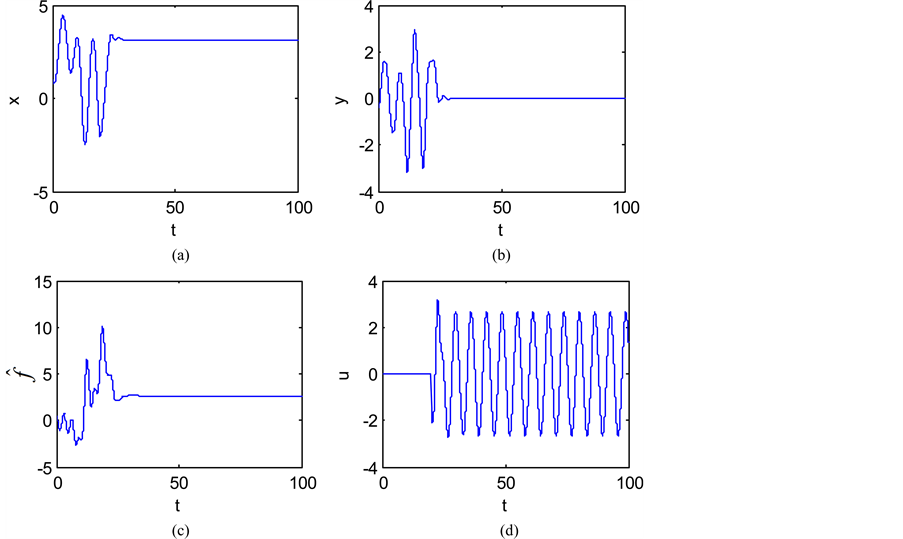
The time-domain waveforms the states of the controlled system (16) are shown in Figure 5(a) and Figure 5(b). The FOSMIB power system has experienced chaotic behavior before the controller is put into effect. By activating the controller u at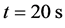
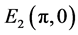
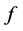
6. Conclusion
In this paper, we have numerically investigated the FOSMIB power system. The parameter f and the fractional order q are selected as bifurcation parameters respectively. Complex dynamical behaviors, such as periodic orbits, period-doubling bifurcations and chaotic attractors, are observed in the FOSMIB power system. The LLE is calculated using Wolf algorithm to confirm the existence of chaos. Furthermore, by exploiting the fractional-order backstepping method, we propose an adaptive controller to suppress chaos in the FOSMIB power system. The effectiveness of the presented controller is verified by numerical simulation results.
Figure 5. The time-domain waveforms of the controlled system (16).
Acknowledgements
The work was supported by the Natural Science Foundation of Henan Province, China (Grant No. 14A120005) and Excellent Young Scientist Development Foundation of Zhengzhou University, China (Grant No. 1421319086).
Cite this paper
Liang, Z.H. and Gao, J.F. (2016) Chaos in a Fractional-Or- der Single-Machine Infinite-Bus Power System and Its Adaptive Backstepping Control. International Journal of Modern Nonlinear Theory and Application, 5, 122-131. http://dx.doi.org/10.4236/ijmnta.2016.53013
References
- 1. Podlubny, I. (1999) Fractional Differential Equations. Academic Press, New York.
- 2. Hilfer, R. (2001) Applications of Fractional Calculus in Physics. World Scientific, New Jersey.
- 3. Grigorenko, I. and Grigorenko, E. (2003) Chaotic Dynamics of the Fractional Lorenz System. Physical Review Letters, 91, Article ID: 034101.
http://dx.doi.org/10.1103/PhysRevLett.91.034101 - 4. Hartley, T.T., Lorenzo, C.F. and Qammer, H.K. (1995) Chaos in a Fractional Order Chua’s System. IEEE Transactions on Circuits and Systems CAS-I, 42, 485-490.
http://dx.doi.org/10.1109/81.404062 - 5. Gao, X. and Yu, J.B. (2005) Chaos in the Fractional Order Periodically Forced Complex Duffing’s Oscillators. Chaos, Solitons and Fractals, 24, 1097-1104.
http://dx.doi.org/10.1016/j.chaos.2004.09.090 - 6. Li, C.G. and Chen, G.R. (2004) Chaos and Hyperchaos in the Fractional-Order Rossler Equations. Physica A, 341, 55-61.
http://dx.doi.org/10.1016/j.physa.2004.04.113 - 7. Li, C.P. and Peng, G.J. (2005) Chaos in Chen’s System with a Fractional Order. Chaos, Solitons and Fractals, 22, 443-450.
http://dx.doi.org/10.1016/j.chaos.2004.02.013 - 8. Kopell, N. and Washburn, R.B. (1982) Chaotic Motions in the Two-Degree-Of-Freedom Swing Equations. IEEE Transactions on Circuits and Systems, 29, 738-746.
http://dx.doi.org/10.1109/TCS.1982.1085094 - 9. Lee, B. and Ajjarapu, V. (1993) Period-Doubling Route to Chaos in an Electrical Power System. IEE Proceedings C-Generation, Transmission and Distribution, 140, 490-496.
http://dx.doi.org/10.1049/ip-c.1993.0071 - 10. Chiang, H.D., Conneen, T.P. and Flueck, A.J. (1994) Bifurcations and Chaos in Electric Power Systems: Numerical Studies. Journal of the Franklin Institute, 331, 1001-1036.
http://dx.doi.org/10.1016/0016-0032(94)90095-7 - 11. Ji, W. and Venkatasubramanian, V. (1996) Hard-Limit Induced Chaos in a Fundamental Power System Model. International Journal of Electrical Power and Energy Systems, 18, 279-295.
http://dx.doi.org/10.1016/0142-0615(95)00066-6 - 12. Chen, H.K., Lin, T.N. and Chen, J.H. (2005) Dynamic Analysis, Controlling Chaos and Chaotification of a SMIB Power System. Chaos, Solitons and Fractals, 22, 1307-1315.
http://dx.doi.org/10.1016/j.chaos.2004.09.081 - 13. Gholizadeh, H., Hassannia, A. and Azarfar, A. (2013) Chaos Detection and Control in a Typical Power System. Chinese Physics B, 22, 10503-10507.
http://dx.doi.org/10.1088/1674-1056/22/1/010503 - 14. Yu, Y.X., Jia, H.J., Li, P. and Su, J.F. (2003) Power System Instability and Chaos. Electric Power Systems Research, 65, 187-195.
http://dx.doi.org/10.1016/S0378-7796(02)00229-8 - 15. Tan, W., Zhang, M. and Li, Z.P. (2011) Chaotic Oscillation of Interconnected Power System and Its Synchronization. Journal of Hunan University of Science and Technology (Natural Science Edition), 26, 74-78. (In Chinese)
- 16. Sun, F.Y. and Li, Q. (2014) Dynamic Analysis and Chaos of the 4D Fractional-Order Power System. Abstract and Applied Analysis, 2014, Article ID: 534896.
http://dx.doi.org/10.1155/2014/534896 - 17. Ahmed, E., El-Sayed, A.M.A. and El-Saka, H.A.A. (2007) Equilibrium Points, Stability and Numerical Solutions of Fractional-Order Predator—Prey and Rabies Models. Journal of Mathematical Analysis and Applications, 325, 542-553.
http://dx.doi.org/10.1016/j.jmaa.2006.01.087 - 18. Tavazoei, M.S. and Haeri, M. (2007) A Necessary Condition for Double Scroll Attractor Existence in Fractional-Order Systems. Physics Letters A, 367, 102-113.
http://dx.doi.org/10.1016/j.physleta.2007.05.081 - 19. Tavazoei, M.S. and Haeri, M. (2008) Chaotic Attractors in Incommensurate Fractional Order Systems. Physica D: Nonlinear Phenomena, 237, 2628-2637.
http://dx.doi.org/10.1016/j.physd.2008.03.037 - 20. Aguila-Camacho, N., Duarte-Mermoud, M.A. and Gallegos, J.A. (2014) Lyapunov Functions for Fractional Order Systems. Communications in Nonlinear Science and Numerical Simulation, 19, 2951-2957.
http://dx.doi.org/10.1016/j.cnsns.2014.01.022 - 21. Li, Y., Chen, Y.Q. and Podlubny, I. (2009) Mittag-Leffler Stability of Fractional Order Nonlinear Dynamic Systems. Automatica, 45, 1965-1969.
http://dx.doi.org/10.1016/j.automatica.2009.04.003 - 22. Diethelm, K., Ford, N.J. and Freed, A.D. (2002) A Predictor-Corrector Approach for the Numerical Solution of Fractional Differential Equations. Nonlinear Dynamics, 29, 3-22.
http://dx.doi.org/10.1023/A:1016592219341 - 23. Diethelm, K. (1997) An Algorithm for the Numerical Solution of Differential Equations of Fractional Order. Electronic Transactions on Numerical Analysis, 5, 1-6.
- 24. Diethelm, K. and Ford, N.J. (2002) Analysis of Fractional Differential Equations. Journal of Mathematical Analysis and Applications, 265, 229-248.
http://dx.doi.org/10.1006/jmaa.2000.7194 - 25. Wolf, A., Swift, J.B., Swinneya, H.L. and Vastano, J.A. (1985) Determining Lyapunov Exponents from a Time Series. Physica D: Nonlinear Phenomena, 16, 285-317.
http://dx.doi.org/10.1016/0167-2789(85)90011-9