International Journal of Modern Nonlinear Theory and Application
Vol.04 No.03(2015), Article ID:58922,13 pages
10.4236/ijmnta.2015.43014
Inertial Manifolds for 2D Generalized MHD System
Zhaoqin Yuan, Liang Guo, Guoguang Lin*
Department of Mathematics, Yunnan University, Kunming, China
Email: 15925159599@163.com, *yuanzq091@163.com, *gglin@ynu.edu.cn.
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 June 2015; accepted 16 August 2015; published 20 August 2015
ABSTRACT
In this paper, we prove the existence of inertial manifolds for 2D generalized MHD system under the spectral gap condition.
Keywords:
MHD System, Spectral Gap, Inertial Manifolds

1. Introduction
In [1] , Yuan, Guo and Lin prove the existence of global attractors and dimension estimation of a 2D genera- lized magnetohydrodynamic (MHD) system:
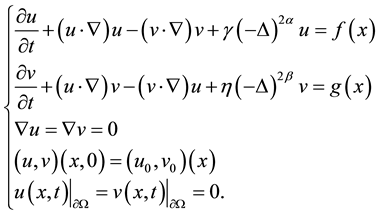 (1.1)
(1.1)
where u is the fluid velocity field, v is the magnetic field, 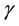 is the constant kinematic viscosity and
is the constant kinematic viscosity and 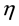 is constant magnetic diffusivity.
is constant magnetic diffusivity. 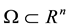 is a bounded domain with a sufficiently smooth boundary
is a bounded domain with a sufficiently smooth boundary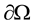 ,
,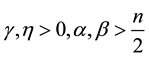 . More results about inertial manifolds can be founded in [2] - [11] .
. More results about inertial manifolds can be founded in [2] - [11] .
In this paper, we consider the following 2D generalized MHD system:
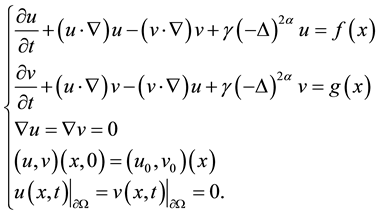 (1.2)
(1.2)
where u is the fluid velocity field, v is the magnetic field, 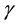 is the constant kinematic viscosity and
is the constant kinematic viscosity and 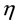 is the constant magnetic diffusivity.
is the constant magnetic diffusivity. 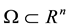 is a bounded domain with a sufficiently smooth boundary
is a bounded domain with a sufficiently smooth boundary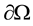 ,
, 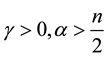 .
.
This paper is organized as follows. In Section 2, we introduce basic concepts concerning inertial manifolds. In Section 3, we obtain the existence of the inertial manifolds.
2. Preliminaries
We rewrite the problem (1.2) as a first order differential equation, the problem (1.2) is equivalent to:
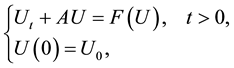 (2.1)
(2.1)
where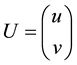 ,
, 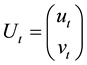 , and
, and
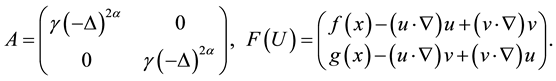
Let H is a Banach space, 








Definition 2.1. Suppose 

1. M is a finite dimensional Lipshitz manifold;
2. M is positively invariant under


3. M is attracts every trajectory exponentially, i.e., for every
We now recall some notions. Let 

Standing Hypothesis 2.2. We suppose that 








Let now 



Let the bound absorbing set


Suppose that 

Denote by 





Lemma 2.3. Defined by 




where
Proof. Assume




where

Lemma 2.3 is proved.
Lemma 2.4. Let 




otherwise, there exist constants 



and

for all
Proof. Let 





Putting

For

From Equation (2.13) and Equation (2.15), we have

We notice that Equation (2.14)
so we have

By Equation (2.16) and Equation (2.17), and use the Cauchy-Schwarz inequality, we obtain

Then using Lemma 2.3,we have
For


where 
By multiplying (2.13) by

Using Holder inequality, from Equation (2.20) we have

In Equation (2.19) setting

where

By Equation (2.21) and Equation (2.22), we have

Integrating Equation (2.24) between 0 and

To complete the proof of Lemma 2.4, we consider the following two cases,

and

We only consider Equation (2.26), in this case,

where 


since



then we obtain

Integrating Equation (2.30) between 0 and
3. Inertial Manifolds
In this section we will prove the existence of the inertial manifolds for solutions to the problem (2.1). We suppose that 

Let constants 



Note that

is the distance of

For every 


possesses a unique solution

where 




by


We need to prove the following two conclusions:
1. For 


2. 

So we give the following Lemmas.
Lemma 3.1. Let

Proof. The proof is similar to Temam [3] .
Lemma 3.2. Let



and

Proof. For any 




and

which proves Equation (3.8). We now prove Equation (3.9), by the definition of

And we have

Substituting Equation (3.13) into Equation (3.11) we obtain Equation (3.9). Lemma 3.2 is proved.
Lemma 3.3. Let





Proof. Let



Let 


So we obtain

Further more, for

Setting 



Lemma 3.3 is proved.
Lemma 3.4. Let

so for every

here



Proof. For any given


and

here 


Multiplying the first equation in Equation (3.25) by

So we have

For

By Lemma 2.3, to do the following estimate,using Equation (3.11) and Equation (3.28) we obtain

here

here
Hence,

Then from Equation (3.15) we have

Combining Equation (3.31) and Equation (3.32), we obtain

Substituting Equation (3.33) into Equation (3.29), we obtain
Lemma 3.4 is proved.
Lemma 3.5. Let 


here 


Proof. Let 


From the first inequality of Equation (3.26) and the following estimate, we have
then from the last inequality of Equation (3.35), we obtain

From Equation (3.36), we have

Due to


From Equation (3.6), Equation (3.35) and Equation (3.38), we have

Then using Equation (3.16), Equation (3.33) and

Lemma 3.5 is proved.
Lemma 3.6. Suppose that


we have 



Proof. From 

where 


To make


Equation (3.46) is equivalent to

If Equation (3.48) is satisfied, so Equation (3.47) is equivalent to 

Suppose that Equation (3.41) is equivalent to

Hence,

Hence,

Therefore Equation (3.49) follows from Equation (3.52). From Equation (3.41) we conclude that



we notice that
From Lemma 3.1 to Lemma 3.6,we can obtain the following conclusions.
Theorem 3.1. Suppose that 








Theorem 3.2. Suppose that 





where

Proof. Let 






Assume 



Let 




Substituting 


If Equation (3.56) is satisfied, assume

In a word, for



Theorem 3.2 is proved.
Supported
This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11161057.
Cite this paper
ZhaoqinYuan,LiangGuo,GuoguangLin, (2015) Inertial Manifolds for 2D Generalized MHD System. International Journal of Modern Nonlinear Theory and Application,04,190-203. doi: 10.4236/ijmnta.2015.43014
References
- 1. Yuan, Z.Q., Guo, L. and Lin, G.G. (2015) Global Attractors and Dimension Estimation of the 2D Generalized MHD System with Extra Force. Applied Mathematics, 6, 724-736.
http://dx.doi.org/10.4236/am.2015.64068 - 2. Lin, G.G. (2009) An Inertial Manifold of the 2D Swift-Hohenberg Equation. Journal of Yunnan University, 31, 334-340.
- 3. Temam, R. (1988) Infinite Dimensional Dynamical Systems in Mechanics and Physics. Springer, New York.
http://dx.doi.org/10.1007/978-1-4684-0313-8 - 4. Constantin, P., Foias, C., Nicolaenko, B. and Temam, R. (1989) Integral Manifolds and Inertial Manifolds for Dissipative Partial Differential Equations. Springer, New York.
http://dx.doi.org/10.1007/978-1-4612-3506-4 - 5. Lin, G.G. (2011) Nonlinear Evolution Equations. Yunnan University, Kunming.
- 6. Babin, A.V. and Vishik, M.I. (1992) Attractors of Evolution Equations. North-Holland, Amsterdam.
- 7. Chow, S.-N. and Lu, K. (1988) Invariant Manifolds for Flows in Banach Spaces. Journal of Differential Equations, 74, 285-317.
http://dx.doi.org/10.1016/0022-0396(88)90007-1 - 8. Chueshov, I.D. (1992) Introduction to the Theory of Inertial Manifolds, (Lecture Notes). Kharkov Univ. Press, Kharkov (in Russian).
- 9. Chueshov, I.D. (1999) Introduction to the Theory of Infinite-Dimensional Dissipative Systems. Acta, Kharkov (in Russian) (English Translation, 2002, Acta, Kharkov).
- 10. Henry, D. (1981) Geometric Theory of Semilinear Parabolic Equations, Lecture Notes in Math. 840. Springer, Berlin-Heidelberg and New York.
- 11. Leung, A.W. (1989) Systems of Nonlinear Partial Differential Equations: Applications to Biology and Engineering. MIA, Kluwer, Boston.
NOTES
*Corresponding author.




















