International Journal of Modern Nonlinear Theory and Application
Vol.03 No.05(2014), Article ID:51250,10 pages
10.4236/ijmnta.2014.35022
Kalman Filters versus Neural Networks in Battery State-of-Charge Estimation: A Comparative Study
Ala A. Hussein
Department of Electrical Engineering, UAE University, Al Ain, UAE
Email: ala.hussein@uaeu.ac.ae
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 September 2014; revised 9 October 2014; accepted 17 October 2014
ABSTRACT
Battery management systems (BMS) must estimate the state-of-charge (SOC) of the battery accurately to prolong its lifetime and ensure a reliable operation. Since batteries have a wide range of applications, the SOC estimation requirements and methods vary from an application to another. This paper compares two SOC estimation methods, namely extended Kalman filters (EKF) and artificial neural networks (ANN). EKF is a nonlinear optimal estimator that is used to estimate the inner state of a nonlinear dynamic system using a state-space model. On the other hand, ANN is a mathematical model that consists of interconnected artificial neurons inspired by biological neural networks and is used to predict the output of a dynamic system based on some historical data of that system. A pulse-discharge test was performed on a commercial lithium-ion (Li-ion) battery cell in order to collect data to evaluate those methods. Results are presented and compared.
Keywords:
Artificial neural network (ANN), battery, extended Kalman filter (EKF), state-of-charge (SOC)

1. Introduction
Cost, cycle-life, reliability, and safety are major concerns in all batteries. Due to their high cost in general, batteries must be carefully charged and discharged in order to prolong their cycle-life and thus minimize their maintenance and replacement costs. The battery must also be operated within its design limits to ensure a reliable and safe operation. That is, overcharging batteries produces excessive heat that could damage the battery, shorten its lifetime, and further, result in a fire hazard, where over-discharging batteries could result in an irreversible damage or reduced service-time [1] [2] . Thus, the main function of a battery management system (BMS) is to ensure that the battery operates within its design limits. One important parameter that must be continuously and accurately estimated, under any condition, to prevent the battery from exceeding its design limits is the SOC. Similar to the concept of a fuel gauge, an SOC estimator must provide an accurate value of the amount of energy in the battery as a percentage of its total capacity [3] .
Unlike a fuel gauge, the SOC is an immeasurable quantity that is rather estimated. Nonetheless, there are several methods that can be used to estimate the SOC ranging from simple to sophisticated methods. Those methods can be classified into two types: direct and indirect. Some examples of direct methods include current-integration or “coulomb counting”, which is one of the most common methods used to estimate the SOC. Although current-integration method can be implemented in real-time and can be very accurate, it has one major limitation due to its open-loop nature. That is, with a very small error in the current measurement, the estimated SOC can easily diverge from the true SOC value after few cycles due to accumulated error in the current measurement unless a reset mechanism is periodically used [4] [5] . Another direct method that is used to estimate the SOC is the “open-circuit voltage”. In this method, the voltage is measured continuously and the corresponding SOC is obtained from a lookup table. This method requires a very low (dis)charge current for accurate results, which can be a good choice for some applications that draw very small currents from the battery. Other methods such as the “discharge test” is not practical because it wastes the energy stored in the battery and cannot be used in real-time. In addition, the “impedance spectroscopy” method requires an AC current injection into the cell to measure its impedance and is hard (if not impossible) to achieve dynamically [6] [7] .
On the other hand, there are several indirect methods that are used to estimate the SOC. Those methods can be very accurate and reliable in general. Among those methods are extended Kalman filter (EKF) and artificial neural network (ANN). EKF methods employ advanced battery cell models and require a relatively high computation capability. In contrast, ANN methods don’t rely on any electrical, physical, chemical, or thermal model and they require less computation capability compared to EKF methods. However, ANN methods require huge data to train the network in order to calculate the weight functions for the network [4] [8] . In fact, although many work has been reported on EKF ( [3] [5] [9] - [14] ) and ANN ( [15] - [23] ) SOC estimators, no evaluation nor comparison on those methods has been reported. This paper is an attempt to evaluate the performance of those methods in estimating the SOC through some experimental battery data. Through this paper, the strengths, drawbacks, and capabilities of both EKF- and ANN-based methods in estimating the SOC will be studied, evaluated and compared.
2. Battery Data
To evaluate and compare the capabilities of the presented methods, some battery cell data were gathered from a commercial 1.1 Ah, 3.6 V Li-ion cell. To ensure that the gathered data represent the steady-state and transient battery responses, a pulse-discharge test was performed over the entire capacity range of the cell (from 100% to 0% SOC). In this test, the reference (true) SOC value is obtained by integrating the current with time (coulomb- counting). The battery was fully charged using constant current/constant voltage (CC/CV) profile, then it was discharged using a 1-Amp pulsed current. The pulse and rest durations were set at 6 and 4 minutes, respectively. Since the test comprises only one cycle, the SOC calculated using coulomb-counting is believed to be 100% accurate and thus it will be used later as a reference. The test was performed at room temperature. Since the SOC is strongly dependent on temperature, the test must be repeated at all possible temperatures to evaluate the methods at any temperature. However, the temperature effect is beyond the scope of this paper and thus the methods were evaluated only at room temperature. Also, the calculated SOC in this test and the estimated SOC in the next two sections are found assuming a constant battery total capacity. In order to further generalize the analysis, the test must be performed at different battery conditions, i.e. different battery ageing levels, which also was not considered in this paper. The voltage and SOC are shown in Figure 1.
3. Extended Kalman Filters (EKF)
3.1. Overview
Kalman filter (KF) is an established technique that is used as an optimal estimator to estimate the inner state of a dynamic linear system. For nonlinear systems, a linearized version called extended Kalman filter or EKF is rather used to estimate a system’s state. Basically, KF or EKF is a recursive set of equations that consists of two

Figure 1. Pulse discharge test: (a) Voltage; and (b) SOC.
steps: prediction and correction. In the prediction step, the state of the system is estimated using the previous available measurement, while in the correction step, the estimated state is updated using the current measurement. Figure 2 shows a block diagram of a Kalman filtering process.
3.2. EKF Formulation
If the current is assumed to be positive during charging and negative during discharging, then, the equation of the state-of-charge, 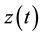 , is given in (1).
, is given in (1).
 (1)
(1)
where 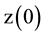 is the initial SOC,
is the initial SOC, 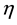 is the charging or discharging efficiency, and
is the charging or discharging efficiency, and 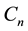 is the nominal capacity,
is the nominal capacity,
which is defined as the number of ampere-hours obtained from a fully charged battery at a 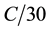 rate at room temperature. In a recursive discrete-time form, the last equation is expressed as in (2).
rate at room temperature. In a recursive discrete-time form, the last equation is expressed as in (2).
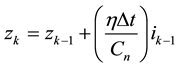 (2)
(2)
To estimate the SOC, an EKF algorithm is constructed as given in the following equations [24] .
・ Firstly, the model is expressed in state-space representation
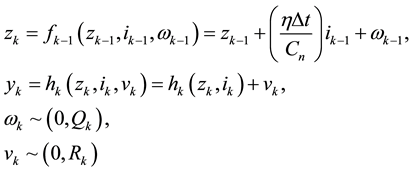
where  is the time index,
is the time index, 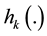 is the output equation of the model,
is the output equation of the model, 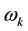 is a discrete-time white noise
is a discrete-time white noise
(process uncertainty) with a covariance matrix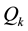 , and
, and 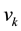 is a discrete-time white noise (measurement uncertainty) with covariance matrix
is a discrete-time white noise (measurement uncertainty) with covariance matrix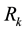 .
.
・ Secondly, the filter is initialized
where 
・ Thirdly, for
1) Compute the following partial derivative matrices:
Figure 2. Kalman filtering process.
2) Perform the time update of the state estimate and estimation error covariance:
3) Compute the following partial derivatives:
4) Measurement update:
3.3. Battery Modeling and SOC Estimation
To accurately estimate the SOC using EKF (the battery is a nonlinear time-variant dynamic system), an accurate battery model must be available. Some existing battery models are briefly presented [25] .
Shepherd Model:

Unnewehr Model:

Nernst Model:

In equations (3)-(5): 







Linear Model: Another battery model is the linear equivalent-circuit model shown in Figure 3. This model simply calculates the battery voltage by adding the voltage drop to the open-circuit voltage (OCV) at a given SOC. The output equation of this model is given in (6).

where 

RC Model: The last battery model discussed in this paper is the RC equivalent-circuit model. This model consists of an RC network as well as an internal resistance as shown in Figure 4. The RC network is added to implement the time constant during transients, which is equivalent in practice to the cell double layer and diffusion capacitance. The equation for this model is given in (7).

where, again, 

In (7), t is the transient time when the cell turns from the charge or discharge state to the idle state and vice versa. For both the linear and RC models, the relationship between the SOC and OCV is found by charging and discharging the cell at a very low current while monitoring the SOC. The OCV-SOC pairs are stored in a lookup table. The exact value of the models’ parameters in equations (3)-(7) that give the least square error can be found using least square estimation [3] . For the RC model, the internal resistance value is the same as that for the linear model. However, the value of the capacitance cannot be found using least square estimation because the relationship between the output voltage and the parameters of the shunt branch (



4. Artificial Neural Networks (ANN)
4.1. Overview
ANN is a subfield of artificial intelligence. It is a mathematical tool that is inspired by the way the human brain processes information [8] . ANNs consist of a number of layers each of which consists of a number of processing units called “neurons” as the basic unit. The neurons are interconnected through weight functions as shown in Figure 6(a). Figure 6(b) shows a block diagram of an adaptive ANNs operation.
ANNs are highly stable and robust due to their massive parallel structure. ANNs consist of inputs and outputs and are made of neurons interconnected with each other. The weights in Figure 7 are determined during the training phase and their values determine how the neural network will respond to a particular time series of inputs. Thus, training ANNs is the most critical phase that determines how accurate those ANNs are. One thing to mention is that ANNs can have an open-loop (feed-forward) or closed-loop (feed-back) structure. Another important feature of ANNs is their ability to adapt to changes (this kind of neural networks is called adaptive artificial neural network). The weights in adaptive ANNs continuously adapt, in real-time, to changes that occurs after training, while non-adaptive ANNs have fixed weights that are determined in the training phase.
The weights of an ANN are calculated in the training phase by minimizing the loss function (usually a quadratic function of the output error). One common technique that is widely used in training ANNs is the back-propagation, which is a supervised learning method that is commonly used in the training phase to calcu-
Figure 3. Linear equivalent-circuit model.
Figure 4. RC equivalent-circuit model.

Figure 5. (a) Results of voltage prediction for the presented models; (b) Results of estimating the SOC using EKF for the presented models.

Figure 6. (a) A two-layer feed-forward ANN with 10 hidden neurons, n input neurons and 1 output neuron; (b) Operational block diagram of ANN.
Figure 7. A non-linear input-output (NIO) feed-forward ANN with d time delays.
late the weights of a neural network. Back-propagation uses a steepest-descent technique based on the computation of the gradient of the loss function with respect to the network parameters [26] .
4.2. SOC Estimation
To evaluate the performance of ANNs in estimating the SOC, two common network architectures were selected: the first is nonlinear input-output (NIO) feed-forward network, and the second is nonlinear autoregressive with exogenous input (NARX) feed-back network. For both networks, Levenberg-Marquardt back-propagation algorithm was used in training.
NIO feed-forward network predicts one time series given the current and past values of an input time series as shown in Figure 7. For the purpose of estimating the SOC, the input time series x(t) consists of the battery terminal voltage and current, where the output or target is the SOC.
The output equation of this network is given in (8).

NARX feed-back network, on the other hand, predicts one time series given the current and past values of an input time series as well as the past and current values of another time series, called external or exogenous time series (output). A block diagram of this network is shown on Figure 8.
The output equation of this network is given in (9).

In (8) and (9): 




For both networks, the delay parameter indicates the delay in the input/output time series and it can be selected by trial and error until the desired accuracy is obtained. The number of neurons in the hidden layer was set at 10. The value of the delay parameter and the number of neurons in the hidden layer were purposefully varied in order to find the effect of the selected values on the network performance.
The results of estimating the SOC for both the NIO and NARX models are shown in Figure 9. The value of the delay parameter 
5. Comparative Summary of Results
In order to obtain practical results, a zero-mean process noise with an absolute peak value of 10 mA and a zero-mean measurement noise with an absolute peak value of 10 mV were added to the current and voltage readings. The results in Figure 5 and Figure 9 are obtained after the process and measurement were contaminated. Both the process and measurement noises are independent and Gaussian. The presented methods are evaluated and compared in the rest of this section.
It is obvious in Figure 5(b) that the accuracy of the EKF algorithms is totally dependent on the accuracy of the model. Actually, this total dependence of EKFs on the adopted model is problematic and can result in inaccurate and instable performance when estimating the battery SOC. In other words, a small mismatch between the model voltage and the true voltage can lead the estimated SOC to diverge from the true SOC. In the presented EKF algorithms, Nernst model performed better than Shepherd and Unnewehr models because it employs two correction factors. The linear and RC equivalent circuit models performed much better than Shepherd, Un-
Figure 8. A non-linear autoregressive with exogenous input (NARX) feed- back ANN with d time delays.

Figure 9. Results of estimating the SOC with delay values equal 2, 4, 6, 8 and 10 using (a) NIO feed-forwardANN, and (b) NARX feed-back ANN.
newehr and Nernst models because they are more advanced since they use an OCV-SOC lookup table. The RC model outperformed all the other models because it handles both the internal voltage drop and transient (capacitance) voltage of the battery.
In fact, one advantage of EKFs is that they can still be accurate even if the initial guess was incorrect. To verify that, the initial SOC was purposefully changed from 100% (true value) to 80% (wrong value), and it was noticed that every time the algorithm converged to the true value after a relatively short time (within 5 minutes). Another advantage of EKFs is that they can also provide accurate performance even when the process and measurement have noise. To verify this, a white noise (Gaussian) was added to both the current and voltage. All the EKF algorithms, regardless what battery model they used, were able to achieve almost the same results before the process and measurement were contaminated.
In practice, however, the process and measurement noise is not necessarily white. If so, conventional EKFs will not perform well. Thus, EKFs can be a good option only and only if an accurate battery and noise models are used; otherwise, EKFs will not be accurate and will be prone to stability issues.
On the other hand, the presented ANNs showed different performances. NARX networks obviously outperformed NIO networks due to their feedback loop. In the presented NARX network, the feedback loop was used in the training phase to calculate the weight functions. The feedback resulted in a more accurate performance as can be seen by comparing the NARX and NIO models. However, although the calculated weight functions for both the NIO and NARX models are optimal in the sense that they gave the best possible performance, the weight functions must be able to adapt to changes in the ambient conditions or battery parameters.
One remark on the presented ANNs is the relationship between the delay parameter 


Table 1. Evaluation of reviewed methods in terms of RMSE and linear regression.
choice when no output data is available. It was shown that as 
Another remark on the ANNs models is that there was almost no relationship between the network accuracy and the number of neurons in the hidden layer. It was noticed that when the number of neurons in the hidden layer is less than 5, the accuracy is slightly lower than when the number of neurons is above 5. However, the performance of the network didn’t change at all when the number of neurons in the hidden layer was changed randomly between 5 and 100 for both NIO and NARX networks.
To quantitatively compare the presented methods, the root mean square error (RMSE) and regression were calculated and summarized in Table 1.
The regression in Table 1 was found using MATLAB function (plotregression), where the RMSE was found using equation (10).

where 


6. Conclusion
Two advanced SOC estimation methods were analyzed, compared and evaluated. The two methods, EKFs and ANNs, can perform well under certain conditions. That is, EKFs can perform well if an accurate battery and noise models are used, where ANNs can perform well if they were trained with an artificial experience (training) that is very close or identical to the real experience. However, even with ideal battery model or training, the actual EKF or ANN SOC estimator will not be ideal due to the variation between battery cells in their internal parameters even if they were from the same manufacturer. Other factors that must be taken into account when designing an SOC estimator are the dependence of the battery on temperature and the change in the battery parameters (i.e. capacity, internal resistance, etc.) through the battery lifetime. Thus, adaptability is a key issue for highly reliable SOC estimators through the battery lifetime.
Acknowledgements
This research was supported in part by the United Arab Emirates University under startup research grant # G00001287.
References
- Cope, R.C. and Podrazhansky, Y. (1999) The Art of Battery Charging. The 14th Annual IEEE Battery Conference on Applications and Advances, Long Beach, 12-15 January 1999, 233-235.
- Hussein, A.A. and Batarseh, I. (2011) A Review of Charging Algorithms for Nickel and Lithium Battery Chargers. IEEE Transactions on Vehicular Technology, 60, 830-838. http://dx.doi.org/10.1109/TVT.2011.2106527
- Hussein, A.A. and Batarseh, I. (2011) State-of-Charge Estimation for a Single Lithium Battery Cell Using Extended Kalman Filter. IEEE Power and Energy Society General Meeting, 24-29 July 2011, San Diego, 1-5.
- Hussein, A.A. (2013) Capacity Fade Estimation in Electric Vehicles Li-Ion Batteries Using Artificial Neural Networks. 2013 ECCE Conference, Denver, 15-19 September 2013, 677-681.
- Plett, G.L. (2004) Extended Kalman Filtering for Battery Management Systems of LiPB-Based HEV Battery Packs: Part 3. State and Parameter Estimation. Journal of Power Sources, 134, 277-292. http://dx.doi.org/10.1016/j.jpowsour.2004.02.033
- Piller, S., Perrin, M. and Jossen, A. (2001) Methods for State-of-Charge Determination and Their Applications. Journal of Power Sources, 96, 113-120. http://dx.doi.org/10.1016/S0378-7753(01)00560-2
- Hussein, A.A., Kutkut, N., Shen, J. and Batarseh, I. (2012) Distributed Battery Micro-Storage Systems Design and Operation in a Deregulated Electricity Market. IEEE Transactions on Sustainable Energy, 3, 545-556. http://dx.doi.org/10.1109/TSTE.2012.2191806
- Haykin, S. (1999) Neural Networks and Learning Machines. 3rd Edition, 1-46.
- He, H., Xiong, R., Zhang, X. and Sun, F. (2011) State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Transactions on Vehicular Technology, 60, 1461-1469. http://dx.doi.org/10.1109/TVT.2011.2132812
- Zhang, F., Guangjun, L. and Fang, L. (2008) A Battery State of Charge Estimation Method with Extended Kalman Filter. IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Xian, 2-5 July 2008, 1008-1013. http://dx.doi.org/10.1109/AIM.2008.4601799
- Qiu, S., Chen, Z., Masrur, M.A. and Murphey, Y.L. (2011) Battery Hysteresis Modeling for State of Charge Estimation Based on Extended Kalman Filter. Proceedings of the 6th IEEE Conference on Industrial Electronics and Applications, Beijing, 21-23 June 2011, 184-189.
- Domenico, D.D., Fiengo, G. and Stefanopoulou, A. (2008) Lithium-Ion Battery State of Charge Estimation with a Kalman Filter Based on a Electrochemical Model. Proceedings of the IEEE International Conference on Control Applications, San Antonio, 3-5 September 2008, 702-707.
- Yan, W., Ming, Y.T. and Jie, L.B. (2008) Lead-Acid Power Battery Management System Basing on Kalman Filtering. Proceedings of the IEEE Vehicle Power and Propulsion Conference, Harbin, 3-5 September 2008, 1-6.
- Windarko, N.A., Choi, J. and Chung, G.B. (2011) SOC Estimation of LiPB Batteries Using Extended Kalman Filter Based on High Accuracy Electrical Model. Proceedings of the 8th IEEE International Conference on Power Electronics and ECCE Asia, Jeju, 30 May-3 June 2011, 2015-2022. http://dx.doi.org/10.1109/ICPE.2011.5944483
- Chan, C.C., Lo, E.W.C. and Weixiang, S. (2000) The Available Capacity Computation Model Based on Artificial Neural Network for Lead-Acid Batteries in Electric Vehicles. Journal of Power Sources, 87, 201-204. http://dx.doi.org/10.1016/S0378-7753(99)00502-9
- Shi, P., Bu, C. and Zhao, Y. (2005) The ANN Models for SOC/BRC Estimation of Li-Ion Battery. Proceedings of the IEEE International Conference on Information Acquisition, Hong Kong and Macau, 27 June-3 July 2005.
- Shen, W.X., Chan, C.C., Lo, E.W.C. and Chau, K.T. (2002) A New Battery Available Capacity Indicator for Electric Vehicles Using Neural Network. Energy Conversion and Management, 43, 817-826. http://dx.doi.org/10.1016/S0196-8904(01)00078-4
- Yamazaki, T., Sakurai, K. and Muramoto, K. (1998) Estimation of the Residual Capacity of Sealed Lead-Acid Batteries by Neural Network. Proceedings of the 20th International Telecommunications Energy Conference, San Francisco, 4-8 October 1998, 210-214.
- Affanni, A., Bellini, A., Concari, C. and Franceschini, G. (2003) EV Battery State of Charge: Neural Network Based Estimation. Proceedings of the IEEE International Electric Machines and Drives Conference, Madison, 1-4 June 2003, 684-688. http://dx.doi.org/10.1109/IEMDC.2003.1210310
- Shen, W.X. (2007) State of Available Capacity Estimation for Lead-Acid Batteries in Electric Vehicles Using Neural Network. Energy Conversion and Management, 48, 433-442. http://dx.doi.org/10.1016/j.enconman.2006.06.023
- Shen, W.X., Chau, K.T., Chan, C.C. and Lo, E.W.C. (2005) Neural Network-Based Residual Capacity Indicator for Nickel-Metal Hydride Batteries in Electric Vehicles. IEEE Transactions on Vehicular Technology, 54, 1705-1712. http://dx.doi.org/10.1109/TVT.2005.853448
- Cai, C.H., Du, D., Liu, Z.Y. and Zhang, H. (2002) Artificial Neural Network in Estimation of Battery State of Charge (SOC) with Nonconventional Input Variables Selected by Correlation Analysis. Proceedings of the International Conference on Machine Learning and Cybernetics, Beijing, 4-5 November 2002, 1619-1625.
- Chen, Z., Qiu, S., Masrur, M.A. and Murphey, Y.L. (2011) Battery State of Charge Estimation Based on a Combined Model of Extended Kalman Filter and Neural Networks. Proceedings of the 2011 International Joint Conference on Neural Networks (IJCNN), San Jose, 31 July-5 August 2011, 2156-2163. http://dx.doi.org/10.1109/IJCNN.2011.6033495
- Simon, D. (2006) Optimal State Estimation. Wiley-Interscience, Hoboken, 407-409.
- Hussein, A.A. and Batarseh, I. (2011) An Overview of Generic Battery Models. Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, 24-29 July 2011, 1-6.
- Hippert, H.S., Pedreira, C.E. and Souza, R.C. (2001) Neural Networks for Short-Term Load Forecasting: A Review and Evaluation. IEEE Transactions on Power Systems, 16, 44-55. http://dx.doi.org/10.1109/59.910780

















