International Journal of Modern Nonlinear Theory and Application
Vol.03 No.04(2014), Article ID:49911,13 pages
10.4236/ijmnta.2014.34017
Nonlinear Control of Bioprocess Using Feedback Linearization, Backstepping, and Luenberger Observers
Muhammad Rizwan S. Khan, Robert N. K. Loh
Department of Electrical and Computer Engineering, Oakland University, Rochester, Michigan, USA
Email: mskhan@oakland.edu, loh@oakland.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 July 2014; revised 15 August 2014; accepted 29 August 2014
ABSTRACT
This paper addresses the analysis, design, and application of observer-based nonlinear controls by combining feedback linearization (FBL) and backstepping (BS) techniques with Luenberger observers. Complete development of observer-based controls is presented for a bioprocess. Controllers using input-output feedback linearization and backstepping techniques are designed first, assuming that all states are available for feedback. Next, the construction of observer in the transformed domain is presented based on input-output feedback linearization. This approach is then extended to observer design based on backstepping approach using the error equation resulted from the backstepping design procedure. Simulation results demonstrating the effectiveness of the techniques developed are presented and compared.
Keywords:
Bioprocess, Feedback Linearization, Backstepping, Luenberger Observers, Observer-Based Control

1. Introduction
In process control, a major difficulty is to provide direct real-time measurements of the state variables required to implement advanced monitoring and control methods on bioreactors [1] -[5] . Dissolved oxygen concentration in bioreactors, temperature in non-isothermal reactors and gaseous flow rates, are available for on-line measurement while the values of concentration of products, reactants and/or biomass are often available only via on-line analysis [2] - [4] , which means that these variables are not available for real-time feedback control. An alternative is to use state observers which, in conjunction with the process model and available measurements, can generate accurate estimates of the unmeasured and/or inaccessible states effectively. Exponential and asym- ptotic observers and their variants to estimate unmeasured states in bioprocess systems have appeared in [1] - [5] . In [6] , Dochain and Perrier applied backstepping [7] - [9] , techniques to the nonlinear control of microbial growth problem in a CSTR (continuously stirred tank reactor) and two controllers were proposed. The first one was a non-adaptive version, while the second one was an adaptive version in which the maximum specific growth rate was estimated on-line. However, backstepping-based observer design was not considered in [6] .
In this paper, a complete development of observer-based control is presented that includes feedback linearization [7] [8] [10] [11] , backstepping [7] - [9] , Luenberger observer [12] with feedback linearization, and Luenberger observer with backstepping.
The paper is organized as follows. Section 2 presents the bioprocess model for control design. Theoretical foundation of input-output feedback linearization (FBL) and controller design are outlined in Section 3 with simulation results. Section 4 addresses the formulation and application of backstepping (BS) control with simulation results. In Section 5, simulation results are compared for both approaches, i.e., FBL and BS. Section 6 addresses the design of Luenberger observers for FBL and BS controls with simulations. The conclusions are presented in Section 7.
2. Bioprocess Model
The model dynamics in a CSTR (continuous stirred tank reactor) with a simple microbial growth reaction, with one substrate  and biomass
and biomass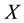 , are given by the following equations [1] :
, are given by the following equations [1] :
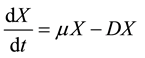 , (1)
, (1)
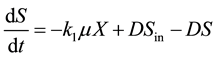 , (2)
, (2)
where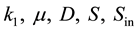 , represent the yield coefficient, specific growth rate (h−1), dilution rate (h−1), and substrate concentration (grams/lit) in the influent and reactor, respectively.
, represent the yield coefficient, specific growth rate (h−1), dilution rate (h−1), and substrate concentration (grams/lit) in the influent and reactor, respectively.
The biomass concentration 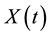 (grams/lit) is the variable which is to be controlled. Defining the parameter
(grams/lit) is the variable which is to be controlled. Defining the parameter  as
as 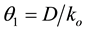 and expressing specific growth rate
and expressing specific growth rate 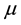 as
as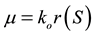 , the dynamical Equations (1) and (2) above can be written as [6]
, the dynamical Equations (1) and (2) above can be written as [6]
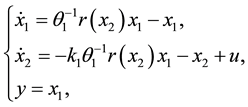 (3)
(3)
where it is assumed that the biomass concentration 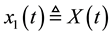 can be measured with a sensor, i.e., the output is given by
can be measured with a sensor, i.e., the output is given by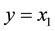 , while
, while 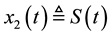 denotes the substrate concentration and
denotes the substrate concentration and 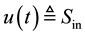 is the control input. The bioprocess model given by (3) can be written compactly in an alternate state-space form as:
is the control input. The bioprocess model given by (3) can be written compactly in an alternate state-space form as:
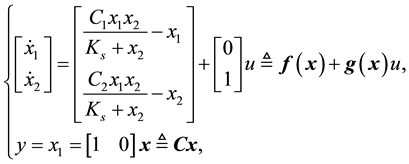 (4)
(4)
where 
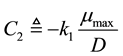

tion kinetics, which can expressed as
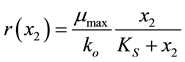
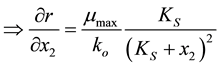
We will use (3) for back stepping control and observer design and (4) will be utilized for developing the control law and observer design using the feedback linearization approach. Typical values of the model parameters needed for the simulation studies are given in Table 1 [6] .
3. Feedback Linearization (FBL) Control Design
The main intent of this section is to investigate control design using the input-output feedback linearization (FBL) technique. Consider a general nonlinear control-affine SISO system described by [7] [8] [10] [11] ,
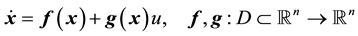

where 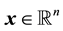
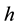
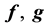
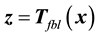
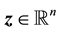
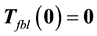
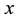
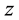
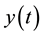
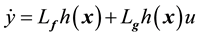
where 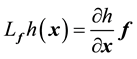

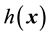
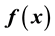
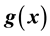
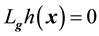
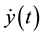
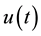
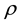
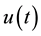
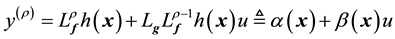
where 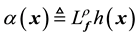

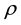
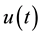
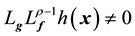
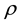
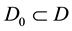
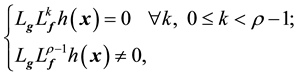
for all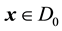
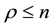
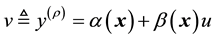
where 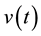
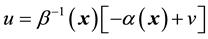
Table 1. Parameter data.
provided 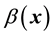
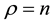
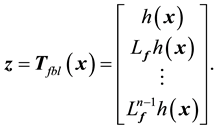
If ρ < n, the diffeomorphism Tfbl(x) comprises of both external and internal dynamics, i.e., 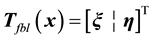
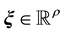

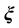

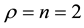
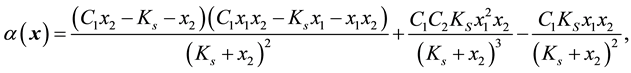
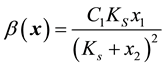
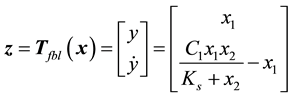
where 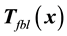

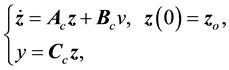
where
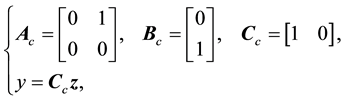
and 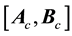
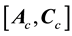
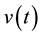
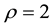

where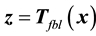
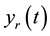
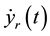
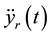
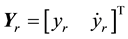
and the constant feedback gain matrix 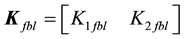
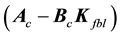
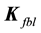
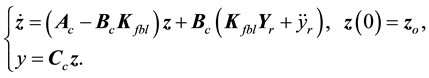
The linearizing feedback control law in the 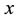
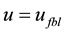
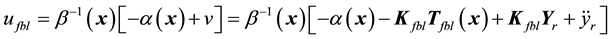
which yields the closed-loop system
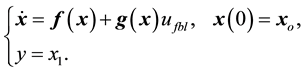
The design of a PP control law (20) for the 2nd-order system (18) is achieved by choosing a damping ratio 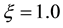

loop poles are given by 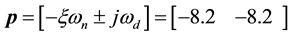
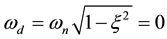
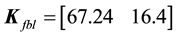
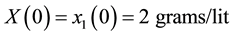
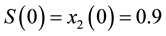
4. Backstepping (BS) Control Design
We shall address the design of back stepping (BS) [7] -[9] control in this section, where the parameter 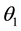
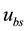

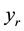

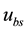
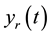
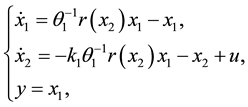
where 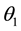

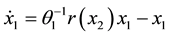
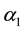
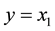
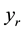
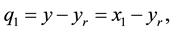
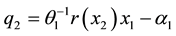
Figure 1. Responses of closed-loop bioprocess (23) under FBL control 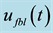
where 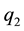
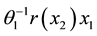
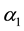
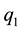
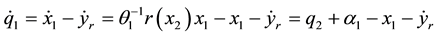
Consider the Lyapunov function candidate
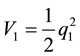
which yields the derivative, with (26),

Choosing the stabilizing function 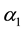
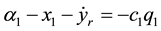
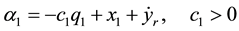
Substituting (29) into (26) and (28) yields, respectively,

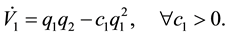
From (31), if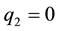
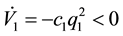
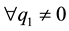
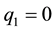
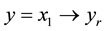

The next step is to develop a BS control law for
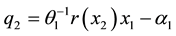
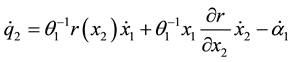
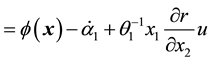
where

and 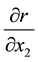
To stabilize the 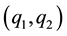
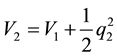
The derivative of 
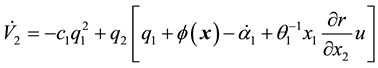
Defining 

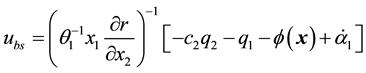
Substituting (37) into (33) and (36), we obtain,
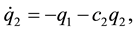
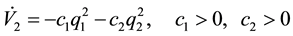
Since 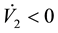
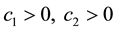

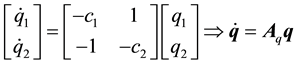
Since 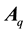
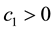
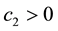

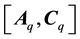

Meanwhile, the closed-loop bioprocess under BS control is given by,
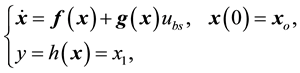
where 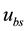
Simulation studies were conducted using (41) with the backstepping gains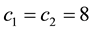
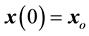
5. Comparison of FBL and BS Designs
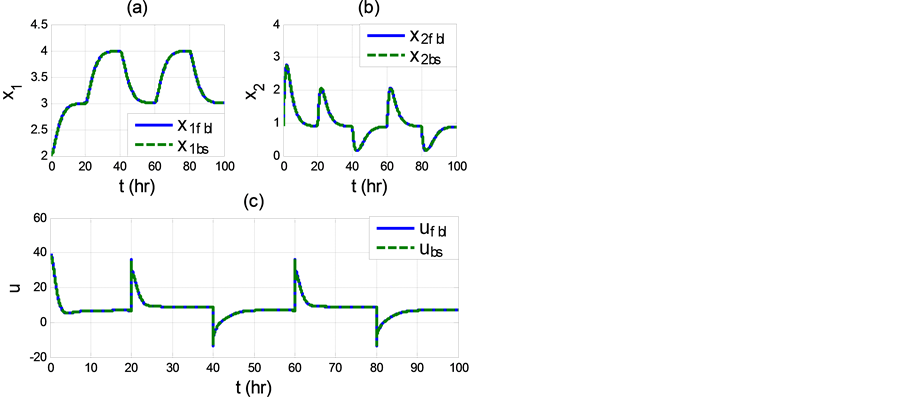
The simulation results for the FBL versus BS designs using the gains reported in Sections 3 and 4 are shown in Figure 3 and Figure 4 for comparison purposes.
It can be seen that both 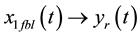
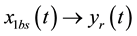
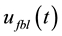
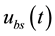
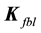
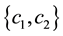
6. Observer-Based FBL and BS Controls
As mentioned before that not all state variables are measured in the bioreactor systems; therefore, suitable observers are needed for realizing the full-state feedback control designs proposed in Sections 3 and 4. We shall
Figure 2. Responses of closed-loop bioprocess (41) under BS control 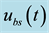
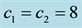
Figure 3. Comparing FBL responses in Figure 1 and BS responses in Figure 2.
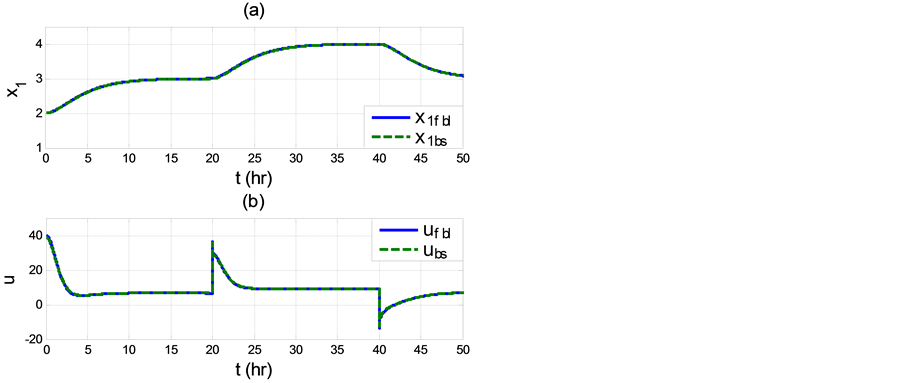
Figure 4. Zoomed-in view of 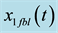
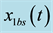

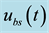
investigate the constructions of Luenberger observers for the FBL-based and BS-based control approaches in this section
6.1. Luenberger Observer for FBL Control
Since only 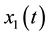
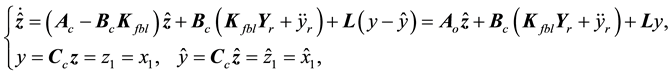
where 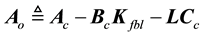


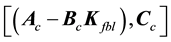

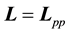


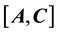
observable pair, the pair 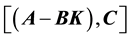
servability; furthermore, 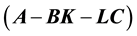

Now using (21) and (42), it can readily be shown that the estimation error 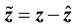

where the initial condition 
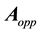
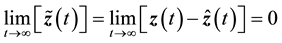
for all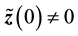
Using the transformation defined by (17), the observer described by (42) in the 
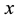
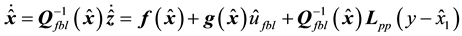
where 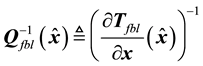
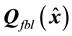
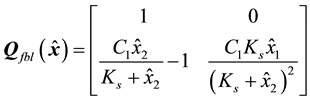
In summary, the observer-based control system with feedback linearization for the bioprocess under consideration has the form
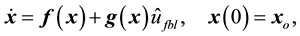
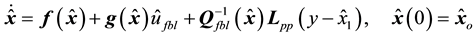
where 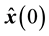
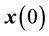
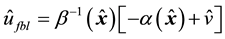
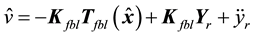
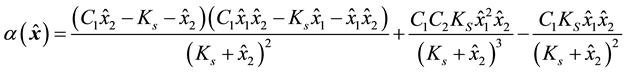
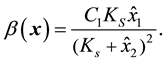
6.2. Luenberger Observer for BS Control
In this section we pursue our final objective, i.e., to design a Luenberger observer based on the BS formulation using the error Equation (40). To construct an observer for (40), we need an output equation which can be defined as,
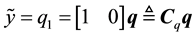
where 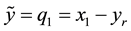

We present the following proposition.
Proposition 1
Consider the bioprocess system described by (3) and (4). A Luenberger observer for the associated error system (40) with measurement given by (53) can be constructed as
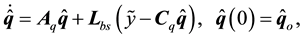
where 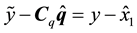
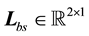

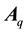
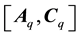
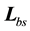

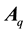
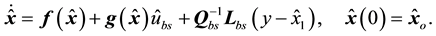
Proof: First, we need to show that the estimate 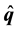
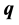


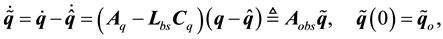
where 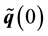
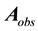
for arbitrary 
Equation (58) yields the Jacobian matrix
where 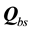
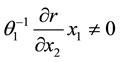
tions (58) and (59) yield 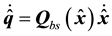
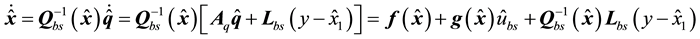
where 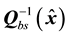
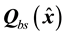

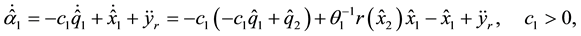
which complete the proof.
The observer design technique developed here is interesting and attractive and is different from the two-filter approach in [9] . The technique can be applied to a wide class of BS-based error systems.
In summary, the observer-based control system with the BS formulation for the bioprocess is described by
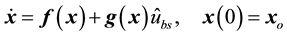
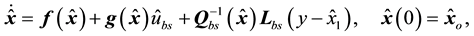
where 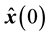
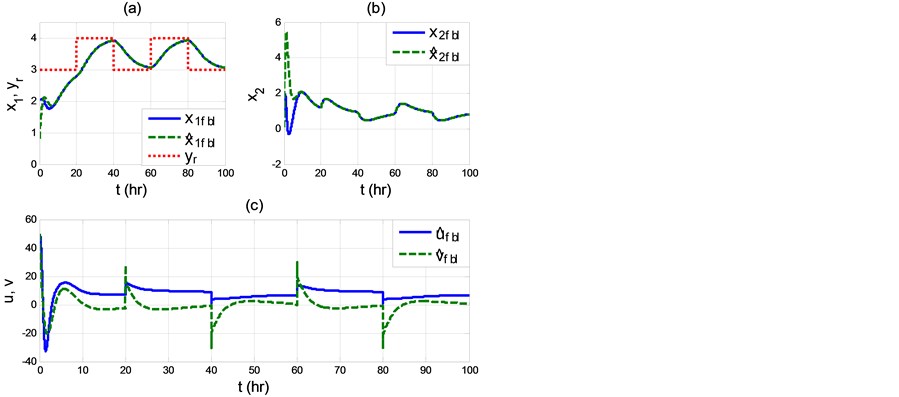
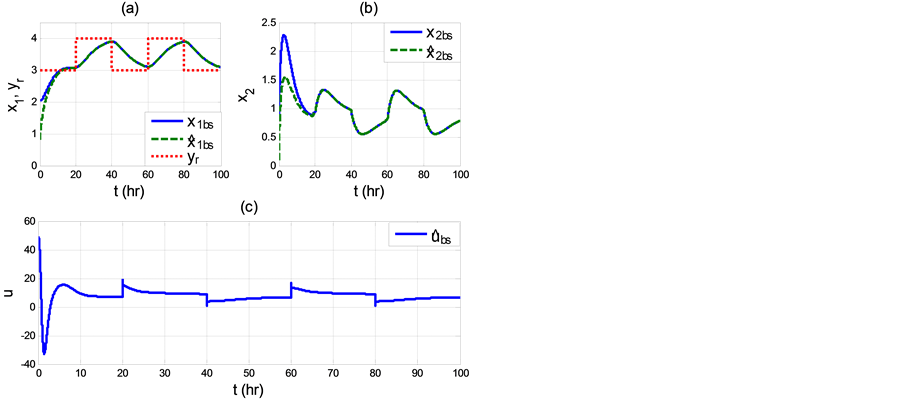
Simulation studies for the proposed observer-based FBL and BS controls were conducted and compared. The initial conditions were chosen as 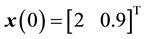
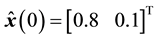
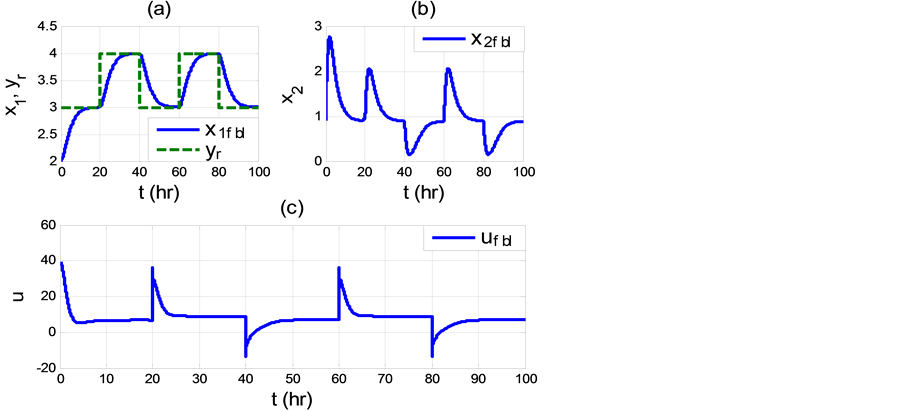
In Figure 5, results for observer-based FBL control scheme described by (47) and (48) are shown. It can be seen that the estimates 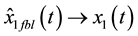
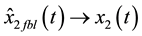
In Figure 7, the behavior of the error variables 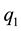

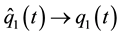
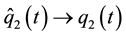
7. Conclusion
Observers are critical to control system analysis and designs that employ full-state feedback, where not all the state variables are accessible for on-line, real-time measurements, and/or where the measurements are corrupted by noise. Indeed, the design of suitable linear or nonlinear observers or filters leading to observer-based control technology is an integral part of real world control system applications. In this paper, observer-based control strategies were developed for a nonlinear bioprocess system using feedback linearization and backstepping control techniques; in particular, a Luenberger observer for backstepping control was formulated using the error equation resulted from the backstepping design procedure. The observer design technique developed here is interesting and attractive and is different from the two-filter approach known in the literature. Simulation results with and without observers for both the FBL and BS schemes are presented and compared. The results were excellent and demonstrated the feasibility and effectiveness of the proposed approaches.
Table 2. Controllers and observer gains.
Figure 5. Responses of observer-based FBL control scheme (47) and (48): 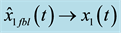
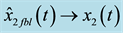
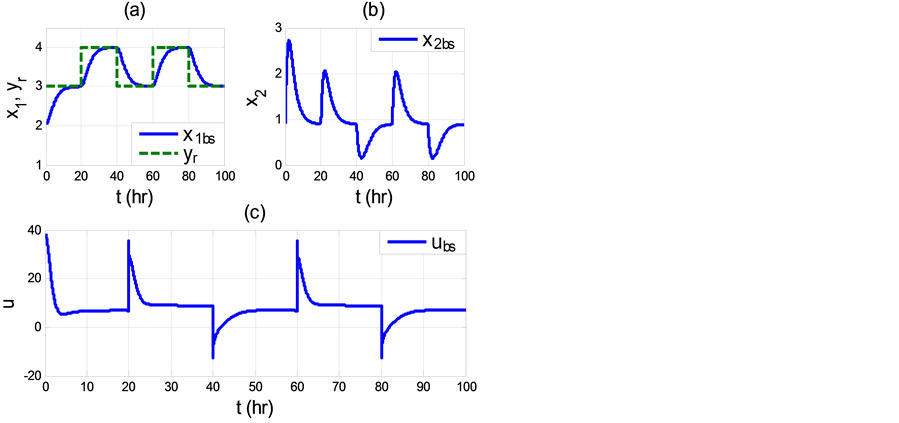
Figure 6. Responses of observer-based BS control scheme (63) and (64): 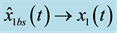

Figure 7. Evolution of the backstepping error variables: 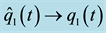
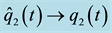
Acknowledgements
The authors would like to thank all the reviewers for their feedbacks and constructive criticisms.
Cite this paper
Muhammad Rizwan S.Khan,Robert N. K.Loh, (2014) Nonlinear Control of Bioprocess Using Feedback Linearization, Backstepping, and Luenberger Observers. International Journal of Modern Nonlinear Theory and Application,03,150-162. doi: 10.4236/ijmnta.2014.34017
References
- 1. Bastin, G. and Dochain, D. (1990) On-line Estimation and Adaptive Control of Bioreactors. Elsevier, Amsterdam.
- 2. Dochain, D. (2003) State and Parameter Estimation in Chemical and Biochemical Processes: A Tutorial. Journal of Process Control, 13, 801-818. http://dx.doi.org/10.1016/S0959-1524(03)00026-X
- 3. Dochain, D. and Rapaport, A. (2005) Internal Observers for Biochemical Processes with Uncertain Kinetics and Inputs. Mathematical Biosciences, 193, 235-253. http://dx.doi.org/10.1016/j.mbs.2004.07.004
- 4. Dochain, D. (2000) State Observers for Tubular Reactors with Unknown Kinetics. Journal of Process Control, 10, 259-268. http://dx.doi.org/10.1016/S0959-1524(99)00020-7
- 5. Hulhoven, X., Vande Wouwer, A. and Bogaerts, Ph. (2006) Hybrid Extended Luenberger-Asymptotic Observer for Bioprocess State Estimation. Chemical Engineering Science, 61, 7151-7160.
http://dx.doi.org/10.1016/j.ces.2006.06.018 - 6. Dochain, D. and Perrier, M. (2003) Adaptive Backstepping Nonlinear Control of Bioprocesses. International Federation of Automatic Control Proceedings, ADCHEM, 77-82.
- 7. Khalil, H.K. (2002) Nonlinear Systems. 3rd Edition, Prentice Hall, Upper Saddle River.
- 8. Marquez, H.J. (2003) Nonlinear Control Systems: Analysis and Design. John Wiley & Sons, Hoboken.
- 9. Krstic, M., Kanellakopoulos, I. and Kokotovic, P. (1995) Nonlinear and Adaptive Control Design. John Wiley, New York.
- 10. Isidori, A. (1995) Nonlinear Control Systems. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-1-84628-615-5 - 11. Krener, A.J. (1999) Feedback Linearization. In: Baillieul, J. and Willems, J.C., Eds. Mathematical Control Theory, Chapter 3, Springer-Verlag, New York, 66-98.
- 12. Luenberger, D.G. (1964) Observing the State of a Linear System. IEEE Transactions on Military Electronics, 8, 74-80.
http://dx.doi.org/10.1109/TME.1964.4323124 - 13. Kalman, R.E. and Bucy, R.S. (1961) New Results in Linear Filtering and Prediction Theory. Transactions of the ASME, 83D, 429-438.
- 14. Ogata, K. (2010) Modern Control Systems. 5th Edition, Prentice Hall, Upper Saddle River.
- 15. Dorf, R. and Bishop, R. (2008) Modern Control Systems. 11th Edition, Pearson Education, Upper Saddle River.