Received 21 March 2014; revised 21 April 2014; accepted 26 April 2014

ABSTRACT

In the paper, several different methods are adopted to control Lü system. With direct feedback method, Lü system can be stabilized at one equilibrium point or a limit cycle surrounding its equilibrium. With adaptive time-delayed feedback method, feedback coefficient and delay time can be adjusted adaptively to stabilize Lü system at its original unstable periodic orbit. With minimal energy method, Lü system can also be stabilized at fixed point or limit cycle. Numerical simulations show the effectiveness of our methods.

Keywords:

Lü System, Direct Feedback, Adaptive Time-Delayed Feedback, Minimal Energy Method

1. Introduction

In 1990, Ott, Grebogi and Yorke presented the OGY method to control chaos [1] . After their pioneering work, chaotic control has become a focus in nonlinear problems and a lot of work has been done in the field [2] -[4] . Nowadays, many methods have been proposed to control chaos [5] [6] . Generally speaking, there are two kinds of control ways: feedback control and nonfeedback control [7] -[14] . Feedback methods are used to stabilize the unstable periodic orbit of chaotic systems by feeding back their states. Nonfeedback methods are adopted to change chaotic behaviors by applying perturbations to some parameters or variables. In the paper, we use several different methods to control the dynamic behavior of Lü system. With direct feedback method, Lü system can be stabilized at equilibrium point or limit cycle around its equilibrium. With adaptive time-delayed feedback method, Lü system can be stabilized at its original unstable periodic orbit. With minimal energy method (it’s a nonfeedback method), Lü system can also be stabilized at fixed point or limit cycle, though the fixed point or the center of the limit cycle is not its original equilibrium. Numerical simulations show the effectiveness of these methods.

2. The Description of Lü System

The unified chaotic system [15] is described as

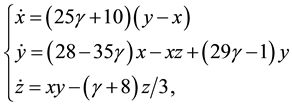(1)

where. When, system (1) belongs to Lorenz chaotic system [16] ; when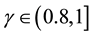, system (1) belongs to Chen chaotic system [17] ; when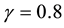, system (1) belongs to Lü chaotic system [18] .

Obviously, Lü system is a bridge between Lorenz system and Chen system, so the study of Lü system is very significant. Let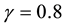, then system (1) is described as

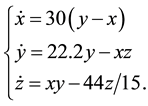(2)

System (2) is a typical Lü system. The attractor is shown in Figure 1 and the relevant projections of this attractor are shown in Figure 2.

There are close relationships between system (2) and a large class of chaotic systems (i.e. generalized Lorenz system family [19] ), so it’s very meaningful to study the chaotic control of system (2). Next, direct feedback method, adaptive time-delayed feedback method and minimal energy method will be adopted to control this typical Lü system respectively.

3. The Chaotic Control of Lü System with Three Methods

3.1. Direct Feedback Method

System (2) has three equilibriums, i.e., 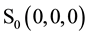, and.

Suppose we want to stabilize Lü system at equilibrium S₁ and the limit cycle surrounding S₁ respectively. For convenience, choose y as feedback variable, this feedback is added to the second function of Equation (2), then the controlled Lü system can be described as

(3)

where k is feedback coefficient. The Jacobian matrix of system (3) at 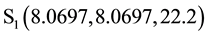is

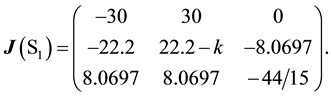(4)

Suppose 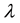as eigenvalue, then the characteristic equation of Equation (4) is

, (5)

where, ,.

According to Routh-Hurwitz criterion, when, , and, the real parts of all the eigenvalues of Equation (4) are negative, then system (3) will be stabilized at. It’s easy to obtain the solution. Choose, the numerical simulations of system (3) are shown in Figure 3.

Choose the critical value, the eigenvalues of Equation (4) are 16.4365j, −16.4365j and −16.2644, system (3) is a limit cycle surrounding S₁, the numerical simulations are shown in Figure 4.

In the same way, Lü system can be stabilized at S₀ or S₂, or the relevant limit cycle surrounding S₀ or S₂. From numerical simulations, we see that Lü system may exhibit periodic behavior with the direct feedback method, but the profile of the original chaotic Lü attractor disappears under this control method. Next, an adaptive

time delayed feedback method will be adopted to control Lü system, and the periodic orbit of the controlled system can maintain the profile of the original Lü attractor.

3.2. Adaptive Time-Delayed Feedback Method

In the time-delayed feedback method, the feedback signal can be described as [20]

, (6)

where K is feedback coefficient; is delay time; X is measurable variable. In practical applications, it’s important to choose proper K and. K and can be obtained by experiments and calculation. Pyragas has discussed about how to choose K and detailedly [20] . As for non-autonomous system, we can choose the period of external force as; As for autonomous system, the calculation of K and is very tedious. Many numerical calculation results show that the available range of K is very small and it’s not easy to obtain the optimal solution of K. Though people have done a lot of work [21] -[23] in this field, how to find available K and quickly and effectively is still an unresolved problem.

In the paper, we choose an adaptive algorithm to obtain proper feedback coefficient K and delay time. Suppose the controlled Lü system as

(7)

where the controller, then we can realize dynamic regulation of feedback coefficient k and delay time by the following algorithm.

As for feedback coefficient k, let, where weight coefficient, obviously k can be dynamically adjusted by the error; as for delay time, we choose as the time interval between two adjacent maximum of z, i.e., where means z reaches its nth maximum at.

In numerical simulations, choose time step 0.001 second, let initial state and, the attractor of system (7) is shown in Figure 5, the projections of system (7)’s attractor are shown in Figure 6. From Figure 5 and Figure 6, we can see that Lü system has been stabilized at its original unstable periodic orbit successfully.

The simulation results of feedback coefficient k and delay time are shown in Figure 7(a) and Figure 7(c). Figure 7(b) is part of Figure 7(a) with time from 45 sec to 60 sec. The simulation results of x, y, z with time from 45 sec to 60 sec are shown in Figure 8. From these simulation results, we can know that becomes stable at 0.365 second lastly; the period of z is, and the period of x and y is, so the period of system (7) is. Generally speaking, feedback coefficient is a constant, while in this paper, the coefficient k changes periodically under the adaptive time-delayed feedback control, which shows that when the period of feedback coefficient equals that of the controlled system, chaotic control may also be realized.

3.3. Minimal Energy Method

For physical systems, less energy means more stability, so reducing energy is an effective method to control

chaos. Generally speaking, when the energy of a chaotic system is reduced to a critical value, the system may behave period. According to this idea, we can design a strategy to stabilize Lü system at periodic orbits. For a chaotic system, it’s not easy to calculate its energy, but a generalized energy function can be used to instead of true energy. In many cases, Lyapunov function can be seemed as a generalized energy function. By calculation, the average energy can be obtain (is the average value of the Lyapunov function), then we can choose, adjust some variable(s) of this system so that the energy is no more than. Choose proper, then the controlled chaotic system may be stabilized at periodic orbits.

As for system (2), choose the generalized energy function as

. (8)

By calculation, we have the average value. Suppose y is adjustable, we adopt the following strategy to control system (2): when, no control is required; when and, if, then

,

and if, then

.

From simulation results we can see that the strategy is available to control system (2). Figure 9 and Figure 10 show the simulation results with different. From Figure 9 and Figure 10, we can see that with minimal energy method, Lü system can be stabilized at fixed point and periodic orbits.

4. Conclusions

We study the chaotic control of Lü system with several different methods. In the direct feedback scheme, Lü system is stabilized at equilibrium point and limit cycle successfully. In the adaptive time-delayed feedback scheme, feedback coefficient and delay time can be adjusted adaptively to stabilize Lü system at one of its original periodic orbits. In the minimal energy method, Lü system can be guided to fixed point and periodic orbits too. Numerical simulations show the effectiveness of our methods.

Direct feedback is the most common method for chaotic control. With linear or nonlinear, single-variable or multiple-variable feedback, it is available to the control of almost all chaotic systems, even multi-scroll systems [24] [25] and high-dimension systems. In the paper, we use this method to stabilize Lü system at its equilibrium or a limit cycle around its equilibrium. In the case, this method is based on Lyapunov stability theory, and the exact function of the system should be known before designing the control scheme. By the way, it’s hard to use the other two methods in the paper to stabilize a chaotic system at its original equilibrium because the equilibrium will be changed in the other two methods.

On the contrary, we don’t require the detailed information of chaotic systems in our adaptive time-delayed feedback method. Feedback coefficient and delay time can be adjusted adaptively during the control process. In order to realize the control of complex chaotic systems, such as multi-scroll systems [24] [25] or high-dimension systems, the feedback can also involve multiple variables, and the period of the controlled system will be a common multiple of the period of every variable. can be seemed as the fixed feedback form of our adaptive method, but numerical simulations are indispensable to verify a concrete adaptive control scheme effective or not.

As long as some variable(s) can be adjusted, the chaotic system may be controlled by minimal energy method. However, this method also depends on simulations. For a special chaotic system, proper can only be obtained by simulations. Even though, fortunately, by numerical simulations, we find that the available range of is very large.

Acknowledgements

The work was supported by Doctor Specific Funds of Dalian University.

References