International Journal of Modern Nonlinear Theory and Application
Vol.3 No.1(2014), Article ID:43804,9 pages DOI:10.4236/ijmnta.2014.31002
Reducibility of Periodic Quasi-Periodic Systems
Evi Ezekiel, Sangram Redkar
Department of Engineering, Arizona State University at Polytechnic Campus, Mesa, USA
Email: ssredkar@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 28 September 2013; revised 28 October 2013; accepted 5 November 2013
ABSTRACT
In this work, the reducibility of quasi-periodic systems with strong parametric excitation is studied. We first applied a special case of Lyapunov-Perron (L-P) transformation for time periodic system known as the Lyapunov-Floquet (L-F) transformation to generate a dynamically equivalent system. Then, we used the quasi-periodicnear-identity transformation to reduce this dynamically equivalent system to a constant coefficient system by solving homological equations via harmonic balance. In this process, we obtained the reducibility/resonance conditions that needed to be satisfied to convert a quasi-periodic system in to a constant one. Assuming the reducibility is possible, we obtain the L-P transformation that can transform original quasi-periodic system into a system with constant coefficients. Two examples are presented that show the application of this approach.
Keywords:L-P Transformation; Quasi-Periodic System; Reducibility

1. Introduction
A matrix function  with a square matrix of dimension
with a square matrix of dimension  is termed quasi-periodic with k incommensurable frequencies
is termed quasi-periodic with k incommensurable frequencies 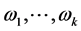 [1] [2] . A quasi-periodic function
[1] [2] . A quasi-periodic function 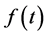 can be showed in the form
can be showed in the form
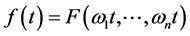 (1)
(1)
where a continuous function is 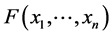 of period
of period ![]() in
in . In addition, we can always assume that
. In addition, we can always assume that 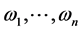 are independent [2] . As Moser [3] stated, the class of all almost periodic functions is not separable while
are independent [2] . As Moser [3] stated, the class of all almost periodic functions is not separable while  is. The integral of a quasi-periodic function is not quasi-periodic even if the mean value of
is. The integral of a quasi-periodic function is not quasi-periodic even if the mean value of 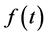 is zero [3] .
is zero [3] .
Let’s consider the linear equation
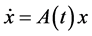 (2)
(2)
where 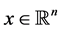 and
and 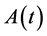 is a matrix depending quasi-periodically on time. The quasi-periodicity of
is a matrix depending quasi-periodically on time. The quasi-periodicity of 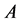 enables it possible to raise the Equation (2) to a system of linear equations [4] [5] on
enables it possible to raise the Equation (2) to a system of linear equations [4] [5] on 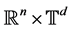 basically writing
basically writing
![]() (3)
(3)
where the Equation (2) is acquired when the initial value for ![]() is zero.
is zero.
Now let’s consider the matrix equation for (3), so that the lifted system [2] becomes
![]() (4)
(4)
Equation (2) is said to be reducible whenever there is a linear time-varying change of variables
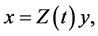 (5)
(5)
called Lyapunov-Perron (L-P) transformation [2] , which transforms the system into an equation like 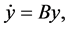 where
where 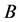 is a constant matrix. As Fink [6] mentioned, if
is a constant matrix. As Fink [6] mentioned, if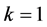 , then all systems are reducible by the Floquet theory. This view is also applicable for common linear systems [7] like
, then all systems are reducible by the Floquet theory. This view is also applicable for common linear systems [7] like
 (6)
(6)
and it means that, whenever a system like that is L-P reducible to a constant coefficients system like
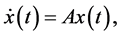 (7)
(7)
This will result in many properties of the original system “such as the growth of the solutions or their boundness” being the same as those of the reduced system with constant coefficients [2] .
The primary objective of this work is to develop a practical approach for reducibility of quasi-periodic system with strong parametric periodic excitation. It is noted that in the past, the researchers have studied quasi-periodic system where the order of quasi-periodicity is less than the order of the linear term [8] [9] as given by Equation (8)
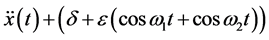 (8)
(8)
In this work, we relax this requirement. We assume the order of themost dominant “strong” periodic excitation to be of the same order as the constant term given by Equation (9) and use the L-F transformation and quasi-periodic near identity transformation to
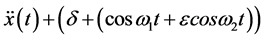 (9)
(9)
reduce the system to a constant form. This research will present a practical approach to achievereducibility of quasi-periodic system and will lay the groundwork for future efforts in optimizing such a process.
1.1. Floquet Theory Overview
Floquet theory is very useful for finding the response or stability of linear time-periodic equations [4] [10] [11] . Consider the linear periodic system
 (10)
(10)
 denotes the State Transition Matrix (STM) (fundamental solution matrix) that contains n linearly independent solutions of Equation (10) with the initial conditions
denotes the State Transition Matrix (STM) (fundamental solution matrix) that contains n linearly independent solutions of Equation (10) with the initial conditions  as
as 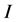 is an identity square matrix of dimension n.
is an identity square matrix of dimension n.
As such the following conditions hold:
1)  and, consequently 2)
and, consequently 2) 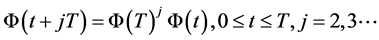
3) 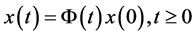
These conditions suggest that, if the solution is known for the first period, it can be designed for all time t. The matrix  is called the Floquet transition matrix (FTM). The next condition considers the stability of Equation (10). Let
is called the Floquet transition matrix (FTM). The next condition considers the stability of Equation (10). Let 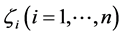 denote the eigenvalues of
denote the eigenvalues of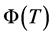 . System given by Equation (10) is asymptotically stable if all
. System given by Equation (10) is asymptotically stable if all  lie inside the unit circle of the complex plane. If one or more of the eigenvalues of the FTM has magnitude greater than one, the system is unstable. The Floquet multipliers are the eigenvalues
lie inside the unit circle of the complex plane. If one or more of the eigenvalues of the FTM has magnitude greater than one, the system is unstable. The Floquet multipliers are the eigenvalues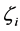 .
.
According to the Lyapunov-Floquet (L-F) theorem, STM (the fundamental matrix) 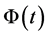 of equation (10) can be written as a product of two matrices as:
of equation (10) can be written as a product of two matrices as:
![]() (11)
(11)
where  is
is 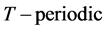 and
and 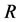 is a constant matrix, both, in general, are complex. There also exists factorization of the same form, where
is a constant matrix, both, in general, are complex. There also exists factorization of the same form, where 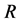 is a real constant matrix and
is a real constant matrix and 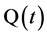 is real
is real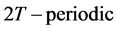 .
.  is called the
is called the 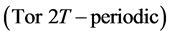 L-F transformation matrix [12] . For the details on computation of the L-F transformation and its applications, we refer the reader to references [13] -[15] .
L-F transformation matrix [12] . For the details on computation of the L-F transformation and its applications, we refer the reader to references [13] -[15] .
1.2. Quasi-Periodic System Reducibility
In the paper by Wooden and Sinha [15] , it is mentioned that an essential class of dynamical systems may be showed by a set of nonlinear differential equations with periodic/quasi-periodic coefficients multiplying the nonlinearity. They analyzed the system where the linear term was periodic but the nonlinear terms were quasi-periodic as given by equation
 (12)
(12)
where  is a matrix of constant coefficients,
is a matrix of constant coefficients, 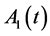 is matrix with time periodic coefficients and
is matrix with time periodic coefficients and  is a vector with quasi-periodic coefficients. The matrices have dimensions
is a vector with quasi-periodic coefficients. The matrices have dimensions  and the vector is
and the vector is 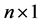 dimensional. The authors used the L-F transformation and nonlinear quasi-periodic transformations to study Equation (12) and obtained resonance conditions.
dimensional. The authors used the L-F transformation and nonlinear quasi-periodic transformations to study Equation (12) and obtained resonance conditions.
In the past, Arnold [10] demonstrated normal forms of quasi-periodic nonlinear systems with time-invariant linear part. Bogoljubov et al. [11] presented the reducibility of quasi-periodic systems to approximate time-invariant forms using a small parameter strategy. Even though small parameters/perturbation type techniques have been successfully used to study stability and reducibility of quasiperiodic systems [9] , these techniques are limited by small parameters multiplying the nonlinear and/or time-varying conditions. Belhaq et al. [16] considered a homogeneous Mathieu equation with quasi-periodic linear coefficients and a constant nonlinear coefficient. The small parameter strategy of multiple scales was used twice to the system to acquire an approximate time-invariant system. Researchers have used small parameter assumption to plot stability charts for quasiperiodic systems [17] [18] .
The system studied in this research is different that the systems studied earlier. Here, we consider the system of the form given by Equation (13)
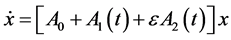 (13)
(13)
where 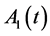 is the time periodic matrix
is the time periodic matrix  and
and 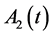 matrix has the coefficients with incommensurate frequencies and
matrix has the coefficients with incommensurate frequencies and  is a constant matrix of appropriate dimensions. We present technique to reduce Equation (13) to a constant coefficient system without any limitation on the magnitude of
is a constant matrix of appropriate dimensions. We present technique to reduce Equation (13) to a constant coefficient system without any limitation on the magnitude of  i.e. small parameter assumption. This paper is organized as follows. In section two, the reducibility formulation is presented and the resonance/reducibility conditions are derived. In section three, application of this approach is presented with two examples. Section four has discussion and conclusions.
i.e. small parameter assumption. This paper is organized as follows. In section two, the reducibility formulation is presented and the resonance/reducibility conditions are derived. In section three, application of this approach is presented with two examples. Section four has discussion and conclusions.
2. Reducibility Problem Formulation
Consider the time periodic part of Equation (13),
 (14)
(14)
The state transition matrix (STM) of Equation (11) can be factored as
![]() (15)
(15)
where 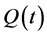 is typically
is typically , periodic such that
, periodic such that 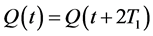 and
and 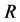 is a real-valued
is a real-valued ![]() constant matrix. Applying the L-F transformation
constant matrix. Applying the L-F transformation  to Equation (13) gives
to Equation (13) gives
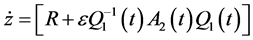 (16)
(16)
Application of modal transformation 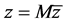 to Equation (16) converts the constant part of the system in the Jordan form, where
to Equation (16) converts the constant part of the system in the Jordan form, where 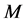 is eigenvector of R
is eigenvector of R
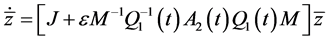 (17)
(17)
where ![]() is the Jordon Form of R and
is the Jordon Form of R and 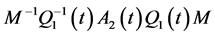 is quasi-periodic matrix with
is quasi-periodic matrix with . We use following near-identity transformation to Equation (17)
. We use following near-identity transformation to Equation (17)
 (18)
(18)
where the unknown nonlinear function 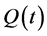 is quasi-periodic. Substituting Equation (18) in Equation (16), we obtain
is quasi-periodic. Substituting Equation (18) in Equation (16), we obtain
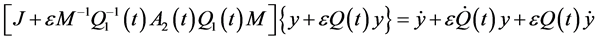 (19)
(19)
Assuming  and expanding Equation (19) and simplification, we obtain
and expanding Equation (19) and simplification, we obtain
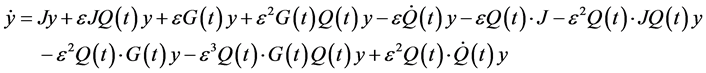 (20)
(20)
Now, if
 (21)
(21)
Then, Equation (20) reduces to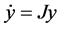 . Thus, quasi-periodic system given by Equation (16) will be reduced to a constant system.
. Thus, quasi-periodic system given by Equation (16) will be reduced to a constant system.
Equation (21) is similar to the homological equation obtained in the normal form reduction. By collecting the coefficient of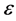 , we get the reducibility equation
, we get the reducibility equation
![]() (22)
(22)
For illustration, assume all the matrices in Equation (22) are ![]() of the form
of the form
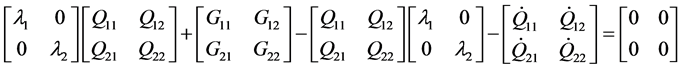 (23)
(23)
Equation (23) can be expanded in the scalar form as
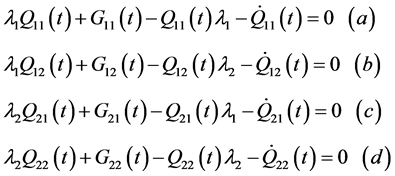 (24)
(24)
It can be noted that Equations (21a) and (21d) can be solved as
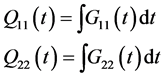 (25)
(25)
To find the solution of Equation (24b) and (24c), elements of 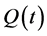 and
and 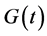 will have to be expanded in multiple Fourier series as
will have to be expanded in multiple Fourier series as
 (26)
(26)
where  are the unknown and
are the unknown and  known coefficients. Term by term comparison yields
known coefficients. Term by term comparison yields
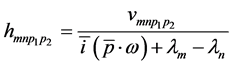 (27)
(27)
Thus, Equation (27) can be solved if
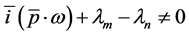 (28)
(28)
Equation (28) is called as the reducibility condition. Thus, a quasi-periodic system can be reduced to a constant system provided Equation (28) is satisfied. It is also noted that since the order of quasi-periodicity is , we obtain solution of
, we obtain solution of 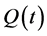 to the order
to the order . It is possible to extend this approach to higher orders of
. It is possible to extend this approach to higher orders of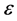 , if needed.
, if needed.
3. Applications
In this section, we present two examples—a commutative system and a quasi-periodic Mathieu equation. We apply the procedure discussed in Section two to reduce the quasi-periodic system to a constant one.
3.1. Commutative System
Consider the following commutative system
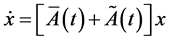 (29)
(29)
where
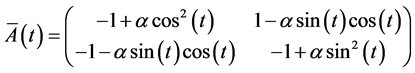
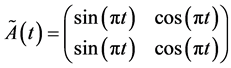 and
and 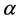 is a system parameter The L-F transformation for matrix
is a system parameter The L-F transformation for matrix 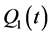 is
is
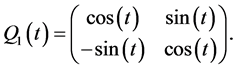 (30)
(30)
and
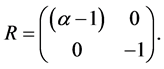
Applying the L-F Transformation  to Equation (31) yields
to Equation (31) yields
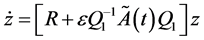 (31)
(31)
It is noted that for this special case matrix ![]() is in the Jordan form
is in the Jordan form![]() . Thus
. Thus
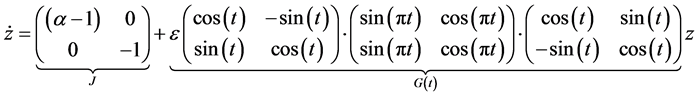 (32)
(32)
Equation (32) can be reduced to a constant coefficient system with the procedure discussed in section two. First a quasi-periodic near identity transformation 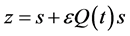 can be substituted in Equation (32) where
can be substituted in Equation (32) where 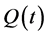 is the quasi-periodic matrix with unknown coefficients. The elements of this matrix have the form given by Equation (26) with
is the quasi-periodic matrix with unknown coefficients. The elements of this matrix have the form given by Equation (26) with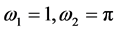 . At this point, collecting the terms of order
. At this point, collecting the terms of order 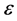 yields the homological equation
yields the homological equation
![]() (33)
(33)
Expanding  and
and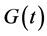 in the form given by Equation (26) and collecting the terms via harmonic balance yields the elements of
in the form given by Equation (26) and collecting the terms via harmonic balance yields the elements of 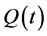 if the resonance condition given by Equation (28) is satisfied. Thus, we reduce the quasi-periodic system given by Equation (26) to a constant coefficient system given by Equation (31)
if the resonance condition given by Equation (28) is satisfied. Thus, we reduce the quasi-periodic system given by Equation (26) to a constant coefficient system given by Equation (31)
![]() (34)
(34)
To compare the results we integrate Equation (29) numerically and generate the time traces and phase plane. For the reduced system given by Equation (31), it is possible to find a closed form solution as
![]() (35)
(35)
where 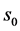 is the initial condition. Using the transformation
is the initial condition. Using the transformation 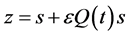 it is possible to obtain the closed form solution in
it is possible to obtain the closed form solution in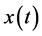 .
.
In Figure 1, the solutions of the original system and the reduced order system are compared. Time traces shown in red were obtained via numerical integration of Equation (29) and time traces in blue were obtained by solving the reduced constant coefficient system in the closed form (given by Equation (35))and mapping it back to original coordinates  via quasi-periodic near identity and L-F transformation. It can be observed that the time traces match quite well. In Figure 2, phase portraits of the original and reduced system are compared. It can be seen that the phase portraits also match quite well.
via quasi-periodic near identity and L-F transformation. It can be observed that the time traces match quite well. In Figure 2, phase portraits of the original and reduced system are compared. It can be seen that the phase portraits also match quite well.
3.2. Quasiperiodic Mathieu Equation
Consider a Quasiperiodic Mathieu equation given by
 (36)
(36)
where 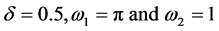 are incommensurate frequencies and
are incommensurate frequencies and ![]() is the small parameter. Equation (36) can be represented in the state space form as given by Equation (13) where
is the small parameter. Equation (36) can be represented in the state space form as given by Equation (13) where
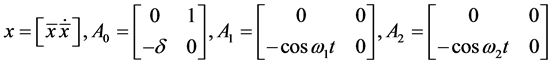 (37)
(37)
It is noted that the parametric excitation is strong and the L-F and modal transformation is applied to get Equation (38).
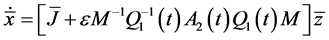 (38)
(38)

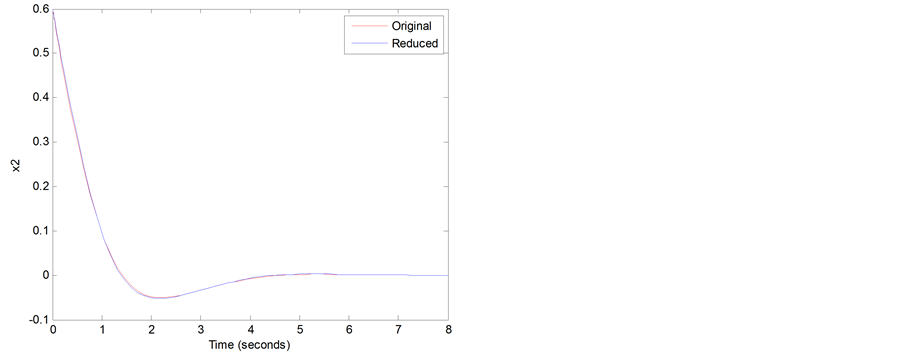
Figure 1. Time Trace Comparison.
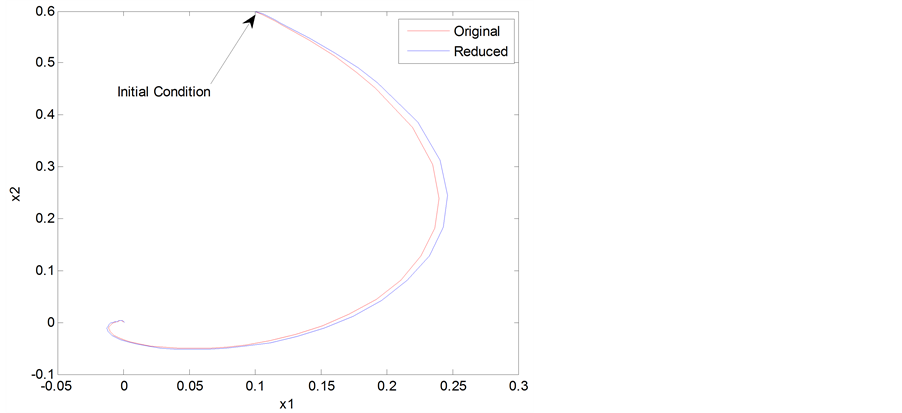
Figure 2. Phase portrait comparison.
where 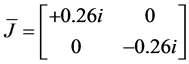 and the detailed expression for
and the detailed expression for  was obtained by Mathematica™. At this stage, as before, a quasi-periodic near identity transformation
was obtained by Mathematica™. At this stage, as before, a quasi-periodic near identity transformation 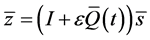 can be substituted. After collecting the terms of order ε Equation (35) can be obtained
can be substituted. After collecting the terms of order ε Equation (35) can be obtained
 (39)
(39)
Expanding 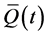 and
and  in the form given by Equation (23) and collecting the terms via harmonic balance, elements of
in the form given by Equation (23) and collecting the terms via harmonic balance, elements of 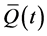 can be found out. It is noted that in this case the reducibility condition (given by Equation (25)) was satisfied. Thus, we could reduce the quasi-periodic system given by Equation (36) to a constant coefficient system given by Equation (40)
can be found out. It is noted that in this case the reducibility condition (given by Equation (25)) was satisfied. Thus, we could reduce the quasi-periodic system given by Equation (36) to a constant coefficient system given by Equation (40)
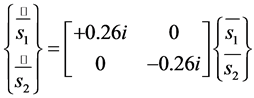 (40)
(40)
The solution of Equation (40) can be found in the closed form as
![]() (41)
(41)
where 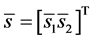 and
and ![]() is the vector of typical initial conditions. To compare the results we integrated Equation (36) numerically and generated the time traces and phase portrait. For the reduced system, we used Equation (41) andapplied the quasi-periodic transformation
is the vector of typical initial conditions. To compare the results we integrated Equation (36) numerically and generated the time traces and phase portrait. For the reduced system, we used Equation (41) andapplied the quasi-periodic transformation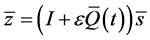 , L-F and modal transformation to obtain the time traces and phase portrait of vector
, L-F and modal transformation to obtain the time traces and phase portrait of vector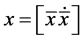 . Thesesolutions are compared in Figures 3 and 4. Figure 3 shows the time traces of the states and Figure 4 shows the phase portrait of the “Original” and “Reduced” states. It can be seen that these solutions match quite well.
. Thesesolutions are compared in Figures 3 and 4. Figure 3 shows the time traces of the states and Figure 4 shows the phase portrait of the “Original” and “Reduced” states. It can be seen that these solutions match quite well.
4. Conclusions
In this work, a new approach for reducibility of quasi-periodic system analysis is presented using the L-F transformation and quasi-periodic near identity transformation. In this process, one obtains the reducibility conditions and the quasi-periodic system can be converted to a constant coefficient system provided the reducibility conditions are satisfied.
The resulting homological is expanded using multiple Fourier series which can solved for the unknown Fourier coefficients of the near-identity transformation coefficients via harmonic balance. Two examples presented a commutative system and quasi-periodic Mathieu equation. In both cases, the parametric excitation is
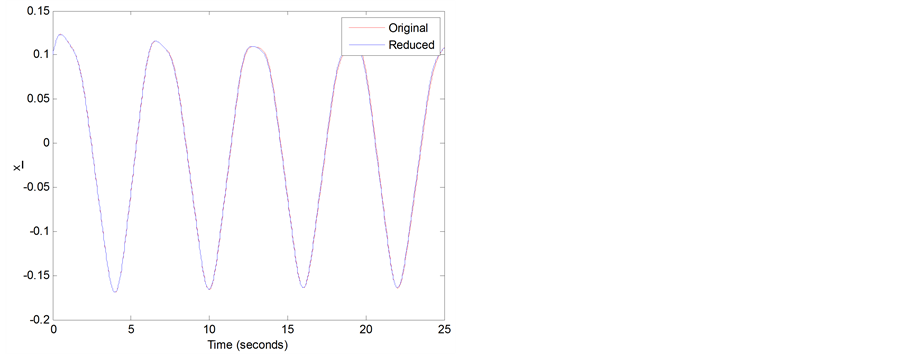
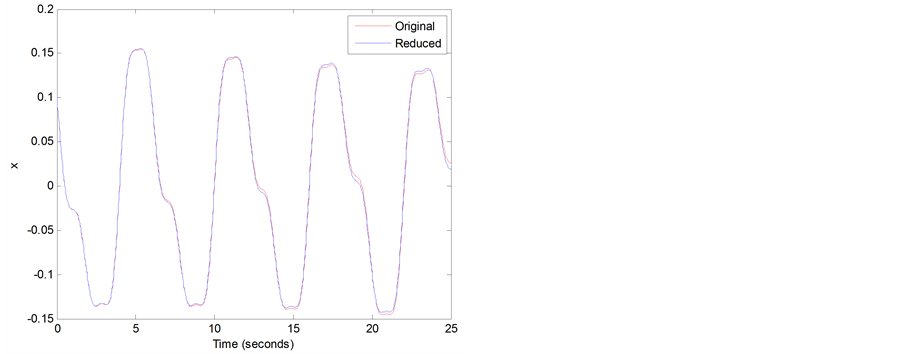
Figure 3. Time Trace Comparison.

Figure 4. Phase Plane Comparison.
strong. Simulations and phase plane were plotted to compare results from numerical integration and closed form solution. It can be seen that the results matched quite well. Thus, if the reducibility conditions are satisfied then the quasi-periodic systems with strong parametric excitation can be reduced to a constant form using the L-F transformation. It is possible to analyze or control this reduced order time invariant system and map the results back using appropriate transformations to study and control original quasi-periodic system.
References
- Murdock, J.A. (1978) On the Floquet Problem for Quasiperiodic Systems. Proceedings of the American Mathematical Society, 68, 179. http://dx.doi.org/10.1090/S0002-9939-1978-0481275-8
- Jorba, A. and Simó, C. (1992) On the Reducibility of Linear Differential Equations with Quasi-Periodic Coefficients. Journal of Differential Equations, 98, 111-124 http://dx.doi.org/10.1016/0022-0396(92)90107-X
- Moser, J. (1966) On the Theory of Quasi-Periodic Motions. Siam Review, 8, 145-172. http://dx.doi.org/10.1137/1008035
- Puig, J. (2002) Reducibility of Linear Equations with Quasi-Periodic Coefficients. A Survey. www.maia.ub.edu/dsg/2002/0201puig.pdf
- Chavaudret, C. (2010) Reducibility of Quasi-Periodic Cocycles in Linear Lie Groups. Ergodic Theory and Dynamical Systems, 31, 741-769 http://dx.doi.org/10.1017/S0143385710000076
- Fink, A.M. (1974) Almost Periodic Differential Equations, Lecture Notes in Math. Springer Verlag, Berlin and New York, 377.
- Richard, R., Randolph, Z. and Rachel, H. (1997) A Quasi-Periodic Mathieu Equation. Series on Stability, Vibration and Control of Systems Series B, 2, 203-221. http://dx.doi.org/10.1142/9789812831132_0009
- Zounes, R. and Rand, R. (1998) Transition Curves for the Quasi-Periodic Mathieu Equation. SIAM Journal on Applied Mathematics, 58, 1094-1115. http://dx.doi.org/10.1137/S0036139996303877
- Xu, J. and Jiang, S. (2011) Reducibility for a Class of Nonlinear Quasi-Periodic Differential Equations with Degenerate Equilibrium Point under Small Perturbation. Ergodic Theory and Dynamical Systems, 31, 599-611. http://dx.doi.org/10.1017/S0143385709001114
- Arnold, V.I. (1988) Geometrical Methods in the Theory of Ordinary Differential Equations. Springer-Verlag, New York.
- Bogoljubov, N.M., Mitropoliskii, J.A. and Samoilenko, A.M. (1976) Methods of Accelerated Convergence in Nonlinear Mechanics. Springer-Verlag, New York.
- Sinha, S.C. and Butcher, E.A. (1997) Symbolic Computation of Fundamental Solution Matrices for Linear Time Periodic Dynamical Systems. Journal of Sound and Vibration, 206, 61-85.
- Sinha, S.C. and Gourdon, E. (2005) Control of Time-Periodic Systems via Symbolic Computation with Application to Chaos Control. Communications in Nonlinear Science and Numerical Simulation, 10, 835-854.
- Sinha, S.C. and Joseph P. (1994) Control of General Dynamic Systems with Periodically Varying Parameters via Liapunov-Floquet Transformation. Journal of Dynamic Systems, Measurement, and Control, 116, 650-658. http://dx.doi.org/10.1115/1.2899264
- Wooden, S.M. and Sinha, S.C. (2007) Analysis of Periodic-Quasiperiodic Nonlinear Systems via Lyapunov-Floquet Transformation and Normal Forms. Journal of Nonlinear dynamics, 47, 263-273.
- Belhaq, M., Guennoun, K. and Houssni, M. (2002) Asymptotic Solutions for a Damped Non-Linear Quasi-Periodic Mathieu Equation. International Journal of Non-Linear Mechanics, 37, 445-460. http://dx.doi.org/10.1016/S0020-7462(01)00020-8
- Puig, J. and Simó, C. (2011) Resonance Tongues in the Quasi-Periodic Hill-Schrödinger Equation with Three Frequencies. Regular and Chaotic Dynamics, 16, 62-79. http://dx.doi.org/10.1134/S1560354710520047
- Broer, H.W. and Simó, C. (1998) Hill’s Equation with Quasi-Periodic Forcing: Resonance Tongues, Instability Pockets and Global Phenomena. Boletim da Sociedade Brasileira de Matemática, 29, 253-293. http://dx.doi.org/10.1007/BF01237651

