International Journal of Modern Nonlinear Theory and Application
Vol.2 No.1(2013), Article ID:28678,7 pages DOI:10.4236/ijmnta.2013.21002
Classic and Non-Classic Soliton Like Structures for Traveling Nerve Pulses
1Facultad de Ciencias, Universidad Autónoma del Estado de México, Toluca de Lerdo, México
2Plantel Nezahualcoyotl, Universidad Autónoma del Estado de México, Toluca de Lerdo, México
Email: maaguerog@uaemex.mx
Received December 10, 2012; revised January 18, 2013; accepted January 28, 2013
Keywords: Compactons; Nonlinear Waves; Solitons; Nerve Pulse; Molecular Waves
ABSTRACT
After some reduction procedure made on the nonlinear evolution equation for nerve pulses, based on thermodynamic principles, new classic and non-classic traveling solutions have been obtained. We have studied this model for particular values in the parameter space, and obtained both the bell and compacton like solutions. These nonlinear traveling waves could be responsible for transmitting efficiently the necessary information along the axons. The non-classic structures named as compactons, due to their robust configuration, could be considered in some sense a more realistic type of nonlinear chargers of information. The last solutions do not have tails and as adiabatic waves could propagate along the nerve with constant velocity that could be equal, smaller or higher than the sound velocity.
1. Introduction
One of key fundamental problems in biophysics is to understand how nature makes to carry information without significant distortion along distances between two considerable long separated centers. Now it is well established that the dynamic of ionic currents through voltage channels is responsible for the change of the membrane potential in nerve tissues. As is well known the first measurements on ionic currents were performed by Hodgkin and Huxley (HH) in the 50s [1]. In 1966 Katz [2] proposed for traveling pulse the soliton traveling pulse as a simplest model for this activity.
Later, the Hodgkin and Huxley system was developed independently by Richard FitzHugh, and Jin-ichi Nagumo [3,4]. Based on the work of Balthazar Van Der Pol, FitzHugh proposed a simplified neuronal model of Hodgkin and Huxley. For its part, Nagumo suggested as analogous neuronal, a nonlinear electrical circuit, controlled by an equation system also similar to those of Van Der Pol currents. The proposed simplified analog of these authors, is called FitzHugh-Nagumo model. Being susceptible fairly complete analysis, the FHN system allows a qualitative understanding of the phenomenon of excitability, from the point of view of dynamic systems [5] and constitutes a classical model of neurophysiology. The current importance of this model is beyond the scope of biophysics and neurophysiology, being of interest to researchers who need to understand the wide range of nonlinear phenomena accompanying the phenomenon of excitability. By introducing an approximate scheme to the famous model of Hodgkin-Huxley, Muratov in his paper [6] obtained solitary wave pulse for nerve conductance and obtained the value of velocities that are in agreement with experimental results.
Recently, Heimburg and coworkers have developed a model for nerve pulses that support soliton like solutions [7-10]. The model is constructed considering the nerve axon as a one dimensional cylinder with lateral density excitations moving along the axes that is represented by the coordinate z. This model shows the appearance of lipid phase transition slightly below physiological temperatures. Given measured values of the compression modulus as a function of lateral density and frequency, soliton properties can be determined by the velocity of the traveling waves. That is, resuming we can say that this theory is based on the lipid transition from a fluid to a gel phase at slightly below of body temperatures. The effects of nonlinearity and dispersion as is common would be responsible for appearance of soliton like structures in nerve membrane in the gel state [10] and more recent results on soliton and periodical solutions can be found in [11].
On the other hand, as is well known, classical solitons possess infinite tails that could implicate some distortions at long distances far from the excited zone. This constriction could also be applied to nerve solitons as well. However, according to several important results from experiments made on nerve axon, there is a suggestion that the nerve pulse need to be narrow and probably they could posses depreciable tails. Fortunately, several types of non-classic solutions without or depreciable tails were found in a wide class of nonlinear processes in physics.
We suppose that along the axon, not only well famous bell solitons could propagate, but also non-classical soliton like solutions named compactons could be excited and travel carrying needed information. Thus, our main interest in this contribution is to show the appearance of compactons along the nerve, that is, solitons without tails. This nonlinear robust entity will eventually fit more realistically to the features of that waves that are reported on nerve pulses in the literature. We use the model of Heimburg and coworkers [9] and by applying the trivial boundary condition we found some non-classic soliton like solutions. Thus, in the next section we briefly expose the main nonlinear evolution equation for nerve pulses. In the III section we show that compact solutions with the trivial boundary condition could appear and will travel with sonic, subsonic and supersonic velocities along the nerve. The section IV is devoted to discuss the main properties of the found solutions, and finally in the last section we discuss some features around the found solutions and outline further implications of the model presented.
2. Equation of Motion for Nerve Pulses
The detailed discussion on methods and proposals for obtaining the nonlinear differential equation which is the subject of our analysis, could be found in the appropriated literature, see for example [7-10]. The theory is based on hydrodynamic properties of a density pulse in the presence of dispersion. The authors started with the classic wave propagation equation in the absence of dispersion along the quasi-one dimensional axon:
 (1)
(1)
being 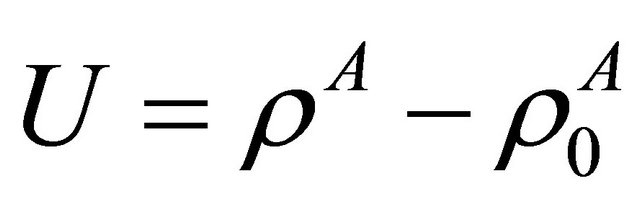 the change of density in the membrane,
the change of density in the membrane, 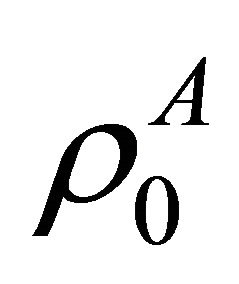 is the density of the membrane at physiological condition slightly above of melting transition. This “field” is supposed to have dependence of coordinate x and time t. The excitations are moving along the coordinate x. Here c is the sound velocity with the value
is the density of the membrane at physiological condition slightly above of melting transition. This “field” is supposed to have dependence of coordinate x and time t. The excitations are moving along the coordinate x. Here c is the sound velocity with the value
 , being
, being 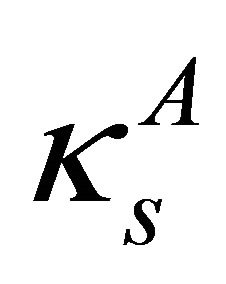 the compressibility. Subsequently, it is added the additional term responsible for dispersive effects
the compressibility. Subsequently, it is added the additional term responsible for dispersive effects . This term appears by experimental evidence on the relation between frequencies and velocities. For getting available nonlinear real dispersion relation the next term after the second derivative with respect to the variable x would stay the corresponding fourth derivative [11]. Next, Since the compressibility depends on the “field” U in the similar fashion of the Kerr Effect from nonlinear optics (is this the Nerve Kerr effect in biomembranes?) it is assumed that the velocity of the traveling waves can be represented in terms of Taylor series around the velocity of sound and now depends on the variable U as [9]
. This term appears by experimental evidence on the relation between frequencies and velocities. For getting available nonlinear real dispersion relation the next term after the second derivative with respect to the variable x would stay the corresponding fourth derivative [11]. Next, Since the compressibility depends on the “field” U in the similar fashion of the Kerr Effect from nonlinear optics (is this the Nerve Kerr effect in biomembranes?) it is assumed that the velocity of the traveling waves can be represented in terms of Taylor series around the velocity of sound and now depends on the variable U as [9]
 . (2)
. (2)
Finally, one can conclude that the partial differential equation for propagating waves can be represented as
 . (3)
. (3)
As can be easily seen this equation is similar if we restrict ourselves to take only the first two terms of the Taylor series in the rhs of Equation (2), to the well known Boussinesq like equation.
 (4)
(4)
It is possible then to study the nerve pulse in the framework of a completely integrable system like Boussinesq one (with restrictions) as a very special case for which the solutions obtained there could fit some experimental results. The Boussinesq like Equation (4) describes in addition to the bright or regular solutions, also singular or anti-cusp travelling solitons [12]. For these solitons (for instances, superficial waves under gravity, ionic acoustic waves) with wave numbers  their vacuum state will not collapse under the effect of weak perturbations like
their vacuum state will not collapse under the effect of weak perturbations like 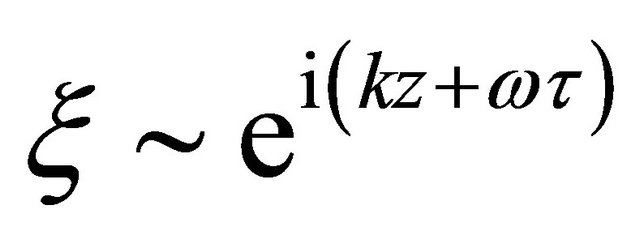 [13]. The complete analysis at the first approximation leading to the well posed or improved Boussinesq equation should be reported elsewhere.
[13]. The complete analysis at the first approximation leading to the well posed or improved Boussinesq equation should be reported elsewhere.
Despite the great effort for research concerning these type of models, and results, there is a question that still is waiting its successful solution. Indeed these theories predict the appearance of solitary waves with broad extension i.e. broad excitation region that contradicts experiment results. The experiments made with nerve pulses show the existence of narrow localized region of excitation. Thus, there is a big possibility that these pulses are in fact solitons but without tails. As is well known the classical solitons possess tails that could eventually interact at long distances that subsequently would degenerate the whole pulse to charge the needed information. So, the effort in this sense will be assumed to find solitons without tails i.e. solitary waves named regular or singular compactons.
As is well known, such solution with finite span is currently found in many natural processes. Thus, in this direction Rosenau and Hyman [14] discovered the compactons in the generalized nonlinear model of KdV equations that described the pattern formation in liquid drops. The equation they analyzed was the modified KdV (m, n) equation
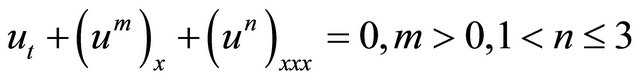 . (5)
. (5)
For the case m = 2, n = 2 It is possible to found
 (6)
(6)
where the solution is valid only inside the interval , and vanishes outside of this interval. These solutions including interact elastically like hard spheres do not possess infinite tails. The invariance under the transformation
, and vanishes outside of this interval. These solutions including interact elastically like hard spheres do not possess infinite tails. The invariance under the transformation  and
and 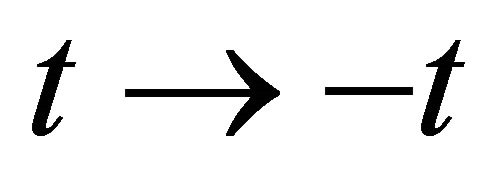 produces the anticompactons.
produces the anticompactons.
After this important discovery, compactons have found diverse applications in natural science, we cite here a few of them, for example in viscous films [15], DNA dynamics [16], ocean dynamics [17], nonlinear lattices [18], stability of compactons was investigated in [19], etc.
3. Traveling Non Classic Solutions
Let us investigate different kind of solutions that can be obtained by making suitable transformations of parameter values on the Equation (3). By making the standard transformation for considering the existence of traveling waves along the nerve, we introduce the new independent variable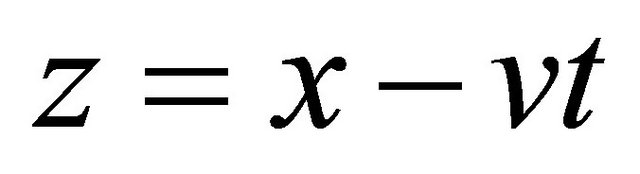 . Thus, the Equation (3) can be transformed to the next one
. Thus, the Equation (3) can be transformed to the next one
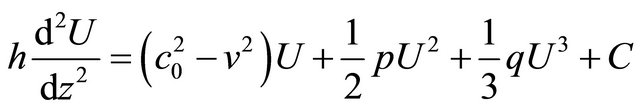 (7)
(7)
here C is a constant that is obtained after integration. This equation is very similar to a common equation that represents the Newton second law of mechanics. After subsequent standard transformation one can obtain the next equation
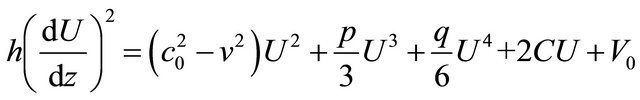 (8)
(8)
with being 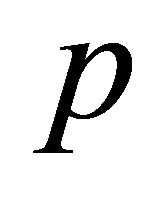 and
and  the parameters that appear in the Taylor expansion and
the parameters that appear in the Taylor expansion and  the constant of integration.
the constant of integration.
Now let us study this equation by taking in mind the trivial boundary condition, that means at long distances from the main excited zone the perturbation pulse vanishes and also its first derivative. Thus, we have for this boundary condition the standard requirement
 . (9)
. (9)
By applying this restriction the constant of integration 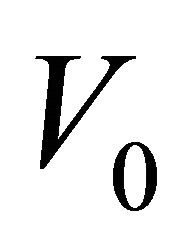 satisfies:
satisfies: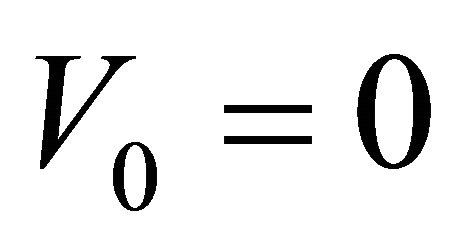 . It is important to mention that this value does not depend on any experiment conditions, the only restriction is that far from the excited zone of excitation the perturbation wave disappears.
. It is important to mention that this value does not depend on any experiment conditions, the only restriction is that far from the excited zone of excitation the perturbation wave disappears.
3.1. Traveling Solutions with Sound Velocity
First, let us consider the case: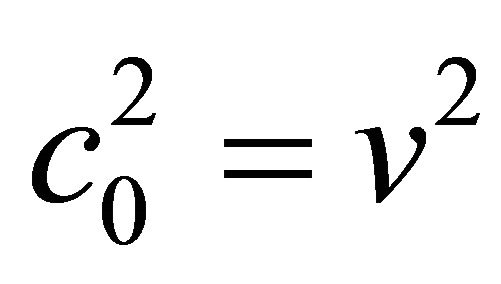 , when the nonlinear wave will move with the sound velocity along the axis z. Analyzing the possible consequences of this reduction, one can find that at the maximum amplitude value of solitary waves the right hand side of the Equation (8) for trivial boundary condition has three solutions, i.e. we face with an algebraic cubic equation. At the simplest case when
, when the nonlinear wave will move with the sound velocity along the axis z. Analyzing the possible consequences of this reduction, one can find that at the maximum amplitude value of solitary waves the right hand side of the Equation (8) for trivial boundary condition has three solutions, i.e. we face with an algebraic cubic equation. At the simplest case when 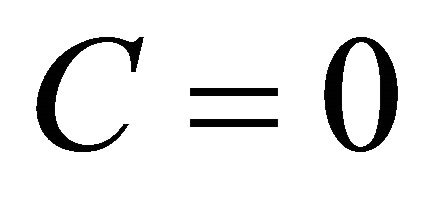 we can obtain two solutions for the U difference density. So, in both cases the maximum amplitude (when
we can obtain two solutions for the U difference density. So, in both cases the maximum amplitude (when  and
and ) of possible solitons is not equal to zero and the solution could exist as we demonstrate in the next subsection. Thus, we perform analytic studies for two sub cases, indeed.
) of possible solitons is not equal to zero and the solution could exist as we demonstrate in the next subsection. Thus, we perform analytic studies for two sub cases, indeed.
1) Sub-case: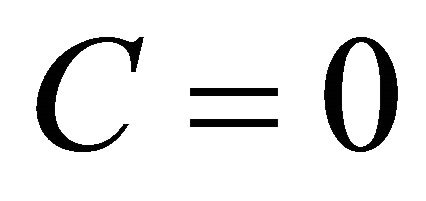 . In this simple case by integrating the Equation (8) we obtain the following solution
. In this simple case by integrating the Equation (8) we obtain the following solution
 . (10)
. (10)
By avoiding singular behaviors, the possible solution in this case is achieved by assuming the negative value of the parameter q. If this is satisfied, we can obtain a solitary wave that resemble the well known bell like soliton, see Figure 1. This analytic solution is named also algebraic soliton solution. Such solutions are less tightly localized than their hyperbolic counterparts; their tails fall

Figure 1. Algebraic soliton that travels with same velocity of sound along the axon. For illustrative purposes we put the following values for parameters: p = 3, q = −18. The high amplitude corresponds to small values of parameter p.
off with a power-law distribution, i.e., algebraically.
2) Sub-case: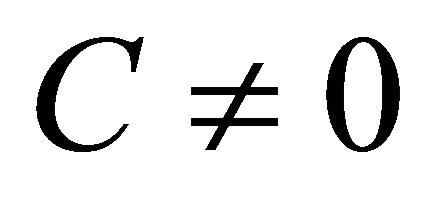 . For this sub-case it was also possible to find a particular physical interesting compact solution when the parameters of the equation of motion (8) satisfy the condition
. For this sub-case it was also possible to find a particular physical interesting compact solution when the parameters of the equation of motion (8) satisfy the condition
 . (11)
. (11)
For all compact type solutions we will follow the next strategy. Compacton solutions will be constructed by patching a compact portion of a periodic solution that is zero at both ends to a solution that vanishes outside the compact region to give a weak solution to the equation. We see that the condition for a weak solution for Equation (3) in the case of traveling waves with independent variable  is that the jump across the boundary of the equation of motion at
is that the jump across the boundary of the equation of motion at 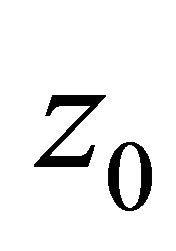 is
is
 . (12)
. (12)
The integration of the Equation (8) yields the following compact soliton like solution
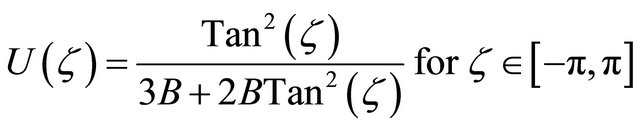 (13)
(13)
with the new variable 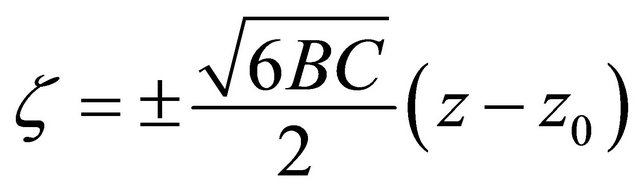 and the parameter
and the parameter .
.
This solution survive only in the segment mentioned above and exactly vanishes outside of this region and satisfies the trivial boundary condition. The points  are that points where the solutions and its first derivative vanish and satisfy the condition of solvability (12). Nextit is assumed that
are that points where the solutions and its first derivative vanish and satisfy the condition of solvability (12). Nextit is assumed that 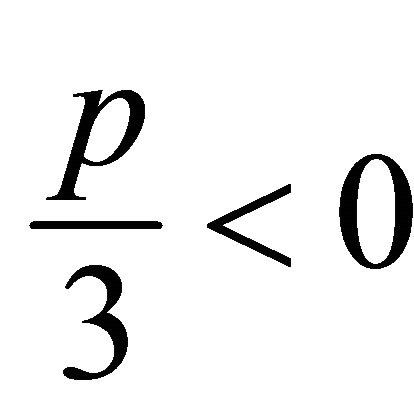 or
or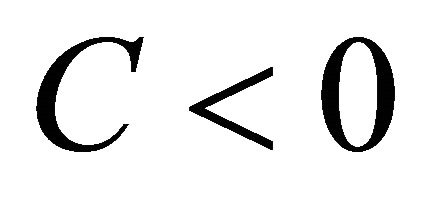 . The Figure 2 shows that this solution does not possess the long tails and is confined in a narrow segment of the nerve membrane.
. The Figure 2 shows that this solution does not possess the long tails and is confined in a narrow segment of the nerve membrane.
3.2. Traveling Compact Soliton Solutions When 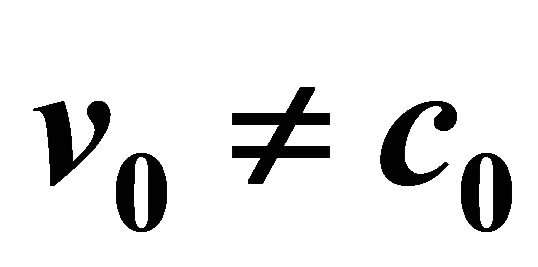
Now we can show other type of solutions that support the thermodynamic model [1]. We will investigate the solutions that have different velocities which has the sound. Again we use the Equation (8) but now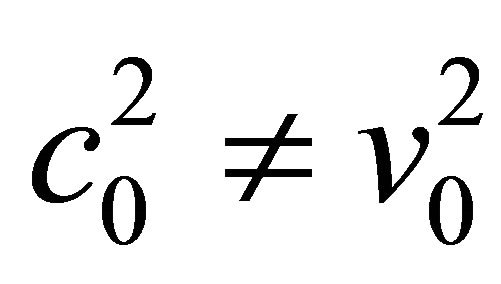 . If this is the case, we obtain solutions that resemble the well known compact like solitons. For this case, we slightly transform the right hand side of the Equation (8)
. If this is the case, we obtain solutions that resemble the well known compact like solitons. For this case, we slightly transform the right hand side of the Equation (8)
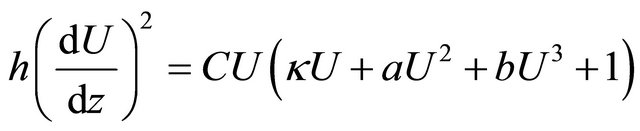 (14)
(14)

Figure 2. Compact soliton like structures that travels with the same velocity of sound along the axon. Here the parameters we used are ζ0 = 1.57, B = 0.33, C = 4.
with the renamed parameters
 . (15)
. (15)
Without lost of generality we can choice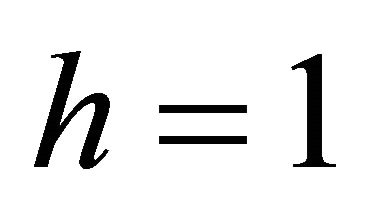 . In order to solve the differential Equation (14) it seems natural to introduce the following ansatz: Soliton like structures are available if the parameters of the strong model satisfy the following relation:
. In order to solve the differential Equation (14) it seems natural to introduce the following ansatz: Soliton like structures are available if the parameters of the strong model satisfy the following relation:
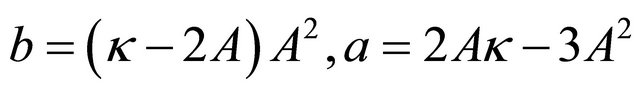 . (16)
. (16)
Then, after integration we again obtain a perfect compact like solution.
When this is satisfied, one trivially can obtain the solution for the density displacements 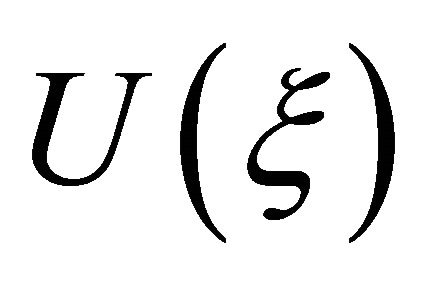 that takes the form of compact soliton like solution
that takes the form of compact soliton like solution
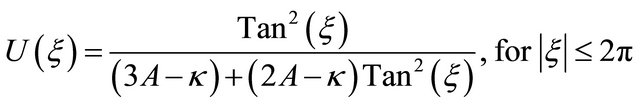 (17)
(17)
with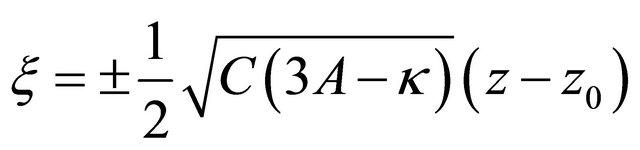 . As can be observed this specific solution exists by avoiding singularities i.e. in the particular case only for negative parameter values
. As can be observed this specific solution exists by avoiding singularities i.e. in the particular case only for negative parameter values
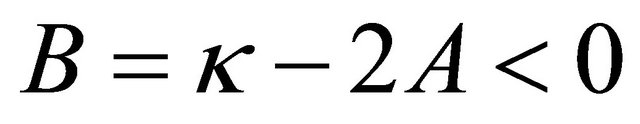 . (18)
. (18)
The Figure 3 shows the robust configuration of the soliton like solution. For these moving compactons with velocities differing from the sound one, the parameters a and b satisfy the following relation
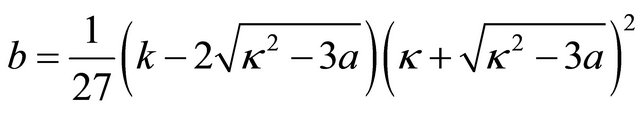 . (19)
. (19)
This expression depends on the soliton velocity by virtue of Equation (15). Outside of this dependence between the parameters the solutions probably will not admit compact support. The Figure 4 is the graphic representation
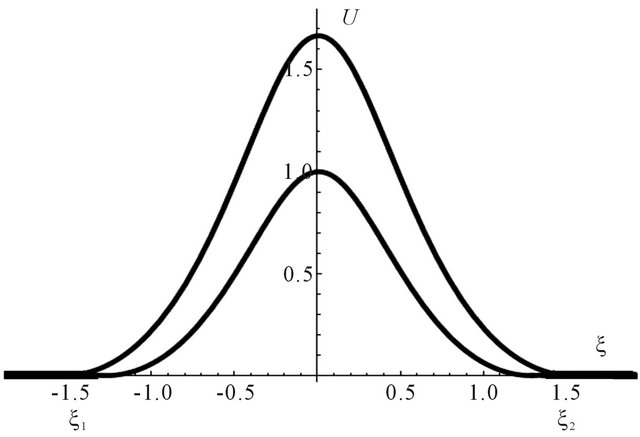
Figure 3. Subsonic traveling compacton like structure, similar to the case of sonic compactons. Here the utilized parameters are ξ0 = 1.57, A = 1, k = 1, C = 2.

Figure 4. The Taylor coefficients p, q from Equation (8) are related as shown in this picture according to the Equation (19) in order to find traveling compact solutions.
of the Equation (19). This expression gives to us the wide spectrum for using the parameter values.
By deploying the constraint (18) we obtain the parameter region of available velocities. Thus, when 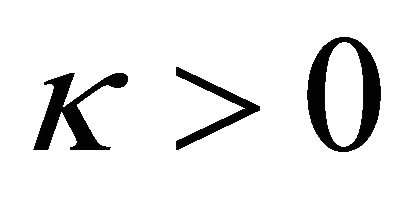 the velocity corresponds to subsonic waves, i.e.
the velocity corresponds to subsonic waves, i.e.
 . (20)
. (20)
If the values of 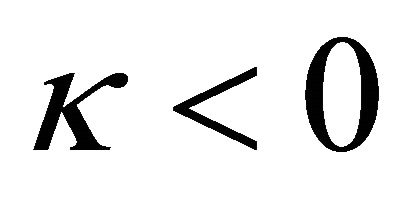 we obtain supersonic soliton waves with the next segment of values
we obtain supersonic soliton waves with the next segment of values
 . (21)
. (21)
One of the implications of these relations is that it would travel along the axon robust solitonic waves with speed greater than the sound velocity.
4. Energy of the Classical and Non-Classical Structures
The energy of solutions obtained for the ordinary nonlinear differential equation i.e. for traveling solutions can be calculated by using the energy density, which in some sense could be considered as energy density of a mechanical analog particle. The integration with respect to the variable  in the interval
in the interval  for compactons can be directly evaluated using the energy density. From the Equation (8) one can notice that the kinetic energy is equal to the potential one for the “mechanical analog particle”. This leads to find the total energy as
for compactons can be directly evaluated using the energy density. From the Equation (8) one can notice that the kinetic energy is equal to the potential one for the “mechanical analog particle”. This leads to find the total energy as
 (22)
(22)
with the “potential” piece of energy density
 . (23)
. (23)
Thus for the first algebraic soliton that moves with the same sound velocity the energy in dependence of the main parameters p and q is expressed as (where h = 1)
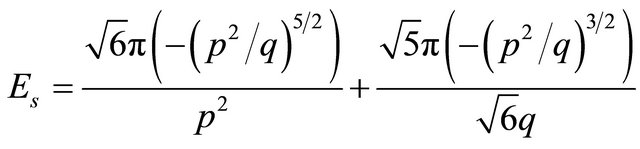 (24)
(24)
The energy for the second compacton solution that moves with the sound velocity is
 (25)
(25)
with .
.
Finally the last compacton solution has the following expression for its energy.
 .
.
This total energy depends on the velocity of the nonclassical solution. For avoiding singular solutions, when the values , traveling compact solution could emerge only when the velocities satisfy the relation
, traveling compact solution could emerge only when the velocities satisfy the relation , that is in complete accordance with the previous analysis made on the parameter space (18) for obtaining subsonic and also supersonic compact solutions. Here the parameters A and
, that is in complete accordance with the previous analysis made on the parameter space (18) for obtaining subsonic and also supersonic compact solutions. Here the parameters A and  are determined by the Equations (15) and (16).
are determined by the Equations (15) and (16).
5. Conclusion
We have discussed in this contribution the appearance of classical and non-classical soliton like pulses along the axon based on the pioneering work of [9]. The classical bell shape soliton shows infinite tails in contrast to the non classical solitons i.e. compactons without tails. These solutions could eventually be responsible for various fundamental processes inside the nerve. The evaluation of density displacements U along the nerve can be carried out straightaway by integrating their corresponding nonlinear equations. We consider that the displacements vanish at distances sufficiently far from the excitated zone. Therefore, in both direction of the axis , at long distances from the active zone, the density displacements will disappear forming the physical interesting case of zero boundary conditions. By taking in mind this physical reason and by integrating the nonlinear equation proposed in the work (3), for specific parameter regions, several soliton like solutions have been obtained. We have found solutions that move with the same velocity of the sound i.e. sonic solitons and also subsonic and supersonic compactons. These last structures could represent apparently more realistic the propagation of nerve pulses with narrow width along the quasi-one-dimensional model of axons. The compact solutions do not possess the infinite tails like common traditional solitons and are similar to hard spheres. They appear as a consequence of the physical trivial boundary condition and weak condition of solvability plus due to some restrictions on the parameter space of the model. The velocity of the traveling compactons is restricted by the values of physical concrete parameter values, i.e. by the relation (18) where k is defined from Equation (15). This inequality determines the maximum value of the pulse velocity. This means that these waves could charge the information efficiently faster between the two significant separated centers along the nerve axon. It should be interesting to check which one or both of these possibilities take place in real experiments. The properties (including its shape and its energy) can be determined uniquely as a function of compacton velocity. Given a measured compacton velocity, the theory contains freely adjustable parameters and has the virtue of being feasible. As soon as the nonlinear excitations in whichever segment of the axon structure is being activated by the presence of external agents for example, phonons, etc, nonlinear compacton waves could appear, describing realistically the density displacements.
, at long distances from the active zone, the density displacements will disappear forming the physical interesting case of zero boundary conditions. By taking in mind this physical reason and by integrating the nonlinear equation proposed in the work (3), for specific parameter regions, several soliton like solutions have been obtained. We have found solutions that move with the same velocity of the sound i.e. sonic solitons and also subsonic and supersonic compactons. These last structures could represent apparently more realistic the propagation of nerve pulses with narrow width along the quasi-one-dimensional model of axons. The compact solutions do not possess the infinite tails like common traditional solitons and are similar to hard spheres. They appear as a consequence of the physical trivial boundary condition and weak condition of solvability plus due to some restrictions on the parameter space of the model. The velocity of the traveling compactons is restricted by the values of physical concrete parameter values, i.e. by the relation (18) where k is defined from Equation (15). This inequality determines the maximum value of the pulse velocity. This means that these waves could charge the information efficiently faster between the two significant separated centers along the nerve axon. It should be interesting to check which one or both of these possibilities take place in real experiments. The properties (including its shape and its energy) can be determined uniquely as a function of compacton velocity. Given a measured compacton velocity, the theory contains freely adjustable parameters and has the virtue of being feasible. As soon as the nonlinear excitations in whichever segment of the axon structure is being activated by the presence of external agents for example, phonons, etc, nonlinear compacton waves could appear, describing realistically the density displacements.
6. Acknowledgements
Authors are indebted to Professor V. G. Makhankov for constant support and discussions. We acknowledge the efforts of SIEA-UAEMEX for supporting the fundamental research and also the financial aid of Secretaría de Educación Pública de México (SEP) under the project FEO1/2012 103.5/12/2126 for developing research scientific groups.
REFERENCES
- A. L. Hodgkin and A. F. Huxley, “A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve,” The Journal of Physiology, Vol. 117, No. 4, 1952, pp. 500-544.
- B. Katz, “Nerve, Muscle, and Synapse,” Mc Graw-Hill, New York, 1966.
- R. Fitzhugh, “Impulses and Physiological States in Theoretical Models,” Biophysical Journal, Vol. 1, No. 6, 1961, pp. 445-466. doi:10.1016/S0006-3495(61)86902-6
- J. Nagumo, S. Arimoto and S. Yoshizawa, “An Active Pulse Transmission Line Simulating Nerve Axon,” Proceedings of the IRE, Vol. 50, No. 10, 1962, pp. 2061- 2070.
- F. Ongay and M. Agüero, “Bifurcaciones del Sistema Fitzhugh Nagumo,” Ciencia Ergo Sum, Vol. 17, No. 3, 2011, pp. 295-306.
- C. B. Muratov, “A Quantitative Approximation Scheme for the Traveling Wave Solutions in the Hodgkin-Huxley Model,” Biophysical Journal, Vol. 79, No. 6, 2000, pp. 2893-2901. doi:10.1016/S0006-3495(00)76526-X
- T. Heinburg and A. Jackson, “On Soliton Propagation in Biomembranes and Nerves,” PNAS, Vol. 102, No. 28, 2005, pp. 9790-9795. doi:10.1073/pnas.0503823102
- B. Lautrup, R. Appali, A. D. Jackson and T. Heimburg, “The Stability of Solitons in Biomembranes and Nerves,” European Physical Journal E, Vol. 34, No. 6, 2011, pp. 1-9. doi:10.1140/epje/i2011-11057-0
- R. Appali, U. Van Rienenand and T. Heimburg, “A Comparison of the Hodgkin-Huxley Model and the Soliton Theory for the Action Potential in Nerves,” Advances in Planar Lipid Bilayers and Liposomas, Vol. 16, 2012, pp. 271-279. doi:10.1016/B978-0-12-396534-9.00009-X
- E. V. Vargas, et al., “Periodic Solutions and Refractory Periods in the Soliton Theory for Nerves and the Locust Femoral Nerve,” Biophysical Chemistry, Vol. 153 No. 2-3, 2011, pp. 159-167. doi:10.1016/B978-0-12-396534-9.00009-X
- G. B. Whitham, “Linear and Nonlinear Wave,” John Wiley and Son Inc., Hoboken, 1999. doi:10.1002/9781118032954
- M. Aguero and R. Alvarado, “Bright and Singular Solitons in the Boussinesq Like Equation,” Physica Scripta, Vol. 62, No. 4, 2000, pp. 232-237. doi:10.1238/Physica.Regular.062a00232
- V. G. Makhankov, “Soliton Phenomenology,” Kluwer Academic Publishers, Dordrecht, 1990. doi:10.1007/978-94-009-2217-4
- P. Rosenau and J. M. Hyman, “Compactons: Solitons with Finite Wavelength,” Physical Review Letters, Vol. 70, No. 5, 1993, pp. 564-567. doi:10.1103/PhysRevLett.70.564
- A. L. Bertozzi and M. Pugh, “The Lubrication Approximation for Thin Viscous Films: Regularity and LongTime Behavior of Weak Solutions,” Communications on Pure and Applied Mathematics, Vol. 49, No. 2, 1996, pp. 85-123. doi:10.1002/(SICI)1097-0312(199602)49:2<85::AID-CPA1>3.0.CO;2-2
- M. Aguero, V. Serkin and T. Belyaeva, “Compacton Anti-Compacton Pair for Hydrogen Bonds and Rotational Waves in Dna Dynamics,” Communications in Nonlinear Science and Numerical Simulation, Vol. 16, No. 8, 2011 pp. 3071-3080. doi:10.1016/j.cnsns.2010.10.025
- R. H. J. Grimshaw, L. A. Ostrovsky, V. I. Shrira and Y. A. Stepanyants, “Long Nonlinear Surface and Internal Gravity Waves in a Rotating Ocean,” Surveys in Geophysics, Vol. 19, No, 4, 1998, pp. 289-338. doi:10.1023/A:1006587919935
- S. Dusuel, P. Michaux and M. Remoissenet, “From Kinks to Compactonlike Kinks,” Physical Review E, Vol. 57, No. 2, 1998, pp. 2320-2326. doi:10.1103/PhysRevE.57.2320
- B. Mihaila, et al., “Stability and Dynamical Properties of Rosenau—Hyman Compactons Using Pade Approximants,” Physical Review E, Vol. 81, No. 5, 2010, p. 056708. doi:10.1103/PhysRevE.81.056708

