International Journal of Modern Nonlinear Theory and Application
Vol.2 No.1A(2013), Article ID:29407,4 pages DOI:10.4236/ijmnta.2013.21A009
Branch Dynamics: A Theoretical Interpretation of Natural Phenomena
School of Information Management, Nanjing University, Nanjing, China
Email: yye@nju.edu.cn
Received October 27, 2012; revised December 10, 2012; accepted December 21, 2013
Keywords: Branch; Branch Dynamics; Gene Dynamics; Quaternion Physics; Natural Mechanism
ABSTRACT
The mechanism of natural branching is explored, which is characterized by branch dynamics, where interior dynamics and exterior dynamics reveal the unified mechanism of physical and biological phenomena. While interior dynamics is characterized by gene-interaction, gene-interchange and gene-interpretation via the quaternion mathematical processes of Cayley-Dickson branching, Grassman branching and Euclidian branching, exterior dynamics is characterized by multi-vector physical unification. Everything in the world is linked by branches, and the dynamic mechanism of the branching phenomena is approached by branch dynamics.
1. Introduction
The phenomenon of branching is omnipresent in our world. We can see branches anywhere, whether in the cosmos or in bio-organisms, in mountains, rivers, trees, fingers and blood vessels. Everything develops with branches. Branching is a general natural process in the world, reflecting the unity of the nature. So, branches should be brought into our thinking about physical reality [1].
Let us begin with quaternion and multi-vector mathematical methodology for describing branches.
2. Mathematical Foundations and the Structure of Branches
When we choose a quaternion basis {1, i, j, k}, there are

and
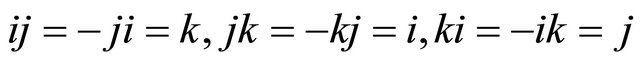 .
.
Then a quaternion q is denoted by
 (1)
(1)
Equation (1) can also be written as the form of dual complexes
 (2)
(2)
when we introduce a scalar function 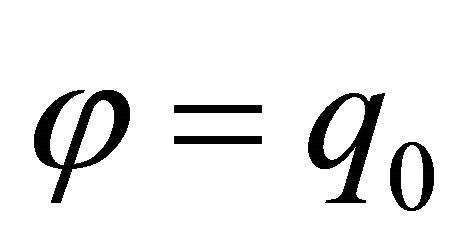 and a vector function
and a vector function , Equation (1) can be also recorded as a scalar-vector construction of quaternion
, Equation (1) can be also recorded as a scalar-vector construction of quaternion
 (3)
(3)
And when we record Equation (1.4) as
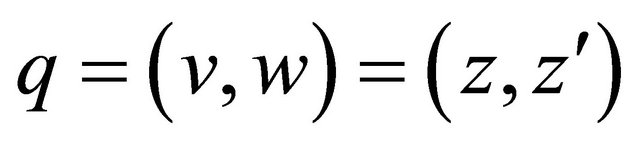 (4)
(4)
it is a Cayley-Dickson construction [2].
So, there exist scalar-vector branching and CayleyDickson branching in quaternion and we can call the branches a Hamilton representation of a quaternion, which guides us into the branch world.
Meanwhile, there is multi-vector Mk (k = 0, 1, 2, 3, 4), where Mk is a multi-vector of grade k. k = 0 is scalar, k = 1 vector, k = 2 bivector, k = 3 pseudovector and k = 4 pseudoscalar [3-5] as
 (5)
(5)
in which Ψ = φ – iθ constructs a complex wave function of matter, while A = V – iU forms a complex vector function of matter particles in space-time and F maintains a bivector as interaction. Equation (5) means that matter combines wave function and vector function with their interaction, which is an image fitting the duality of waveparticle, within the concept of combining mass and energy as matter.
The conjuncture of M is
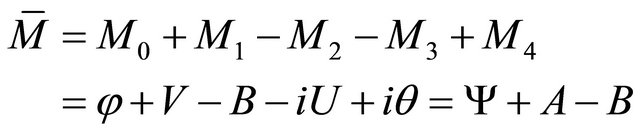 (6)
(6)
M can be divided into two parts, even M, M+, as left M, ML, and odd M, , as right M, MR:
, as right M, MR:
 (7)
(7)
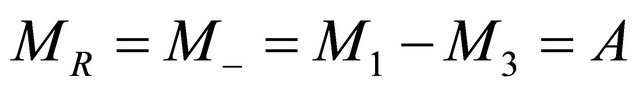 (8)
(8)
The reversion of multi-vector M, denoted by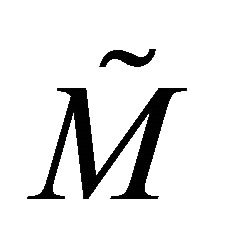 , can be defined as
, can be defined as
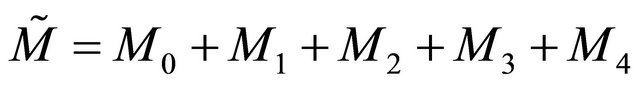 (9)
(9)
In order to describe the branching process, quaternion and multi-vector mathematics are suitable. When we combine quaternionic algebra, geometric algebra and calculus, the mathematical structure for branch dynamics will become apparent.
Suppose R, C, and H denote respectively real, complex, and quaternion fields. For a complex 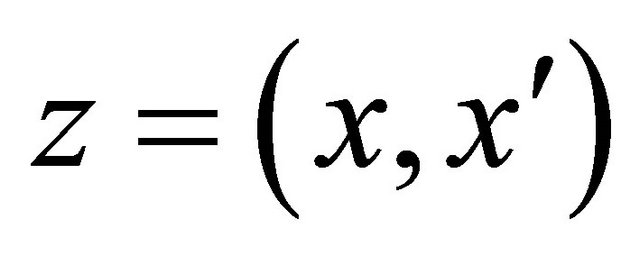 with
with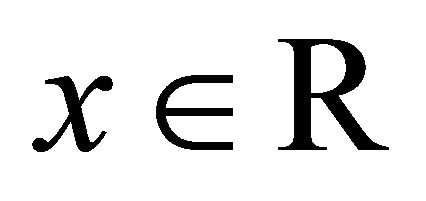 , record
, record  and
and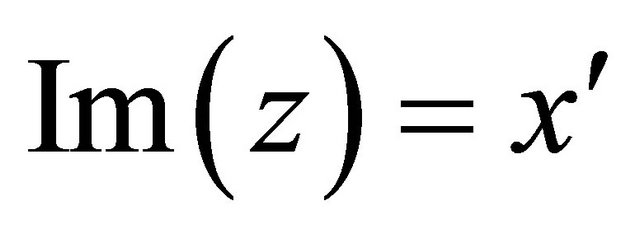 , called the real part and imaginary part respectively. And for a quaternion
, called the real part and imaginary part respectively. And for a quaternion 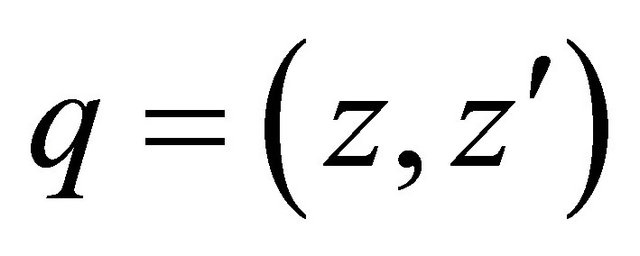 with
with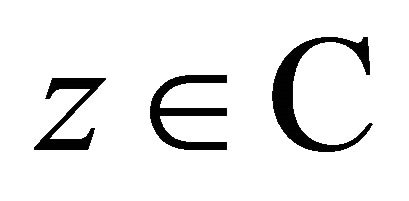 , record
, record  and
and , called the real or scalar part and vector or pure quaternion part respectively.
, called the real or scalar part and vector or pure quaternion part respectively.
While a quaternion (q) can be expressed by the scalar-vector construction and the Cayley-Dickson construction, there is a conjugation of q
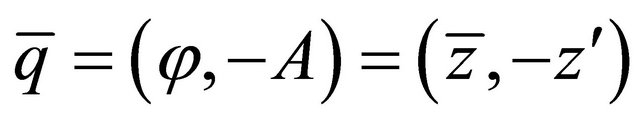 (10)
(10)
with  and norm
and norm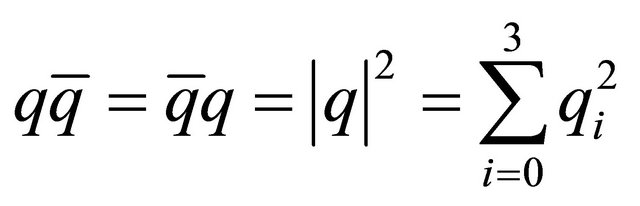 . Then we have
. Then we have
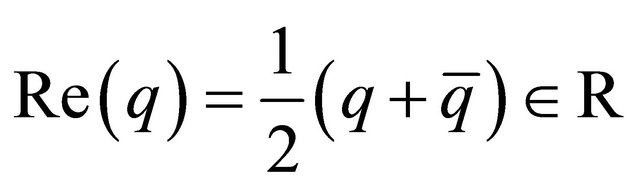 (11)
(11)
and
 (12)
(12)
where 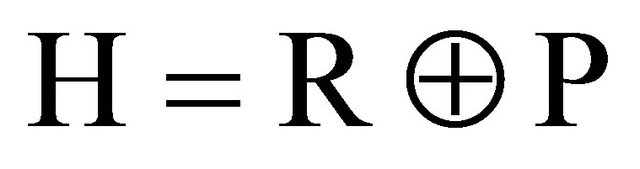 and P constructs 3-dimentional Euclidean vector space.
and P constructs 3-dimentional Euclidean vector space.
Using Pauli matrices and Dirac spinors [6-8], we know that a quaternion can split into 2 × 2 complex matrices by substitution 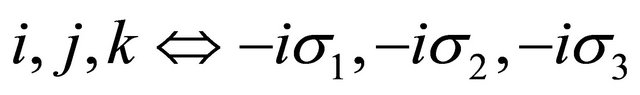 [9], where
[9], where  are the standard complex Pauli matrices as follows (together with unit matrix
are the standard complex Pauli matrices as follows (together with unit matrix )
)
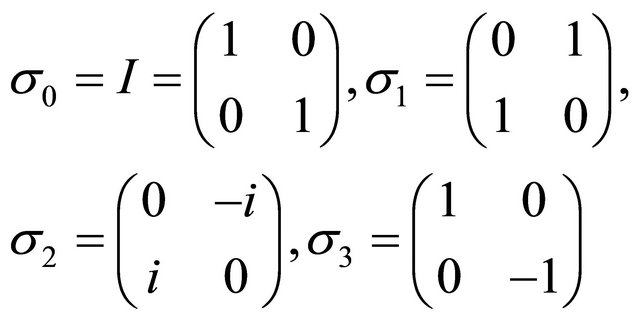 (13)
(13)
and Dirac matrices become
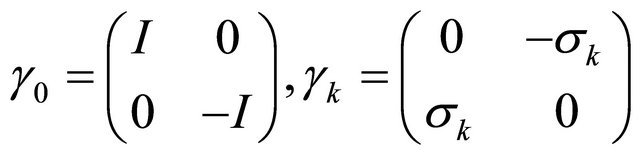 (14)
(14)
in which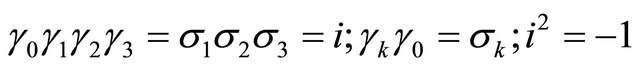 .
.
So, a quaternion has an equivalent representation which we can call the Pauli representation as
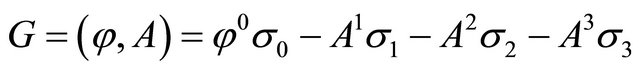 (15)
(15)
We see that Equation (15) is the same as the conjugation of q, Equation (10), as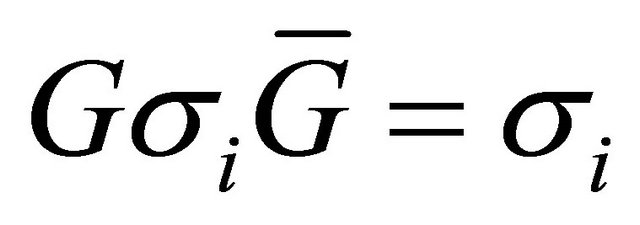 , which means that the Pauli representation and Hamilton representation become conjugations of each other. The algebraic structure shows that the Hamilton representation and Pauli representation exist naturally for a quaternion, which constructs a conjugation pair.
, which means that the Pauli representation and Hamilton representation become conjugations of each other. The algebraic structure shows that the Hamilton representation and Pauli representation exist naturally for a quaternion, which constructs a conjugation pair.
In the Hamilton representation, there are a CayleyDickson branch, a Grassman branch and a Euclidian branch, in which the Cayley-Dickson branch is produced by the multiplication of quaternion G1 and quaternion G2 with the form of the dual complex function form as
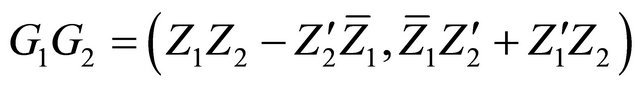 (16)
(16)
The Grassman branch produced by the multiplication of quaternion G1 and quaternion G2 with the form of scalar-vector representation as left branch
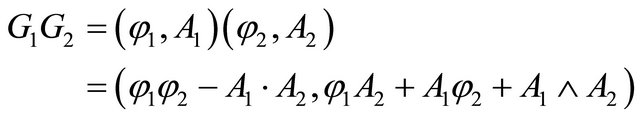 (17)
(17)
and a similar Euclidian branch as right branch
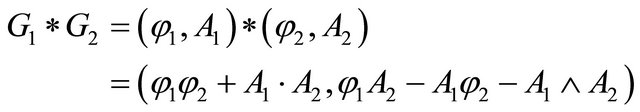 (18)
(18)
Noncommutative associative quaternion algebra provides rich algebraic branch structures, which establishes the foundations of branching. And a similar structure could be broadened to octonion (both quaternion algebra and octonion algebra belong to Clifford algebra), if we abandoned the associative property and then got only the alternative algebraic structure.
For multi-vector M, the frame basis can be unified in geometric algebra, spanned by

And for multi-vectors M and N, the geometric product is defined as
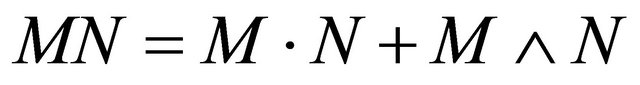 (19)
(19)
where. means inner product and ![]() outer product.
outer product.
3. Interior Dynamics of Branches
Using the idea of genes, if there are two quaternion genes G1 and G2 in a physical or biological system, with the following forms
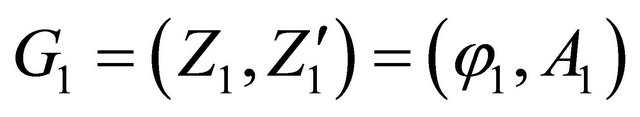 ,
, 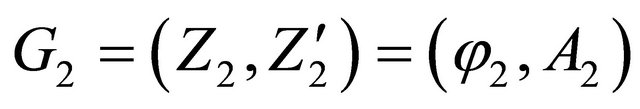 (20)
(20)
where we can call φi information functions and Ai potential functions (i = 1,2), their algebraic branches will construct their interior dynamics. This process (called 3I) includes the following steps.
3.1. Gene Interaction
A multiple of two genes will produce a Cayley-Dickson branch, a Grassman branch, and a Euclidian branch.
The Cayley-Dickson branch determines the mainstem:
 (21)
(21)
A scalar-vector branch produces various branches, and new genes will be produced when information functions and quality-quantity functions interact in a Grassman branch
 (22)
(22)
and a Euclidian branch:
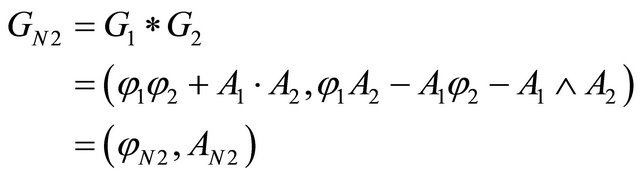 (23)
(23)
3.2. Gene Interchange
The combination or mutation of two genes will also produce new genes such as
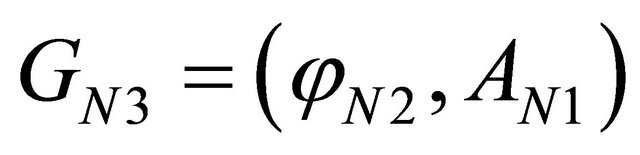 ,
,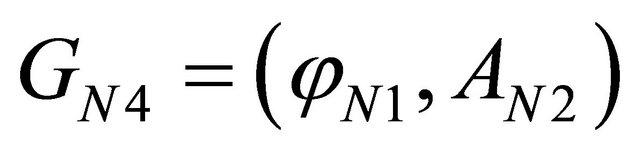 (24)
(24)
3.3. Gene Interpretation
A gene may develop or represent in time-space (t, s) and interact with its environment. During this process, fractals will be generated at the ends.
When genes and time-space are present, a physical body will be generated naturally. This is a unified interior mechanism of nature.
4. Exterior Dynamics of Branches
Synthesizing mathematical quaternion and multi-vector and physical theories [10-12], the world is described by notations
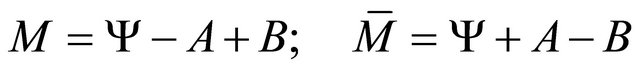 (25)
(25)
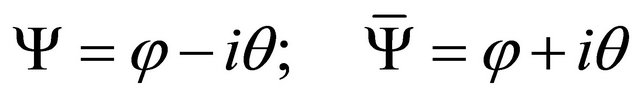 (26)
(26)
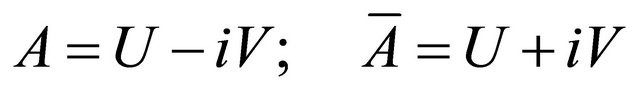 (27)
(27)
and
 (28)
(28)
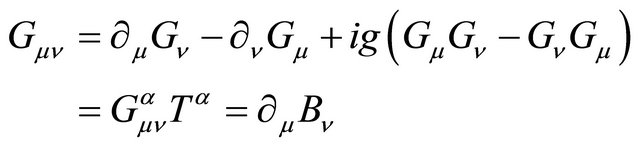 (29)
(29)
Keeping the local gauge invariance of physical laws, we know
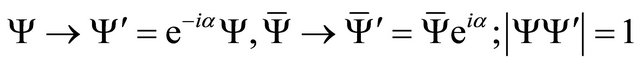 (30)
(30)
 (31)
(31)
 (32)
(32)
where R means Lorentz rotation and matrix UU–1 = I.
When the left branch is driven by M+ = Ψ – B and right branch by 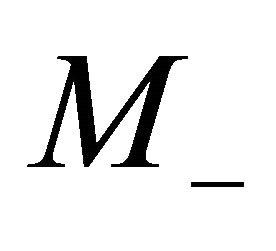 = A and Ψ = φ – iθ and A are linked by following equation
= A and Ψ = φ – iθ and A are linked by following equation
 (33)
(33)
we see that the exterior dynamics is mastered by
 (34)
(34)
and
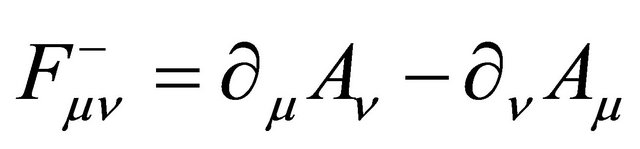 (35)
(35)
so the system Lagrangians become
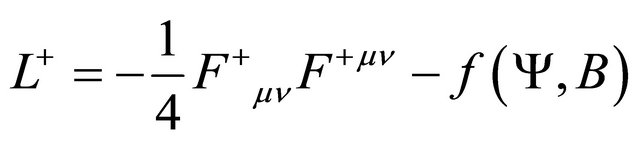 (36)
(36)
 (37)
(37)
As action 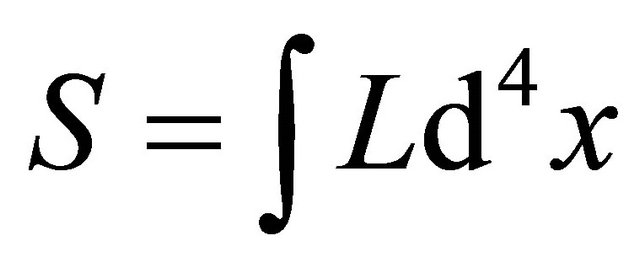 and
and , one knows dynamical mechanism.
, one knows dynamical mechanism.
5. Branch Dynamics of the Physical and Biological World
Branch dynamics can naturally produce physical and biological branching in cases where two genes act with each other in quaternion space-time. Via the main-stem process of gene-interaction, gene-interchange and gene-interpretation in interior dynamics, various branches are generated and form fractals at the ends. When left and right branching are controlled by physics, exterior developing can be naturally formed.
5.1. Two Branching
When interior genes are mastered by gene functions Gi and Gj, it will produce a Grassman branch
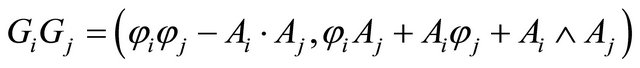 (38)
(38)
and a Euclidian branch
 (39)
(39)
At present, whether exterior development is dominated by left or right action, two branching will be produced. The two branches form a basic branch structure in the world, both physically and biologically. Obviously, left and right branches will not be complete symmetry.
5.2. Multi-Branching
Because there are different environments, complete symmetry seldom happens in nature, even if the same gene drives interior development. Furthermore, according to above branching ideas, no complete symmetry could happen in multi-branching. Different genes and different environments will introduce different branching, while genes decide interior processes and physical laws control exterior forms.
6. Concluding Remarks
Branch dynamics may be a valuable scientific exploration, as branches are basic general phenomena that have had no theory to explain them before. Quaternion and multi-vector mathematics provides good explanations of branch structures and reveals the interior mechanism of gene branch dynamics. And physical laws could explain exterior dynamics and interactions with environments. So it appears that branch dynamics is a good theoretical framework for interpretation of physical and biological branching phenomena. However, this paper only introduces a basic framework, in which information in gene functions determines interior dynamics, and the structure of time-space and distribution of matter-energy determine exterior dynamics. These physical ideas could be further researched in the future, as branch dynamics reveals a unified mechanism of nature while it also introduces a general framework for understanding the cosmos, so that we should clarify details about what happens within various branches. When we understand the branching mechanism, we extend our knowledge about various branches of natural phenomena.
7. Acknowledgements
The author is grateful to Ms. Regina P. Entorf at Wittenberg University in the US for her assistance with English wording.
REFERENCES
- R. Penrose, “The Road to Reality: A Complete Guide to the Laws of the Universe,” Jonathan Cape, London, 2004.
- J. C. Baez, “The Octonions,” 2004.
- D. Hestenes and G. Sobczyck, “Geometric Algebra to Geometric Calculus,” Reidel, Boston, 1984. doi:10.1007/978-94-009-6292-7
- C. J. L. Doran and A. N. Lasenby, “Geometric Algebra for Physicists,” Cambridge University Press, Cambridge, 2003. doi:10.1017/CBO9780511807497
- A. Lasenby, C. Doran and S. Gull, “Gravity, Gauge Theories and Geometric Algebra,” Philosophical Transactions of the Royal Society of London A, Vol. 356, No. 1737, 1998, pp. 487-582.
- A. Sudbery, “Quaternionic Analysis,” Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 85, 1979, pp. 199-225. doi:10.1017/S0305004100055638
- C. A. Deavours, “The Quaternion Calculus,” The American Mathematical Monthly, Vol. 80, No. 9, 1973, pp. 995- 1008. doi:10.2307/2318774
- K. Morita, “Quaternions, Lorentz Group and the Dirac Theory,” Progress of Theoretical Physics, Vol. 117, No. 3, 2007, pp. 501-532. doi:10.1143/PTP.117.501
- S. De Leo, “Quaternions for GUTs,” International Journal of Theoretical Physics, Vol. 35, No. 9, 1996, pp. 1821- 1837. doi:10.1007/BF02302418
- S. L. Alder, “Quarternionic Quantum Field Theory,” Communications in Mathematical Physics, Vol. 104, No. 4, 1986, pp. 611-656. doi:10.1007/BF01211069
- F. Y. Ye, “A Clifford-Finslerian Physical Unification and Fractal Dynamics,” Chaos, Solitons and Fractals, Vol. 41, No. 5, 2009, pp. 2301-2305. doi:10.1016/j.chaos.2008.09.004
- A. Connes, “Noncommutative Geometry and Reality,” Journal of Mathematical Physics, Vol. 36, No. 11, 1995, pp. 6194-6231. doi:10.1063/1.531241

