Open Journal of Fluid Dynamics
Vol.05 No.04(2015), Article ID:61670,7 pages
10.4236/ojfd.2015.54030
Effect of Curvature of Tip and Convexity of Electrode on Localization of Particles
Sudarshan Ghonge1, D. Nagendra Prasad1, Swarnim Narayan1, Hains Francis1, Astha Sethi2, Subimal Deb3, Souri Banerjee1
1Department of Physics, Birla Institute Technology and Science-Pilani, Hyderabad Campus, Hyderabad, India
2Department of Physics and Frederick Seitz Materials Research Laboratory, University of Illinois, Urbana-Champaign, IL, USA
3Department of Physics, GIT, GITAM University, Visakhapatnam, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 9 October 2015; accepted 30 November 2015; published 3 December 2015

ABSTRACT
We investigate the effect of curvature of the tip and the convexity of an electrode on the localization of suspended particles under the combined effect of dielectrophoresis and AC electroosmosis through simulations using COMSOL Multiphysics. A systematic analysis of the parameters defining the convexity of the electrode―the radius of the tip and the apex angle shows that suspended particles can be trapped closely to the electrode edges for comparatively larger tip radii and apex angles. This in turn should favour the trapping of polarizable molecules between the electrodes only if the fluid velocities at the vortices are not very strong.
Keywords:
Finite Element Method, Transport Dynamics, AC Electroosmosis, Dielectrophoresis, Vortex

1. Introduction
The manipulation of polarizable biomolecules like DNA by electrical forces in microdevices has become a topic of increasing interest as it finds wide-spread applications in lab-on-a-chip technology or in DNA diagnostics [1] . In a suitable condition, a DNA molecule in an electrolytic solution will develop a strong electric dipole moment [2] . This induced dipole allows trapping and manipulation of the molecule when placed within micro-electrodes owing to a process known as dielectrophoresis (DEP) [3] [4] . In this context it is worth mentioning that the dielectrophoretic motion of DNA molecules requires alternate current (AC) electric field to suppress the electrophoric effect of the molecules’ net charge [5] . However, the motion of the DNA molecules and hence their trapping/manipulation possibilities within a set of microelectrodes will also be countered by the flow of the electrolyte known as AC electro-osmosis (ACEO) [6] . Thus balancing DEP and ACEO is found to be a promising technique to study non-contact manipulation/trapping of DNA molecules suspended in an electrolyte solution and placed within electrically fed microelectrodes [7] . Washizu et al. [8] used a set of interdigitated sinusoidally corrugated aluminum microelectrodes to experimentally observe site-specific immobilization of double-stranded DNA molecules under AC electric field and concluded that the orientation of DNA molecules depended strongly on the electric field strength. Similar interdigitated rectangular metal microelectrodes of different dimensions and gap lengths were later investigated, both experimentally and numerically, by several researchers [9] in order to understand movement of DNA molecules within microelectrodes under electrokinetic effects. From these studies it appears that one might further exploit state-of-art lithographic technique to fabricate smaller electrodes with sharper bends which would intensify the non-uniformity of electric field and significantly influence DNA manipulation. To this end, use of triangular shaped electrodes has recently been very popular [10] [11] . Porath et al. [10] reported the first experimental evidence of trapping of a single, double stranded DNA molecule between the two vertices of a set of triangular electrodes where a few nanometers were apart. It clearly revealed that electric field strength which was extremely large at the vertices of the triangular electrode, coupled with polarization properties, played an important role in guiding the flow of DNA molecules in and around the tips. However, the most modern lithographic technique has its limitation to reproduce the bends or sharpness of the electrodes [11] . Thus it is interesting to study how small variations in electrode configurations would affect the nature of immobilization of the suspended DNA molecules confined between them.
In this report, we present a systematic analysis of the effect of curvature of the electrode tips on the localization of insoluble particles. We have also tried to assess how the convexity of the electrodes could influence the localization process.
2. Theory
The system under consideration consisting of two triangular electrodes is schematically represented in Figure 1. The vertices of the triangular electrodes are rounded as would be in the case of an actual fabrication. The rounded vertex results in a lower gradient of electric field around the tip in contrast to sharp vertices. We shall call the radius
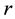 of the rounded electrode corner (represented by a dashed circle) the fillet radius. The vertex angle
of the rounded electrode corner (represented by a dashed circle) the fillet radius. The vertex angle
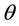 (acute angle between the electrode edges) defines the convexity of the electrodes. An increase in
(acute angle between the electrode edges) defines the convexity of the electrodes. An increase in
 keeping
keeping
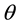 constant would result in electrodes with blunter tips with the same convexity. This is to match a practical scenario where lithographic tools are used to fabricate microlectrodes [11] . Such a pair of electrodes placed at the base of a cubical region filled with an electrolyte, is studied numerically for the possibility of localization of suspended particles.
constant would result in electrodes with blunter tips with the same convexity. This is to match a practical scenario where lithographic tools are used to fabricate microlectrodes [11] . Such a pair of electrodes placed at the base of a cubical region filled with an electrolyte, is studied numerically for the possibility of localization of suspended particles.
The properties of the electrolyte used for this configuration correspond to that of KCl at infinite dilution with electrical conductivity of 0.0021 S/m, relative permittivity of 78.49, density of 1000 kg/m3 and a dynamic viscosity (at 293 K) of 0.001 Pa-s [12] .
We consider the variation of the apex angle with a fixed separation ( ) between the tips of the electrode. The
) between the tips of the electrode. The
Figure 1. Schematic representation of the top view of the electrode setup. The dashed lines along
 and
and
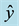 represent the planes of mirror symmetry transverse to the plane of the electrodes.
represent the planes of mirror symmetry transverse to the plane of the electrodes.
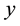 -
-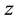 plane, a plane of mirror symmetry between the electrodes, reduces the domain of the problem by half owing to the symmetry of the configuration and opposite polarities of the electrodes. Clearly an obtuse apex angle is a concave configuration of the electrode edges facing each other. Convex electrodes produce the strongest electric fields near their apices owing to the proximity of the tips. This produces a region of strong electric field at the center of the configuration that gradually decreases away from the origin along the y-axis on either side. A concave electrode, on the other hand, has a gradually decreasing spacing between the edges (measured along the x-axis) which produces a field of least strength at the origin, gradually increasing along the positive and negative y-axis. Changing the apex angle from acute to obtuse is a cross-over from the first regime of the electric field decreasing away from the origin to the one where the field density change is reversed. We cover both the regimes by changing the apex angle.
plane, a plane of mirror symmetry between the electrodes, reduces the domain of the problem by half owing to the symmetry of the configuration and opposite polarities of the electrodes. Clearly an obtuse apex angle is a concave configuration of the electrode edges facing each other. Convex electrodes produce the strongest electric fields near their apices owing to the proximity of the tips. This produces a region of strong electric field at the center of the configuration that gradually decreases away from the origin along the y-axis on either side. A concave electrode, on the other hand, has a gradually decreasing spacing between the edges (measured along the x-axis) which produces a field of least strength at the origin, gradually increasing along the positive and negative y-axis. Changing the apex angle from acute to obtuse is a cross-over from the first regime of the electric field decreasing away from the origin to the one where the field density change is reversed. We cover both the regimes by changing the apex angle.
The special case of plane parallel electrodes (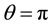 ) exhibits two symmetries. The first is a translational symmetry along the edge of the electrodes. The second is a mirror symmetry about the y-z plane through the origin. The mirror symmetry warrants the use of the method of images under an applied electric potential and reduces the problem space by half. The translational symmetry reduces the configuration to two dimensions confined to the plane of translational symmetry. This configuration was studied in detail by Green et al. [13] .
) exhibits two symmetries. The first is a translational symmetry along the edge of the electrodes. The second is a mirror symmetry about the y-z plane through the origin. The mirror symmetry warrants the use of the method of images under an applied electric potential and reduces the problem space by half. The translational symmetry reduces the configuration to two dimensions confined to the plane of translational symmetry. This configuration was studied in detail by Green et al. [13] .
The arrangement of triangular electrodes has two planes of mirror symmetry in the arrangement: the first being the x-z plane passing through the apex of both the electrodes; the second being the y-z plane through the origin. This space, however, must be studied as a three-dimensional system since the convexity of the electrodes breaks the translational symmetry that existed for . The three parameters for our study could be
. The three parameters for our study could be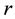 ,
,
 and
and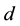 , where one could systematically vary a parameter holding the other two fixed. Here we present the simulation studies with varying
, where one could systematically vary a parameter holding the other two fixed. Here we present the simulation studies with varying




We use




where




where the Clausius-Mossotti factor

Here






The radius of the Lambda DNA is known to be in the range 2 to 4 μm. A similar study by Bown and Meinhart [16] on the DNA of Lambda phage bacteria was reported in a frequency range of 100 Hz to 1.6 MHz with a rotationally symmetric electrode configuration. The expression for the DEP force on a particle, also given by an alternate expression [3] , provides a measure of the effective polarizability of the particle and the magnitude of the electric field, which has been used in earlier simulations [17] and the formula as given by Equation 3 is found suitable to calculate DEP forces for spherical particles [15] . Washizu and Kurosawa [2] have shown that the DNA would stretch under an electric field. Stretching the DNA can result in a change of the effective polarizability of the molecule resulting in a shift of the trapping points. Regtmeier et al. [18] have reported that the polarizability of the DNA in linear and supercoiled forms is of similar magnitude within error margins. We therefore use the same effective polarizability for free and trapped particles assuming that the stretched DNA (under the applied field) will not affect the trapping points.
3. Results and Discussion
We use a particle size of














3.1 Variation of Apex Angle
A variation of





Figure 3 shows the variation of the slope (stiffness) of the



Figure 2. Variation of the x-component of the force on a stretched DNA molecule along the x-axis. The specific param- eters used are


Figure 3. Variation of the slope of the x-component of the force as a function of the apex angle

reflex angle, and therefore, the two plots in Figure 3 are consistent with each other. Smaller slope (stiffness) at larger

3.2 Variation of Apex Radius
A variation of the fillet radius













4. Conclusion
In conclusion, we have systematically analyzed two of the three parameters (the fillet radius and the apex angle) that may be tuned to have a localizing region for suspended DNA molecules in electrolytes. It is found that stiffness of the force decreases with increase of the apex angle, indicating weaker trapping sites in the electrolyte as the convexity of the electrode increases. In this context we tried to address a practical situation where electrodes of fixed and moderate convexity but having different curvature of the tips were considered. Our study reveals that the strength of the vortex gets weaker and its span becomes wider as the tip gets more and more rounded. It also provides an intuitive insight that, if polarization of DNA molecules has any role to facilitate the DNA attachment process, it is desirable to have vortex of moderate strength and span around the edge of the electrode such that the molecules are localized (rather than being strongly trapped) in the vortex facilitating polarization to complete the bridging process. Therefore, it is suggested that a set of electrodes with fixed convexity but having rounded tips may better serve the purpose of bridging electrodes by DNA molecules. It would be

Figure 4. Variation of the (a) slope, (b) strength and (c) span of the


interesting to further study the strength, distribution and the span of vortex points within the electrolyte as a function of electrode separation as well (keeping


Acknowledgements
One of the authors (SB) acknowledges the financial support of the Board of Research in Nuclear Sciences, Department of Atomic Energy, Govt. of India for financial assistance.
Cite this paper
SudarshanGhonge,D. NagendraPrasad,SwarnimNarayan,HainsFrancis,AsthaSethi,SubimalDeb,SouriBanerjee, (2015) Effect of Curvature of Tip and Convexity of Electrode on Localization of Particles. Open Journal of Fluid Dynamics,05,295-301. doi: 10.4236/ojfd.2015.54030
References
- 1. Abramowitz, S. (1996) Towards Inexpensive DNA Diagnostics. Trends in Biotechnology, 14, 397-401.
http://dx.doi.org/10.1016/0167-7799(96)10051-2 - 2. Washizu, M. and Kurosawa, O. (1990) Electrostatic Manipulation of DNA in Microfabricated Structures. IEEE Transactions on Industry Applications, 26, 1166-1172.
http://dx.doi.org/10.1109/28.62403 - 3. Pohl, H.A. (1978) Dielectrophoresis: The Behavior of Neutral Matter in Nonuniform Electric Fields. Cambridge University Press, Cambridge.
- 4. Asbury, C.L. and van den Engh, G. (1998) Trapping of DNA in Nonuniform Oscillating Electric Fields. Biophysical Journal, 74, 1024-1030.
http://dx.doi.org/10.1016/s0006-3495(98)74027-5 - 5. Bakewell, D.J. and Morgan, H. (2006) Dielectrophoresis of DNA: Time- and Frequency-Dependent Collections on Microelectrodes. IEEE Transactions on Nano Bioscience, 5, 1-8.
- 6. Loucaides, N.G., Ramos, A. and Georghiou, G.E. (2008) Trapping and Manipulation of Nanoparticles by Using Jointly Dielectrophoresis and AC Electroosmosis. Journal of Physics: Conference Series, 100, Article ID: 052015.
http://dx.doi.org/10.1088/1742-6596/100/5/052015 - 7. Du, J.-R., Juang, Y.-J., Wu, J.-T. and Wei, H.-H. (2008) Long-Range and Superfast Trapping of DNA Molecules in an AC Electrokinetic Funnel. Biomicrofluidics, 2, Article ID: 044103.
http://dx.doi.org/10.1063/1.3037326 - 8. Washizu, M., Kurosawa, O., Arai, I., Suzuki, S. and Shimamoto, N. (1995) Applications of Electrostatic Stretch-and-Positioning of DNA. IEEE Transactions on Industry Applications, 31, 447-456.
http://dx.doi.org/10.1109/28.382102 - 9. Asbury, C.L., Diercks, A.H. and van den Engh, G. (2002) Trapping of DNA by Dielectrophoresis. Electrophoresis, 23, 2658-2666.
http://dx.doi.org/10.1002/1522-2683(200208)23:16<2658::aid-elps2658>3.0.co;2-o - 10. Porath, D., Bezryadin, A., De Vries, S. and Dekker, C. (2000) Direct Measurement of Electrical Transport through DNA Molecules. Nature, 403, 635-638.
- 11. Zheng, L.F., Brody, J.P. and Burke, P.J. (2004) Electronic Manipulation of DNA, Proteins, and Nanoparticles for Potential Circuit Assembly. Biosensors and Bioelectronics, 20, 606-619.
http://dx.doi.org/10.1016/j.bios.2004.03.029 - 12. Ramos, A., Morgan, H., Green, N.G. and Castellanos, A. (1998) AC Electrokinetics: A Review of Forces in Microelectrode Structures. Journal of Physics D: Applied Physics, 31, 2338.
http://dx.doi.org/10.1088/0022-3727/31/18/021 - 13. Green, N.G., Ramos, A., Gonzalez, A., Morgan, H. and Castellanos, A. (2002) Fluid Flow Induced by Nonuniform AC Electric Fields in Electrolytes on Microelectrodes. III. Observation of Streamlines and Numerical Simulation. Physical Review E, 66, Article ID: 026305.
http://dx.doi.org/10.1103/PhysRevE.66.026305 - 14. Comsol 4.3a. http://www.comsol.com
- 15. Green, N.G. and Morgan, H. (1997) Dielectrophoretic Investigations of Sub-Micrometre Latex Spheres. Journal of Physics D: Applied Physics, 30, 2626.
http://dx.doi.org/10.1088/0022-3727/30/18/018 - 16. Bown, M.R. and Meinhart, C.D. (2006) AC Electroosmotic Flow in a DNA Concentrator. Microfluidics and Nanofluidics, 2, 513-523.
http://dx.doi.org/10.1007/s10404-006-0097-4 - 17. Tuukkanen, S., Kuzyk, A., Toppari, J.J., Hakkinen, H., Hytonen, V.P., Niskanen, E., Rinkio, M. and Torma, P. (2007) Trapping of 27 bp - 8 kbp DNA and Immobilization of Thiol-Modified DNA Using Dielectrophoresis. Nanotechnology, 18, Article ID: 295204.
http://dx.doi.org/10.1088/0957-4484/18/29/295204 - 18. Regtmeier, J., Eichhorn, R., Bogunovic, L., Ros, A. and Anselmetti, D. (2010) Dielectrophoretic Trapping and Polarizability of DNA: The Role of Spatial Conformation. Analytical Chemistry, 82, 7141-7149.
http://dx.doi.org/10.1021/ac1005475






