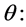Received 28 March 2015; accepted 8 March 2016; published 11 March 2016

ABSTRACT

This paper examined the hydromagnetic boundary layer flow of viscoelastic fluid with heat and mass transfer in a vertical channel with rotation and Hall current. A constant suction and injection is applied to the plates. A strong magnetic field is applied in the direction normal to the plates. The entire system rotates with uniform angular velocity (W), about the axis perpendicular to the plates. The governing equations are solved by perturbation technique to obtain an analytical result for velocity, temperature, concentration distributions and results are presented graphically for various values of viscoelastic parameter (K₂), Prandtl number (Pr), Schmidt number (Sc), radiation parameter (R), heat generation parameter (Qh) and Hall parameter (m).

Keywords:

Visco-Elastic Fluid, MHD, Hall Effect, Porous Medium

1. Introduction

Hydromagnetic convection with heat transfer in a rotating medium has important applications in geophysics, nuclear power reactors and in underground water and energy storage system. When the strength of the magnetic field is strong, one cannot neglect the effects of Hall currents. A comprehensive discussion of Hall current is given by Cowling [1] , Soundalgekar [2] , Soundalgekar and Uplekar [3] . Hossain and Rashid [4] analyzed Hall effect of MHD free convective flow along porous plate with mass transfer. Attia [5] studied Hall current on the velocity and temperature fields on unsteady Hartmann flow. Effects of Hall current on free convective flow past on accelerated vertical plate in a rotating system with heat source/sink is analyzed by Singh and Garg [6] . Saha et al. [7] studied Hall current effect on MHD natural convection from a vertical plate. Aboeldahad and Elbarbary [8] examined heat and mass transfer over a vertical plate in the presence of magnetic field and Hall effect. Abo-Eldahab and El Aziz [9] investigated the Hall current and Joule heating effects on electrically conducting fluid past a semi-infinite plate with strong magnetic field and heat generation/absorption. Radiation effects on free convection flow have become very important due to its applications in space technology, processes having high temperature and design of pertinent equipments. Moreover, heat and mass transfer with thermal radiation on convective flows is very important due to its significant role in the surface heat transfer. Recent developments in gas cooled nuclear reactors, nuclear power plants, gas turbines, space vehicles, and hypersonic flights have attracted research in this field. The unsteady convective flow in a moving plate with thermal radiation was examined by Cogley et al. [10] and Mansour [11] . The combined effects of radiation and buoyancy force past a vertical plate were analyzed by Hossain and Takhar [12] . Hossain et al. [13] analyzed the influence of thermal radiation on convective flows over a porous vertical plate. Seddeek [14] explained the importance of thermal radiation and variable viscosity on unsteady forced convection with an align magnetic field. Muthucumaraswamy and Senthil [15] studied the effects of thermal radiation on heat and mass transfer over a moving vertical plate. Pal [16] investigated convective heat and mass transfer in a stagnation-point flow towards a stretching sheet with thermal radiation. Aydin and Kaya [17] justified the effects of thermal radiation on mixed convection flow over a permeable vertical plate with magnetic field. Mohamed [18] studied unsteady MHD flow over a vertical moving porous plate with heat generation and Soret effect. Chauhan and Rastogi [19] analyzed the effects of thermal radiation, porosity and suction on unsteady convective hydromagnetic vertical rotating channel. Ibrahim and Makinde [20] investigated radiation effect on chemical reaction MHD boundary layer flow of heat and mass transfer past a porous vertical flat plate. Pal and Mondal [21] studied the effects of thermal radiation on MHD Darcy-Forchheimer convective flow past a stretching sheet in a porous medium. The study of heat and mass transfer due to chemical reaction is also very important because of its occurrence in most of the branches of science and technology. The processes involving mass transfer effects are important in chemical processing equipments which are designed to draw high value products from cheaper raw materials with the involvement of chemical reaction. In many industrial processes, the species undergo some kind of chemical reaction with the ambient fluid which may affect the flow behavior and the production quality of final products. Kandasamy et al. [22] discussed the effects of chemical reaction and magnetic field on heat and mass transfer over a vertical plate stretching surface. Muthu-cumaraswamy and Janakiraman [23] analyzed the effects of mass transfer over a vertical oscillating plate with chemical reaction. Sharma and Singh [24] have analyzed the unsteady MHD free convection flow and heat transfer over a vertical porous plate in the presence of internal heat generation and variable suction. Sudheer Babu and Satya Narayan [25] examined chemical reaction and thermal radiation effects on MHD convective flow in a porous medium in the presence of suction. Makinde and Chinyoka [26] studied the effects of magnetic field on MHD Couette flow of a third-grade fluid with chemical reaction. Recently, Pal and Talukdar [27] investigated the influence of chemical reaction and Joule heating on unsteady convective viscous dissipating fluid over a vertical plate in porous media with thermal radiation and magnetic field. Despite the above studies, attention has hardly been focused to study the effects of the Hall current on unsteady hydromagnetic non-Newtonian fluid flows. Such work seems to be important and useful partly for gaining a basic understanding of such flows and partly possible applications of these fluids in chemical process industries, food and construction engineering, movement of biological fluids. Another important field of application is the electromagnetic propulsion. The study of such system, which is closely associated with magneto-chemistry, requires a complete understanding of the equation of state shear stress-shear rate relationship, thermal conductivity and radiation. Some of these properties are undoubtedly influenced by the presence of an external magnetic field. Sarpkaya (1961) discussed the steady flow of a uniformly conducting non-Newtonian incompressible fluid between two parallel plates. The fluid considered is under the influence of constant pressure gradient. Aldos et al. [28] studied MHD mixed convection flow from a vertical plate embedded in porous medium. Rajgopal et al. [29] analyzed an oscillatory mixed convection flow of a viscoelastic electrically conducting fluid in an infinite vertical channel filed with porous medium. Considering the Hall effects Attia [30] discussed unsteady Hartmann flow of a viscoelastic fluid. Chaudhary and Jha [31] analyzed heat and mass transfer in elastic-viscous fluid past an impulsively started infinite vertical plate with Hall current. Singh [32] investigated MHD mixed convection visco-elastic slip-flow through a porous medium in a vertical porous channel with thermal radiation. The objective of the present study is to analyze the effects of Hall current, thermal radiation, and first-order chemical reaction on the oscillatory convective flow of viscoelastic fluid with suction/injection in a rotating vertical porous channel.

2. Mathematical Formulation

The constitutive equations for the rheological equation of state for an elastico-viscous fluid (Walter’s liquid B') are

. (1)

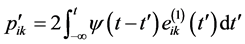. (2)

in which

. (3)

N(t) is the distribution function of relaxation times. In the above equations p_ik is the stress tensor, p an arbitrary isotropic pressure, g_ik is the metric tensor of a fixed co-ordinate system x_i and is the rate of strain tensor. It was shown by Walter’s [33] that Equation (2) can be put in the following generalized form which is valid for all types of motion and stress

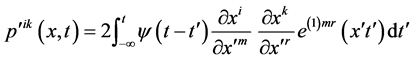(4)

where is the position at time t' of the element that is instantaneously at the print xⁱ at time “t”. The fluid with equation of state (1) and (4) has been designated as liquid B'. In the case of liquids with short memories, i.e. short relaxation times, the above equation of state can be written in the following simplified form

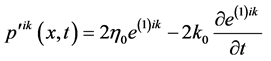. (5)

In which 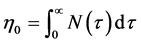is the limiting viscosity at small rates of shear, 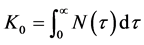and de-

notes the convected time derivative. We consider Oscillatory free convective flow of a viscous incompressible and electrically conducting fluid between two insulating infinite vertical permeable plates. A strong transverse magnetic field of uniform strength is applied along the axis of rotation by neglecting induced electric and magnetic fields. The fluid is assumed to be a gray, emitting, and absorbing, but non scattering medium. The radiative heat flux term can be simplified by using the Rosseland approximation. It is also assumed that the chemically reactive species undergo first-order irreversible chemical reaction.

The equations governing the flow of fluid together with Maxwell’s electromagnetic equations are as follows.

Equation of Continuity

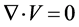. (6)

Momentum Equation

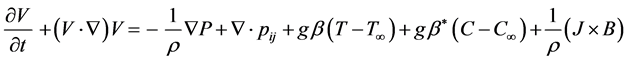. (7)

Energy Equation

. (8)

Concentration Equation

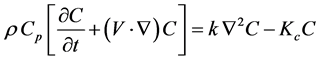. (9)

The generalized Ohm’s law, in the absence of the electric field [34] , is of the form.

(10)

where and p_e are velocity, the electrical conductivity, the magnetic permeability, the cyclotron frequency, the electron collision time, the electric charge, the number density of the electron and the electron pressure, respectively. Under the usual assumption, the electron pressure (for a weakly ionized gas), the thermoelectric pressure, and ion slip are negligible, so we have from the Ohm’s law.

. (11)

From which we obtain that

. (12)

The solenoidal relation for the magnetic field where gives (con-

stant) everywhere in the flow, which gives. If are the component of electric current density, then the equation of conservation of electric charge gives.

Since the plates are infinite in extent, all the physical quantities except the pressure depend only on and. A cartesian coordinate system is assumed and -axis is taken normal to the plates, while -axis and -axis are in the upward and perpendicular directions on the plate (origin), respectively .The velocity components, , are in the -, -, -directions respectively. The governing equations in the rotating system in presence of Hall current, thermal radiation and chemical reaction are given by the following equations.

(13)

(14)

(15)

(16)

(17)

where is the Hall parameter, and are coefficients of thermal and solutal expansion, c_p is the specific heat at constant pressure, is the density of the fluid, v is the kinematics viscosity k is the fluid thermal conductivity, is the acceleration of gravity, is the additional heat source, is the radiative heat flux, D_m is the molecular diffusivity, K₁ is the chemical reaction rate constant .The radiative heat flux is

given by, in which and are the Stefan-Boltzmann constant and the mean absorp-

tion coefficient, respectively.

The initial and boundary conditions as suggested by the physics of the problem are

(18)

where e is a small constant.

We now introduce the dimensionless variables and parameter as follows:

. (19)

After combining (14) and (15) and taking, then (14)-(17) reduce to

(20)

where is the modified Grashof number, is the Prandtl number,

is the modified solutal Grashof number, is the Hartmann

number, is the radiation parameter, is the Schmidt number, and is the reaction parameter.

The boundary conditions (9) can be expressed in complex form as:

. (21)

3. Method of Solution

The set of partial differential Equations (20) cannot be solved in closed form. So it is solved analytically after these equations are reduced to a set of ordinary differential equations in dimensionless form. We assume that

(22)

where R stands for q or or and which is applicable for small perturbation.

Substituting (22) into (20) and comparing the harmonic and non harmonic terms, we obtain the following ordinary differential equations:

(23)

where and dashes denote the derivatives w.r.t.

The Transformed boundary conditions are

. (24)

The solutions of (23) under the boundary conditions are

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

. (33)

3.1. Amplitude and Phase Difference Due to Steady and Unsteady Flow

Equation (25) corresponds to the steady part, which gives ₀ as the primary and V₀ as secondary velocity components. The amplitude (resultant velocity) and phase difference due to these primary and secondary velocities for the steady flow are given by

(34)

where

Equation (26) and (27) together give the unsteady part of the flow. Thus unsteady primary and secondary velocity components and, respectively, for the fluctuating flow can be obtained from the following.

. (35)

The amplitude (resultant velocity) and the phase difference of the unsteady flow are given by

(36)

where

The amplitude (resultant velocity) and the phase difference are given by

(37)

where u = Real part of q and v = Imaginary part of q.

3.2. Amplitude and Phase Difference of Shear Stresses Due to Steady and Unsteady Flow at the Plate

The amplitude and phase difference of shear stresses at the stationary plate (η = 0), the steady flow can be obtained as

. (38)

For the unsteady part of flow, the amplitude and phase difference of shear stresses at the stationary plate () can be obtained as.

where

(39)

(40)

where

. (41)

The amplitude and phase difference of shear stresses at the stationary plate (η = 0) can be as

(42)

where Real part of and Where Imaginary part of.

The Nusselt number

. (43)

The rate of heat transfer (i.e. heat flux) at the plate in terms of amplitude and phase difference is given by

. (44)

The Sherwood number

. (45)

The rate of mass transfer (i.e. mass flux) at the plate in terms of amplitude and phase difference is given by.

. (46)

4. Results and Discussion

The system of ordinary differential Equation (23) with boundary condition (24) is solved analytically using perturbation technique. The solutions are obtained for the steady and unsteady velocity fields from (25)-(27), temperature fields from (28)-(30) and concentration fields are given by (31)-(33). The influences of each of the parameters on the thermal mass and hydrodynamic behaviors of buoyancy-induced flow in a rotating vertical channel are studied. The results are presented graphically. Temperature of the heated wall (left wall) is a function of time as given in the boundary conditions and the cooled wall at is maintained at a constant temperature. Further it is assumed that the temperature difference is small enough so that the density changes of the fluid in the system will be small. When the injection/suction parameter l is positive, fluid is injected through the hot wall into the channel and sucked out through the cold wall. The effect of various physical parameters on flow, heat, concentration fields, skin-friction Nusselt number, and Sherwood number are presented graphically in Figures 1-14. The profiles for resultant velocity Rn for the flow are in Figures 1-4 for suction/injection parameter l, rotation parameter W, viscoelastic parameter K₂, and e respectively. Figure 1 shows that increase in the suction parameter l leads to an increase of Rn within the stationary plates. Similarly the

resultant velocity increases with increasing values of rotation parameter W. This is due to the fact that the rotation effects being more dominant near the walls, so when W reaches high values secondary velocity component v decreases with increases in W as shown in Figure 2. From Figure 3, it is observed that the increase in the e leads to an increase of Rn within the stationary plates. From Figure 4, it inferred that resultant velocity Rn goes on increasing with increasing value of viscoelastic parameter K₂.

The phase difference a for the flow is shown graphically in Figures 5-8. Figure 5 shows phase angle for various positive values of suction/injection parameter l. The figure shows that the phase angle a decreases with the increases of suction parameter. Figure 6 is the phase angle for various values of rotation parameter W. From this figure, it is observed that the phase angle a decreases with an increase in rotation parameter. From Figure 7, it is observed that the phase angle a increases with an increase in visco elastic parameter. Figure 8 shows the variation of a against h for different values of thermal Grashof number Gr, Solutal Grashof number Gm, and Hartmaan number. From this figure, it is found that the values of phase a decreases with increasing values of Gr, Gm and M while reversed effect is observed for the Hall parameter m.

The concentration profile f for the flow is shown graphically in Figure 9, Figure 10. From Figure 9, it is observed that with the increasing the value of the chemical reaction parameter decreases the concentration of species in the boundary layer; this due to the fact that destructive chemical reduces the solutal boundary thickness and increases the mass transfer. Opposite trend is seen in the case when Schmidt number is increased as noted in Figure 10. It may also be observed from this figure that the effect of Schmit number Sc is to be increases the concentration distribution in the solutal boundary layer.

The temperature profiles q are shown graphically in Figure 11 and Figure 12. Figure 11 has been plotted to depict the variation of temperature profiles against h for different values of heat absorption parameter Q_H by fixing other physical parameters. From this figure, we observe that temperature q decreases with increase in the heat absorption parameter Q_H because when heat is absorbed, the buoyancy force decreases the temperature profile. Figure 12 represents graph of temperature distribution with h for different values of radiation parameter. From this figure, we note that initial temperature q = 1 decreases zero satisfying boundary condition at h = 1.0 Further, it is observed from this figure that increase in the radiation parameter decreases the temperature distribution in the thermal boundary layer due to decreases in the thickness of the thermal boundary layer with thermal radiation parameter R. This is because large values of radiation parameter correspond to an increase in dominance of conduction over radiation, thereby decreasing the buoyancy force and temperature in the thermal boundary layer.

Figure 13 and Figure 14 show the amplitude of skin-friction, Nusselt number, and Sherwood number against frequency parameter w for different values of Q_H, and, respectively. The amplitude of Nusselt number decreases with increasing the value of heat source parameter Q_H which is shown in Figure 13. Figure 14 shows the variation of Sherwood number with and w. From this figure, it is observed that the Sherwood number decreases with increasing the value of chemical reaction parameter, and opposite trend is seen with increasing the values of w.

Cite this paper

Pradip KumarGaur,Abhay KumarJha, (2016) Heat and Mass Transfer in Visco-Elastic Fluid through Rotating Porous Channel with Hall Effect. Open Journal of Fluid Dynamics,06,11-29. doi: 10.4236/ojfd.2016.61002

References

Appendix

, ,

,

,

Nomenclature

Dimensional concentration

x-component of current density

Concentration at the left plate

Mean absorption coefficient

Specific heat at constant pressure

Chemical reaction rate constant

Specific heat at constant pressure

Hall parameter

Distance of the plate

Hartmann number

Chemical molecular diffusivity

Nusselt number

Electric charge

Number density of the electron

Acceleration due to gravity

Dimensional pressure

Modified Grashof number for mass transfer

Electron pressure

Modified Grashof number for heat transfer

Prandtl number

Magnetic field

Radiative heat flux

Magnetic field of uniform strength

Dimensional heat source

x-Component of magnetic field

Heat source parameter

Current density

Radition parameter

Amplitude for steady flow

Temperature at the right wall

Resultant velocity

Dimensional time

Amplitude for unsteady flow

Schmidt number

Non zero constant mean velocity

Sherwood number

Dimensional temperature

Electron velocity

Temperature at the left wall

Visco-elastic parameter

Dimensional injection /suction velocity

Primary velocity component for unsteady flow

Primary velocity component for steady flow

Secondary velocity component for steady flow

Secondary velocity component for unsteady flow

Velocity components are in the directions respectively.

Greek Symbols

Phase difference for steady flow

Injection/suction parameter

Phase difference for unsteady flow

Dynamic viscosity

Phase difference for the flow

Magnetic permeability

Phase difference of mass flux

Kinematic viscosity

Small positive constant

Oscillation parameter

Dimensionless distance

Dimensional parameter

Phase difference of heat flux

Angular velocity

Fluid thermal conductivity

Cyclotron frequency

Electric conductivity

Amplitude of mass flux

Stefan-Boltzmann constant

Amplitude of heat flux

Non dimensional concentration

Density

Non-dimensional temperature

Coefficient of thermal expansion

Coefficient of thermal expansion

Coefficient of solutal expansion

Phase difference of shear stresses for the steady flow

Phase difference of shear stresses for the unsteady flow

Phase difference of shear stresses for the flow

Amplitude of shear stresses for the flow

Amplitude of shear stresses for the steady flow

Amplitude of shear stresses for the unsteady flow