Received 21 March 2015; accepted 30 May 2015; published 2 June 2015

ABSTRACT

The dynamics of unsteady magnetohydrodynamic convective fluid flow with radiation and thermophoresis of particles past a vertical porous plate moving through a binary mixture in an optically thin environment is investigated. The approximate form of the radiative heat flux is considered as the fourth power of temperature. Chemical reaction that occurs as the chemically reacting fluid flow through binary mixture is accounted for in energy and species concentration equations. Exponential space dependent heat source is introduced to generate additional heat energy across the fluid domain. The corresponding influence of heat energy is properly accounted for. It is assumed that viscosity and thermal conductivity vary as a linear function of temperature. The governing boundary layer equations are converted to nonlinear ordinary differential equations using similarity variables. A novel method of obtaining root finding starting with three guesses in shooting techniques is presented. The corresponding nonlinear coupled ordinary differential equations is solved numerically by shooting technique along with quadratic interpolation scheme. Graphical results of the dimensionless velocity, temperature and concentration distributions are shown for certain pertinent parameters controlling the fluid flow. The quadratic interpolation method is found to produce better estimated values of, , which satisfy the degree of accuracy and proportional to the physical quantities.

Keywords:

Variable Viscosity, Variable Thermal Conductivity, Binary Mixture, Quadratic Interpolation, Unsteady Flow, Thermophoresis, Exponential Heat Source, Shooting Technique

1. Introduction

In August 1904, Ludwig Prandtl presented a comprehensive report on aerodynamic boundary layer at International Congress of Mathematicians, Heidelberg, Germany. Since then, the study of thin layer formed on a vertical surface as fluid flows over a surface has received great attention because of its application in industry and engineering processes. Boundary layer flow past a surface moving through binary mixture is of important type of flow occurring in a number of engineering processes (i.e. chemical and petroleum). In industry, a familiar example of a binary mixture of fluids is an emulsion. Typical example of emulsion is oil dispersed within water or water within oil. A familiar example shows up when mixture of oil and water after shaken together is subjected to flow along a vertical heated surface due to buoyancy and pressure gradient. An emulsion is a dispersion (droplets) of one liquid in another immiscible liquid. Extensive reviews of this theory and its application can be found in Al-Sharif et al. [1] and Wang et al. [2] . By means of this model, Makinde et al. [3] carried out a research on unsteady convection with chemical reaction and radiative heat transfer past a flat porous plate moving through a binary mixture using the classical Boussinesq approximation. They assumed constant fluid viscosity within the boundary layer formed on vertical surface. The effects of increasing magnitude of suction/injection, wall temperature, Damkohler number and radiation parameter over velocity, temperature and concentration profiles are reported extensively. Their idea was then followed and extended by Makinde and Olanrewaju [4] ; hence, they introduced thermo-diffusion (Soret), Diffuso-thermal (Dufour) effects and reported the corresponding effects while Sastry and Murti [5] followed another direction by assuming that the fluid in question is electrically conducting and reported the effect of magnetic field parameter.

According to Somasundaran [6] , thermophoresis in liquid mixtures was first observed and reported by Carl Ludwig in 1856 and that of gas mixtures was first observed and reported by John Tyndall in 1870. Thermophoresis has many applications most especially as a method used to separate different polymer particles in field flow fractionation as reported by Giddings et al. [7] . The term thermophoresis often applies to aerosol mixtures but may also refer to the phenomenon in all phases of matter like liquid and gas (fluid). This phenomenon can be observed in mixtures of mobile particles where different particles exhibit different responses to the force of temperature gradient. A common example of thermophoresis is the blackening of the glass globe of a kerosene lantern; the temperature gradient established between the flame and the globe drives the carbon particles produced in the combustion process towards the globe where they deposit [8] . This contribution to the body of knowledge attracted Chamkha and Isaa [9] to study effects of heat generation/absorption and thermophoresis on hydromagnetic flow with heat and mass transfer over a flat surface. Animasaun [10] presented the effects of thermophoretic parameter on non-darcian MHD dissipative Casson fluid flow along linearly stretching vertical surface with migration of colloidal particles in response to macroscopic temperature. Recently, Fagbade et al. [11] employed SHAM to solve dimensionless governing equations which corresponds to a problem of Darcy- Forcheimer mixed convection flow in the presence of magnetic field and thermophoresis. Extensive studies on dynamics of MHD fluid flow past continuously moving semi-infinite surface with large suction, classical heat generation; radiation effects on MHD flow, unsteady MHD convection flow of polar fluids and effects of space and temperature internal heat source can be found in [12] -[19] .

Numerical solutions are of particular interest due to the fact that exact solutions do not exist in closed form for most engineering and scientific problems. A commonly used numerical method for the solution of two point boundary value problems is the shooting method. Shooting method is a classical and special methodology for solving boundary value problems of differential equations. Numerous strong nonlinear boundary-value ordinary differential equations arise in engineering and science. Shooting method has been adopted to solve several kinds of B.V.P. in published articles. The basic idea behind the proposed numerical method can be introduced as theoretical approach to solve System of Ordinary Differential Equations (Boundary Value Problem) based on conversion of B.V.P. to I.V.P. by using method of superposition introduced by Na [20] ; to obtain better estimate of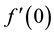, and 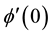which satisfy the boundary conditions at infinity by starting with three guesses, and finally to solve the I.V.P. using the initial conditions together with the better estimate. Through literature review, it is noticed that in all the studies on chemically reacting fluid flow past a surface moving through binary mixture, thermo-physical properties of the fluid are treated as constant function of temperature. However, it is known that these properties may change with temperature, most especially when Engineer introduces heat energy to enhance the transport phenomena. To accurately predict the dynamics of the flow and heat transfer rates, it is necessary to account for the variation in viscosity and thermal conductivity. This present paper is an extension of [3] -[5] by considering the Arrhenius kinetics, thermophoresis and thermal radiation in an unsteady MHD convective flow with temperature dependent viscosity and thermal conductivity over a moving plate through a binary mixture with suction at the plate surface. The governing equations are converted to ordinary differential equations by applying the similarity transformation. Numerical solutions of the reduced nonlinear similarity equations are then obtained by adopting Runge-Kutta Gill scheme along with the shooting method and the quadratic interpolation. The results of the numerical solution are then presented graphically for difference values of the various parameters.

2. Governing Equations of the Flow

An unsteady one-dimensional hydrodynamic convective flow of a viscous incompressible, electrically conducting and chemically reacting fluid flow past a porous vertical heated surface moving through a binary mixture is considered. The flow is assumed to be in the x-direction, which is taken along the semi-infinite plate and y-axis is normal to it. Since the surface is of infinite length in x-direction, therefore all the physical quantities (i.e. velocity, temperature and species concentration) are assumed to be independent of x. A uniform magnetic field 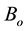is applied in the direction perpendicular to the surface. The fluid is assumed to be slightly conducting, and the magnetic Reynolds number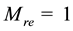; hence, the induced magnetic field is negligible in comparison with the applied magnetic field. It is further assumed that there is no applied voltage, so that electric field is absent. The fluid is assumed to be optically thin with absorption coefficient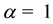. Following Cheng [21] , the approximate form of the radiative heat flux equation 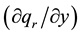is taken as the fourth power of temperature in the energy balance equation. It is assumed that heat and mass is transferred by free convection in the boundary layer over a vertical flat plate of constant temperature (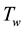) and concentration () which is embedded in a fluid-saturated porous medium of ambient temperature (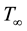) and concentration (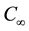) where and 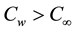respectively. This formulation is based on the notion that just as temperature gradient constitutes the driving potential for heat transfer, species concentration gradient in a mixture provides the driving potential for mass transfer [22] . The effect of thermophoresis is usually prescribed by means of the average velocity, which a particle will acquire when exposed to a temperature gradient [10] [23] . In boundary layer flow, the temperature gradient in the horizontal y-direction is very much larger than in the vertical x-direction, and therefore only the thermophoretic velocity in y-direction is considered [3] . In view of this, the component of thermophoretic velocity along the plate is negligible compared to the component of its velocity normal to the surface. Considering the mathematical model introduced by [4] [5] which is an extension of [3] together with all assumptions stated above along with classical Boussinesq’s approximation; the governing equations for continuity, momentum, energy, and species diffusion in laminar incompressible boundary layer flow can be written as follows:

(1)

(2)

(3)

(4)

Equations (1)-(4) are subject to boundary conditions

(5)

(6)

(7)

where is the plate characteristic velocity. From the continuity Equation (1), it is worth noticing that velocity component (v) is either constant or a function of time. Following [24] , velocity component along y-axis is considered as

(8)

where and are known as suction and injection respectively. In the energy Equation (3), the relationship between the activation energy and the rate at which a reaction proceeds is accounted for by using

(9)

In Equations (3), (4) and (9), it is very important to state that the frequency factor for the chemical reaction is. In this present study, it is worth mentioning that exponential space dependent internal heat source is introduced to increase the temperature of the fluid and to positively influence buoyancy. This concept can be traced to the idea of Crepeau and Clarksean [25] , El-Aziz and Salem [26] [27] and Animasaun et al. [28] . The increase of temperature may also leads to a local increase in the transport phenomena by reducing the viscosity across the momentum boundary layer and so the heat transfer rate at the wall may also be affected greatly. In [3] -[5] , fluid viscosity and thermal conductivity have been assumed to be constant function of temperature within the boundary layer. However, it is known that physical properties of the fluid may change significantly when expose to space dependent internal generated temperature or thermal stratification [29] . For lubricating fluids, heat generated by the internal friction and the corresponding rise in temperature affect the viscosity of the fluid and so the fluid viscosity can no longer be assumed constant. In order to account for the variation in thermo-physical properties of the fluid as it flows past a vertical heated surface moving through a binary mixture; classical Boussinesq’s approximation is adopted such that temperature of the wall/surface is greater than temperature of the fluid at free stream. In order to invoke this assumption, it is valid to consider the mathematical model of temperature dependent viscosity model used in [31] [32] which was developed using the experimental data of Batchlor [30] together with the mathematical model of temperature dependent thermal conductivity model of Charraudeau [33] as

(9)

where and are the constant value of the coefficient of viscosity and thermal conductivity at the free stream respectively. A case where is considered in this work and. The thermophoretic velocity parameter in Equation (4) was given in [8] and later by Tsai [34] as

(10)

is the thermophoretic coefficient which ranges in values from, 0.2 to 1.2 as indicated by Batchelor and Shen [35] and properly defined using the theory [8] as,

(11)

are constants, is the thermal conductivity of the fluids, is the thermal conductivity of the diffused particles, is the Cunningham correction factor, is the Knudsen number. Substituting all into dimensional governing Equations (1)-(4) we have

(12)

(13)

(14)

Considering the following dimensionless variables

(15)

Using (15), the following dimensionless non-linear ordinary differential equations are obtain

(16)

(17)

(18)

The dimensionless boundary conditions of the above problem are

(19)

(20)

where is Damköhler number, is the radiation parameter, is the activation energy parameter, is the modified thermal Grashof number, is the modified solutal Grashof number, is the heat source parameter, is the chemical reaction rate, is the Prandtl number, is known as Schmidt number, is known as thermophoretic parameter and M is the magnetic field parameter. Also, other quantities of physical interest in this problem are the local skin friction, local Nusselt number and Sherwood numbers which are defined by Makinde [3] as

(21)

And from that we can easily compute the results of the local skin friction, local Nusselt number and local Sherwood number.

3. Numerical Procedure

Following process for the step-by-step integration of differential equations in Gill [36] , the MATLAB Code (m-file) for solving system of O.D.E. using Runge-Kutta Gill can be found under Appendix I. In this code, denotes, and. The initial guess values are a, b and c. Runge Kutta Gill is also a fourth order Runge Kutta method with Local truncation error of and global truncation error. Delin and Zheng [37] , formulated a general formula of fourth Order Runge Kutta Method. Using a Lemma, they obtained the general method which is dependent on a parameter “t”. Five different fourth order Runge Kutta was obtained using the formula with t = 2 (the general scheme yielded classical Runge Kutta), t = 4 (the general scheme yielded England Runge Kutta Method) and when t = 1, 3 and 5 three other fourth Order Runge Kutta methods was also obtained. It was reported that numerical calculations using all these formulas have almost the same accuracy as the classical RK4. When we used, Runge Kutta Gill was obtained. There are two types of error involved in a Runge Kutta as an approximation method of Ordinary differential equations. They are Round off error and Truncation error. Runge-Kutta Gill method is selected because it reduces (minimize) round off error and this numerical scheme is one of the most widely used fourth order methods because it reduces the amount of storage required in the solution of a large number of simultaneous first order differential equations. According to Finlayson [38] , Order analysis, Consistency analysis and Stability analysis shows that Runge Kutta Gill is also of order four, stable and consistent. Considering system of second order ordinary differential equations (boundary value problem) as in (16)-(20), shooting method can be explained as follows. Let

(22)

represent the boundary value problem. Let, and denote the solution of the corresponding initial value problem after using method of superposition to reduce B.V.P. to I.V.P. as

(23)

Next step is to find a, b, c which must satisfy tolerance and conditions at infinity, and. We may define the function, and as

(24)

If in Equation (24) has a root “a”; certainly, the solution of the corresponding I.V.P. is also a solution of the B.V.P. in Equation (22). Also applicable to and. In addition, if the boundary value problem in Equation (22) has a solution, and, then, and are also the unique solution, and of the initial value problem where

(25)

Thus, “a” is a root of F₁, “b” is a root of F₂ and “c” is a root of F₃. In this study, the m-file (“Animasaun OJFD”) that contains the system of first order can be found under Appendix II. In the code, , , , , and. Using shooting method to solve nonlinear ordinary differential equation(s), zero finding problem for the function (Root finding) is a critical problem. It is very important to state that the two m-files must be in the same directory (folder) and patched to the command window of MATLAB. This problem is related to how to improve the solution (i.e. to get better estimate(s) of a, b and c that satisfy the B.V.P. and also meet up to our desirable degree of accuracy when compare to the condition(s) at infinity). Most researchers prefer to use Newton’s method, or Secant method namely linear interpolation. In this research, quadratic interpolation which resembles Muller’s method is adopted. This new approach is based on locally approximating the nonlinear function by a quadratic function and the root of the quadratic function is taken as an improved approximation to the root of the nonlinear function. The procedure is applied repetitively to convergence. Animasaun [39] stated that three initial approximations W, X, and Y which may or may not bracket the root are required to start the algorithm (see Table 1). The only difference between this new approach and the Secant method is that is a quadratic function while is a linear function in the Secant method. General procedure for fitting a polynomial to a set of equally spaced or unequally spaced data. The nth polynomial is

(22)

When, we shall obtain linear polynomial of the form

When, we shall obtain Quadratic Polynomial of the form

(23)

Using, when is guessed, set

When is guessed, set

Lastly, when is guessed, set

Solving for a₀, a₁ and a₂ simultaneously and then substitute into (23) to obtain

Finally leads to

(24)

The procedure is continued till the result of at N satisfy the desired degree of accuracy. Details can be found in [39] . It is worth mentioning that the convergence rate of the new approach of finding roots while shooting is faster than the rate of the secant method. Generally speaking, the secant method is specified because of its simplicity, even though its convergence rate is slightly smaller than the convergence rate of the new designed method which can be called Muller. The BVP cannot be solved on an infinite interval, and it would be impractical to solve it on a very large finite interval. In this research, the author imposed the infinite boundary conditions at a finite point of. To integrate the corresponding IVP, , and are require but no such values exist after the non-dimensionalization of the boundary conditions (19) and (20). The suitable guess values for, and are chosen and integration is carried out using the command under Appendix III. The calculated values for, and are compared with that of boundary condition (20). Adjustment of, and were carried out for better approximation for the solution of Equation (24). Care has been taken to shoot in steps; shoots are improved in stages and round off error is avoided by computing with 15 decimal places. Values of, and together with conditions in (19) are solved using Runge Kutta Gill

method with h = 0.01. To improve the solutions, quadratic interpolation (Muller’s method) is adopted. The above procedure is repeated until we get the results up to the desired degree of accuracy 10⁻⁵. The numerical solution described above is first written in 27 steps of Algorithm and implemented in a MATLAB environment together with Microsoft Excel software for proper analysis and extraction of data.

4. Results and Discussion

Numerical computations are carried out for the present problem by employing the similarity solution for, and against with variations of parameters controlling the fluid dynamics in the flow regime. The values of Schmidt number for hydrogen at 25˚C and one atmospheric pressure is considered in the analysis of the solution. It should be mentioned here that indicates an increase in the destructive chemical reaction rate, while corresponds to an increase in generative chemical reaction rate. The value of the Prandtl number is chosen to be, which represents air at 25˚C and one atmospheric pressure. When modified local thermal Grashof number this corresponds to cooling of the surface and when this corresponds to heating of the surface. In addition, when modified local solutal Grashof number this indicates that the chemical species concentration in the free stream region is less than the concentration at the surface/wall and when this indicates that the chemical species concentration in the free stream region is greater than the concentration at the surface/wall. From Table 2, it is observed that the convergence rate of linear interpolation (secant method) is slightly smaller than the convergence rate of the new technique (quadratic interpolation) method which can be referred to as Muller. This result is in good agreement with a related result in Hoffman [40] . According to the result, both linear interpolation (Secant Method) and quadratic interpolation (Muller’s method) are adopted to solve nonlinear problem (Four-bar linkage problem), it was reported that the convergence rate of Muller’s method is 1.84, which is faster than the 1.62 rate of the secant method and slower than the 2.0 rate of Newton’s method. Generally speaking, the secant method is preferred because of its simplicity even though its convergence rate is 1.62. In order to check the computational method for numerical accuracy, the author compares a special case of this present study with the numerical data published in Table 8 of Sastry and Murti [5] . As shown in Table 2 below, the results obtained are in good agreement. It is important to remark that due to the kind of fluid under consideration, using, the state of the fluid can not be changed from liquid to gas.

Figure 1 illustrates the influence of temperature dependent variable fluid viscosity and thermal conductivity on the fluid as it flows vertically upward past a moving surface through binary mixture in the presence of space dependent heat source. When modified buoyancy parameters, it is observed that as (ξ and λ) increases, the velocity asymptotically decreases near the vertical wall to a point near free stream and satisfies boundary condition. It is also seen that the velocity profile when greatly over shoot downward and tends to have negative values of velocity within. This result implies that, at a constant value of (b and δ) and, increase in (and) generates heat energy which can never subdue

corresponding influence of cooling of the fluid at the surface. This account for a drastic increase in the viscosity of the fluid as it flows (see Figure 1(a)). It is worth mentioning that at a constant value of space heat source parameters (,), as (ξ and λ) increases, the corresponding increase in heat energy tends to increase the temperature within the fluid domain. This account for the increase in temperature in the fluid domain as it flows (see Figure 1(b)). This also account for the decrease in the local skin friction coefficient as magnitude of (ξ and λ) increases (see Figure 4). In order to further unravel the dynamic of fluid as it flows past a moving surface through binary mixture when variable thermo-physical properties is considered, a case where is investigated.

It is observed that as (ξ and λ) increases, the velocity profiles decreases near the vertical wall and increases significantly thereafter as (see Figure 2(a)). This result is true since the rate of cooling of the surface has been reduced. This result also account for negligible increase of local skin friction coefficient with an increase in (ξ and λ) (see Figure 4). It is further observed that the temperature profiles increases with an increase in (ξ and λ). As the fluid rises along the vertical surface, it becomes cooled by the surface in the process. Due to this, influence of increasing (ξ and λ) is subdued near the wall. Few distances away from the wall, influence of increasing variable thermo-physical parameters (i.e. temperature dependent viscosity and thermal conductivity) enhances the transport phenomena. The variations of known as velocity profiles along with different values of (ξ and λ) are plotted in Figure 3 when. It is seen that the increase of both (ξ and λ) leads to significant increase of velocity profiles at all points within. When the fluid heats up, it’s molecules become excited and begin to move. The energy of this movement is enough to overcome the forces that bind the molecules together, allowing the fluid to move faster and decreasing its viscosity; hence, the velocity increases significantly from the wall to a point near the free stream with an increase in the magnitude of (ξ and λ). This account for the reason why local skin friction coefficient is an increasing function of (ξ and λ) as shown in Figure 4.

Figure 5(a) represents the velocity profiles for different values of magnetic field parameter (M). It is observed that velocity profile is a decreasing function of M. The magnetic field parameter represents the importance of magnetic field on the fluid as it flows vertically upward past a surface moving through binary mixture. The presence of transverse magnetic field sets in Lorentz force, which results in retarding force on the velocity field and therefore as magnetic field parameter increases, so does the retarding force. This account for the decrease in the velocity profiles. When variable thermo-physical properties are properly accounted for (i.e.), it is observed that which is related to skin friction coefficient decreases with magnetic field parameter (M) and increases with buoyancy parameters (G_r and G_c) (see Figure 5(b)). Figure 6(a) depicts the velocity profiles for different values of suction parameter. It is observed that the momentum boundary layer thickness and velocity distribution decreases with increase in suction (c > 0). This is in agreement with the usual fact that suction stabilize the boundary layer growth, as reported by (Makinde and Olanrewaju [4] ; Alam and Rahman [41] ). Wall suction removes the low-momentum fluid and delays both transition and separation. The effect of suction

parameter on the fluid temperature is highlighted in Figure 6(b). It is observed that the fluid temperature decreases near the wall and increases negligibly far from the wall. As the flow develops along a vertical surface moving through binary mixture, one way of dealing with boundary layer transition (flow separation) is to suck the thin boundary layer through the vertical porous surface. As this method reduces drag, heat energy escaped away from the flow regime; hence the temperature reduces as magnitude of suction increases.

As we all know in thermal science that heat energy migrates from region of high temperature to region of low temperature, this account for the reason why temperature profiles over shoot downward towards the region of low heat energy within the fluid domain as shown in Figure 6(b). The effect of suction parameter on the chemical species concentration in the boundary is depicted in Figure 7(a). From this figure, it is seen that the species concentration within the boundary layer decreases with an increase in the magnitude of c. Figure 7(b) displays the effect of τ over concentration profile when, ,; it is observed that solutal boundary layer decreases with an increasing values of parameter . This can be interpreted as follows; when all the small particles are suspended in the fluid domain and temperature gradient exists, all the particles experienced a force which pushes the particles towards the free stream (area of low heat energy). In particular, the effect of increasing the thermophoretic parameter τ is limited to decreasing the concentration profiles. This is true only for small values of Schmidt number for which the Brownian diffusion effect is large compared to the convection effect. The thermophoretic parameter is expected to alter the concentration boundary layer significantly. The effect of increasing τ in this research where, is in good agreement with that of [31] where, in which concentration profiles decreases with an increase in thermophoretic parameter.

5. Concluding Remarks

In this paper, effects of thermo-physical properties on unsteady convective flow with thermophoresis of particles, chemical reaction and radiative heat transfer past a porous vertical plate moving through a binary mixture are investigated. Quadratic interpolation technique is introduced with the fourth order Runge-Kutta Gill scheme to form shooting method. The following conclusions can be drawn as a result of the computation and analysis:

1) Velocity increases with increasing value of ξ when; velocity decreases with increasing values of ξ when. The two effects exist when.

2) Within the boundary layer of the problem considered, the effect of increasing suction (c > 0) leads to decrease of velocity, temperature (near the wall only) and concentration profiles.

3) Increase in thermophoretic parameter (τ) leads to significant decrease in concentration profiles.

4) Local skin friction coefficient is a decreasing function of magnetic field parameter at all values of buoyancy parameter within. When variable thermo-physical properties are accounted for in transport phenomena of fluid flow along a vertical surface moving through binary mixture in the presence of exponential heat source, Grashof number related to thermal and solutal is an important yard stick to control skin friction drag which arises from the friction of the fluid against the skin of the vertical surface that is moving through binary mixture. The convergence rate of the new approach (Quadratic Interpolation) of finding roots while shooting is faster than the rate of the secant method (Linear Interpolation).

References

Appendix I

function [eta,y] = Rungekgill(t0,tf,y0,f,n)

m = sqrt(2);

h = ( )/n; % In this study, t0 = 0 and tf = 3

t = linspace(t0,tf,n+1); % To discretize the independent variable “η”

y(1,:) = y0; % y0 is known as initial conditions in column vector

for i = 1: n; % here n = 300, implies that stepsize h = 0.01

k1 = h*feval(f,t(i),y(i,:));

k2 = h*feval(f,t(i)+(h/2),y(i,:)+(k1/2));

k3 = h*feval(f,t(i)+(h/2),y(i,:)+(m-1)*(k1/2)+(m-1)*(k2/m));

k4 = h*feval(f,t(i)+h,y(i,:)-(k2/m)+(m+1)*k3/m);

y(i+1,:) = y(i,:)+(k1)/6+((k2)*(2-m))/6+((k3)*(2+m))/6+(k4)/6;

end

Appendix II

function dy = AnimasaunOJFD(eta,y)

xi = 2; lamda = 2; c = 2.5; Gr = 1; Gc = 1; Da = 0.1; omega = 0.1; thetaw = 2; phiw = 2;

Ra = 0.5; M = 1; Pr = 0.71; Sc = 0.22; tau = 4; h = 1; n = 1; chi = 0.5; g = 1;

dy(1) = y(2);

dy(2) = ((xi/thetaw)*y(4)*y(2)-2*(eta+c)*y(2)-Gr*(xi/thetaw)*(y(3)-1)-Gc*(xi/phiw)*(y(5)-1)+M*y(1))/

(1+ xi - (y(3)*xi)/thetaw);

dy(3) = y(4);

dy(4) =(-(lamda/thetaw)*y(4)*y(4) - 2*Pr*(eta+c)*y(4) - (exp(omega - (omega/y(3))))*Da*Pr*h*(y(5))^n +

Ra*Pr*y(3)*y(3)*y(3)*y(3)- 4*chi*(y(3)-1 )*exp(-g*eta))/(1+((lamda*y(3))/thetaw)-(lamda/thetaw)) ;

dy(5) = y(6);

dy(6) = - Sc*2* (eta+c)*y(6)+(exp(omega-(omega/y(3))))*Da*Sc*(y(5))^n+Sc*(tau/thetaw)*y(4)*y(6) +

Sc*(tau/thetaw)*(y(5)-1)*((-(lamda/thetaw)*y(4)*y(4)-2*Pr*(eta+c)*y(4)-(exp(omega-(omega/

y(3))))*Da*Pr*h*(y(5))^n+Ra*Pr*y(3)*y(3)*y(3)*y(3)- 4*chi*(y(3)-1 )*exp(-g*eta))/(1 +

((lamda*y(3))/thetaw)-(lamda/thetaw)));

Appendix III

Them-files “Rungekgill”and “AnimasaunOJFD” must be in the same folder, and then patch with MATLAB command window.Lastly, paste the command below on Command window.

>>[eta,y]=Rungekgill(0,3,[1;a;2;b;2;c],'AnimasaunOJFD',300) % Assign values for a, b and c.