Open Journal of Fluid Dynamics
Vol.04 No.03(2014), Article ID:49513,14 pages
10.4236/ojfd.2014.43020
Numerical Analysis of Turbulent Fluid Flow and Drag Coefficient for Optimizing the AUV Hull Design
João Victor Nunes de Sousa1*, Antônio Roberto Lins de Macêdo2, Wanderley Ferreira de Amorim Junior1, Antonio Gilson Barbosa de Lima1
1Department of Mechanical Engineering, Center of Sciences and Technology, Federal University of Campina Grande, Campina Grande, Brazil
2ARMTEC Technology in Robotics, Fortaleza, Brazil
Email: *joao.vns@hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 July 2014; revised 1 August 2014; accepted 1 September 2014
ABSTRACT
Autonomous Underwater Vehicles (AUVs) are robots able to perform tasks without human intervention (remote operators). Research and development of this class of vehicles has growing, due to the excellent characteristics of the AUVs to operate in different situations. Therefore, this study aims to analyze turbulent single fluid flow over different geometric configurations of an AUV hull, in order to obtain test geometry that generates lower drag force, which reduces the energy consumption of the vehicle, thereby increasing their autonomy during operation. In the numerical analysis was used ANSYS-CFX® 11.0 software, which is a powerful tool for solving problems involving fluid mechanics. Results of the velocity (vectors and streamlines), pressure distribution and drag coefficient are showed and analyzed. Optimum hull geometry was found. Lastly, a relationship between the geometric parameters analyzed and the drag coefficient was obtained.
Keywords:
AUV, Hull, Drag Coefficient, Numerical Simulation

1. Introduction
An Autonomous Underwater Vehicle, or AUV, is defined as a robot which travels underwater without physical communication with the land and without the necessity of the human operator. The AUVs are included in the group of Unmanned Underwater Vehicles, better known as UUVs.
During the last years, several AUVs have been developed and researches in the area are becoming more frequent, due to the extremely favorable characteristics that these robots have, like the ability to operate autonomously in hostile environments, such as unexplored areas, enemy water territories (in wartime), contaminated or deepwater areas, etc. All these features make the use of AUVs very interesting for military, scientific and industrial sectors.
Most existing AUVs use batteries as an energy source for the propulsion system. High value of drag force generated during the displacement of the robot increases the energy consumption of the system and therefore the AUV autonomy will be lowered, which is undesirable for any engineer.
Viscous fluid passing around axisymmetric body such a cylinder, sphere and spheroid has been reported in many studies [1] -[4] . The behavior of viscous fluid flow is described by Navier-Stokes Equations, which are particular forms of Newton’s Laws of Motion, supplemented by an equation describing the conservation of mass, subjected to the prevailing boundary conditions. Except for very simple conditions, these equations need to be solved numerically with the aid of computers. For solution, the previously defined continuous flow domain is converted in a discrete domain by a numerical mesh. The flow governing differential equations are then transformed, using numerical discretisation schemes, in sets of algebraic equations. The coupled algebraic equations are then solved, by using linear methods, on a computer to yield discrete values of velocity and pressure at mesh nodes. The collection of theoretical, numerical and computational techniques that facilitate this process is called Computational Fluid Dynamics (CFD). Within the area of CFD, some of the most challenging flows are turbulent. Particular interest in turbulence derives from the fact that it is largely responsible for dispersion, mixing, vibrations, frictional losses and noise. Being a highly effective mechanism for momentum redistribution, turbulence has a major impact on hydrodynamic characteristics [5] -[8] .
Many authors uses CFD in submersible vehicle projects and optimizations due to the large amount of information obtained with reduced cost and time compared with experimental tests. Barros et al. [9] compared the analytical and semi-empirical results with numerical results for normal force and momentum coefficient of an AUV. It was shown that the CFD approach allows for a good prediction of the coefficients and shows qualitative information from flow visualizations; Juong et al. [10] used CFD to optimize the design of an AUV hull. They used a commercial software and they obtained an optimum value of nozzle angle, drag force and pressure and velocity fields; Malik et al. [11] used CFD to calculate the hydrodynamic derivates for a submersible vehicle in transient flow regime. It was concluded that the CFD method is well capable of economically evaluating the hydrodynamic derivatives of submersible platforms such as submarines, torpedoes and autonomous underwater vehicles; Dantas et al. [12] used CFD to analyze the influence of control surfaces in manoeuvrability of an AUV. It was verified that the occurrence of the control surface stall depends on a linear relationship between the angle of attack and the control surface deflection.
Therefore this paper aims to predict fluid flow around the hull of an AUV. Here is created a numerical model analyzing some geometric configurations for the hull of an AUV, to obtain geometry that generates low drag and is suitable for application to this class of vehicles.
2. Methodology
2.1. The Geometry of Hull
The hull of AUV is torpedo type (cylindrical body with a large ratio between the length and the diameter), due to its good features, which explains the widespread use of this type of hull by all major manufacturers of AUVs.
To model the profiles of the bow and stern of the vehicle it was used the Myring Equations. These theoretical equations describe curves for bow and stern of the torpedo bodies which generate the smallest possible drag coefficient [13] . The equations are as follows:
・ Bow,
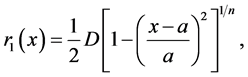 (1)
(1)
・ Stern,
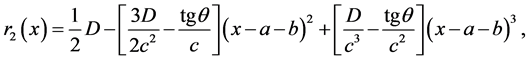 (2)
(2)
where all parameters of these equations, with the exception of the parameter n, are geometric, and are shown in Figure 1.
In this paper the geometric parameters considered are shown in Table 1. These parameters were based on dimensions of AUVs existing in the market.
The influence of the parameters n and θ in the drag of the hull was the focus of this paper. Profiles with n equal to 1, 2, 3 and 4, and θ equal to 15˚, 20˚, 25˚ and 30˚ were examined. The choice of these ranges of the bow and stern was based in previous works found in the literature [9] [10] [12] [14] and images of others torpedo bodies.
Figure 2 and Figure 3 show the profiles (with the altered scale for clarity) to bow and stern, respectively, which were used in the numerical simulation.
2.2. The Physical Domain and the Numerical Mesh
The dimensions of the fluid domain were obtained after various computational tests until to reach an optimal
Figure 1. Squematic figure of the AUV hull and geometric parameters of Myring Equations.
Table 1. AUV geometric parameters used in the simu- lations.
Figure 2. Bow profiles analyzed for different parameters n.
size of the field, allied to good results with good accuracy and low computational time. Figure 4 shows the dimensions of the domain as a function of the maximum diameter, D = 200 mm, and the total length of AUV, L = 1800 mm. It was opted for a semi-cylindrical domain, seeking a smaller number of control volumes, when compared to a quadrilateral domain, thus reducing the computational cost.
Figure 5 illustrates the mesh representing the study domain, which was built with the support of ICEM-CFD® 11.0 software. A mesh was made for each variation in curves of the bow and stern. These non-structured meshes were obtained after various refinements, and have approximately 550,000 tetrahedral elements.
Figure 6 shows details of the mesh, especially the region in front of the hull, the region of the boundary layer and wake region.
Much care must be taken when constructing numerical meshes aimed at solving problems of flow around immersed bodies. Here, many factors were taken into account [15] . It was used the Equation (3) that provides the average thickness of the kinetic boundary layer (region where viscous flow effects are important) around immersed bodies, δ, as follows:
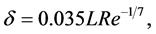 (3)
(3)
where Re is Reynolds number of the flow, calculated as follows:
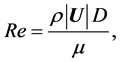 (4)
(4)
where ρ is the fluid density, 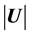 is the norm of flow velocity vector and μ is the fluid viscosity. The meshes were built with great refinement near the surface of the AUV (boundary layer region), in order to encompass precisely the viscous effects of the flow around the AUV.
is the norm of flow velocity vector and μ is the fluid viscosity. The meshes were built with great refinement near the surface of the AUV (boundary layer region), in order to encompass precisely the viscous effects of the flow around the AUV.
Figure 3. Stern profiles for different parameters θ.
Figure 4. Fluid domain.
Figure 5. Mesh created in the studied domain.
2.3. Mathematical Modeling
To investigate the single-phase flow of sea water around the hull of AUV, it was considered three-dimensional, permanent, incompressible and isothermal turbulent flow.
The general equations used in this work are:
・ Mass conservation equation,
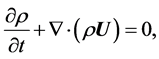 (5)
(5)
where 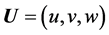 is the velocity vector,
is the velocity vector,
Figure 6. Details of the mesh: region in front of the hull (up), region of the boundary layer (center) and wake region (down).
・ Momentum conservation equation,
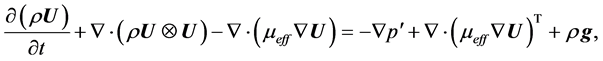 (6)
(6)
where 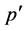 is the corrected pressure, which depends of turbulent model to be used,
is the corrected pressure, which depends of turbulent model to be used, 

where 
It is necessary to add in the model new equations governing the phenomenon of turbulence that is present in the flow. The turbulence consists of fluctuations in the flow field in time and space (time-dependent velocity and pressure fields). It is a complex process and can have a significant effect on the flow characteristics. Turbulence occurs when the inertial forces acting on the fluid becomes significantly higher than the viscous forces and is characterized by a high Reynolds Number of the flow. Turbulence can also be caused by surface roughness, which induces secondary flow (i.e. vortices) [16] .
The turbulence model adopted in this work is the Shear Stress Transport model (SST model), which is based on the turbulence k-ω model. This model was used because of its good treatment of external flow with high Reynolds numbers. It was considered flow fully turbulent around the AUV.
The SST model introduces two new variables in the problem, which are k, which is the turbulent kinetic energy, and ω, which is the turbulent frequency. These variables are calculated by:
・ Turbulent kinetic energy equation,

where Pk is the turbulence production, Ck1 = 2.000 and Ck2 = 0.009.
・ Turbulence frequency equation,

where Cω1 = 2.000, Cω2 = 0.556 and Cω3 = 0.075. In the SST model the parameters μt, p' and Pk are given as follows:



where pd is the dynamic pressure, calculated by the equation

Total pressure, pt, is calculated by:

where ps is the static pressure.
According to Warsi [6] the action of viscosity is diminish the velocity of fluid past a surface and, thus, decreasing the fluid momentum within the boundary layer. It strongly affects the overall flow behavior past the surface. Since, fluid flow is governed by the pressure distribution impressed on the boundary layer. We must analyze both the retarding action of viscosity and the imposed pressure distribution. Thus is done calculated the drag coefficient in the flow. The total drag force is generated by the friction and pressure forces acting on a body immersed in a flowing fluid.
The friction drag is due to the boundary layer surface shear stress, while pressure drag is due to pressure difference in the flow direction resulting from formation of the wake in the downstream region.
The drag on a body is usually expressed in terms of a dimensionless drag coefficient. The total drag coefficient, Cd, is calculated by:

where Cdf is the friction drag coefficient, Cdp is the pressure drag coefficient (form drag), Fdf is the friction drag force, Fdp is the pressure drag force, U* is the free stream fluid velocity and Af is the frontal area of AUV. Fdf and Fdp are calculated by:


where τ is the shear stress, A is the AUV superficial area and î is the unitary vector in parallel flow direction.
2.4. Boundary Conditions and Fluid Properties
Figure 7 shows domain with indicative information related to boundary conditions and Table 2 shows specified values of these boundary conditions.
The fluid adopted in all simulations was sea water with 35 g/L of salinity, on the depth of 1000 m (temperature of 15˚C and static pressure 10.2 MPa). The properties of the fluid are showed in Table 3. The flow analyzed has Re = 4.2 × 106.
Table 4 shows the considerations adopted for the numerical solver.
2.5. Validation of the Results
To validate the methodology for constructing the numerical mesh, as well as the mathematical model used in this
Figure 7. Physical specification of the domain with the boundary conditions.
Table 2. Boundary conditions used in the simulations.
a. No slip and smooth wall; b. Opening condition; c. Pressure on the depth of 1000 m.
Table 3. Fluid properties.
Table 4. Considerations adopted in numerical solver.
study, we analyzed the axial flow on two well-known geometries: a cylinder and ellipsoid of revolution (Figure 8). Was chose these cases because of the similarity of these geometries with the AUV hull.
The simulations for validation are subject to the same considerations, boundary conditions and mathematical model described in the previous sections.
The drag coefficient, Cd, as well as corresponding friction drag coefficient, Cdf, and pressure drag coefficient, Cdp, obtained numerically will be compared with those obtained experimentally.
The following is detailed for geometry was conducted to evaluate how the experimental coefficient of drag:
a) Cylinder: Length L = 1800 mm and diameter D = 200 mm. Reference [17] shows Cd, Cdf and Cdp, obtained experimentally for Re ≥ 104, as a function of ratio L/D. For L/D = 9, Cd ≈ 0.85, where approximately 90% is referent of Cdp;
b) Ellipsoid: Length of major axis L' = 1800 mm and length of minor axis L² = 200 mm. Reference [17] shows Cd (Equation (18)), Cdf and Cdp, obtained experimentally for Re ≥ 105, as a function of ratio L'/L''. For the analyzed case, Cd ≈ 0.117, where approximately 100% is referent of Cdf.

3. Results and Discussion
Table 5 and Table 6 show the comparison between the numerical and experimental results of different drag coefficients cited in the text for the cases of flow around cylinder and ellipsoid. The difference between the results is small, being of the order of 7.1% for the case of the cylinder and 12.0% for the ellipsoid. Moreover, there was also a good approximation between the corresponding pressure and friction drag fractions. The low deviations between the results validate the methodology used in this work, showing that it describe well the studied phenomenon.
Figures 9-12 illustrate, respectively, the velocity field around the cylinder (streamlines), the velocity vector field around the cylinder, the velocity field around the ellipsoid (streamlines) and the velocity vector field around the ellipsoid by vectors, in the longitudinal symmetry plane for the analyzed cases. Because the shape of cylinder is very different of ellipsoid, in the flow pattern more intense turbulence zones are found, specially in the wake zone. In cylinder case is visible more intense recirculation zones in the flow behind the cylinder (wake region), in comparison with the ellipsoid, thus, increasing Cdp factor. For this reason Cd for cylinder is dramatically higher than the ellipsoid.
For analyze the drag of AUV hull by varying the shape of the bow (Figure 13) was used stern profile with θ = 25˚.
Table 7 shows the complete comparison between the results of the drag coefficients obtained by varying the parameter n. Further, the average shear stress at the AUV surface, τave, and the difference of pressure between the point x = 0 and the point x = 1.8 m in longitudinal axis of AUV (Figure 1), Δp, are showed too.
It was found that with increasing the parameter n we have an increase in the total drag, Cd, and particularly in
Figure 8. Cylinder and ellipsoid of revolution used in the validation.
Table 5. Comparison between experimental and numerical results of the drag coe- fficients for flow around the cylinder.
a. Reference [17] .
Table 6. Comparison between experimental and numerical results of the drag coe- fficients for flow around the ellipsoid.
a. Reference [17] .
Figure 9. Streamline showing the velocity field around the cylinder, with emphasis for recirculation zones.
Figure 10. Vectors showing the velocity field in the recirculation zones around the cylinder.
Figure 11. Streamline showing the velocity field around the ellipsoid.
Figure 12. Vectors showing the velocity field in the small recirculation zone around the ellipsoid.


Figure 13. Bow profiles used in the simulations (θ = 25˚).
Table 7. Results for bow profiles (θ = 25˚).
the portion corresponding to the drag pressure, Cdp. However, it is seen that these parameters does not vary much over the range computed. In all cases, the predominant fraction of the drag is due to friction, Cdf, accounting for over 80% of total drag. It is verified that the increasing the parameter n the parameters τave increase and Δp oscillate. Based on data obtained was defined the profile with n = 2 as ideal shape for the bow. The profile with n = 2 is the most efficient because it gives to the hull a lower drag (only 0.9% above the drag of the hull profile when n = 1) and a good internal volume of the bow (25.0% above of the hull profile when n = 1), which would facilitate the accommodation of all internal systems of the vehicle.
With the bow profile with parameter n = 2 fixed, were simulated cases changing the parameter θ which alters the stern shape (Figure 14).
Table 8 shows the complete comparison between the results obtained for the drag AUV hull by varying the parameter θ. Figure 15 shows the results graphically.
It is found that the best performance profile is that when parameter θ = 20˚, giving to the hull the lowest drag coefficient, which is 2.5% less than the hull with the worst profile analyzed in this section, which is the profile with θ = 30˚. Is verified that the increasing the parameter θ the parameters τave increase and Δp decrease.
The ideal geometry among the analyzed cases is shown in Figure 15. The geometry has parameters n = 2 and θ = 20˚.
Based on the simulations results it was obtained a correlation between the parameters n and θ with Cd (Equation (19)). This equation were obtained by the method of the least squares, with determination coefficient of 0.99694, and valid for the ranges 1 ≤ n [-] ≤ 4 and 15 ≤ θ [degree] ≤ 30.

The optimal design gives the hull a drag coefficient of 0.1230, which is very close to the drag coefficient of the ellipsoid (just 5.1% upper), with the advantages of easier construction and approximately 10.3% more in volume.


Figure 14. Stern profiles used in the simulations (n = 2).
Table 8. Results for the stern profiles (n = 2).
Figure 15. Ideal AUV hull design, among the studied cases.
Figure 16 shows the total pressure field around the ideal AUV hull, in the longitudinal symmetry plane. It is verified the higher pressure in the stagnation point of the flow. Further, it is verified the high pressure values and low range. This is due the high contribution of static pressure, ps, in the total pressure, due the big depth (1000 m) in that the study was performed.
Figure 17 and Figure 18 show the velocity field around the ideal AUV hull. By analyzing these figures we can see the low velocity in the wake region and the null velocity in stagnation point. Is visualized yet the velocity profile in kinetic boundary layer in stern region.
4. Conclusion
In this paper the hydrodynamic single-phase flow around the AUV hull is discussed. The study is related to sea water flow in the turbulent regime by using the ANSYS-CFX® 11.0 commercial software. The simulations revealed the good mathematical treatment used, with good precision between numerical and experimental results. It reached an optimized design for AUV hull that has a drag coefficient of 0.1230, which is very close to the drag coefficient of the ellipsoid, with 10.3% more volume, and is about 7 times smaller than the cylinder, proving the efficiency of the use of bow and stern smoothed profiles.
Acknowledgements
The authors would like to express their thanks to Brazilian Research Agencies CNPq, CAPES and FINEP and ARMTEC Technology in Robotics for supporting this work, and are also grateful to the authors of the references
Figure 16. Total pressure field for ideal AUV hull (n = 2 and θ = 20˚).
Figure 17. Velocity field around the AUV, in terms of streamlines.
Figure 18. Velocity vector field around the AUV.
in this paper that helped in the improvement of quality
References
- Proudman, I. and Pearson, J.R.A. (1957) Expansions at Small Reynolds Numbers for the Flow Past a Sphere and a Circular Cylinder. Journal of Fluid Mechanics, 2, 237-262. http://dx.doi.org/10.1017/S0022112057000105
- Masliyah, J.H. and Epstein, N. (1970) Numerical Study of Steady Flow Past Spheroids. Journal of Fluid Mechanics, 44, 493-512. http://dx.doi.org/10.1017/S0022112070001957
- Masliyah, J.H. and Epstein, N. (1971) Steady Symmetric Flow Past Elliptical Cylinder. Industrial & Engineering Chemistry Fundaments, 10, 293-299. http://dx.doi.org/10.1021/i160038a017
- Rosenfeld, M., Wolfshtein, M. and Israeli, M. (1992) A Numerical Study of the Laminar Incompressible Flow Over a 6:1 Prolate Spheroid at 10˚ Incidence. International Journal for Numerical Methods in Fluids, 15, 147-173. http://dx.doi.org/10.1002/fld.1650150203
- White, F.M. (1991) Viscous Fluid Flow. 2nd Edition, McGraw-Hill, New York.
- Warsi, Z.U.A. (1999) Fluid Dynamics: Theoretical and Computational Approaches. 2nd Edition, CRC Press, Boca Raton.
- Ferziger, J.H. and Peric, M. (1999) Computational Methods for Fluid Dynamics. 2nd Edition, Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-98037-4
- Spurk, J.H. and Aksel, N. (2008) Fluid Mechanics. 2nd Edition, Springer-Verlag, Berlin.
- Barros, E.A., Dantas, J.L.D., Pascoal, A.M. and Sá, E. (2008) Investigation of Normal Force and Moment Coefficients for an AUV at Nonlinear Angle of Attack and Sideslip Range. IEEE Journal of Oceanic Engineering, 33, 538-549. http://dx.doi.org/10.1109/JOE.2008.2004761
- Juong, T., Sammut, K., He, F. and Lee, S.K. (2009) A Study on the Design Optimization of an AUV by Using Computational Fluid Dynamic Analysis. Proceedings of the 19th International Offshore and Polar Engineering Conference, Osaka, 21-26 June 2009, 696-702.
- Malik, S.A. and Guang, P. (2013) Transient Numerical Simulation for Hydrodynamic Derivates Predictions of an Axisymmetric Submersible Vehicle. Research Journal of Applied Sciences, Engineering and Technology, 5, 5003-5011.
- Dantas, J.L.D. and Barros, E.A. (2013) Numerical Analysis of Control Surface Effects on AUV Manoeuvrability. Applied Ocean Research, 42, 168-181. http://dx.doi.org/10.1016/j.apor.2013.06.002
- Myring, D.F. (1976) A Theoretical Study of Body Drag in Subcritical Axisymmetric Flow. The Aeronautical Quartely, 27, 186-194.
- Jun, B.H., Park, J.Y., Lee, F.Y., Lee, P.M., Lee, C.M., Kim, K., Lim, Y.K. and Oh, J.H. (2009) Development of the AUV “ISiMI” and a Free Running Test in an Ocean Engineering Basin. Ocean Engineering, 36, 2-14. http://dx.doi.org/10.1016/j.oceaneng.2008.07.009
- ANSYS (2006) ANSYS CFX-Solver Theory Guide (Release 11.0). ANSYS, Inc., Canonsburg.
- Kaviany, M. (2001) Principles of Convective Heat Transfer. 2nd Edition, Springer, New York. http://dx.doi.org/10.1007/978-1-4757-3488-1
- Hoerner, S.F. (1965) Fluid-Dynamic Drag. Published by the Author, New York.
NOTES
*Corresponding author.



















