Open Journal of Fluid Dynamics
Vol.3 No.4(2013), Article ID:40401,4 pages DOI:10.4236/ojfd.2013.34030
Mechanical Analysis of Viscous-Elastic Fluid Acting on Residual Oil in the Micro Pore
1Department of Petroleum Engineering, Northeast Petroleum University, Daqing, China
2Daqing Petroleum Equipment Group, Daqing, China
3Technical Development Department, The 2nd Oil Production Factory of Daqing Oilfield Company Limited, Daqing, China
Email: dqliull2009@163.com
Copyright © 2013 Lili Liu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 14, 2013; revised June 14, 2013; accepted June 22, 2013
Keywords: Viscous-Elastic Fluid; Residual Oil; Normal Deviatoric Stress; Micro Pore
ABSTRACT
In order to analyze the normal deviatoric stress that viscous-elastic fluid acting on the residual oil under the situation of different flooding conditions and different permeabilities, Viscous-elastic fluid flow equation is established in the micro pore by choosing the continuity equation, motion equation and the upper-convected Maxwell constitutive equation, the flow field is computed by using numerical analysis, the forces that driving fluid acting on the residual oil in micro pore are got, and the influence of flooding conditions, pore width and viscous-elasticity of driving fluid on force is compared and analyzed. The results show that: the more viscous-elasticity of driving fluid increases, the greater the normal deviatoric stress acting on the residual oil increases; using constant pressure gradient flooding, the lager the pore width is, the greater normal deviatoric stress acting on the residual oil will be.
1. Introduction
In the enhanced oil recovery, the viscous-elastic fluid flooding is a very important part. Many scholars have made a lot of efforts on viscous-elastic fluid enhancing oil recovery. By experimental studies Wang Demin [1] found that viscous-elastic polymer solution can improve flooding efficiency in micro pore; Yin Hongjun [2] studied that the rheology of viscous-elastic polymer solution in the dead end: Xia Huifen [3] discussed the microscopic mechanism of viscous-elastic polymer solution improving flooding efficiency. In the paper, the force of viscous-elastic fluid acting on residual oil is analyzed theoretically under different flooding conditions, different permeabilities, which lays the foundation for further analysis of deformation.
2. Calculation Model
In order to analyze the force acting on residual oil in micro pore of different width, a calculation model is established shown in Figure 1, Where H is the pore width, takes 20 μm, 40 μm, 60 μm respectively. The core is oil wet. The film height is 10 μm, the length is 40 μm.

Figure 1. Calculation model.
The boundary conditions are setted: The inlet and an outlet, respectively, use a constant velocity (1e - 5 m/s), constant flow rate (2e - 10 m3/s) and constant pressure gradient (0.02 MPa/m). The boundaries meet the no-slip condition and assume that the film is stationary.
3. Basic Equations
Viscous-elastic fluids have got complex rheological properties. Based on experiment research, the upper-convected Maxwell constitutive equation is suitable to describe the rheological properties of viscous-elastic fluid. The corresponding continuity equation, motion equation and constitutive equation [4] are:
Continuity equation:
 (1)
(1)
where: u is velocity vector.
Momentum equation:
 (2)
(2)
where: F is mass force; ρ is density; P is stress tensor.
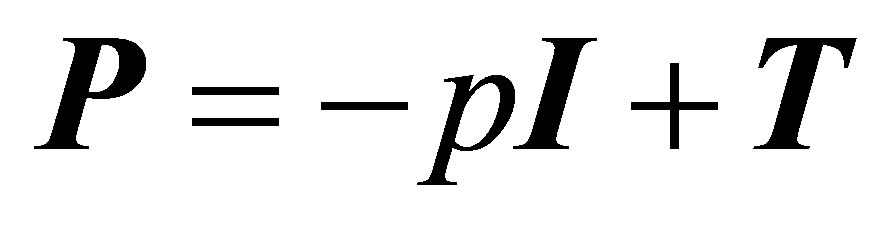 (3)
(3)
where I is unit tensor; −p is static pressure; T is deviatoric stress tensor.
Constitutive equation:
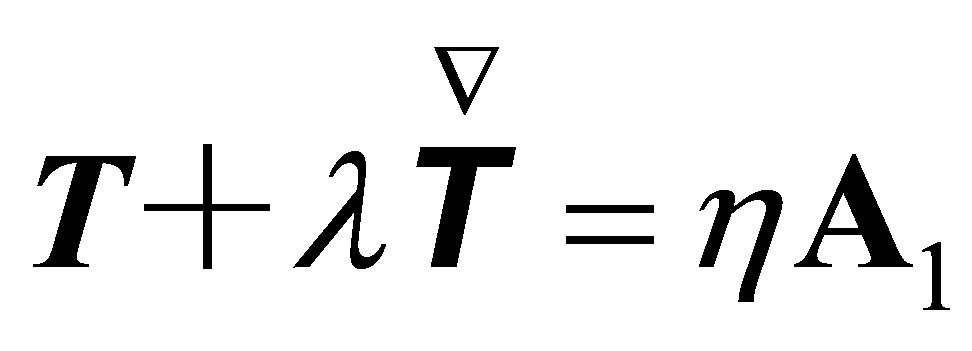 (4)
(4)
where: λ is relaxation time, which is the characterization of fluid elasticity; η is shearing viscosity; A1 is one order Rivlin-Ericksen tensor.
4. Calculation Results
The Weissenberger number is a dimensionless quantity which is used to describe fluid elasticity. The greater its value is, the stronger the fluid elasticity is. The formula is:
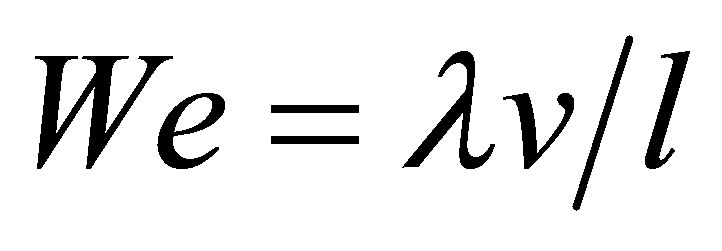
where We is the Weissenberger number; v is characteristic velocity; l is characteristic length.
4.1. The Change of Normal Deviatoric Stress Acting on Residual Oil under Different Flooding Conditions
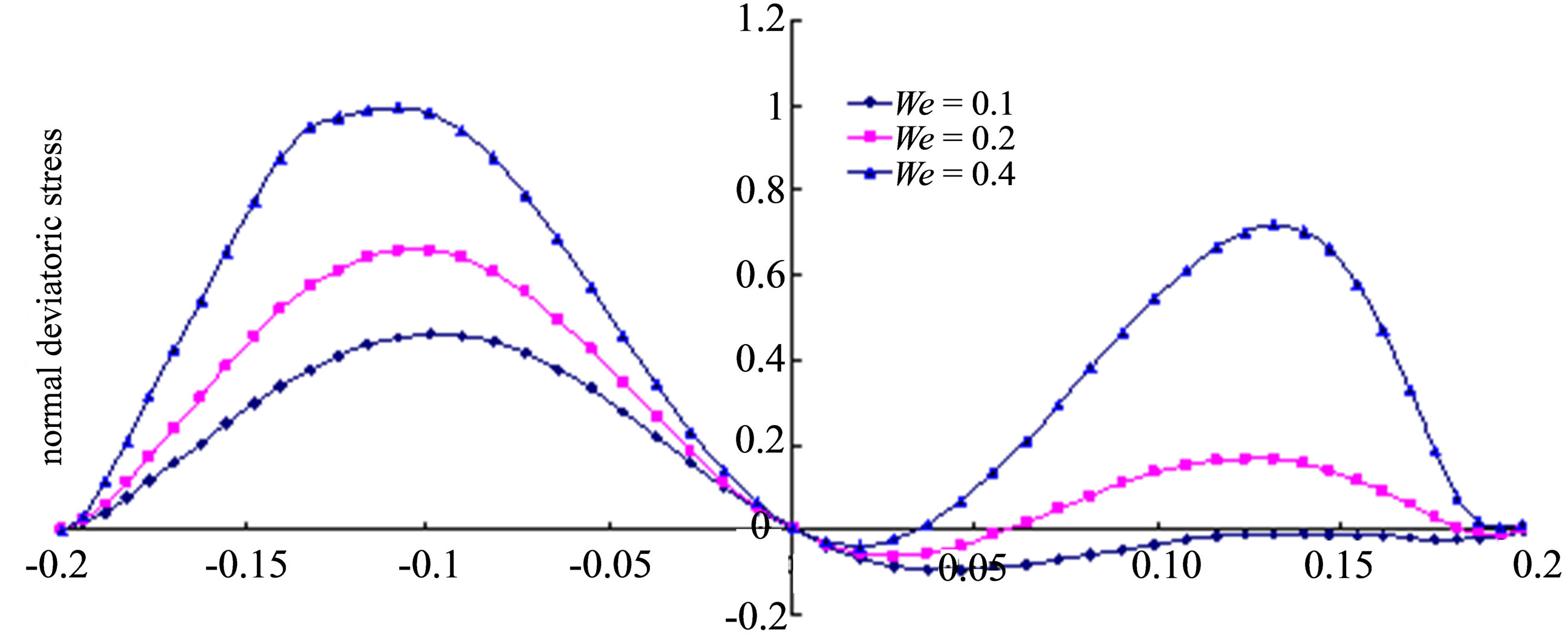
For the same pore width (20 μm, for example), using constant velocity (1e - 5 m/s), constant flow rate (2e - 10 m3/s) and constant pressure gradient (0.02 MPa/m), respectively. The normal deviatoric stress acting on the residue oil is calculated by different viscous-elastic fluid. As is shown in Figure 2, for the same pore width, the conditions of constant velocity and constant flow rate are the same.
 (a)
(a)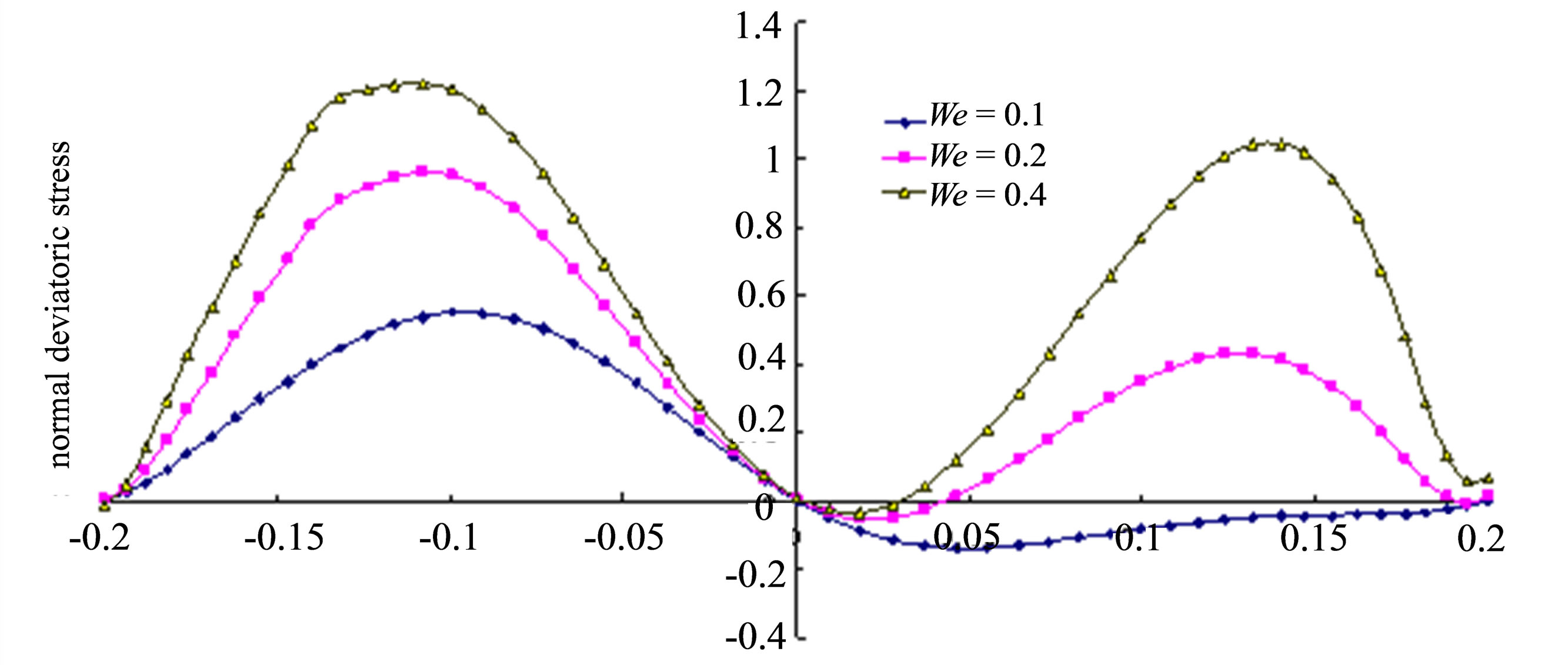 (b)
(b)
Figure 2. Normal deviatoric stress acting on the residue oil by viscous-elastic fluid of different We (pressure is positive, tension is negative); (a) Constant velocity (constant flow rate); (b) Constant pressure gradient.
It can be seen from Figure 2, no matter which of the conditions of constant velocity, constant flow rate or constant pressure gradient, the normal deviatoric stress increases as We increases. Which shows that the more viscous-elasticity of viscous-elastic fluid is, the more bigger normal deviatoric stress is.
4.2. The Change of the Normal Deviatoric Stress Acting on Residual Oil under Different Permeability Micro Pores
For the same We, micro pores of 20 μm 40 μm and 60 μm respectively, the forces acting on residual oil under the flooding conditions of constant velocity (1e - 5 m/s), constant flow rate(2e - 10 m3/s) and constant pressure gradient (0.02 MPa/m), are calculated, which is shown in Figure 3.
It can be seen from Figure 3, when flooding with constant pressure gradient, with the increase of the pore width, the normal deviatoric stress increases. On the contrary, when flooding with constant flow rate and constant velocity, the normal deviatoric stress reduces with the pore width increases. Flooding with pressure gradient in the oilfield, the high permeability zone supports more force, residual oil deforms greater relatively and is more
 (a)
(a)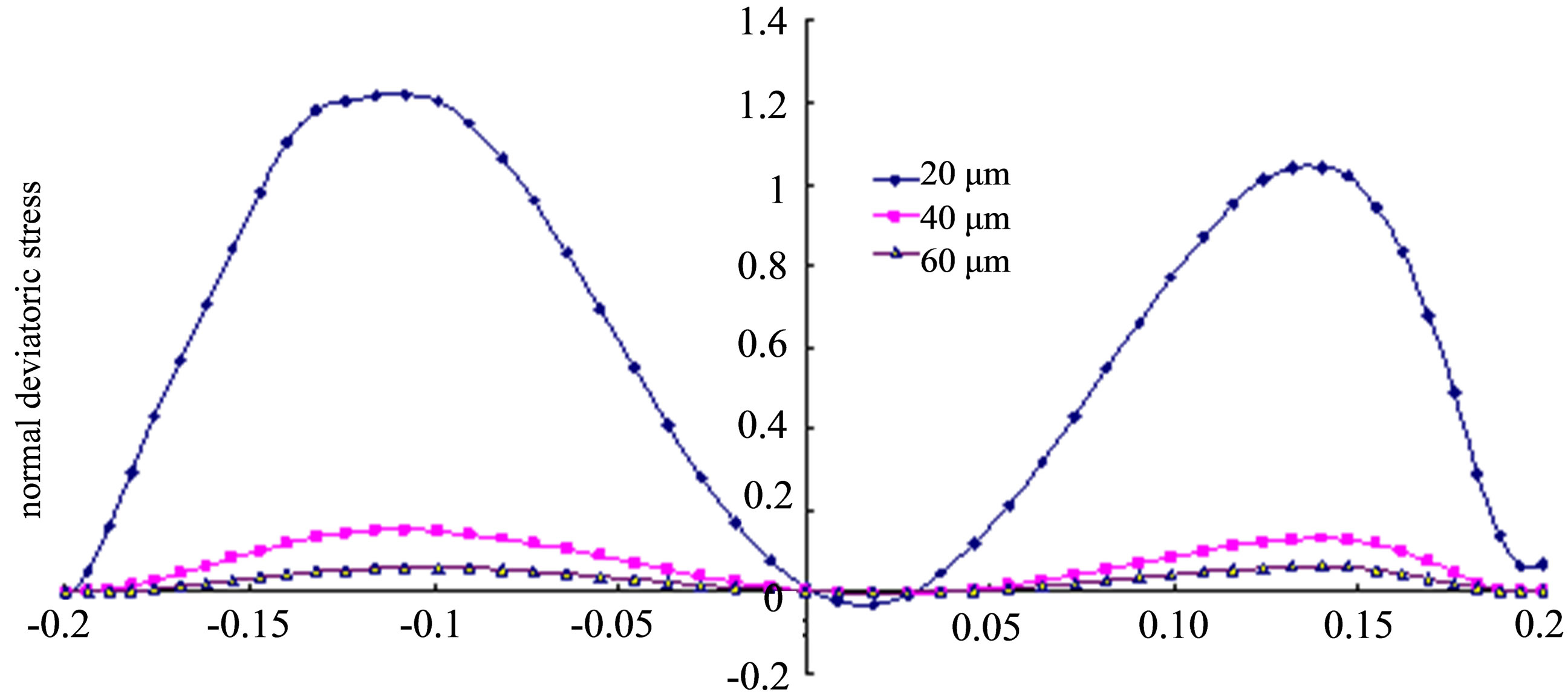 (b)
(b) (c)
(c)
Figure 3. The normal deviatoric stress acting on the residual oil under different permeability micro pores (pressure is positive, tension is negative); (a) Constant velocity (We = 0.2); (b) Constant flow (We = 0.2); (c) Constant pressure gradient (We = 0.2).
susceptible to be displaced.
5. Conclusion
Using constant pressure gradient flooding, the greater the permeability is, the greater the force of residual oil acting by viscous-elastic fluid is; using constant flow rate or constant velocity flooding, the situation is just the opposite; as We increases, the force of viscous-elastic fluid acting on residual oil increases.
REFERENCES
- D. M.Wang, J. C. Cheng, Q. Y. Yang, et al., “ViscousElastic Polymer Can Increase Micro Scale Displacement in Cores,” SPE63227, 2000, pp. 2-8.
- H. J. Yin, D. M. Wang, H. Y. Zhong, et al., “Study on Flow Behaviors of Viscoelastic Polymer Solution in Micro Pore with Dead End,” SPE101950, 2006, pp. 4-15.
- H. F. Xia, D. M. Wang, Z. C. Liu, et al., “Mechanism of Viscous-Elastic Polymer Solution to Improve Microscopic Flooding Efficiency,” Acta Petrolei Sinica, Vol. 22, No. 4, 2001, pp. 60-65.
- S. F. Han, “Non-Newtonian Fluid Constitutive Equation and the Analytic Theory,” Science Press, Beijing, 2002.

