Open Journal of Fluid Dynamics
Vol.3 No.2(2013), Article ID:32626,6 pages DOI:10.4236/ojfd.2013.32005
Drilling Operation and Formation Damage
Department of Petroleum Engineering, Islamic Azad University, Firoozabad Branch, Firoozabad, Iran
Email: hooman.fallah2@gmail.com
Copyright © 2013 Hooman Fallah, Sara Sheydai. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 26, 2013; revised April 28, 2013; accepted May 6, 2013
Keywords: Formation Damage; Drilling Mud; Classical Filtration; Maximum Retention Function External Filter Cake
ABSTRACT
Transport of particle suspensions in oil reservoirs is an essential phenomenon in many oil industry processes. Solid and liquid particles dispersed in the drilling fluid (mud) are trapped by the rock (porous medium) and permeability decline takes place during drilling fluid invasion into reservoir resulting in formation damage. The formation damage due to mud filtration is explained by erosion of external filter cake. Nevertheless, the stabilization is observed in core floods, which demonstrates internal erosion. A new mathematical model for detachment of particles is based on mechanical equilibrium of a particle positioned on the internal cake or matrix surface in the pore space. In the current work the analytical solution obtained to mud filtration with one particle capture mechanism with damage stabilization. The particle torque equilibrium is determined by the dimensionless ratio between the drag and normal forces acting on the particle. The maximum retention function of the dimensionless ratio closes system of governing equations for colloid transport through porous medium.
1. Introduction
Formation damage is an undesirable operational and economic problem that can occur during the various phases of oil and gas recovery from subsurface reservoirs including production, drilling, hydraulic fracturing, and work-over operations. Formation damage assessment, control, and remediation are among the most important issues to be resolved for efficient exploitation of hydrocarbon reservoirs [1].
Formation damage indicators include permeability impairment, skin, damage and decrease of well performance. Flow of suspensions in rocks with particle capture and consequent permeability impairment is an essential phenomenon in many oil industry processes. Particle capture by rock and permeability decline takes place during drilling fluid invasion into reservoir resulting in formation damage. It also occurs during fines migration, mostly in reservoirs with low consolidated sands and heavy oil.
Diagnosis of formation damage allows choosing the right damage removal technology during seawater injection to enhance the recovery factor of hydrocarbon reservoirs. The particle erosion was described by introduction of a new particle storage capacity function which is equal to maximum retained concentration versus dimensionless flow velocity. The particle storage capacity function is a reological characteristic that closes system of governing equations.
Deep bed filtration of fines with capture and permeability damage takes place near to production wells, in drilling operation. The particles in drilling fluid are captured by size exclusion (straining) or by different attachment mechanisms (electric forces, gravity segregation and diffusion). The analytical solution for deep bed filtration shows that for the case of the vanishing filtration function, the injectivity stabilizes when time tends to infinity.
The classical mathematical model for suspension flow in rocks consists of particle balance and capture kinetics equations [2]. It is assumed that the mean particle speed is equal to carrier water velocity.
Internal filtration is the phenomenon describing the capture of suspended particles and droplets of a suspension flowing through a porous medium. Internal filtration of suspended and precipitating solids and the associated formation damage constitute fundamental components of the productivity decline problem. The phenomenon is complex and multiple parameters play a role. The characteristics of the porous medium play a role; for example the size distribution of the pore throats, the connectivity of the pore bodies and the surface chemistry of the grains comprising the porous medium.
External filter cake is the term used to describe the particles retained at the interface of porous medium. The retention of particles occurs due to different phenomena including size exclusion; i.e. at the wellbore (Barkman and Davidson 1972) [3]. An alternative mechanism for the development of an external filter cake is that of transitioning from internal filtration to external filter cake buildup. An example of external filter cake build-up due to size exclusion is that associated with drilling. When drilling, the circulating mud is designed to prevent fluid leak-off with minimal internal filtration by forming external filter cakes due to size exclusion. Such cakes are easier to remedy and stimulate, whereas internal filtration is more difficult to remedy.
2. Literature Review
Davison et al. [4] conducted experiments by following colloidal silica suspension through three types of core plugs taken from Berea, Noxie and Cleveland sandstones. Their results show that particles initially pass through the larger openings in the core and are stopped gradually by a combination of effects of sedimentation, direct interception and surface deposition. The plugging of the core appears to be a combination of internal blockage of pores and cake buildup. They found that the larger particles initiate cake formation.
In most cases, the core itself was only partially plugged, but the experimental cake formed at the face of the core restricted the flow of the suspension. Davidson [4] conducted experiments on the flow of particles suspensions through porous media. A major finding of this work was that the velocity required to prevent particle deposition is reversely related to the particle size. However, it is the first indication in the literature that there is a relationship between particle movement through porous media and linear flow velocity.
Todd et al. [5] conducted particle-plugging experiments on three different core materials. The result of these studies indicates that significant permeability impairment can be caused by inorganic solids, even in dilute system.
Todd [6] used aluminum oxide particles in the size ranges 0 to 3, 4 to 6, and 8 to 1 microns. They found the following: 1) The overall damage is related to the mean pore-throat size; 2) The cores damaged with 0 to 3 micron suspensions exhibit damage throughout their entire length; and 3) As particle size increases, the damage is gradually shifted toward the injection end of the core.
When suspended particles in a carrier fluid are flowed through a porous medium, the operative plugging mechanism depends on the characteristics of the particles, the characteristics of the formation and the nature of the interaction between the particles and the various reservoir materials.
The particle/pore size ratio is the most important parameter in the filtration process. It has been found that larger particle/pore size ratios tend to cause rapid, but shallow, damage.
Particle retention and formation damage accumulation take place according to the classical suspension filtration theory until the retention concentration reaches the critical value defined by the torque balance, from now on the particles do not deposit any more.
3. Particle Mechanical Equilibrium and Maximum Retention Concentration Function
Particle capture by the rock takes place until the drog force moment, acting on the particle on the surface of the growing internal cake by moving water exceeds the attractive normal force moment.
Particle capture and filling the space in a pore results in the porosity decrease and in increase of interstitial velocity of fluid in a pore, provided the same injection rates maintained. Consequently increases the drag force acting on a particle on the internal cake surface from moving fluid (Figure 1).
According to Jiao and Sharma [7] for particle equilibrium on the cake surface as the equality torques for electric and drag forces:
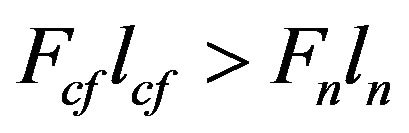 (1)
(1)
Here the normal force is a total of electric and lifting forces.
Drag force is the general expression for the drag force acting on a spherical particle in flow between two parallel plates. The lever arms for drag and normal force have the same order of magnitude. Their ratio is equal to 30.5 for the case of equal spherical particles (Figure 1).
Appendix A provides all the above-mentioned forces.
The flow velocity and the pressure gradient are linked by the Darcy law. According the Darcy equation for fluid (Mud Filtrate) flow through porous media:
 (2)
(2)
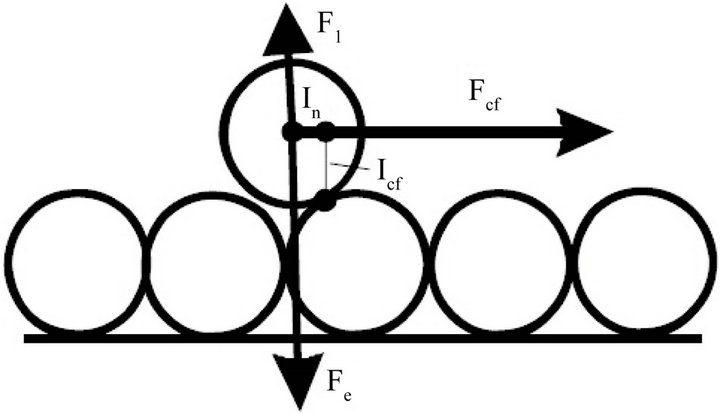
Figure 1. Forces and force moment balance on the particle at the cake surface.
Here we introduce the dimensionless parameter which is ratio between the drag force and the normal force:
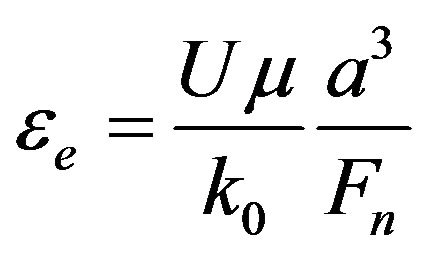 (3)
(3)
As it follows from the torque balance and the velocity dependencies of drag and lifting forces, for each flow velocity there does not exist a maximum retained concentration that correspond to equilibrium of torques acting on a single particle.
The maximum retention concentration becomes a function of the particle dislodging number, expressing the relationship between 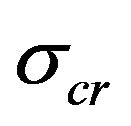 and ε:
and ε:
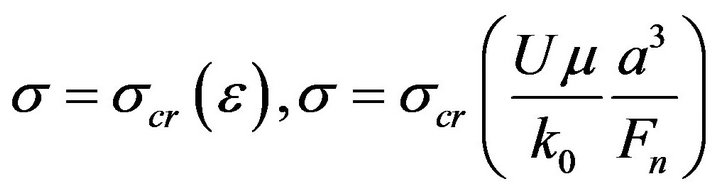 (4)
(4)
The higher is the velocity U, the higher is the numerator in the expression (4) for the erosion number , the higher is the lifting force and the lower is the denominator in (4). So the erosion number is a monotonically increasing function of U. The dependence (4) is called the storage capacity function.
, the higher is the lifting force and the lower is the denominator in (4). So the erosion number is a monotonically increasing function of U. The dependence (4) is called the storage capacity function.
4. Basic Equation for Classical Filtration Theory with Retained Particle Release
The particle capture rate is given by the classical filtration theory [8] assuming that retention rate is proportional to particle flux cU, i.e.
 (5)
(5)
Here the deposited concentration is significantly lower than the concentration of vacancies in the pore space which means that the filtration coefficient  is constant.
is constant.
The mathematical mass balance for suspended and retained particles during 1 d linear filtration is
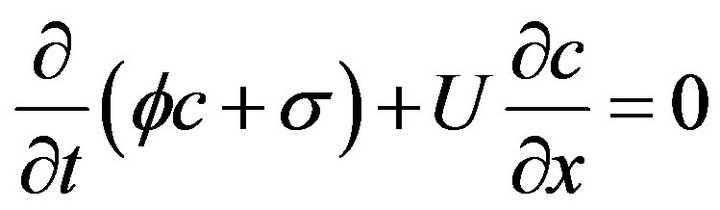 (6)
(6)
The Darcy equation accounting for formation damage describes the flux and pressure distribution
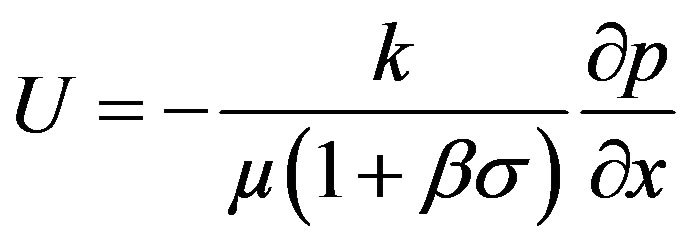 (7)
(7)
The derivations of dimensionless system along with initial and boundary data are presented in Appendix B.
5. Analytical Solution for Erosive Classical Filtration with One Capture Mechanism for Constant Rate Mud Invasion
The initial boundary value problem (B-6,7) for system (B-2,5) allows for exact analytical solution. Below the solution is derived.
This solution for the under saturated case  is well known [9]. Expressing suspension concentration from (B-3)
is well known [9]. Expressing suspension concentration from (B-3)
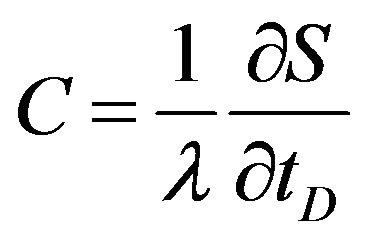 (8)
(8)
Substituting it into (B-2) and integrating in 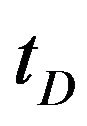 with regards to initial condition (B-6), we obtain
with regards to initial condition (B-6), we obtain
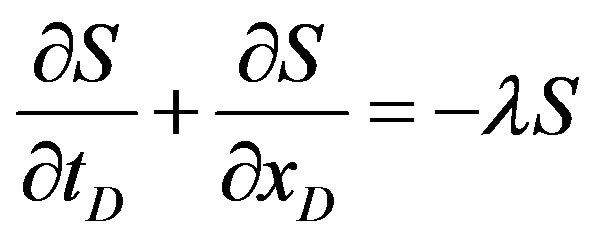 (9)
(9)
From kinetics Equation (B-3) and boundary condition (B-7) we derive the following boundary condition for retained concentration:
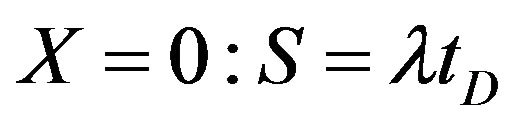 (10)
(10)
The solution is obtained by method of characteristics [9]. Both concentrations are zero ahead of the concentration front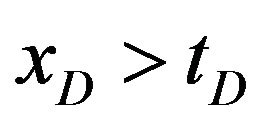 :
:
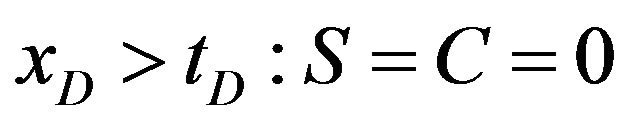 (11)
(11)
Equation (9) in characteristic form is
 (12)
(12)
That with boundary condition (10) leads to the solution
 (13)
(13)
At the moment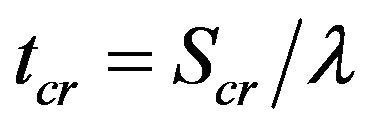 , the retained concentration at the inlet
, the retained concentration at the inlet  reaches the critical value. Appears a front
reaches the critical value. Appears a front 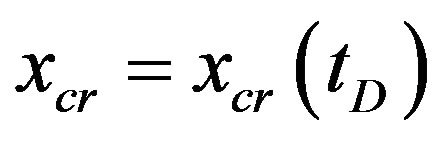 along
along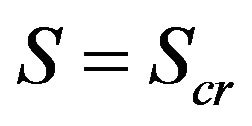 . Further retention behind the front which does not happen:
. Further retention behind the front which does not happen:
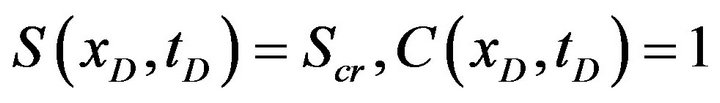 (14)
(14)
Differentiate the condition of  along the erosion front
along the erosion front
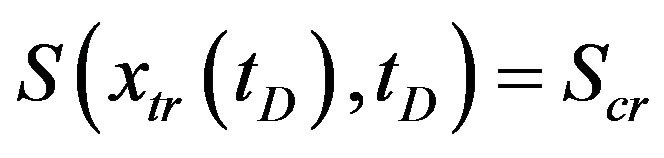 (15)
(15)
by :
:
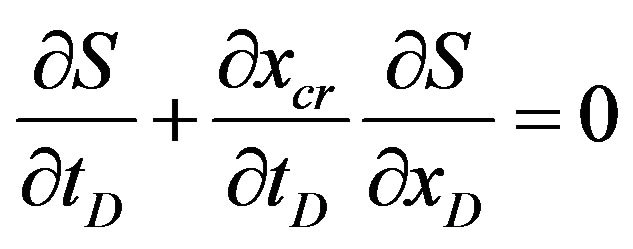 (16)
(16)
Equation (16) contains three unknowns: both partial derivatives of S and velocity of the erosion front.
Equation (9) also contains two partial derivatives of S.
Let us derive the condition of particle flux continuity on the erosion front :
:

As it follows from rate Equation (B-3), concentration S is always continuous. Therefore, 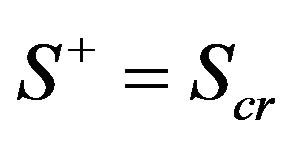 on the erosion front, and the balance condition on the shock becomes
on the erosion front, and the balance condition on the shock becomes

Which leaves two possibilities: either  or C is continuous. Since velocity of erosion front is less than unity, the suspended concentration is continuous. Therefore,
or C is continuous. Since velocity of erosion front is less than unity, the suspended concentration is continuous. Therefore, 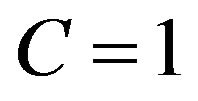 along the erosion front. It allows calculating the time derivative of S:
along the erosion front. It allows calculating the time derivative of S:
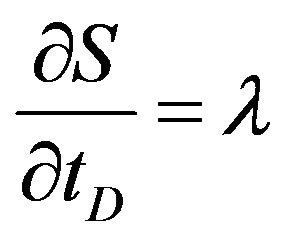 (17)
(17)
Equations (9), (16) and (17) from a linear system of three eqs. for three unknowns. The solution is
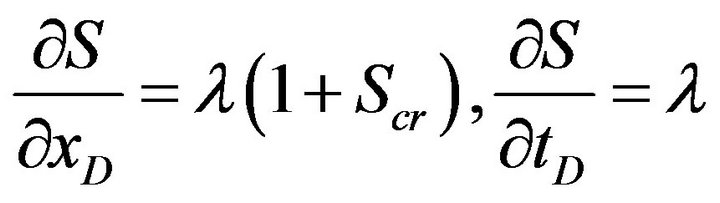 (18)
(18)
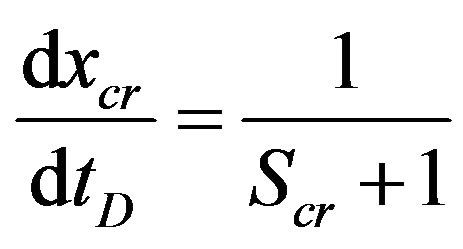 (19)
(19)
Finally, we obtain equation for erosion front:
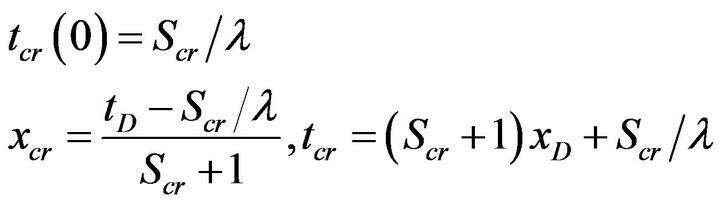 (20)
(20)
Above expressions define the analytical model for injection of suspension with the constant rate accounting for retained particle dislodging by drag force.
Introduction of just one new parameter-maximum retained concentrationinto a classical suspension filtration model allows for significant enrichment of the physics schema for suspension transport and retention.
The analytical model developed allows to perfectly match the experimental impedance curve and calculated from it three injectivity parametersfiltration and formation damage coefficients, and also the maximum retention concentration.
6. Conclusion
Near wellbore mud filtrate during drilling operation and the resulting formation damage are amongst the most important problems involving the petroleum reservoir exploitation.
The suspension mud model with stabilized retention concentration is based on the assumption that for each flow velocity there does exists the maximum amount of retention particles that electric-molecular forces can keep. The dimensionless erosion number, which is ratio between the cross flow drag force and the total of normal forces, is proportional to flow velocity. The stabilization phenomenon is characterized by so called storage capacity which is the maximum retention concentration versus erosion number. The maximum retention function of the dimensionless ratio closes system of governing equations for colloid transport through porous medium.
The analytical solution obtained to mud filtration with one particle capture mechanism with damage stabilization.
Pressure drop measurement during core flood by particle suspension allows for complete characterization of the filtration damage system, i.e., mud filtration and formation damage coefficients altogether with maximum retention concentration can be calculated.
REFERENCES
- F. Civan, “Reservoir Formation Damage (Fundamentals, Modeling, Assessment and Mitigation),” 2nd Edition, Gulf Professional Publishing, Houston, 2006.
- A. C. Payatakes, et al., “Application of Porous Medium Models to the Study of Deep Bed Filtration,” The Canadian Journal of Chemical Engineering, Vol. 52, No. 6, 1974, pp. 722-731. doi:10.1002/cjce.5450520605
- J. H. Barkman and D. H. Davidson, “Measuring Water Quality and Predicting Well Impairment,” Journal of Petroleum Technology, Vol. 24, No. 7, 1972, pp. 865-873.
- E. C. Davison, “Particle Transport in Sandstone,” SPE Annual Technical Conference and Exhibition, Denver, 12 October 1977.
- A. C. Todd, et al., “Review of Permeability Damage Stodies and Related North Sea Water Injection,” SPE International Symosium on Oilfield and Geothermal Chemistry, Dallas, 22-24 January 1979.
- A. C. Todd, et al., “The Application of Depth of Formation Damage Measurments in Predicted Water Injectivity Decline,” SPE Formation Damage Control Symposium, Bakersfield, 13-14 February 1984.
- D. Jiao and M. M. Sharma, “Mechanism of Cake Buildup in Crossflow Filtration of Colloidal Suspensions,” Journal of Colloidal and Interfacial Science, Vol. 162, No. 2, 1994, pp. 454-462. doi:10.1006/jcis.1994.1060
- J. P. Herzig, D. M. Leclerc and P. Le Goff, “Flow of Suspensions through Porous Media,” Journal of Industrial and Engineering Chemistry, Vol. 65, No. 5, 1970, pp. 8-35. doi:10.1021/ie50725a003
- S. Pang and M. M. Sharma, “A Model for Predicting Injectivity Decline in Water Injection Wells,” SPE Formation Evaluation, Vol. 12, No. 3, 1997, pp. 194-201.
Nomenclator
 : Drag force
: Drag force
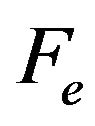 : Lifting force
: Lifting force
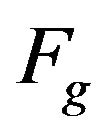 : Gravity force
: Gravity force
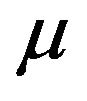 : Viscosity
: Viscosity
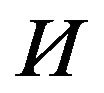 : Hamkar constant
: Hamkar constant
 : Filtration coefficient
: Filtration coefficient
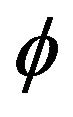 : Effective porosity
: Effective porosity
 : Volumetric concentration of suspended particles with respect to the volume
: Volumetric concentration of suspended particles with respect to the volume
 : Volumetric concentration of retained particles with respect to the bulk volume
: Volumetric concentration of retained particles with respect to the bulk volume
 : Surface to surface separation
: Surface to surface separation
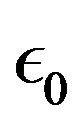 : Permittivity under vacuum
: Permittivity under vacuum
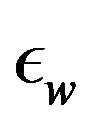 : Permittivity of the solute (water)
: Permittivity of the solute (water)
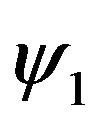 : Surface potentials of particles and collectors respectively
: Surface potentials of particles and collectors respectively
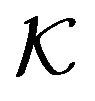 : Inverse Debye length
: Inverse Debye length
 : Difference between the densities of the suspended particles (hematite) and the suspending fluid (water)
: Difference between the densities of the suspended particles (hematite) and the suspending fluid (water)
Appendix A. Forces Acting on the Captured Particle on the Surface of Internal Cake on the Pore Wall
Consider forces which act on the captured particle (Figure 1): darg force  acting on the particle from bypassing viscous water; electric-molecular force
acting on the particle from bypassing viscous water; electric-molecular force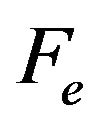 ; lifting force
; lifting force  and gravity
and gravity .
.
A general form of the crossflow drag force in HeleShaw flow in rectangular channel geometry with a single permeable wall is given as:
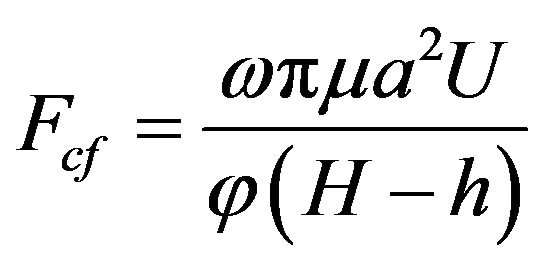 (A-1)
(A-1)
where  is proportionality factor in the range [10, 60],
is proportionality factor in the range [10, 60], 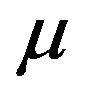 is the viscosity,
is the viscosity,  is the particle radius,
is the particle radius, 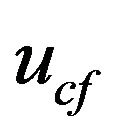 is the average crossflow velocity at a given cross-section,
is the average crossflow velocity at a given cross-section,  is the height of the channel, and h is the thickness of the cake at a given cross-section.
is the height of the channel, and h is the thickness of the cake at a given cross-section.
The electrostatic (a.k.a. surface or colloidal) force is directly proportional to the radius of the particles and is given by (10):
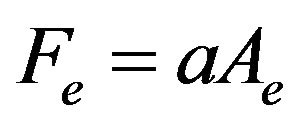 (A-2)
(A-2)
where:
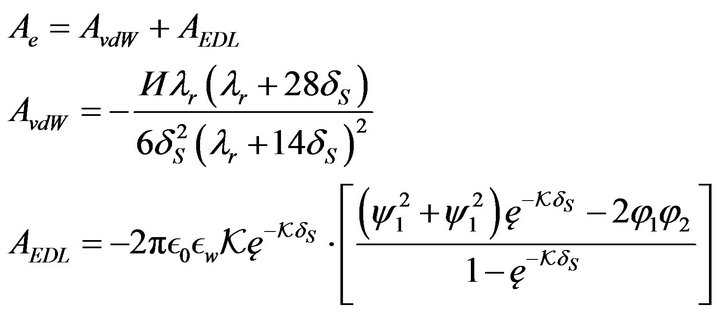
Here 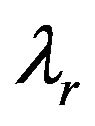 is the characteristic retardation wavelength of interaction and is often assumed to be
is the characteristic retardation wavelength of interaction and is often assumed to be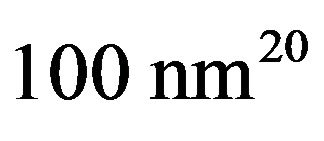 ,
,  is the Hamkar constant of the interacting media,
is the Hamkar constant of the interacting media, 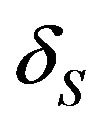 is the surface to surface separation,
is the surface to surface separation, 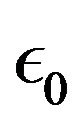 and
and 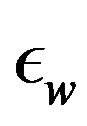 are the permittivity under vacuum and relative dielectric permittivity of the solute (water) respectively,
are the permittivity under vacuum and relative dielectric permittivity of the solute (water) respectively, 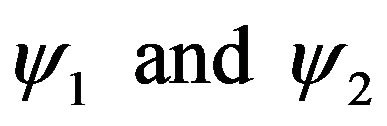 are the surface potentials of particles and collectors respectively and
are the surface potentials of particles and collectors respectively and 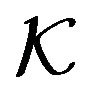 is the inverse Debye length.
is the inverse Debye length.
It should be noted that at certain salinities and pH values decreasing the surface to surface separation 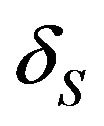 between one hematite particle and the other from infinity to zero yields two energy minima. The secondary minimum usually corresponds to a separation of >15 nm while the primary minimum corresponds to surface to surface separation of 4 nm. By considering only the forces acting along the axis parallel to the permeate force, a check can be made to see whether the particle has enough energy to overcome the activation energy and position itself within the primary minimum.
between one hematite particle and the other from infinity to zero yields two energy minima. The secondary minimum usually corresponds to a separation of >15 nm while the primary minimum corresponds to surface to surface separation of 4 nm. By considering only the forces acting along the axis parallel to the permeate force, a check can be made to see whether the particle has enough energy to overcome the activation energy and position itself within the primary minimum.
The general force of lifting force is given by:
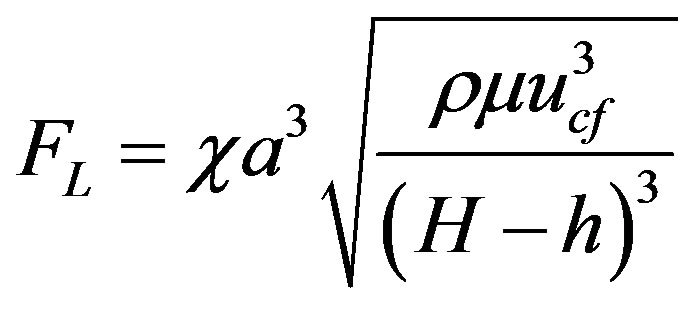 (A-3)
(A-3)
where  was given as 89.5 by Kang et al. (11).
was given as 89.5 by Kang et al. (11).
The gravity force is given by:
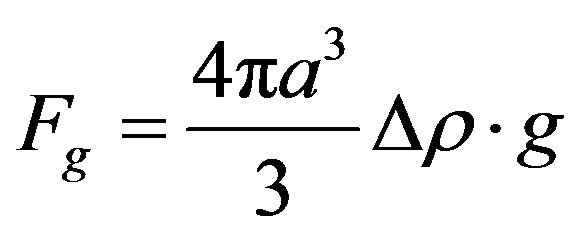 (A-4)
(A-4)
where  is the difference between the densities of the suspended particles (hematite) and the suspending fluid (water). The normal force in Figure 1 is a total of electric molecular and lifting forces.
is the difference between the densities of the suspended particles (hematite) and the suspending fluid (water). The normal force in Figure 1 is a total of electric molecular and lifting forces.
Appendix B. Basic Equations for Suspension Transport with One Particle Capture Mechanisms and Deposit Erosion
Let us introduce dimensionless length and time into the dimensionless system for classical filtration with particle dislodging (7):
 (B-1)
(B-1)
The system (7) takes the form:
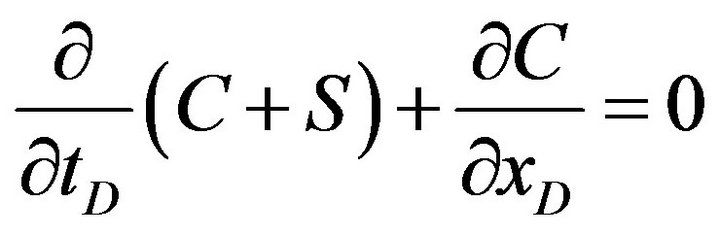 (B-2)
(B-2)
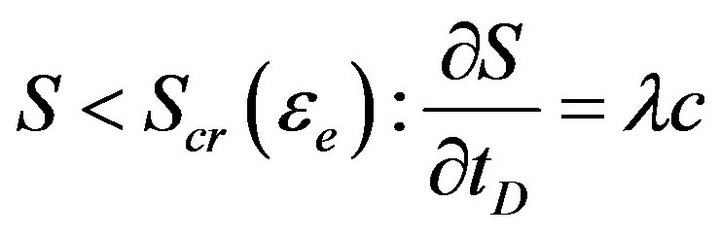 (B-3)
(B-3)
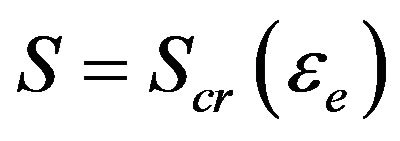 (B-4)
(B-4)
Equations (B-3) and (B-4) can be written in the generalized form
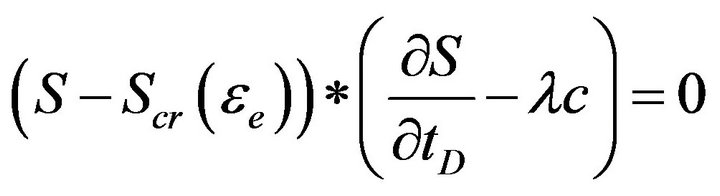 (B-5)
(B-5)
Initial condition for system (B-2,5) correspond to absence of either suspended or deposited particles in the core before the suspension injection
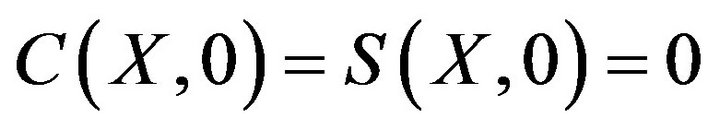 (B-6)
(B-6)
Boundary condition corresponds to a given inlet concentration
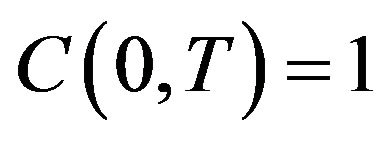 (B-7)
(B-7)
System (B-2,5) subject to initial and boundary conditions (B-6,7) describes the process of suspension injection into a virgin core.

