Open Journal of Fluid Dynamics
Vol. 3 No. 1 (2013) , Article ID: 29374 , 14 pages DOI:10.4236/ojfd.2013.31002
Combined Effects of Hall Current and Radiation on MHD Free Convective Flow in a Vertical Channel with an Oscillatory Wall Temperature
1Department of Applied Mathematics, Vidyasagar University, Midnapore, India
2Department of Mathematics, University of Gour Banga, English Bazar, India
Email: jana261171@yahoo.co.in
Received December 11, 2012; revised January 15, 2013; accepted January 26, 2013
Keywords: Hall Current; MHD Free Convection; Radiation; Prandtl Number; Grashof Number; Frequency Parameter; Impulsive Motion; Accelerated Motion
ABSTRACT
The combined effects of Hall current and radiation on an unsteady MHD free convective flow of a viscous incompressible electrically conducting fluid in a vertical channel with an oscillatory wall temperature have been studied. We have considered two different cases 1) flow due to the impulsive motion of one of the channel walls and 2) flow due to the accelerated motion of one of the channel walls. The governing equations are solved analytically using the Laplace transform technique. It is found that the primary velocity and the magnitude of the secondary velocity increased with an increase in Hall parameter for the impulsive as well as the accelerated motions of one of the channel walls. An increase in either radiation parameter or frequency parameter leads to decrease in the primary velocity and the magnitude of the secondary velocity for the impulsive as well as accelerated motions of one of the channel walls. The fluid temperature decreases with an increase in radiation parameter. Further, the shear stresses at the left wall reduce with an increase in either radiation parameter or frequency parameter for the impulsive as well as the accelerated motions of one of the channel wall.
1. Introduction
The mechanism of conduction in ionized gases in the presence of a strong magnetic field is different from that in metallic substance. The electric current in ionized gases is generally carried by electrons, which undergos successive collisions with other charged or neutral particles. In the ionized gases, the current is not proportional to the applied potential except when the field is very weak in an ionized gas where the density is low and the magnetic field is very strong, the conductivity normal to the magnetic field is reduced due to the free spiraling of electrons and ions about the magnetic lines of force before suffering collisions and a current is induced in a direction normal to both electric and magnetic fields. This phenomenon, well known in the literature, is called the Hall effect. The study of hydromagnetic flows with Hall currents has important engineering applications in problems of magnetohydrodynamic generators and of Hall accelerators as well as in flight magnetohydrodynamics. It is well known that a number of astronomical bodies posses fluid interiors and magnetic fields. It is also important in the solar physics involved in the sunspot development, the solar cycle and the structure of magnetic stars. In space technology applications and at higher operating temperatures, radiation effects can be quite significant. The radiative convective flows are frequently encountered in many scientific and environmental processes, such as astrophysical flows, water evaporation from open reservoirs, heating and cooling of chambers, and solar power technology. The unsteady hydromagnetic flow of a viscous incompressible electrically conducting fluid through a vertical channel is of considerable interest in the technical field due to its frequent occurrence in industrial and technological applications. The Hall effects on the flow of ionized gas between parallel plates under transverse magnetic field have been studied by Sato [1]. Miyatake and Fujii [2] have discussed the free convection flow between vertical plates—one plate isothermally heated and other thermally insulated. Natural convection flow between vertical parallel plates—one plate with a uniform heat flux and the other thermally insulated has been investigated by Tanaka et al. [3]. Gupta and Gupta [4] have studied the radiation effect on hydromagnetic convection in a vertical channel. Hall effects on the hydromagnetic convective flow through a vertical channel with conducting walls have been investigated by Dutta and Jana [5]. The unsteady hydromagnetic free convective flow with radiative heat transfer in a rotating fluid has been described by Bestman and Adjepong [6]. Joshi [7] has studied the transient effects in natural convection cooling of vertical parallel plates. Singh [8] have described the natural convection in unsteady Couette motion. Singh et al. [9] have studied the unsteady free convective flow between two vertical parallel plates. The natural convection in unsteady MHD Couette flow with heat and mass transfers has been analyzed by Jha [10]. Narahari et al. [11] have studied the unsteady free convective flow between long vertical parallel plates with constant heat flux at one boundary. The unsteady free convective flow in a vertical channel due to symmetric heating have been described by Jha et al. [12]. Singh and Paul [13] have studied the unsteady natural convective between two vertical walls heated/cooled asymmetrically. Sanyal and Adhikari [14] have studied the effects of radiation on MHD vertical channel flow. The radiation effects on MHD Couette flow with heat transfer between two parallel plates have been examined by Mebine [15]. Grosan [16] has studied the thermal radiation effect on the fully developed mixed convective flow in a vertical channel. Guria and Jana [17] have discussed Hall effects on the hydromagnetic convective flow through a rotating channel under general wall conditions. Jha and Ajibade [18] have studied the unsteady free convective Couette flow of heat generating/absorbing fluid. Effects of thermal radiation and free convection currents on the unsteady Couette flow between two vertical parallel plates with constant heat flux at one boundary have been studied by Narahari [19]. Rajput and Sahu [20] have studied the unsteady free convection MHD flow between two long vertical parallel plates with constant temperature and variable mass diffusion. Das et al. [21] have studied the radiation effects on free convection MHD Couette flow started exponentially with variable wall temperature in the presence of heat generation. The effect of radiation on transient natural convection flow between two vertical walls have been described by Mandal et al. [22]. Das et al. [23] have studied the radiation effects on unsteady MHD free convective Couette flow of heat generation/absorbing fluid. The effects of radiation on MHD free convective Couette flow in a rotating system have been discussed by Sarkar et al. [24]. Sarkar et al. [25] have studied an oscillatory MHD free convective flow between two vertical walls in a rotating system.
The aim of the present paper is to study the combined effects of Hall current and radiation on the unsteady MHD free convective flow of a viscous incompressible electrically conducting fluid in a vertical channel with an oscillatory wall temperature of one of the channel walls. It is found that the primary velocity  and the magnitude of the secondary velocity
and the magnitude of the secondary velocity  decrease with an increase in either radiation parameter
decrease with an increase in either radiation parameter  or frequency parameter
or frequency parameter  or Prandtl number
or Prandtl number 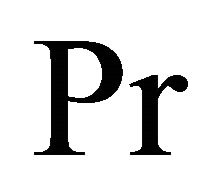 for the impulsive as well as the accelerated motions of one of the channel walls. It is also observed that the primary velocity
for the impulsive as well as the accelerated motions of one of the channel walls. It is also observed that the primary velocity 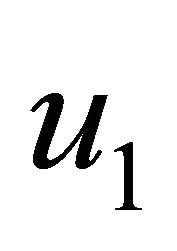 and the magnitude of the secondary velocity
and the magnitude of the secondary velocity 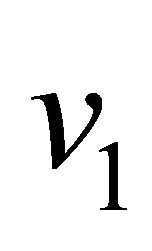 increase with an increase in either Hall parameter
increase with an increase in either Hall parameter 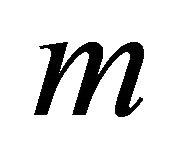 or Grashof number
or Grashof number 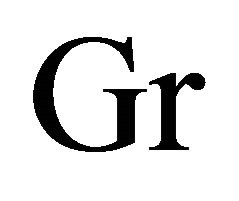 or time
or time  for the impulsive as well as accelerated motions. An increase in Grashof number
for the impulsive as well as accelerated motions. An increase in Grashof number 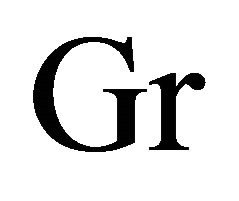 leads to fall the fluid velocity components. An increase in the radiation parameter
leads to fall the fluid velocity components. An increase in the radiation parameter 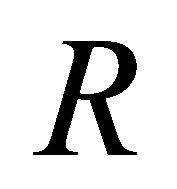 leads to increase the fluid temperature. Further, the shear stress
leads to increase the fluid temperature. Further, the shear stress 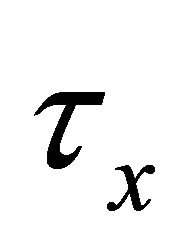 at the wall
at the wall  due to the primary flow and the absolute value of the shear stress
due to the primary flow and the absolute value of the shear stress  at the wall
at the wall 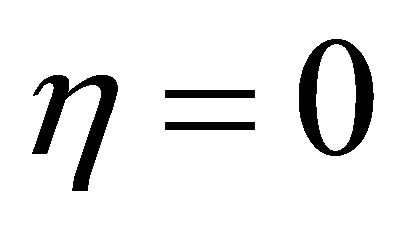 due to the secondary flow decrease for the impulsive as well as accelerated motions of one of the channel walls with an increase in radiation parameter
due to the secondary flow decrease for the impulsive as well as accelerated motions of one of the channel walls with an increase in radiation parameter . The rate of heat transfer
. The rate of heat transfer  at the wall
at the wall  decreases while the rate of heat transfer
decreases while the rate of heat transfer 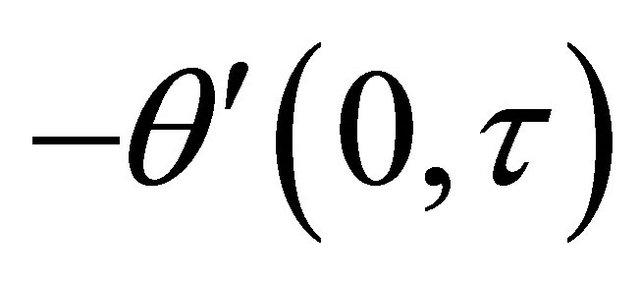 at the wall
at the wall  increases with an increase in Prandtl number
increases with an increase in Prandtl number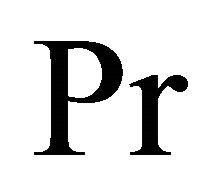 .
.
2. Formulation of the Problem and Its Solution
Consider the unsteady MHD flow of a viscous incompressible electrically conducting radiative fluid between two infinitely long vertical parallel walls separated by a distance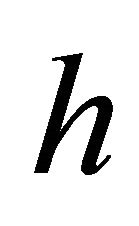 . The flow is set up by the buoyancy force arising from the temperature gradient. Choose a Cartesian co-ordinates system with the x-axis along the channel wall at
. The flow is set up by the buoyancy force arising from the temperature gradient. Choose a Cartesian co-ordinates system with the x-axis along the channel wall at  in the vertically upward direction, the y-axis perpendicular to the channel walls and z-axis is normal to the xy-plane (see Figure 1). Initially, at time
in the vertically upward direction, the y-axis perpendicular to the channel walls and z-axis is normal to the xy-plane (see Figure 1). Initially, at time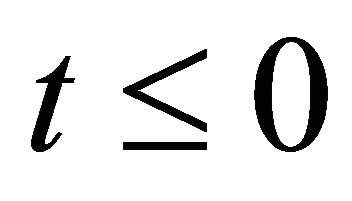 , the two walls and the fluid are assumed to be at the same temperature
, the two walls and the fluid are assumed to be at the same temperature 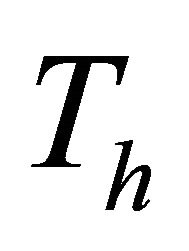 and stationary. At time
and stationary. At time , the wall at
, the wall at  starts to move in its own plane with a velocity
starts to move in its own plane with a velocity  and its temperature is raised to
and its temperature is raised to  whereas the wall at
whereas the wall at  is stationary and maintained at a constant temperature
is stationary and maintained at a constant temperature , where
, where  is the frequency of the temperature oscillations. A uniform transverse magnetic field
is the frequency of the temperature oscillations. A uniform transverse magnetic field 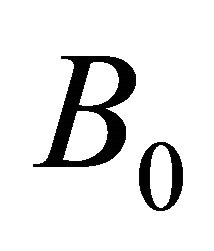 is applied perpendicular to the channel walls. We assume that the flow is laminar and the pressure gradient term in the momentum equation can be neglected. It is assumed that the effect of viscous and Joule dissipations are negligible. It is also assumed that the radiative heat flux in the x-direction is negligible as compared to that in the y-direction. As the channel walls are infinitely long, the velocity field and temperature distribution are functions of y and t only.
is applied perpendicular to the channel walls. We assume that the flow is laminar and the pressure gradient term in the momentum equation can be neglected. It is assumed that the effect of viscous and Joule dissipations are negligible. It is also assumed that the radiative heat flux in the x-direction is negligible as compared to that in the y-direction. As the channel walls are infinitely long, the velocity field and temperature distribution are functions of y and t only.
Under the usual Boussinesq approximation, the flow is governed by the following Navier-Stokes equations
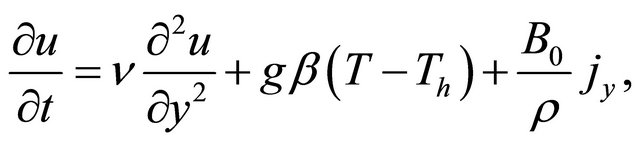 (1)
(1)

Figure 1. Geometry of the problem.
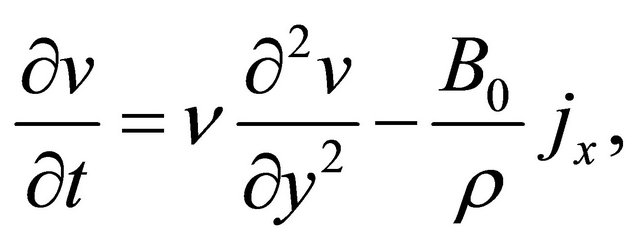 (2)
(2)
where 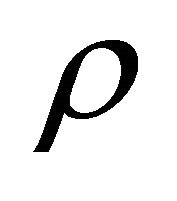 is the fluid density,
is the fluid density, 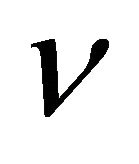 the kinematic viscosity,
the kinematic viscosity, 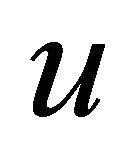 and
and 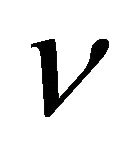 are fluid velocity components and
are fluid velocity components and 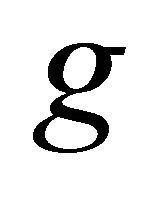 the acceleration due to gravity.
the acceleration due to gravity.
The energy equation is
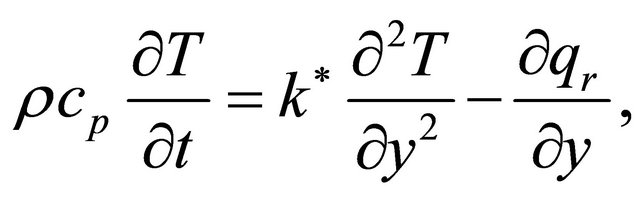 (3)
(3)
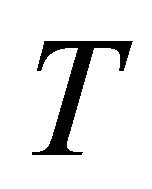 the fluid temperature,
the fluid temperature, 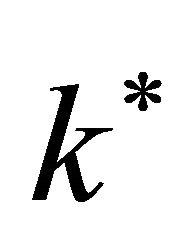 the thermal conductivity,
the thermal conductivity,  the specific heat at constant pressure and
the specific heat at constant pressure and 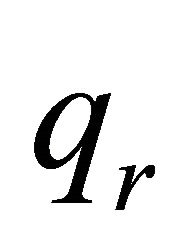 the radiative heat flux.
the radiative heat flux.
The initial and boundary conditions for the velocity and temperature distributions are
 (4)
(4)
It has been shown by Cogley et al. [26] that in the optically thin limit for a non-gray gas near equilibrium, the following relation holds
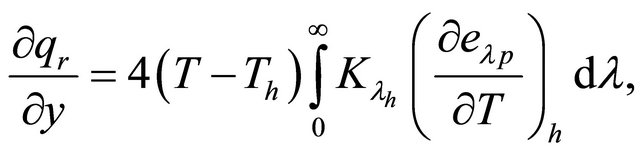 (5)
(5)
where 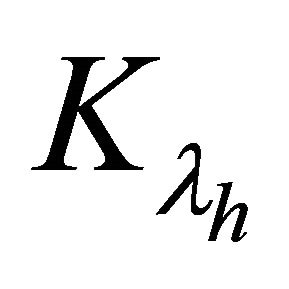 is the absorption coefficient,
is the absorption coefficient,  is the wave length,
is the wave length, 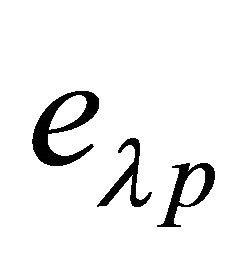 is the Planck’s function and subscript
is the Planck’s function and subscript 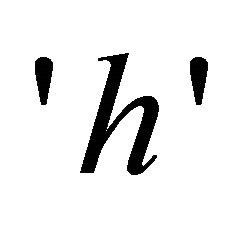 indicates that all quantities have been evaluated at the temperature
indicates that all quantities have been evaluated at the temperature 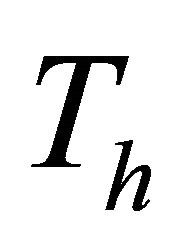 which is the temperature of the walls at time
which is the temperature of the walls at time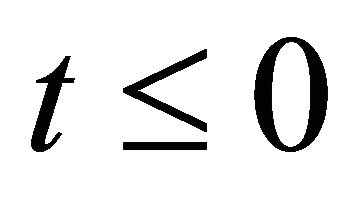 . Thus, our study is limited to small difference of wall temperatures to the fluid temperature.
. Thus, our study is limited to small difference of wall temperatures to the fluid temperature.
On the use of the Equation (5), the Equation (3) becomes
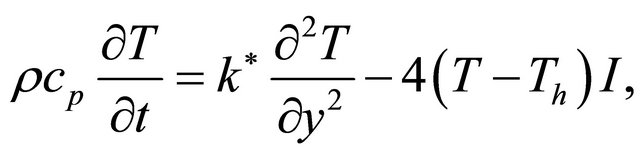 (6)
(6)
where
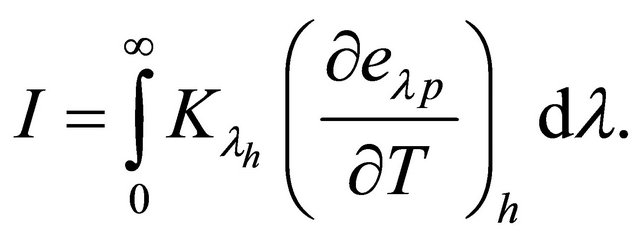 (7)
(7)
The generalized Ohm’s law, on taking Hall currents into account and neglecting ion-slip and thermo-electric effect, is (see Cowling [27])
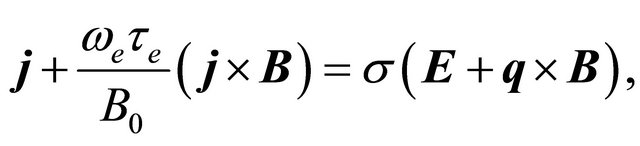 (8)
(8)
where  is the current density vector,
is the current density vector,  the magnetic field vector,
the magnetic field vector,  the electric field vector,
the electric field vector, 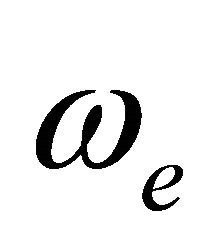 the cyclotron frequency,
the cyclotron frequency,  the electrical conductivity of the fluid and
the electrical conductivity of the fluid and 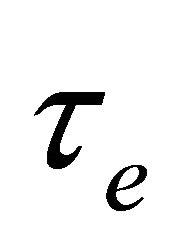 the collision time of electron.
the collision time of electron.
We shall assume that the magnetic Reynolds number for the flow is small so that the induced magnetic field can be neglected. This assumption is justified since the magnetic Reynolds number is generally very small for partially ionized gases. The solenoidal relation  for the magnetic field gives
for the magnetic field gives 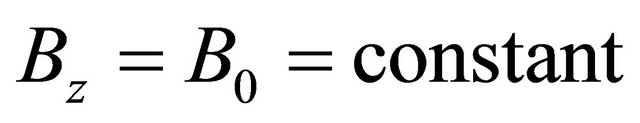 everywhere in the fluid where
everywhere in the fluid where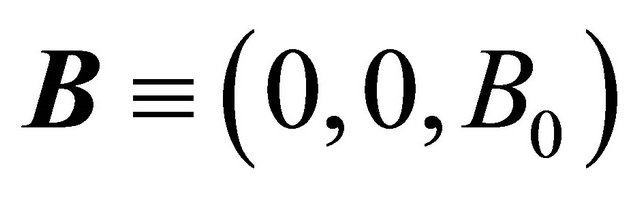 . Further, if
. Further, if 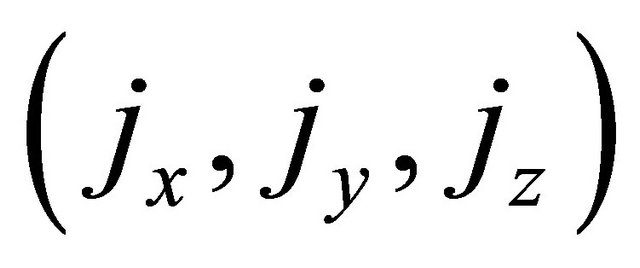 be the components of the current density
be the components of the current density , then the equation of the conservation of the current density
, then the equation of the conservation of the current density 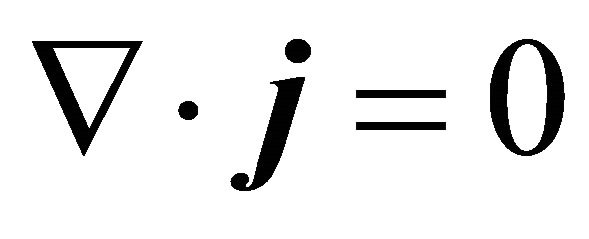 gives
gives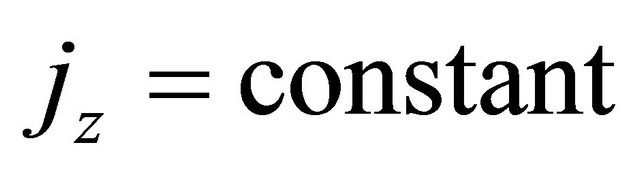 . This constant is zero since
. This constant is zero since 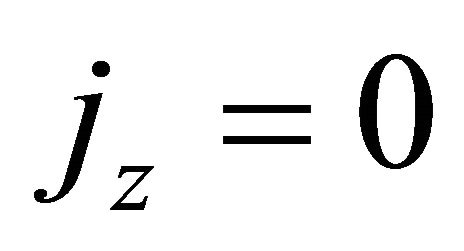 at the walls which are electrically nonconducting. Thus
at the walls which are electrically nonconducting. Thus 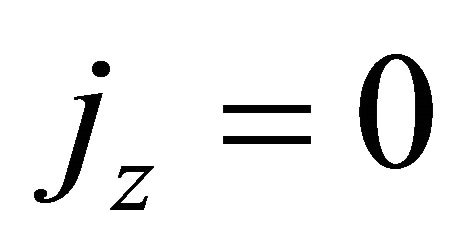 everywhere in the flow. Since the induced magnetic field is neglected, the Maxwell’s equation
everywhere in the flow. Since the induced magnetic field is neglected, the Maxwell’s equation 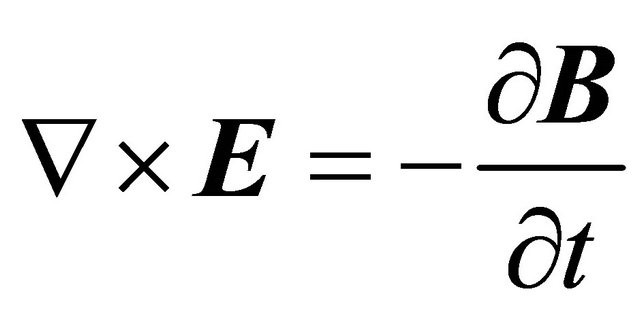 becomes
becomes  which gives
which gives  and
and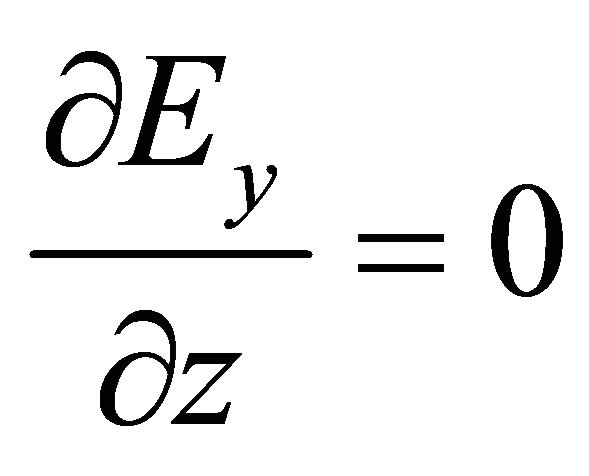 . This implies that
. This implies that
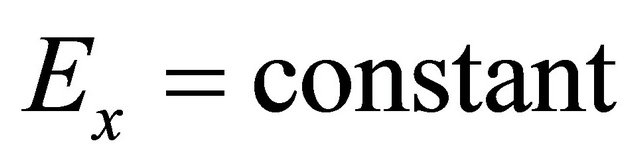 and
and 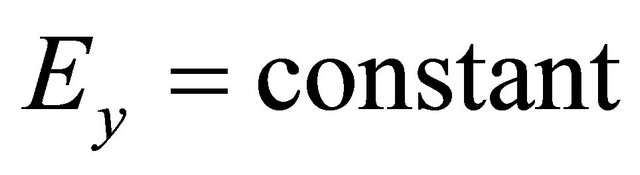 everywhere in the flow. We choose this constants equal to zero, i.e.
everywhere in the flow. We choose this constants equal to zero, i.e. .
.
In view of the above assumption, the Equation (8) gives
 (9)
(9)
 (10)
(10)
where 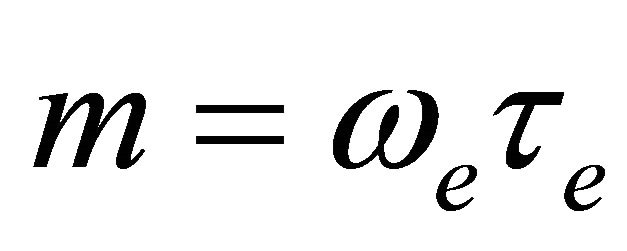 is the Hall parameter.
is the Hall parameter.
Solving (9) and (10) for  and
and , we have
, we have
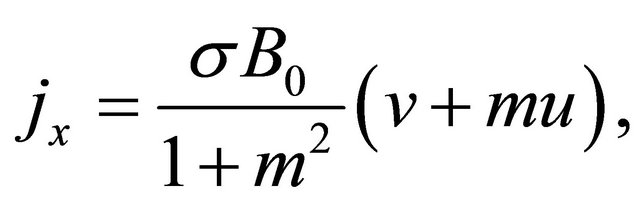 (11)
(11)
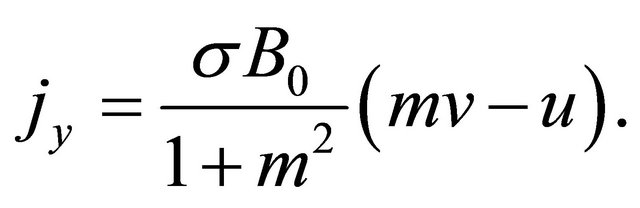 (12)
(12)
On the use of (11) and (12), the momentum Equations (1) and (2) along xand y-directions become
 (13)
(13)
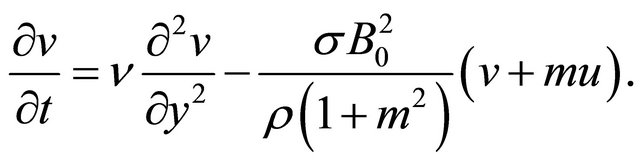 (14)
(14)
Introducing non-dimensional variables
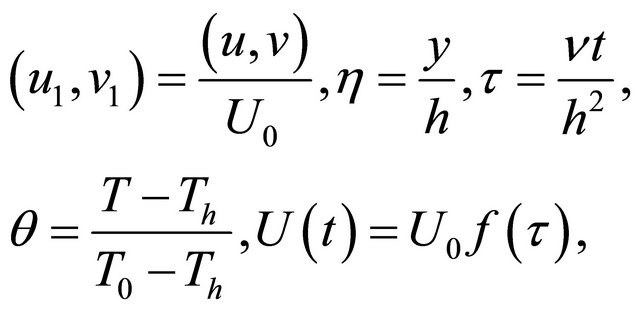 (15)
(15)
Equations (6), (13) and (14) become
 (16)
(16)
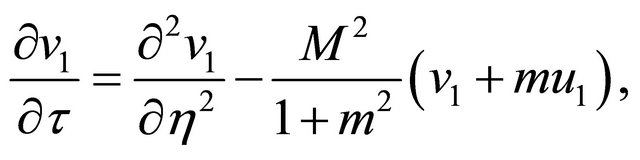 (17)
(17)
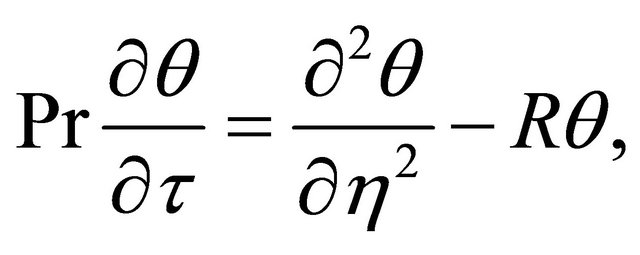 (18)
(18)
where  is the magnetic parameter,
is the magnetic parameter, 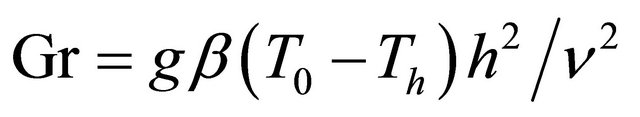 the Grashof number,
the Grashof number, 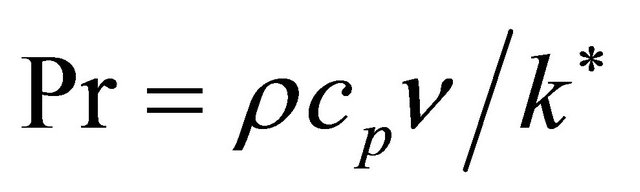 the Prandtl number and
the Prandtl number and 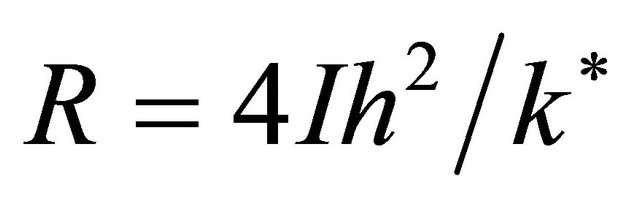 the radiation parameter.
the radiation parameter.
The initial and boundary conditions (4) become
 (19)
(19)
where  is the frequency parameter.
is the frequency parameter.
Combining Equations (16) and (17), we get
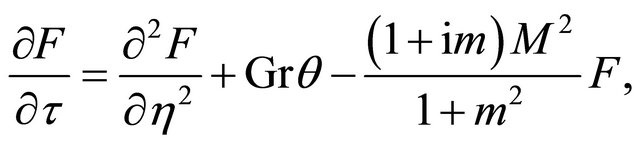 (20)
(20)
where
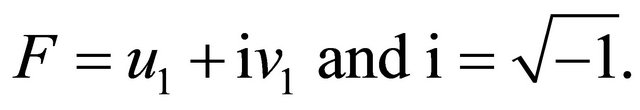 (21)
(21)
The initial and boundary conditions for  are
are
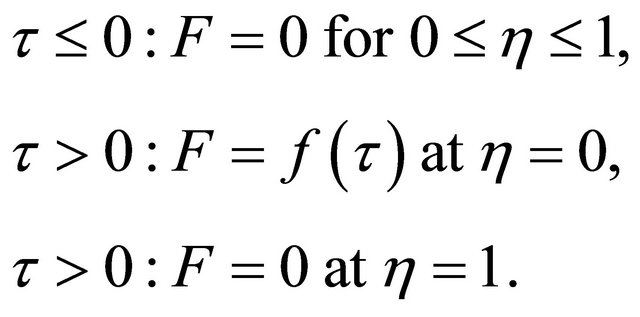 (22)
(22)
Taking the Laplace transform of Equations (20) and (18) and on the use of (19) and (22), we have
 (23)
(23)
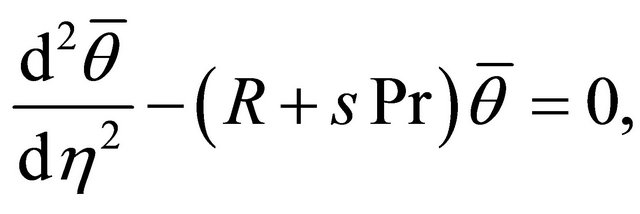 (24)
(24)
where
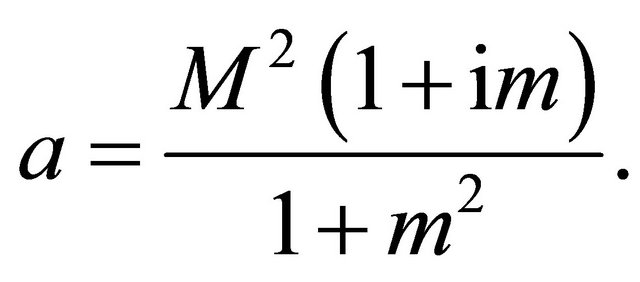 (25)
(25)
The initial and boundary conditions for 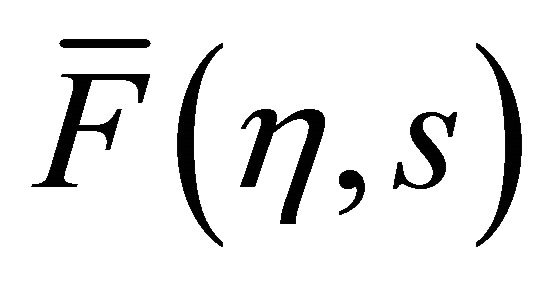 and
and  are
are
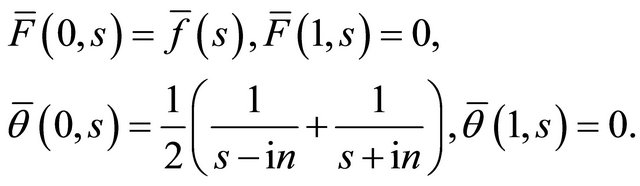 (26)
(26)
Solutions of Equations (23) and (24) subject to the boundary conditions (26) are given by
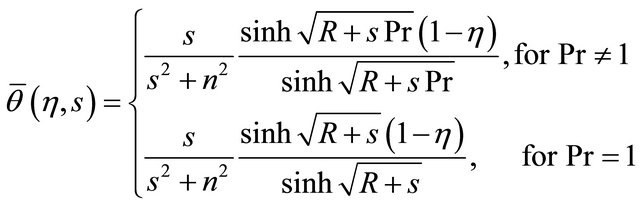 (27)
(27)
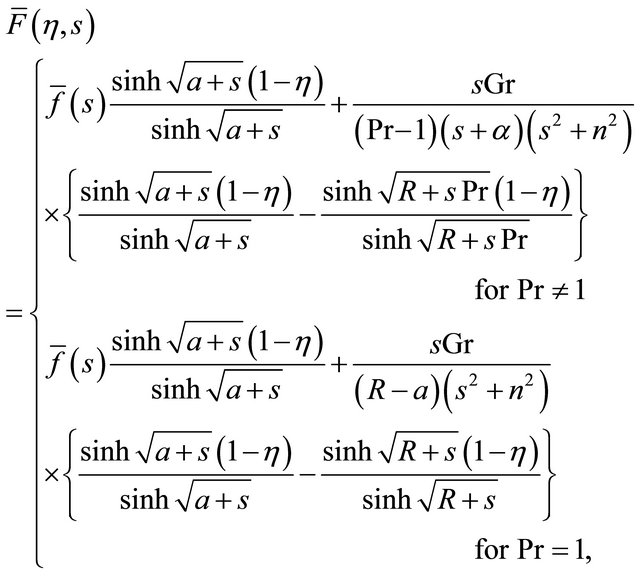 (28)
(28)
Now, we shall considered the following cases.
1) When the wall at  started impulsively:
started impulsively:
In this case , i.e.
, i.e.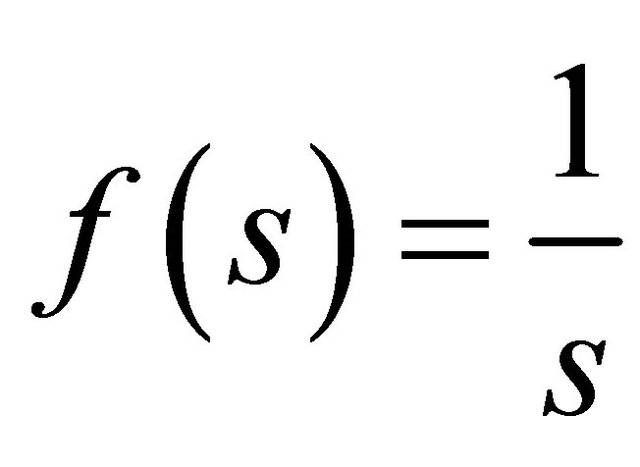 . Then the inverse Laplace transforms of Equations (27) and (28) give the solution for the temperature distribution and the velocity field as
. Then the inverse Laplace transforms of Equations (27) and (28) give the solution for the temperature distribution and the velocity field as
 (29)
(29)
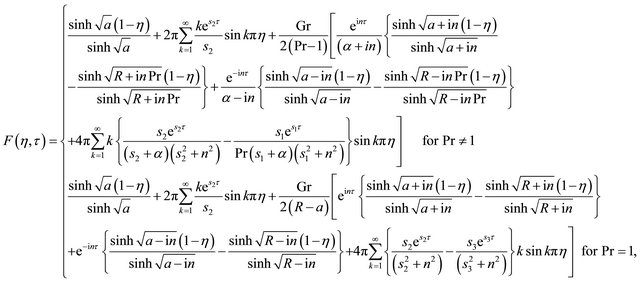 (30)
(30)
where
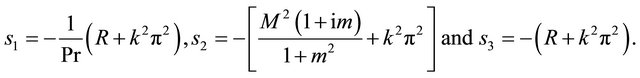 (31)
(31)
2) When the wall at  started acceleratedly:
started acceleratedly:
In this case , i.e.
, i.e.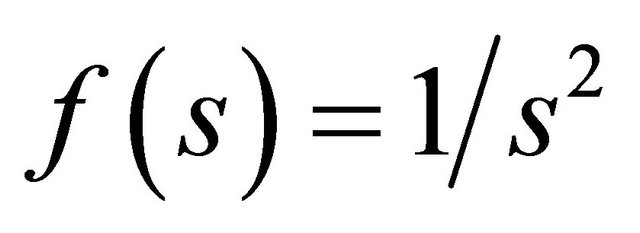 . Then the inverse Laplace transforms of Equations (27) and (28) give the solution for the temperature distribution and the velocity field as
. Then the inverse Laplace transforms of Equations (27) and (28) give the solution for the temperature distribution and the velocity field as
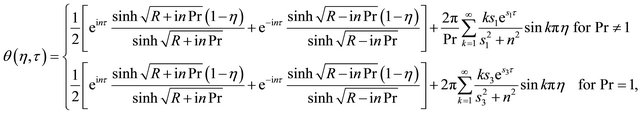 (32)
(32)
 (33)
(33)
where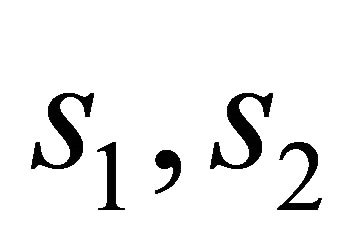 and
and  are given by (31).
are given by (31).
3. Results and Discussion
We have presented the non-dimensional velocity components and temperature distribution for several values of Hall parameter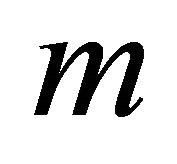 , radiation parameter
, radiation parameter , Prandtl number
, Prandtl number , frequency parameter
, frequency parameter , Grashof number
, Grashof number 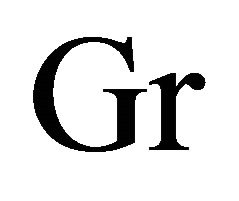 and time
and time  against
against 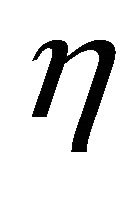 when
when 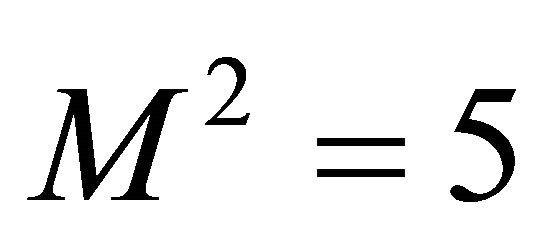 and
and
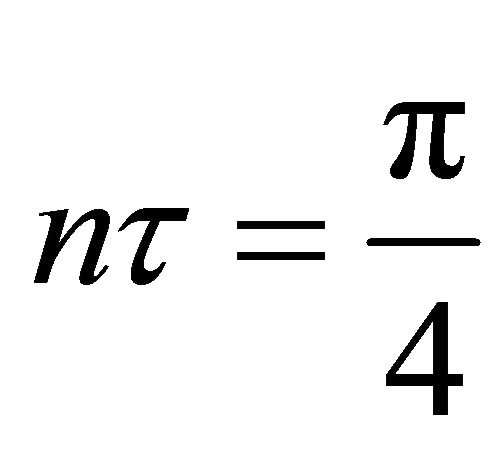 in Figures 2-17. It is seen from Figures 2 and 3 that the primary velocity
in Figures 2-17. It is seen from Figures 2 and 3 that the primary velocity 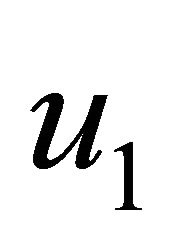 and the magnitude of the secondary velocity
and the magnitude of the secondary velocity 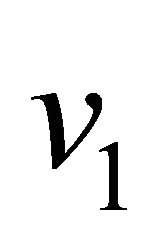 increase with an increase of Hall parameter
increase with an increase of Hall parameter  for the impulsive as well as accelerated motions of one of the channel walls. Figures 4 and 5 show that the primary velocity
for the impulsive as well as accelerated motions of one of the channel walls. Figures 4 and 5 show that the primary velocity 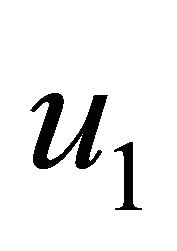 and the magnitude of the secondary velocity
and the magnitude of the secondary velocity 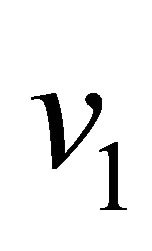 decrease with an increase in radiation parameter
decrease with an increase in radiation parameter 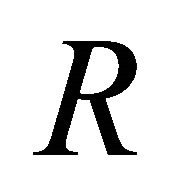 for both the impulsive and accelerated motions of one of the channel
for both the impulsive and accelerated motions of one of the channel
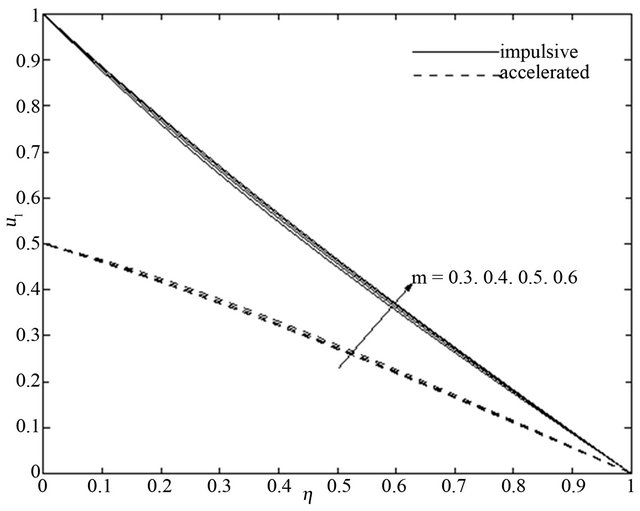
Figure 2. Primary velocity  for different
for different 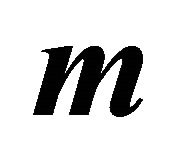 when
when 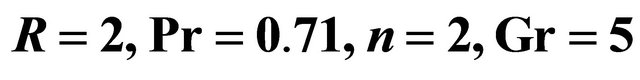 and
and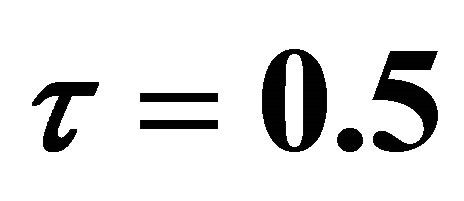 .
.
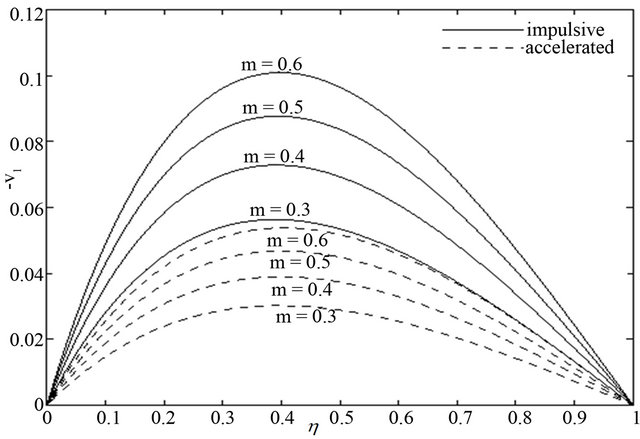
Figure 3. Secondary velocity  for different
for different 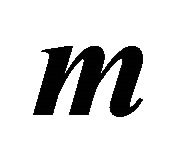 when
when  and
and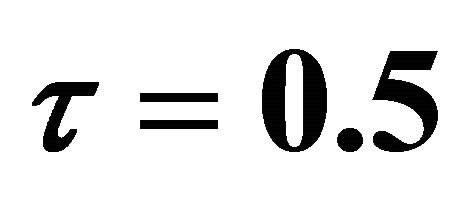 .
.

Figure 4. Primary velocity 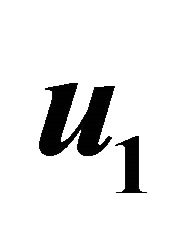 for different
for different  when
when  and
and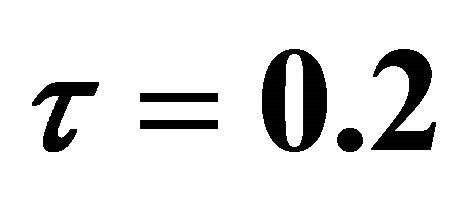 .
.
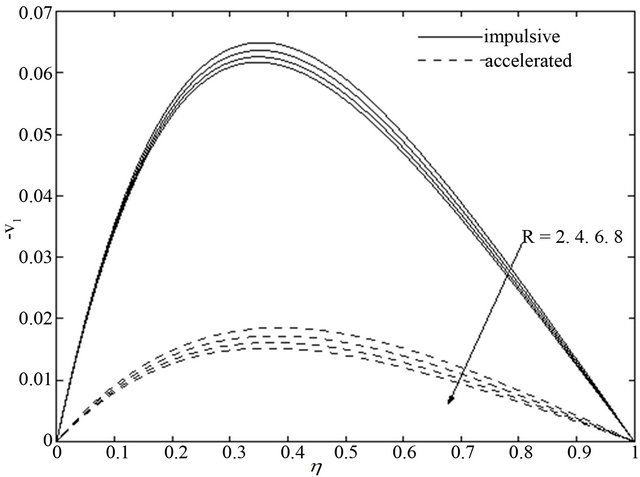
Figure 5. Secondary velocity  for different
for different  when
when 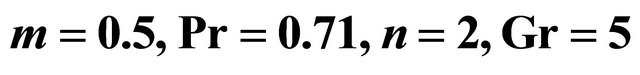 and
and .
.

Figure 6. Primary velocity 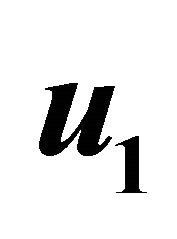 for different
for different  when
when 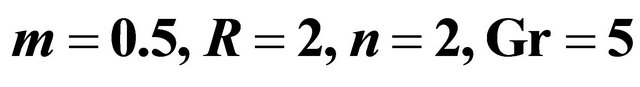 and
and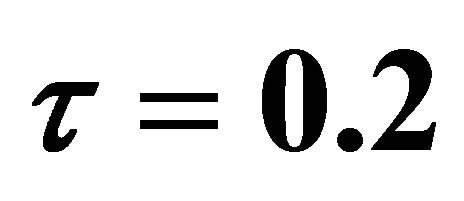 .
.
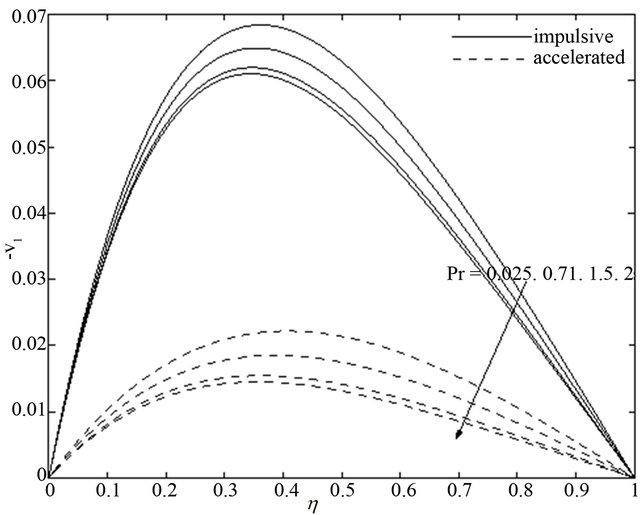
Figure 7. Secondary velocity  for different
for different  when
when  and
and .
.
walls. It is illustrated from Figures 6 and 7 that the primary velocity 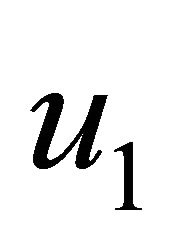 and the magnitude of the secondary velocity
and the magnitude of the secondary velocity  decrease with an increase in Prandtl number
decrease with an increase in Prandtl number 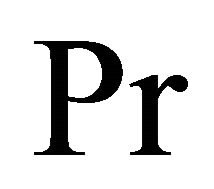 for the impulsive as well as accelerated motions of one of the channel walls. Figures 8 and 9 show that both the primary velocity
for the impulsive as well as accelerated motions of one of the channel walls. Figures 8 and 9 show that both the primary velocity 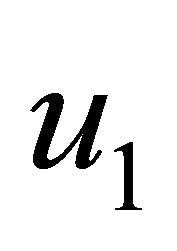 and the magnitude of the secondary velocity
and the magnitude of the secondary velocity 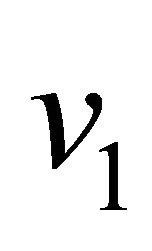 decrease with an increase in frequency parameter
decrease with an increase in frequency parameter  for both the impulsive and accelerated motions of one of the channel walls. An increase in Grashof number
for both the impulsive and accelerated motions of one of the channel walls. An increase in Grashof number 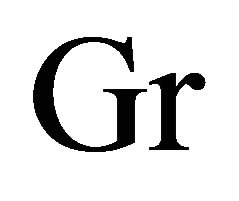 leads to increase the primary velocity
leads to increase the primary velocity 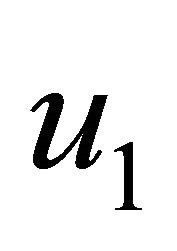 and the magnitude of the secondary velocity
and the magnitude of the secondary velocity 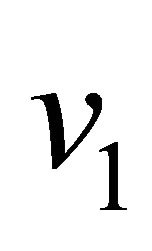 for both the impulsive and accelerated motions of one of the channel walls shown in Figures 10 and 11. It is seen form Figures 12 and 13 that the primary velocity
for both the impulsive and accelerated motions of one of the channel walls shown in Figures 10 and 11. It is seen form Figures 12 and 13 that the primary velocity  and the magnitude of the secondary velocity
and the magnitude of the secondary velocity 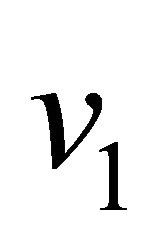 increase with an increase in time
increase with an increase in time  for both the impulsive and accelerated motions of one of the channel walls. It is seen from Figure 14 that the fluid temperature
for both the impulsive and accelerated motions of one of the channel walls. It is seen from Figure 14 that the fluid temperature  decreases with an increase in radiation parameter
decreases with an increase in radiation parameter . This result qualitatively agrees with expectations, since the effect of radiation is to decrease the rate of energy transport to the fluid, thereby decreasing the temperature of the fluid. It is observed from Figure 15 that the fluid temperature
. This result qualitatively agrees with expectations, since the effect of radiation is to decrease the rate of energy transport to the fluid, thereby decreasing the temperature of the fluid. It is observed from Figure 15 that the fluid temperature  increases with an increase in Prandtl number
increases with an increase in Prandtl number . This is in agreement with the physical fact that the thermal boundary layer thickness decreases with increasing
. This is in agreement with the physical fact that the thermal boundary layer thickness decreases with increasing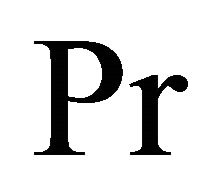 . Figure 16 shows that the fluid temperature
. Figure 16 shows that the fluid temperature  decreases with an increase of frequency parameter
decreases with an increase of frequency parameter . Figure 17 shows that the fluid temperature
. Figure 17 shows that the fluid temperature  increases when time
increases when time  progresses. It is seen from Figures 2-13 that the fluid velocities for the impulsive motion of one of the channel walls is always greater than the accelerated motion.
progresses. It is seen from Figures 2-13 that the fluid velocities for the impulsive motion of one of the channel walls is always greater than the accelerated motion.
The rate of heat transfer at the channel walls 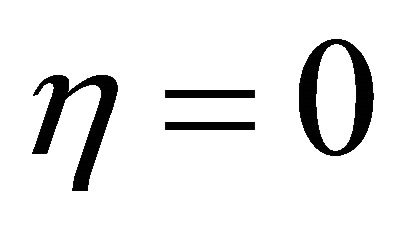 and
and 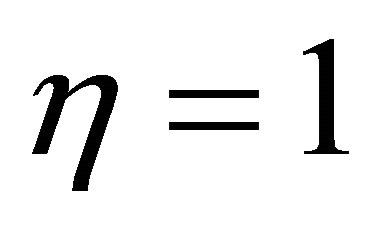 are respectively
are respectively 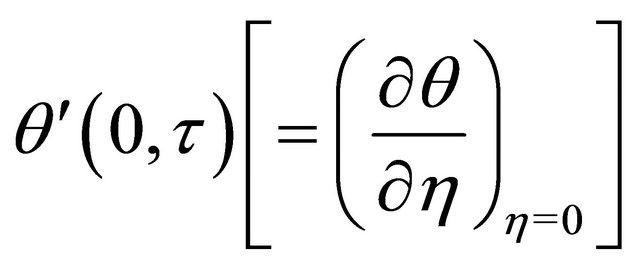 and
and 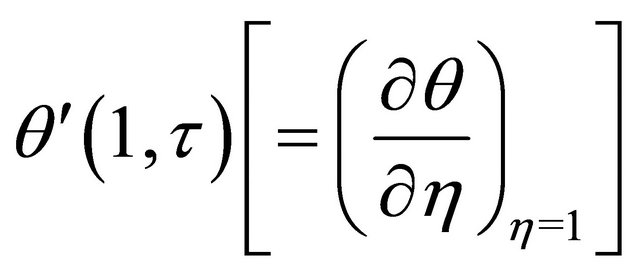 and are given by (see the Equations (34) and (35) below).
and are given by (see the Equations (34) and (35) below).
where 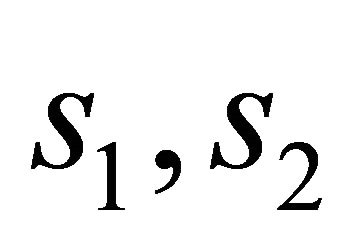 and
and  are given by (31).
are given by (31).
Numerical results of the rate of heat transfer at the channel walls  and
and 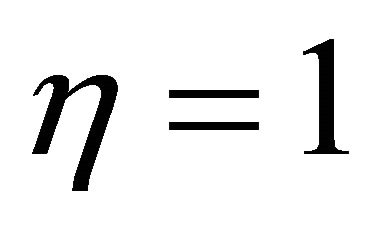 are respectively
are respectively 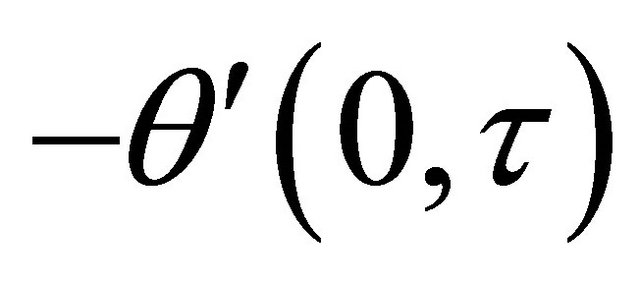 and
and 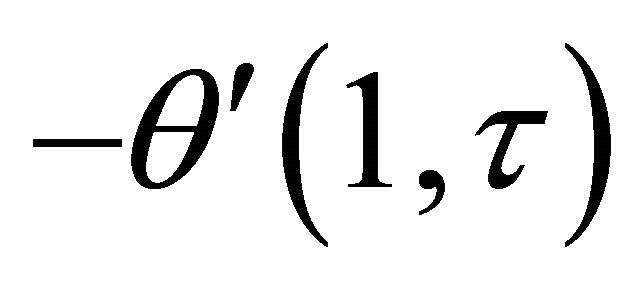 which are presented in Tables 1-3 for several values of Prandtl number
which are presented in Tables 1-3 for several values of Prandtl number , time
, time frequency parameter
frequency parameter 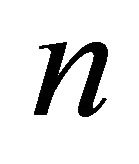 when
when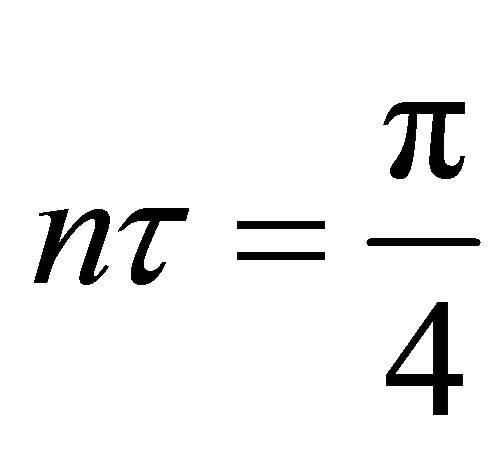 . Table 1 shows that the rate of heat transfer
. Table 1 shows that the rate of heat transfer 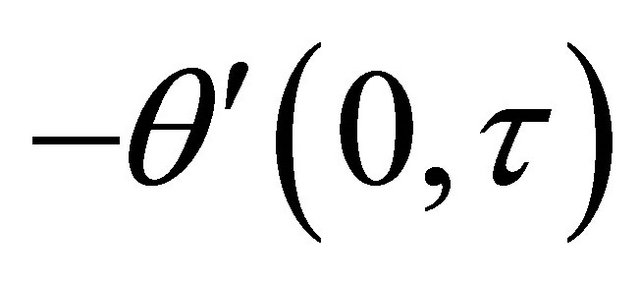 decreases while the rate of heat transfer
decreases while the rate of heat transfer 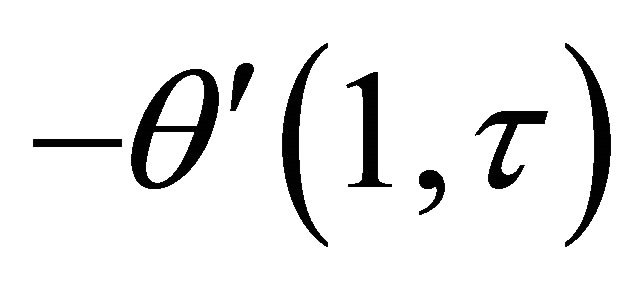 increases with an increase in Prandtl number
increases with an increase in Prandtl number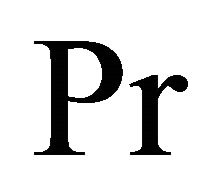 . Table 2 shows that the rate of heat transfer
. Table 2 shows that the rate of heat transfer 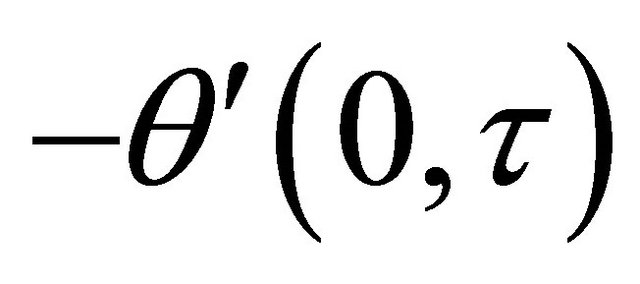 at the wall
at the wall  decreases whereas the rate of heat transfer
decreases whereas the rate of heat transfer 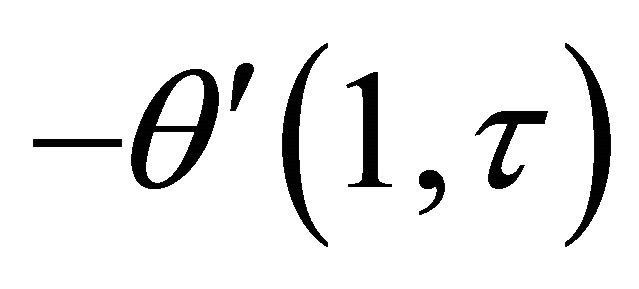 at the wall
at the wall 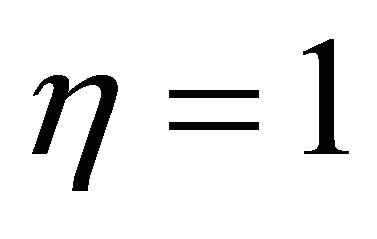 increases when time
increases when time  progresses. It is seen from Table 3 that the rate of heat transfers
progresses. It is seen from Table 3 that the rate of heat transfers 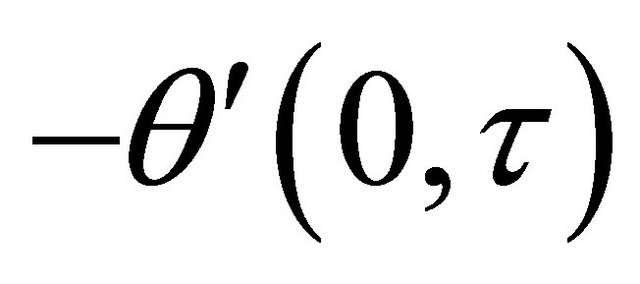 and
and 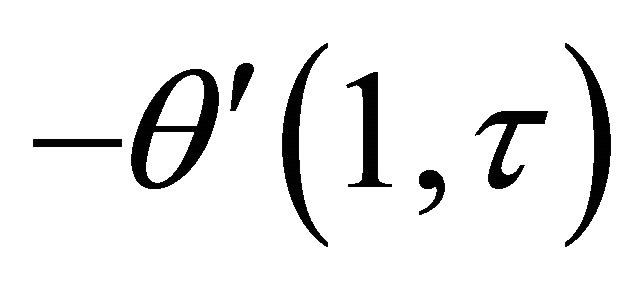 decrease with an increase in frequency parameter
decrease with an increase in frequency parameter .
.
For the impulsive motion, the non-dimensional shear stress at the wall 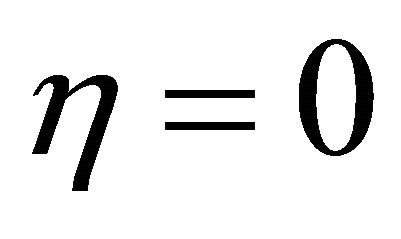 is given by (see the Equations (36) and (37) below).
is given by (see the Equations (36) and (37) below).
|
 (36)
(36)
where 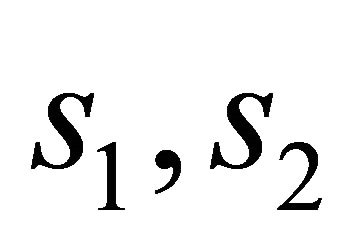 and
and  are given by (31).
are given by (31).
For the accelerated motion, the non-dimensional shear stress at the wall  is as
is as
 (37)
(37)
where 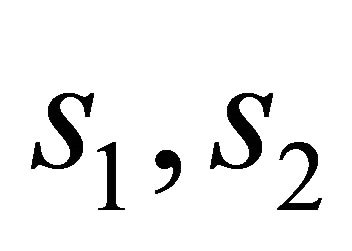 and
and 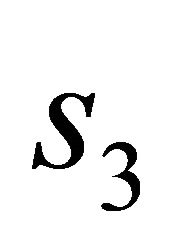 are given by (31).
are given by (31).
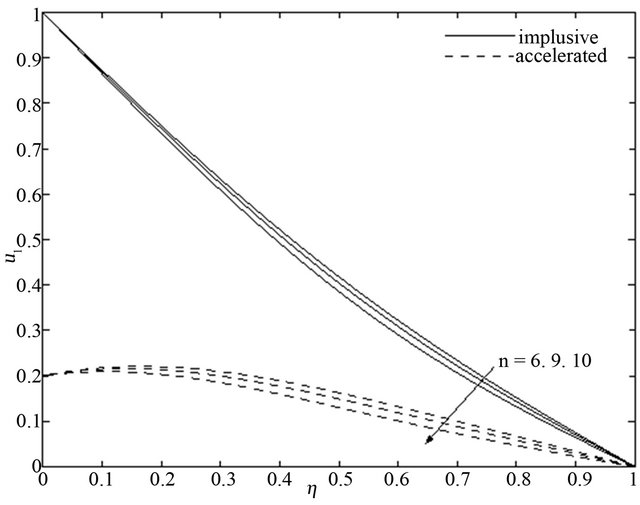
Figure 8. Primary velocity 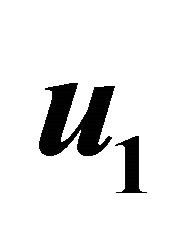 for different
for different  when
when  and
and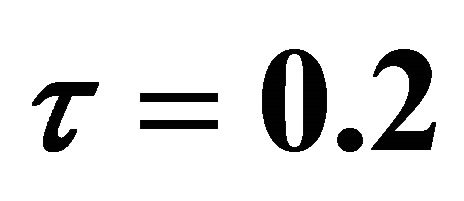 .
.
Figure 9. Secondary velocity  for different
for different 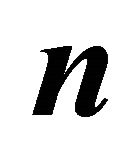 when
when  and
and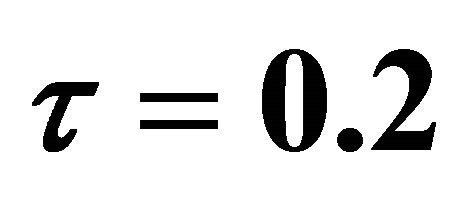 .
.
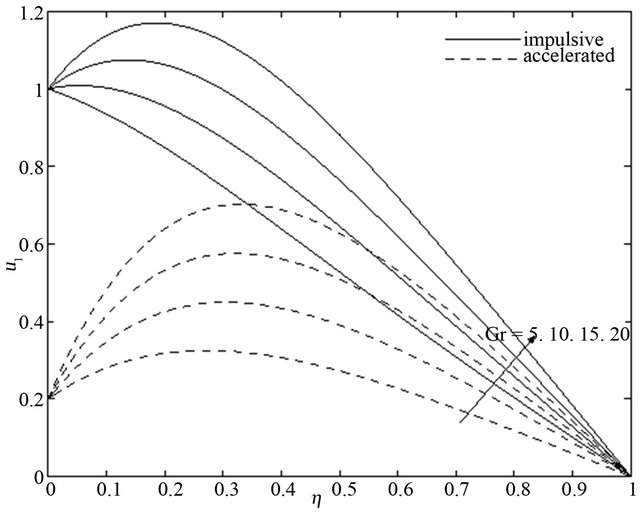
Figure 10. Primary velocity 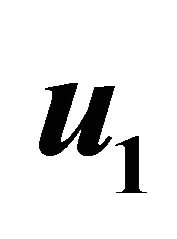 for different
for different  when
when 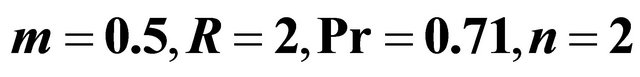 and
and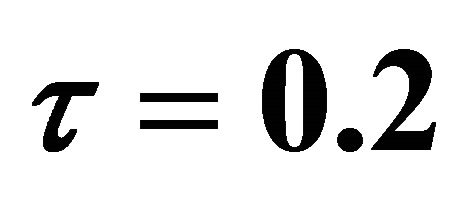 .
.
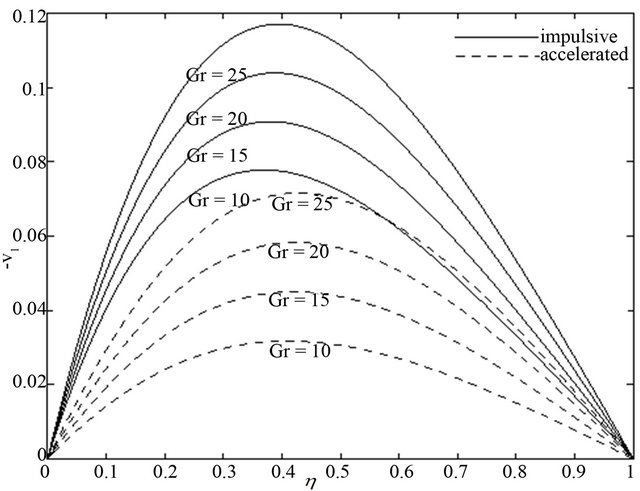
Figure 11. Secondary velocity  for different
for different  when
when 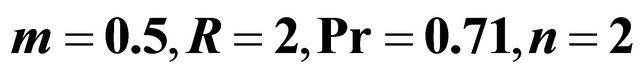 and
and .
.

Figure 12. Primary velocity  for different
for different  when
when 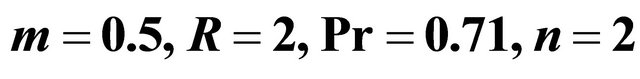 and
and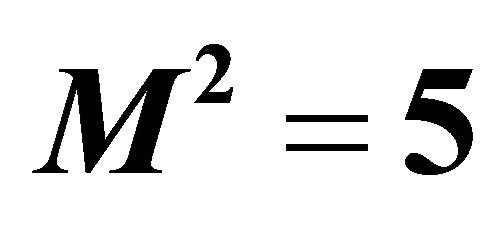 .
.
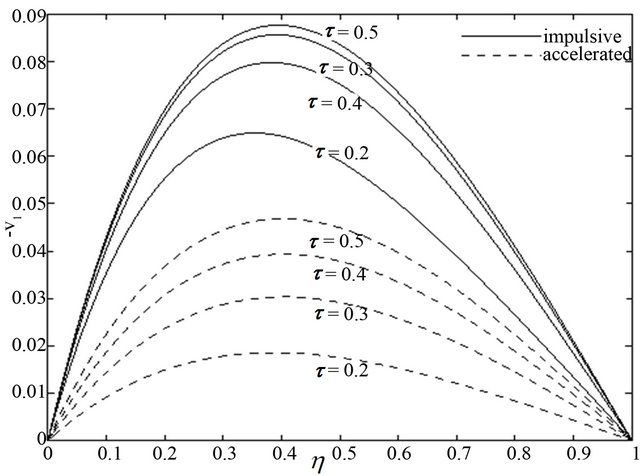
Figure 13. Secondary velocity  for different
for different  when
when  and
and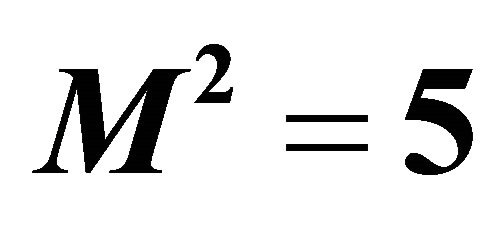 .
.
Table 1. Rate of heat transfer 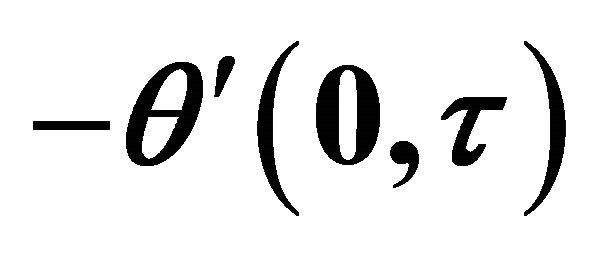 and
and 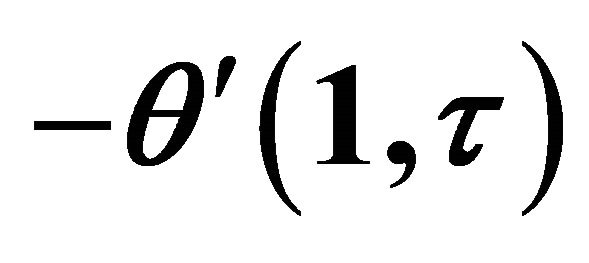 when
when 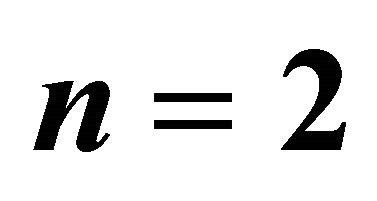 and
and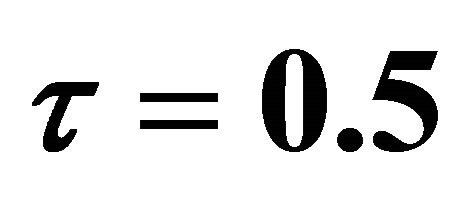 .
.
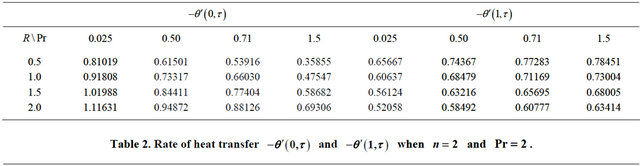
Table 2. Rate of heat transfer 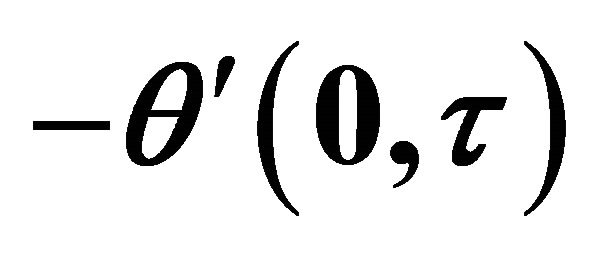 and
and  when
when  and
and .
.

Table 3. Rate of heat transfer 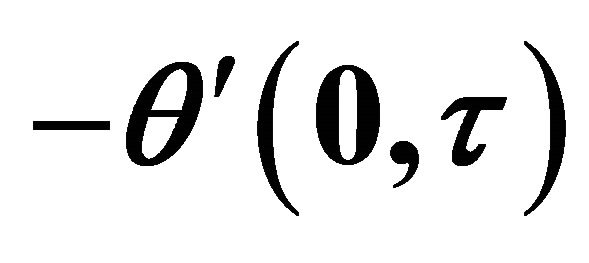 and
and  when
when 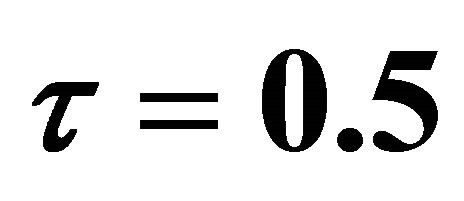 and
and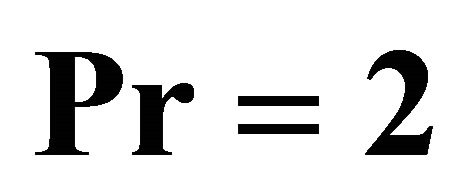 .
.

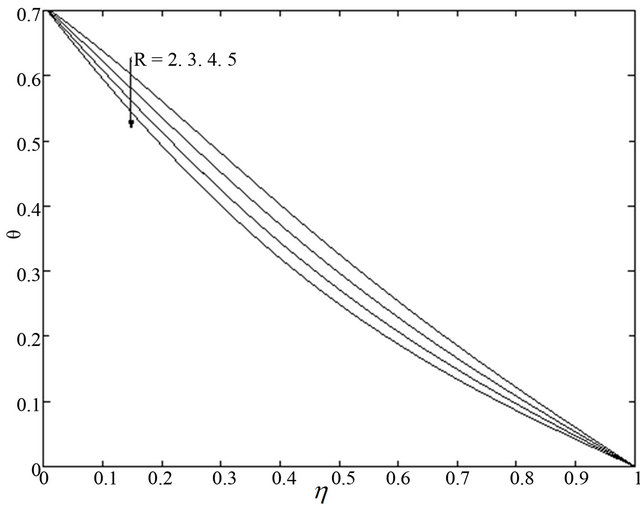
Figure 14. Temperature  for different
for different  when
when 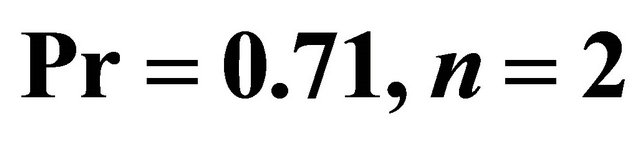 and
and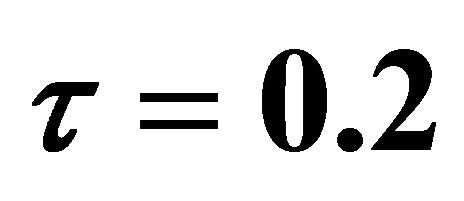 .
.
Numerical results of the non-dimensional shear stresses  and
and  at the wall
at the wall  due to the primary and the secondary flows are plotted in Figures 18-27 against Hall parameter
due to the primary and the secondary flows are plotted in Figures 18-27 against Hall parameter  for several values of radiation parameter
for several values of radiation parameter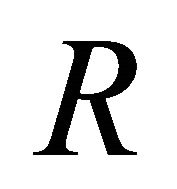 , Prandtl number
, Prandtl number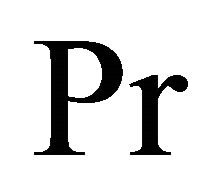 , frequency parameter
, frequency parameter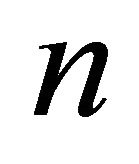 , Grashof number
, Grashof number 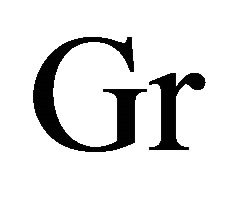 and time
and time  when
when
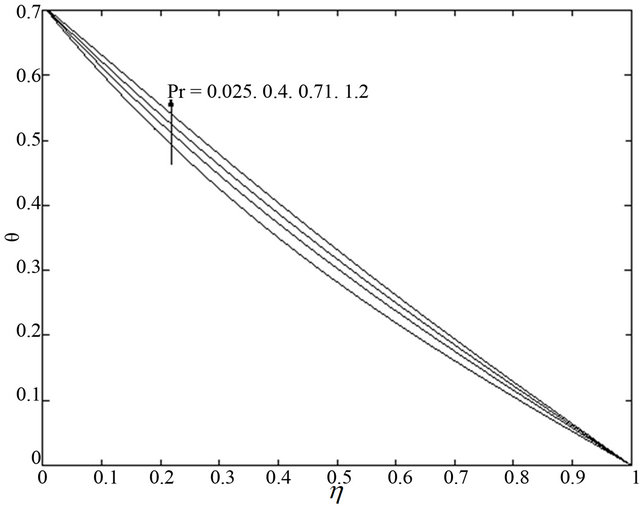
Figure 15. Temperature  for different
for different  when
when 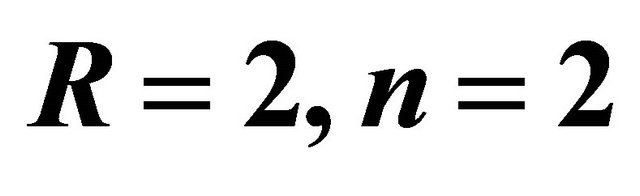 and
and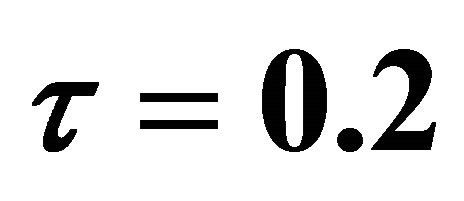 .
.
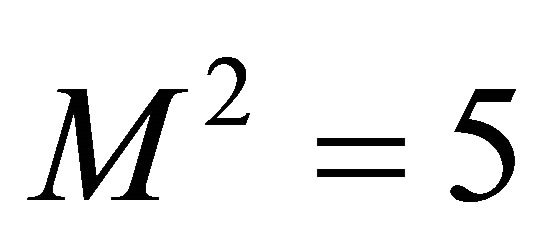 and
and . Figures 18 and 19 show that the shear stress
. Figures 18 and 19 show that the shear stress 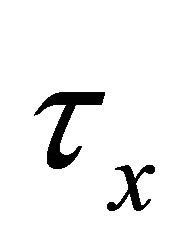 due to the primary flow and the magnitude of the shear stress
due to the primary flow and the magnitude of the shear stress  due to the secondary flow at the wall
due to the secondary flow at the wall 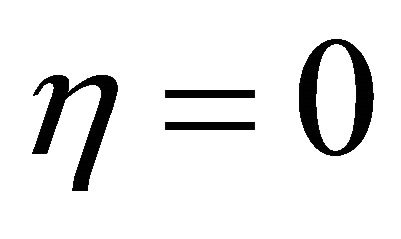 decrease for the impulsive as well as accelerated motions of one of the channel
decrease for the impulsive as well as accelerated motions of one of the channel

Figure 16. Temperature  for different
for different 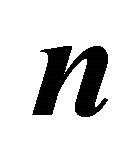 for
for 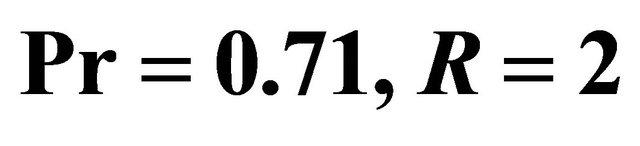 and
and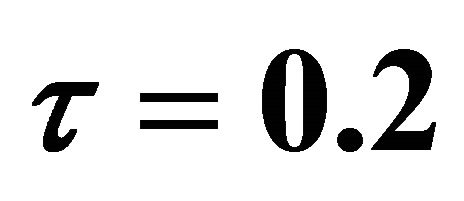 .
.
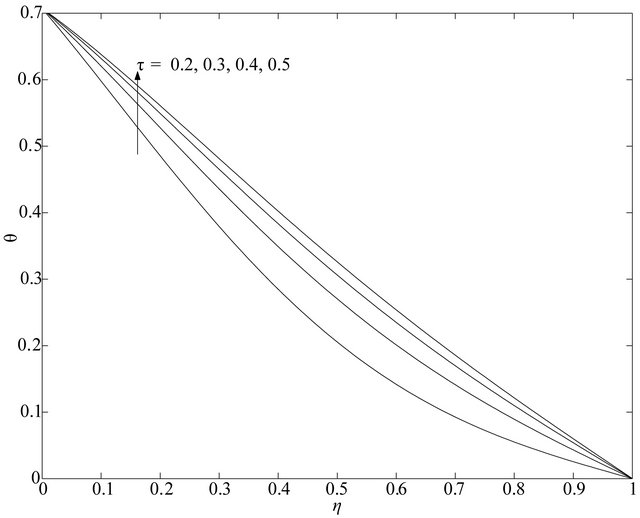
Figure 17. Temperature  for different time
for different time  for
for 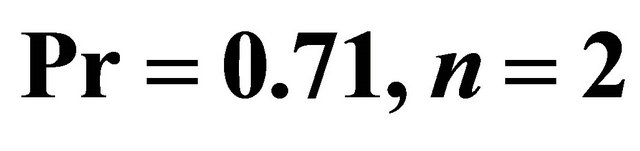 and
and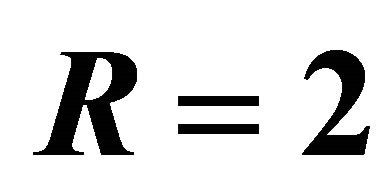 .
.
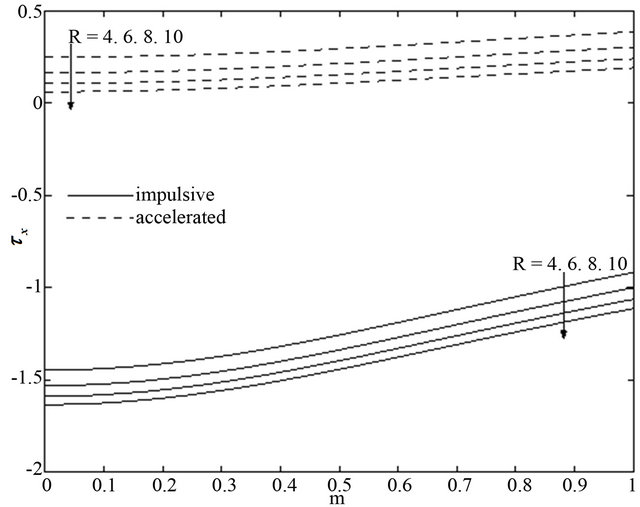
Figure 18. Shear stress  for different
for different  when
when 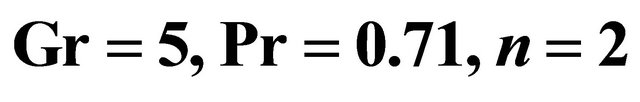 and
and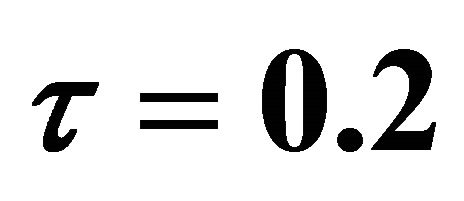 .
.
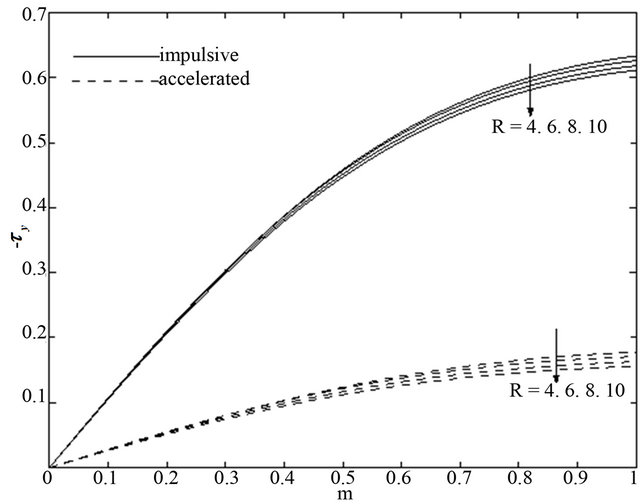
Figure 19. Shear stress  for different
for different  when
when  and
and .
.
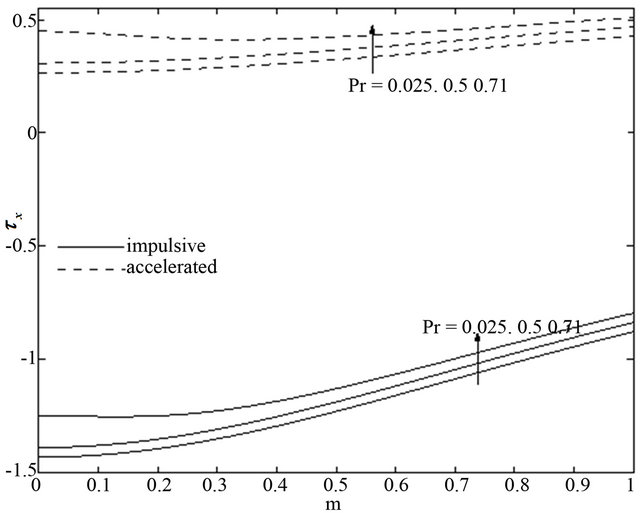
Figure 20. Shear stress 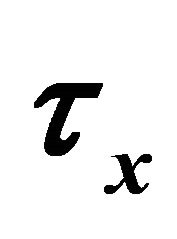 for different
for different  when
when 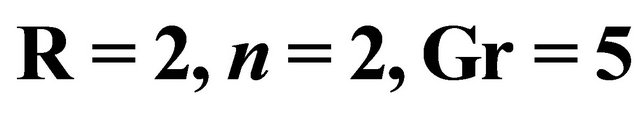 and
and .
.
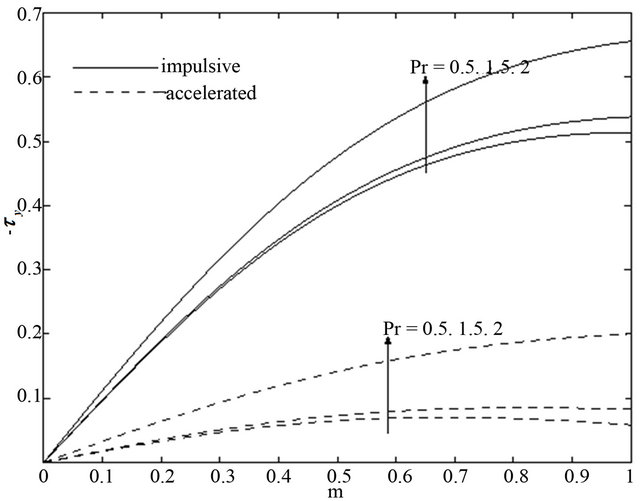
Figure 21. Shear stress  for different
for different  when
when 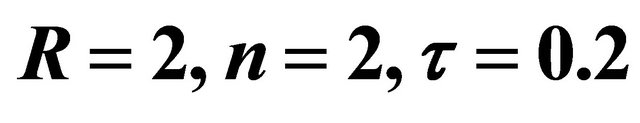 and
and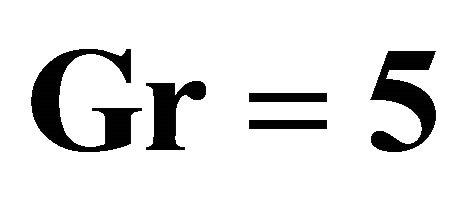 .
.

Figure 22. Shear stress 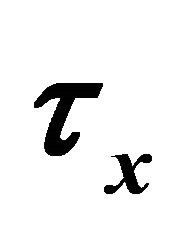 for different
for different 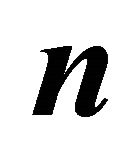 when
when 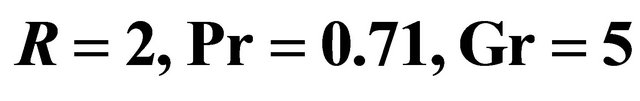 and
and .
.

Figure 23. Shear stress  for different
for different 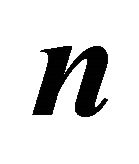 when
when 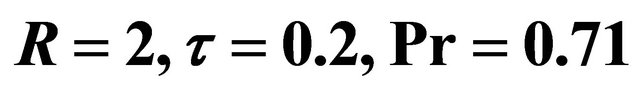 and
and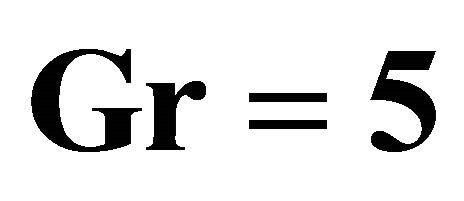 .
.
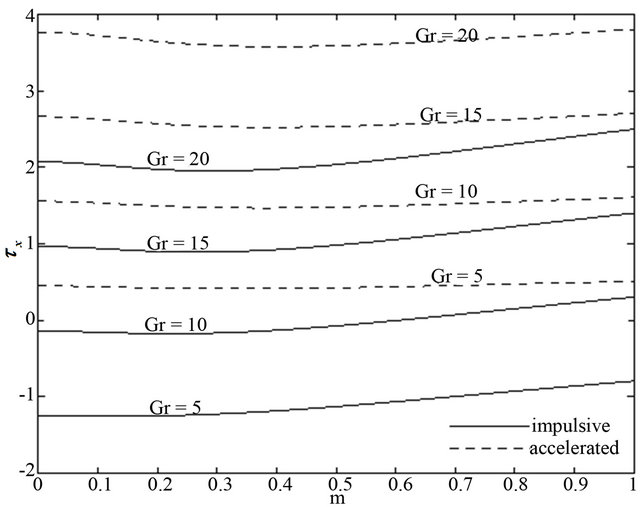
Figure 24. Shear stress  for different
for different  when
when  and
and .
.
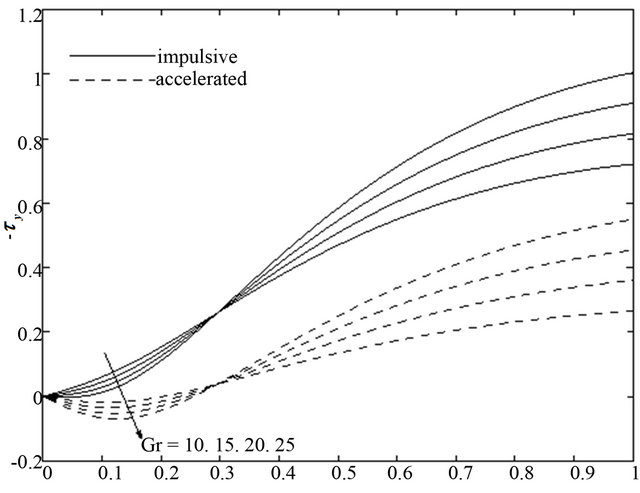
Figure 25. Shear stress  for different
for different  when
when 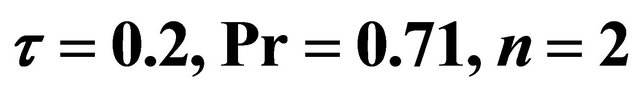 and
and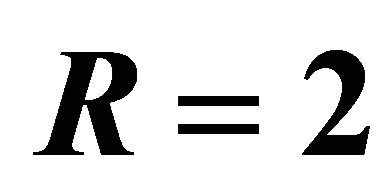 .
.
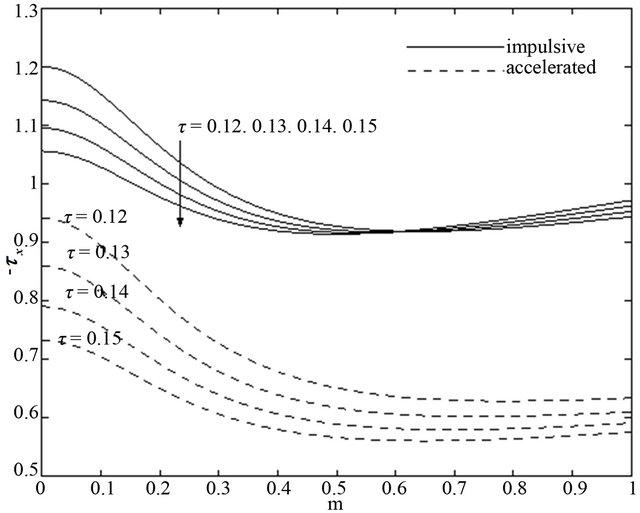
Figure 26. Shear stress 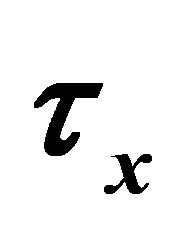 for different time
for different time  when
when 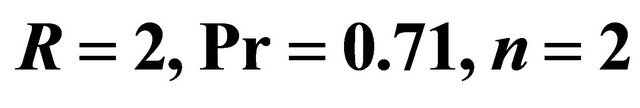 and
and .
.
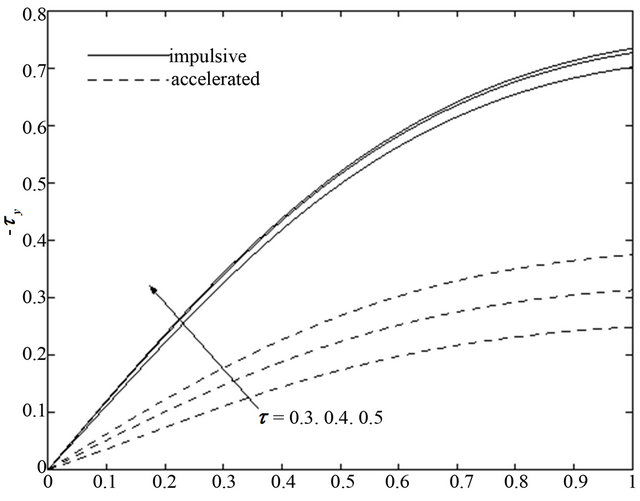
Figure 27. Shear stress  for different time
for different time  when
when  and
and .
.
walls with an increase in radiation parameter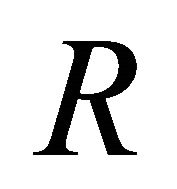 . It is seen from Figures 20 and 21 that for the impulsive and accelerated motions of one of the channel walls the shear stress
. It is seen from Figures 20 and 21 that for the impulsive and accelerated motions of one of the channel walls the shear stress 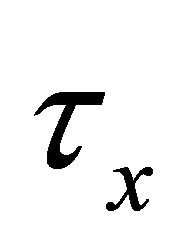 and the magnitude of the shear stress
and the magnitude of the shear stress  increase with an increase of Prandtl number
increase with an increase of Prandtl number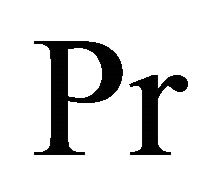 . Figures 22 and 23 show that the shear stress
. Figures 22 and 23 show that the shear stress 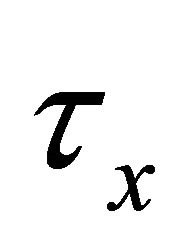 and the magnitude of the shear stress
and the magnitude of the shear stress  decrease with an increase in frequency parameter
decrease with an increase in frequency parameter  for the impulsive as well as accelerated motions of one of the channel walls. An increase of Grashof number
for the impulsive as well as accelerated motions of one of the channel walls. An increase of Grashof number 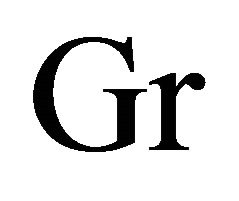 leads to increase in the shear stress
leads to increase in the shear stress  while the magnitude of the shear stress
while the magnitude of the shear stress  decreases for
decreases for  and increases for
and increases for  for both the impulsive and accelerated motions of one of the channel walls show in Figures 24 and 25. Figures 26 and 27 show that for both the impulsive and accelerated motions of one of the channel walls, the magnitude of the share stress
for both the impulsive and accelerated motions of one of the channel walls show in Figures 24 and 25. Figures 26 and 27 show that for both the impulsive and accelerated motions of one of the channel walls, the magnitude of the share stress 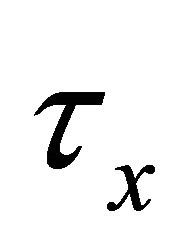 decreases whereas the magnitude of the share stress
decreases whereas the magnitude of the share stress  increases with an increase in time
increases with an increase in time .
.
4. Conclusion
The combined effects of Hall current and radiation on the unsteady MHD free convective flow in a vertical channel with an oscillatory wall temperature have been studied. Radiation has a reterding influence on the fluid velocity components for both the impulsive as well as accelerated motions of one of the channel walls. Hall currents accelerates the fluid velecity components for the impulsive as well as accelerated motions of one of the channel walls. In the prence of radiation the fluid temperature  decreases. Further, the shear stress
decreases. Further, the shear stress 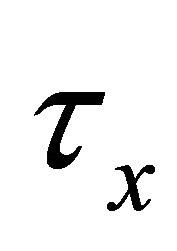 and the absolute value of the shear stress
and the absolute value of the shear stress  at the wall
at the wall 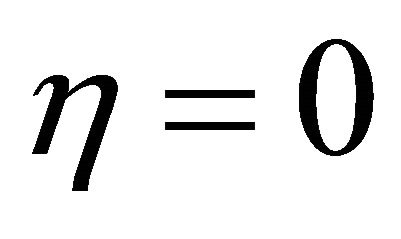 decrease with an increase in radiation parameter
decrease with an increase in radiation parameter  for the impulsive as well as accelerated motions of one of the channel walls. The rate of heat transfers
for the impulsive as well as accelerated motions of one of the channel walls. The rate of heat transfers 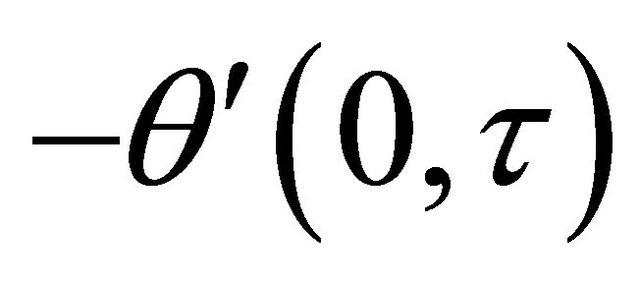 and
and 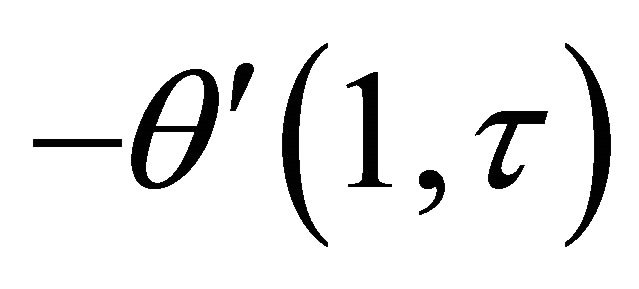 increase with an increase in radiation parameter
increase with an increase in radiation parameter  .
.
REFERENCES
- H. Sato, “The Hall Effects in the Viscous Flow of Ionized Gas between Parallel Plates under Transverse Magnetic Field,” Journal of Physical Society of Japan, Vol. 16, 1961, pp. 14-27. doi:10.1143/JPSJ.16.1427
- O. Miyatake and T. Fujii, “Free Convection Heat Transfer between Vertical Plates—One Plate Isothermally Heated and Other Thermally Insulated,” Heat Transfer—Japanese Research, Vol. 1, 1972, pp. 30-38.
- H. Tanaka, O. Miyatake, T. Fujii and M. Fujii, “Natural Convection Heat Transfer between Vertical Parallel Plates—One Plate with a Uniform Heat Flux and the Other Thermally Insulated,” Heat Transfer—Japanese Research, Vol. 2, 1973, pp. 25-33.
- P. S. Gupta and A. S. Gupta, “Radiation Effect on Hydromantic Convection in a Vertical Channel,” International Journal of Heat Mass Transfer, Vol. 17, No. 12, 1974, pp. 1437-1442. doi:10.1016/0017-9310(74)90053-2
- N. Datta and R. N. Jana, “Hall Effects on Hydromagnetic Convective Flow through a Channel with Conducting Walls,” Internationa Journal of Engineering Science, Vol. 15, No. 9-10, 1977, pp. 561-567. doi:10.1016/0020-7225(77)90052-0
- A. R. Bestman and S. A. Adjepong, “Unsteady Hydromagnetic Free Convection Flow with Radiative Heat Transfer in a Rotating Fluid,” Space Science, Vol. 143, No. 1, 1988, pp. 73-80. doi:10.1007/BF00636756
- H. M. Joshi, “Transient Effects in Natural Convection Cooling of Vertical Parallel Plates,” International Communication Heat and Mass Transfer, Vol. 15, No. 2, 1988, pp. 227-238. doi:10.1016/0735-1933(88)90068-1
- A. K. Singh, “Natural Convection in Unsteady Couette Motion,” Defense Science Journal, Vol. 38, No. 1, 1988, pp. 35-41.
- A. K. Singh, H. K. Gholami and V. M. Soundalgekar, “Transient Free Convection Flow between Two Vertical Parallel Plates,” Heat and Mass Transfer, Vol. 31, No. 5, 1996, pp. 329-331. doi:10.1007/BF02184046
- B. K. Jha, “Natural Convection in Unsteady MHD Couette Flow,” Heat and Mass Transfer, Vol. 37, No. 4-5, 2001, pp. 329-331. doi:10.1007/PL00013295
- M. Narahari, S. Sreenadh and V. M. Soundalgekar, “Transient Free Convection Flow between Long Vertical Parallel Plates with Constant Heat Flux at One Boundary,” Journal of Thermophysics and Aeromechanics, Vol. 9, No. 2, 2002, pp. 287-293.
- B. K. Jha, A. K. Singh and H. S. Takhar, “Transient Free Convection Flow in a Vertical Channel Due to Symmetric Heating,” International Journal of Applied Mechichal Engineering, Vol. 8, No. 3, 2003, pp. 497-502.
- A. K. Singh and T. Paul, “Transient Natural Convection between Two Vertical Walls Heated/Cooled Asymetrically,” International Journal of Applied Mechanical Engineering, Vol. 11, No. 1, 2006, pp. 143-154.
- D. C. Sanyal and A. Adhikari, “Effects of Radiation on MHD Vertical Channel Flow,” Bulletin of Calcutta Mathematical Society, Vol. 98, No. 5, 2006, pp. 487-497.
- P. Mebine, “Radiation Effects on MHD Couette Flow with Heat Transfer between Two Parallel Plates,” Global Journal of Pure and Applied Mathematics, Vol. 3, No. 2, 2007, pp. 1-12.
- T. Grosan and I. Pop, “Thermal Radiation Effect on Fully Developed Mixed Convection Flow in a Vertical Channel,” Technische Mechanik, Vol. 27, No. 1, 2007, pp. 37- 47.
- M. Guria and R. N. Jana, “Hall Effects on the Hydromagnetic Convective Flow through a Rotating Channel under General Wall Conditions,” Magnetohydrodynamics, Vol. 43, No. 3, 2007, pp. 287-300.
- B. K. Jha and A. O. Ajibade, “Unsteady Free Convective Couette Flow Of Heat Generating/Absorbing Fluid,” International Journal of Energy and Technology, Vol. 2, No. 12, 2010, pp. 1-9.
- M. Narahari, “Effects of Thermal Radiation and Free Convection Currents on the Unsteady Couette Flow between Two Vertical Parallel Plates with Constant Heat Flux at One Boundary,” WSEAS Transactions on Heat and Mass Transfer, Vol. 5, No. 1, 2010, pp. 21-30.
- U. S. Rajput and P. K. Sahu, “Transient Free Convection MHD Flow between Two Long Vertical Parallel Plates with Constant Temperature and Variable Mass Diffusion,” International Journal of Mathematical Analysis, Vol. 5, No. 34, 2011, pp. 1665-6671.
- S. Das, B. C. Sarkar and R. N. Jana, “Radiation Effects on Free Convection MHD Couette Flow Started Exponentially with Variable Wall Temperature in Presence of Heat Generation,” Open Journal of Fluid Dynamics, Vol. 2, No. 1, 2007, pp. 14-27.
- C. Mandal, S. Das and R. N. Jana, “Effect of Radiation on Transient Natural Convection Flow between Two Vertical Walls,” International Journal of Applied Information Systems, Vol. 2, No. 2, 2012, pp. 49-56.
- S. Das, S. K. Guchhait and R. N. Jana, “Radiation Effects on Unsteady MHD Free Convective Couette Flow of Heat Generation/Absorbing Fluid,” International Journal of Computer Applications, Vol. 39, No. 3, 2012, pp. 42- 51.
- B. C. Sarkar, S. Das and R. N. Jana, “Effects of Radiation on MHD Free Convective Couette Flow in a Rotating System,” International Journal of Engineering Research and Application, Vol. 2, No. 4, 2012, pp. 2346-2359.
- B. C. Sarkar, S. Das and R. N. Jana, “Oscillatory MHD Free Convective Flow between Two Vertical Walls in a Rotating System,” Advance in Applied Science Research, Vol. 3, No. 5, 2012, pp. 3311-3325.
- A. C. Cogley, W. C. Vincentine and S. E. Gilles, “A Differential Approximation for Radiative Transfer in a NonGray Gas Near Equilibrium,” American Institute of Aeronautics and Astronautics Journal, Vol. 6, No. 3, 1968, pp. 551- 555.
- T. G. Cowling, “Magnetohydrodynamics,” Interscience, New York, 1957.



