Open Journal of Fluid Dynamics
Vol.2 No.4(2012), Article ID:25497,4 pages DOI:10.4236/ojfd.2012.24012
Effects of Thermophoresis on Unsteady MHD Free Convective Heat and Mass Transfer along an Inclined Porous Plate with Heat Generation in Presence of Magnetic Field
1Department of Natural Sciences, Daffodil International University, Dhaka, Bangladesh
2Department of Mathematics, Comilla University, Comilla, Bangladesh
Email: akabir@daffodilvarsity.edu.bd
Received September 24, 2012; revised October 25, 2012; accepted November 14, 2012
Keywords: Heat Generation; Magnetic Field; Nusselt Number; Stanton Number; Thermophoresis
ABSTRACT
An analysis of Thermophoresis effect on unsteady magneto-hydrodynamic free convection flow over an inclined porous plate with time dependent suction in presence of magnetic field with heat generation has been considered by employing Nachtsheim-Swigert shooting iteration technique along with sixth order Runge-Kutta integration scheme. Resulting non-dimensional velocity, temperature and concentration profiles are then presented graphically for different values of the parameters entering into the problem. Finally, the effects of the pertinent parameters on the skin-friction coefficient, the rate of heat transfer (Nusselt number) and wall deposition flux (Stanton number), which are of physical interest, are exhibited in tabular form.
1. Introduction
The free convection processes involving the combined mechanism of heat and mass transfer are encountered in many natural processes, in many industrial applications and in many chemical processing systems. The study of free convective mass transfer flow has become the object of extensive research as the effects of heat transfer along with mass transfer effects are dominant features in many engineering applications such as rocket nozzles, cooling of nuclear reactors, high sinks in turbine blades, high speed aircrafts and their atmospheric re-entry, chemical devices and process equipments.
S. Ostrach [1], the initiator of the study of convection flow, made a technical note on the similarity solution of transient free convection flow past a semi infinite vertical plate by an integral method. B. C. Sakiadis [2] analyzed the boundary layer flow over a solid surface moving with a constant velocity. This boundary layer flow situation is quite different from the classical Blasius problem of boundary flow over a semi-infinite flat plate due to entrainment of ambient fluid. L. E. Erickson, L. T. Fan and V. G. Fox [3] extended the work of Sakiadis for suction or injection of a smooth surface. S. L. Goren [4] studied thermophoresis in laminar flow over a horizontal flat plate. He found the deposition of particles on cold plate and particles free layer thickness in hot plate case. E. M. Sparrow [5] explained a parameter named Rosseland approximation to describe the radiation heat flux in the energy equation in his book. R. S. R. Gorla [6] depicted the application of linearly stretched surface in electrochemistry. G. M. Homsy, F. T. Geyling and K. L. Walker [7] solved Blasius series solution. A. Raptis and C. Perdikis [8] studied numerically free convection flow through a porous medium bounded by a semi-infinite vertical porous plate. M. Epstein, G. M. Hauser and R. E. Henry [9] analyzed the thermophoresis in natural convection for a cold vertical surface. M. A. Alabraba, A. R. Bestman and A. Ogulu [10] studied the interaction of mixed convection with thermal radiation in laminar boundary layer flow taking into account the binary chemical reaction and Soret-Dufour effects. A. Sattar and M. Hossain [11] investigated the unsteady free convective flow, with Hall currents and mass transfer, past an accelerated vertical porous plate in the presence of a transverse magnetic field while assuming the plate temperature and concentration to be functions of time. M. A. Hossain and H. S. Takhar [12] analyzed the effect of radiation using the Rosseland diffusion approximation that leads to non similar boundary layer equation governing the mixed convection flow of an optically dense viscous incompressible fluid past heated vertical plate with a free uniform stream velocity and surface temperature.
In recent years, it is found that the thermophoresis phenomenon has many practical applications in removing small particles from gas streams, in determining exhaust gas particle trajectories from combustion devices, and in studying the particulate material deposition on turbine blades. It has been found that thermophoresis is the dominant mass transfer mechanism in the modified chemical vapor deposition (MCVD) process as currently used in the fabrication of optical fiber performs. Thermophoretic deposition of radioactive particles is considered to be one of the important factors causing accidents in nuclear reactors. J.-S. Lin, C.-J. Tsai and C.-P. Chang [13] investigated the suppression of particle deposition from flow through a tube with circular cross-section when the wall temperature exceeds that of the gas. M. A. Seddek [14] investigated finite element method for the effects of thermophoresis and chemical reaction on a boundary layer hydro magnetic flow with heat and mass transfer over a heat surface and found that the velocity, temperature and concentration profiles reduce with the increase of thermophoretic parameter. M. S. Alam, M. M. Rahman and M. A. Sattar [15] considered the effects of heat generation and thermophoresis on steady, laminar, hydromagnetic, two-dimensional flow with heat and mass transfer along a semi-infinite, permeable inclined flat surface. M. A. Samad and M. E. Karim [16] considered an unsteady two dimensional MHD flow of a viscous incompressible and electrically conducting fluid along a vertical plate with time dependent suction under the influence of a uniform magnetic field. M. A. A. Mahmoud [17] made a report on the effects of thermal radiation and variable viscosity on the unsteady hydromagnetic flow of an electrically conducting fluid past an infinite vertical porous plate in the presence of viscous dissipation and time dependent suction. M. A. Samad, M. E. Karim and D. Mohammad [18] calculated numerically the effect of thermal radiation on steady MHD free convectoin flow taking into account the Rosseland diffusion approximaion. P. Loganathan and P. P. Arasu [19] analyzed the effects of thermophoresis particle deposition on non-Darcy MHD mixed convective heat and mass transfer past a porous wedge in the presence of suction or injection. M. Ferdows, Nazmul and M. OTA [20] descried that in the presence of uniform magnetic field with viscous dissipation at the wall, the thermophoretic parameter is one of the most useful parameter to control the boundary layer of the fluid. O. D. Makinde and P. O. Olanrewaju [21] investigated unsteady mixed convection with the thermo-diffusion and diffusion-thermal effects past a vertical porous plate moving through a binary mixture in the presence of radiative heat transfer and n-th order Arrhenius-type chemical reaction. N. Ghara, S. L. Maji, S. Das, R. Jana and S. K. Ghosh [22] analyzed the unsteady MHD Couette flow of a viscous fluid between two infinite non-conducting horizontal porous plates with the consideration of both Hall currents and ion-slip.
The present paper is the investigation of the thermophoretic effects of an electrically conducting viscous incompressible fluid interaction with heat generation on the flow over an inclined porous plate in the presence of heat and mass transfer permitted by a transversely applied uniform magnetic field taking into account the Rosseland diffusion approximation. The investigation is based on known similarity analysis and the local similarity solutions are obtained numerically.
2. Mathematical Analysis
In this work we considered an unsteady two-dimensional MHD flow of a viscous incompressible and electrically conducting fluid past an inclined porous plate with an angle 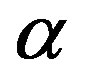 to the vertical embedded in a porous medium under the influence of a uniform magnetic field. Initially the flow is assumed to be in the x-direction, which is chosen along the plate in the upward direction and y-axis normal to it. The plate and the fluid are at a constant temperature T¥ in a stationary condition with concentration level C¥ at all points. At time t > 0 the plate is assumed to be moving in the upward direction with the velocity
to the vertical embedded in a porous medium under the influence of a uniform magnetic field. Initially the flow is assumed to be in the x-direction, which is chosen along the plate in the upward direction and y-axis normal to it. The plate and the fluid are at a constant temperature T¥ in a stationary condition with concentration level C¥ at all points. At time t > 0 the plate is assumed to be moving in the upward direction with the velocity 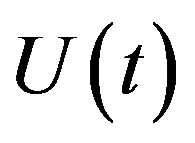 and there is a suction velocity
and there is a suction velocity 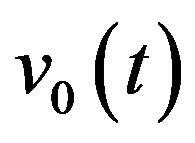 taken to be a function of time, the temperature of the plate raised to
taken to be a function of time, the temperature of the plate raised to 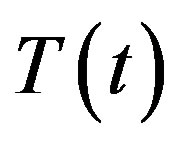 and the concentration level at the plate is raised to
and the concentration level at the plate is raised to 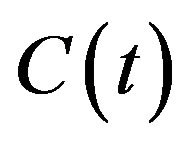 where
where 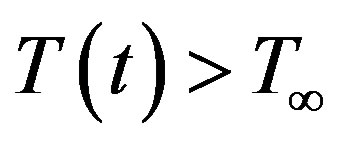 and
and 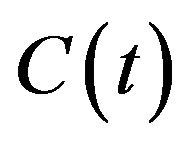 > C¥. The plate is considered to be of infinite length, all derivatives with respect to x vanish and so the physical variables are functions of y and t only. The flow configuration and the coordinate system are shown in the Figure 1.
> C¥. The plate is considered to be of infinite length, all derivatives with respect to x vanish and so the physical variables are functions of y and t only. The flow configuration and the coordinate system are shown in the Figure 1.
The fluid is assumed to have constant properties except that the influence of the density variations with temperature and concentration, which are considered only in the body force term, and is considered to be gray, absorbing emitting radiation but non-scattering medium, and the Rosseland approximation is used to describe the radioactive heat flux in the energy equation. A uniform magnetic field of strength B0 is applied normal to the plate parallel to y-direction.
Under the usual boundary layer and Boussinesq approximation and using the Darcy-Forchhemier model, the flow and heat transfer in the presence of radiation are governed by the following equations.
Continuity Equation
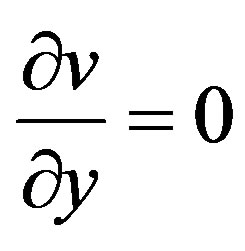 (1)
(1)
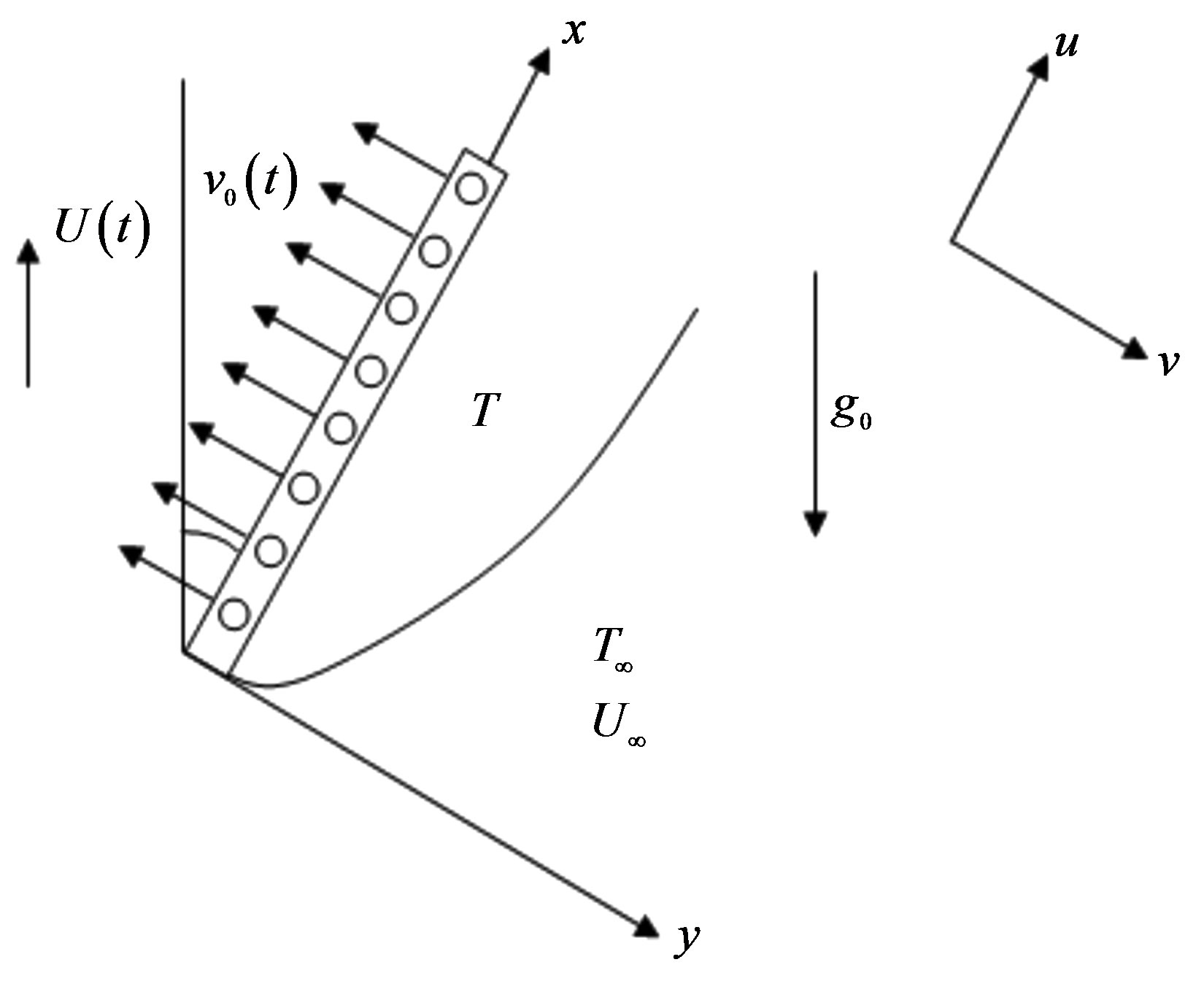
Figure 1. Flow configuration and coordinate system.
Momentum Equation
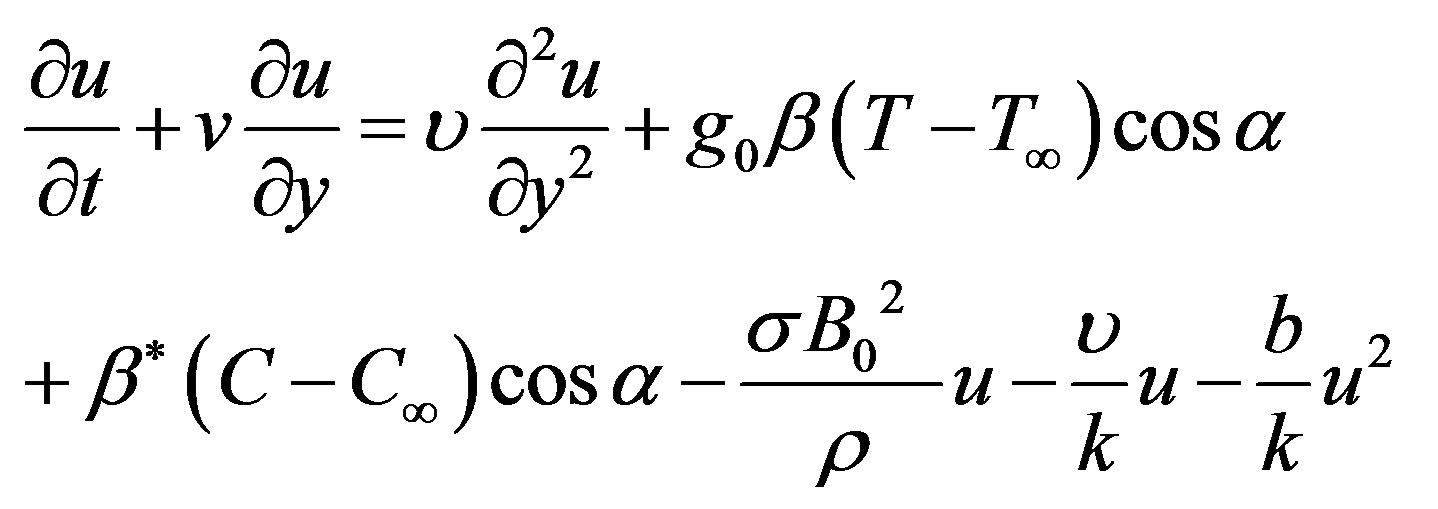 (2)
(2)
Energy Equation
 (3)
(3)
Concentration Equation
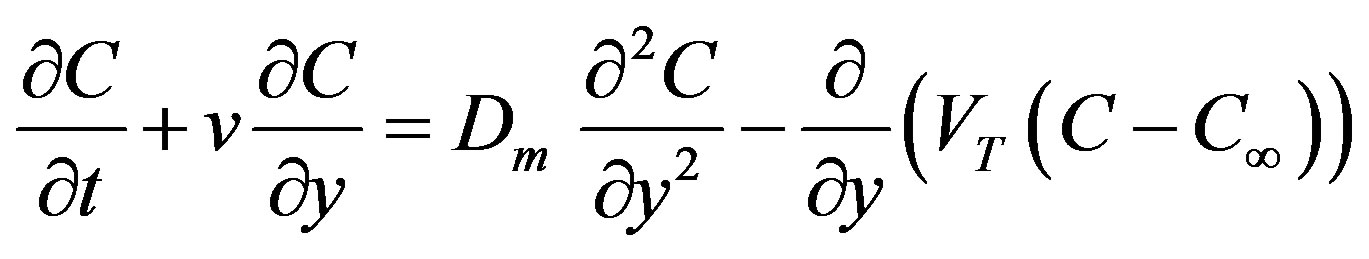 (4)
(4)
where u and v are the velocity components along xand y-directions respectively, υ is the kinematic viscosity, ρ is the density of the fluid, g0 is the acceleration due to gravity, β is the coefficient of volume expansion, β* is the volumetric coefficient of expansion with concentration, α is the inclination of the plate, σ is the electric conductivity, B0 is the uniform magnetic field strength (magnetic induction), k is the Darcy permeability, b is the empirical constant, cp is the specific heat at constant pressure, T and T∞ are the fluid temperature within the boundary layer and in the free-stream respectively, while C and C∞ are the corresponding concentrations. Also Q0 is the heat generation, Dm is the coefficient of mass diffusivity and VT is the thermophoretic velocity.
The effects of thermophoresis are being taken into account to help in the understanding of the mass deposition variation on the surface. We further assume that 1) the mass flux of particles is sufficiently small so that the main stream velocity and temperature fields are not affected by the thermo-physical processes experienced by the relatively small number of particles; 2) due to the boundary layer behavior the temperature gradient in the y-direction is much larger than that in the x-direction and hence only the thermophoretic velocity component which is normal to the surface is of importance; 3) the fluid has constant kinematic viscosity and thermal diffusivity, and that the Boussinesq approximation may be adopted for unsteady laminar flow; 4) the particle diffusivity is assumed to be constant, and the concentration of particles is sufficiently dilute to assume that particle coagulation in the boundary layer is negligible; and 5) the magnetic Reynolds number is assumed to be small so that the induced magnetic field is negligible in comparison to the applied magnetic field.
Initially (t = 0) the fluid and the plate are at rest. Thus the no slip boundary conditions at the surface of the plate for the above problem for t > 0 are:
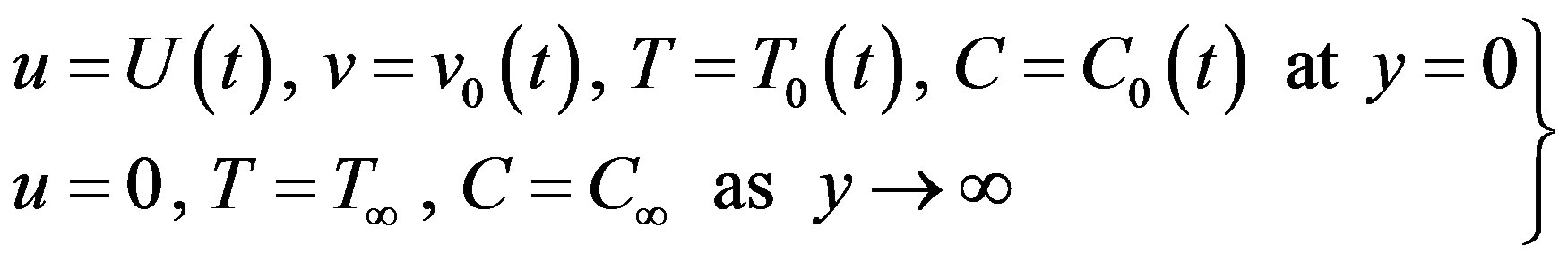 (5)
(5)
The effect of thermophoresis is usually prescribed by means of an average velocity that a particle will acquire when exposed to a temperature gradient. For boundary layer analysis it is found that the temperature gradient along the plate is much lower than the temperature gradient normal to the surface, i.e., . So the component of thermophoretic velocity along the plate is negligible compared to the component of its normal to the surface. As a result, the thermophoretic velocity VT which appears in Equation (4) can be written as
. So the component of thermophoretic velocity along the plate is negligible compared to the component of its normal to the surface. As a result, the thermophoretic velocity VT which appears in Equation (4) can be written as
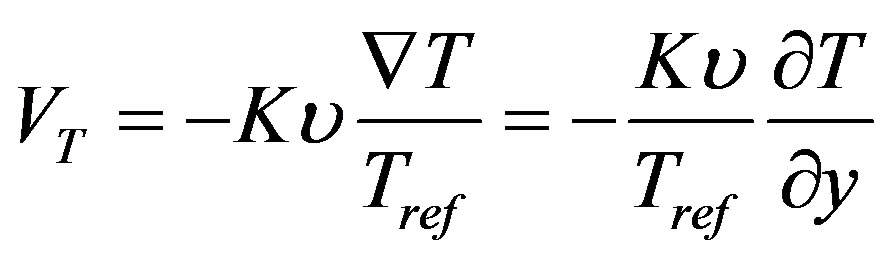 , (6)
, (6)
where K is the thermophoretic coefficient which ranges in value from 0.2 to 1.2 as indicated by G. K. Batchelor and C. Shen [23] and is defined from the theory of L. Talbot, R. K. Cheng, A. W. Schefer and D. R. Wills [24] by:
 , (7)
, (7)
where C1, C2, C3, Cm, Cs and Ct are constants,  and
and  are the thermal conductivities of the fluid and diffused particles, respectively and Kn is the Knudsen number.
are the thermal conductivities of the fluid and diffused particles, respectively and Kn is the Knudsen number.
A thermophoretic parameter 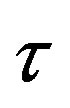 can be defined (see A. F. Mills, X. Hang and F. Ayazi [25] and R. Tsai [26] as follows:
can be defined (see A. F. Mills, X. Hang and F. Ayazi [25] and R. Tsai [26] as follows:
 . (8)
. (8)
Typical values of 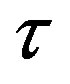 are 0.01, 0.1 and 1.0 corresponding to approximate values of
are 0.01, 0.1 and 1.0 corresponding to approximate values of 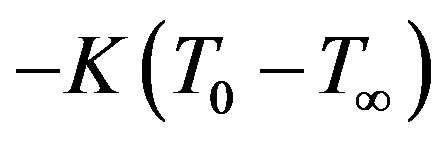 equal to 3, 30 and 300 K for a reference temperature of Tref = 300 K.
equal to 3, 30 and 300 K for a reference temperature of Tref = 300 K.
In order to obtain a local similarity solution in time of the problem under consideration, we introduce a time dependent length scale d as
 . (9)
. (9)
With this similarity parameter d, a similarity variable is then introduced as
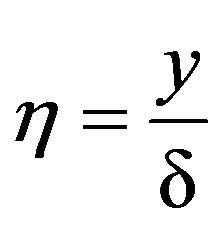 (10)
(10)
In terms of this length scale, a convenient solution of the Equation (1) can be taken as
 (11)
(11)
where v0 is the mass transfer parameter, which is positive for suction and negative for injection. Following M. M. A. Samad and M. M. Rahman [27], we see that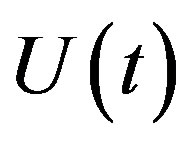 ,
, 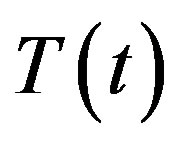 and
and  are now considered to have the following form:
are now considered to have the following form:
 (12)
(12)
where n is a non-negative integer and, U0, T0 and C0 are respectively the free stream velocity, mean temperature and concentration. Here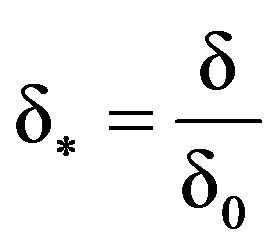 ,
,  is the value of d at t = t0.
is the value of d at t = t0.
Now to make the Equations (2)-(4) dimensionless, we introduce the following transformations:
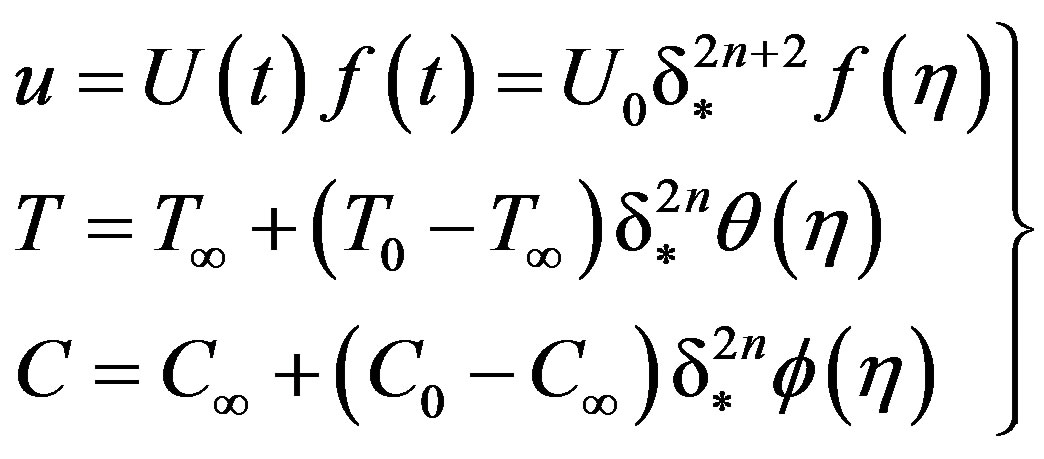 (13)
(13)
Now introducing all the above similarity variables in Equations (2) and (3) we have the following dimensionless ordinary non-linear differential equations
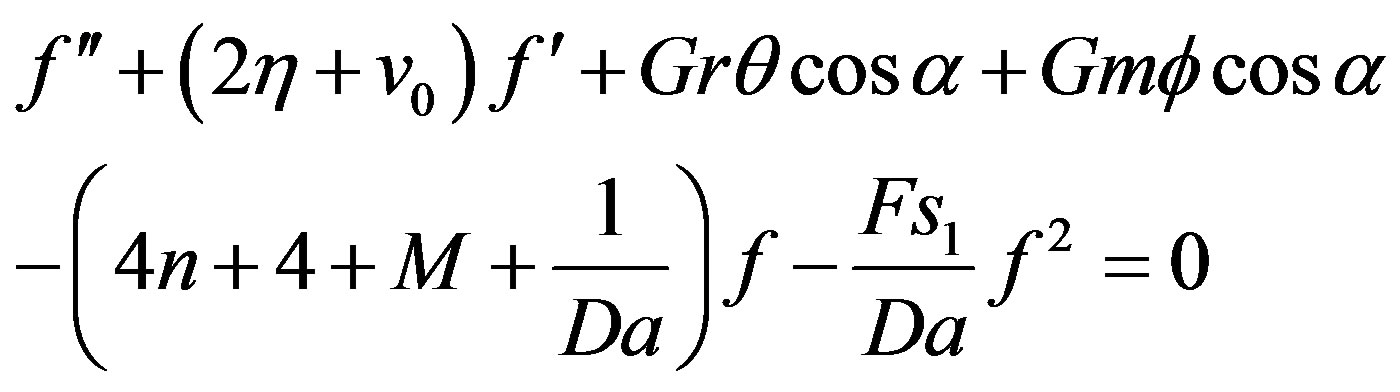 (14)
(14)
 (15)
(15)
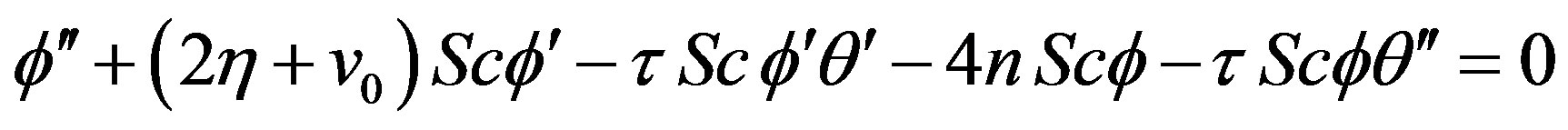 (16)
(16)
where  is the local Grashof number,
is the local Grashof number, 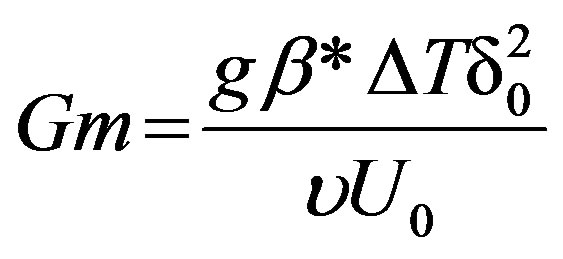 is the modified Grashof number,
is the modified Grashof number, 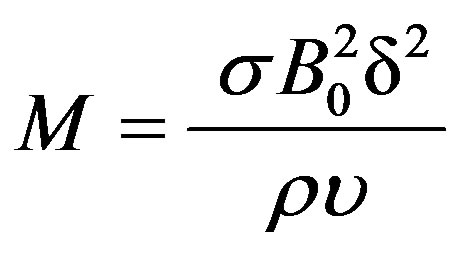 is the local magnetic field parameter,
is the local magnetic field parameter,  is the Forchhemier number and
is the Forchhemier number and 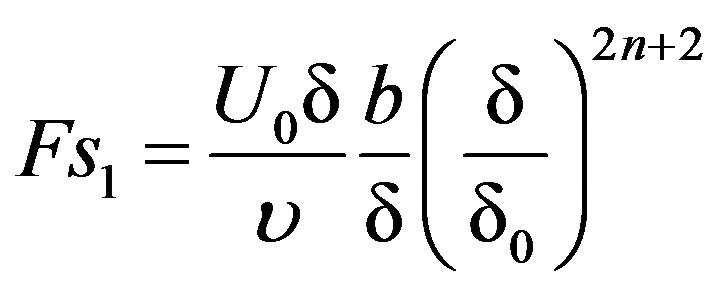 is the modified Forchhemier number,
is the modified Forchhemier number, 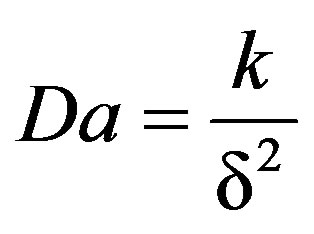 is the Darcy number,
is the Darcy number, 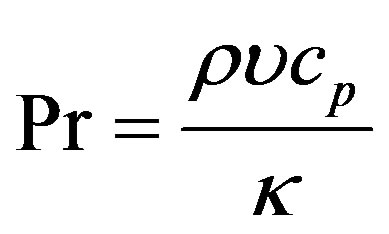 is the Prandtl number,
is the Prandtl number, 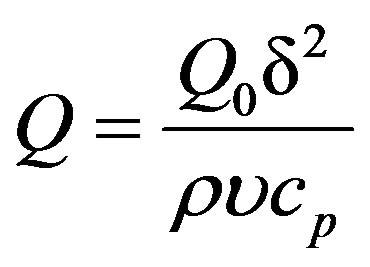 is the heat generation,
is the heat generation, 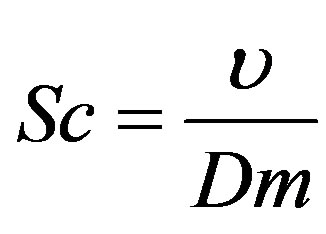 is the Schmidt number and
is the Schmidt number and 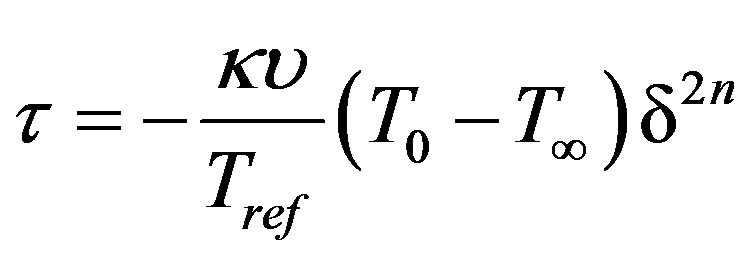 is the Thermophoresis parameter.
is the Thermophoresis parameter.
As a result the corresponding boundary conditions for t > 0 take the form
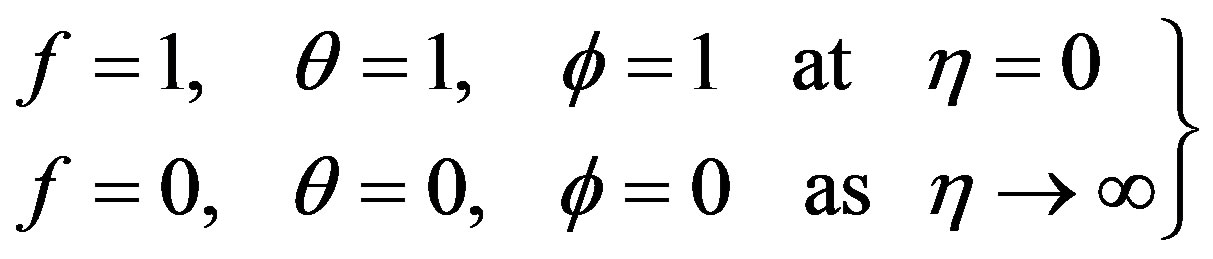 (17)
(17)
Skin-Friction Coefficient, Nusselt Number and Stanton Number
The parameters of engineering interest for the present problem are the skin-friction coefficient, local Nusselt number and the local Stanton number which indicate physically wall shear stress, rate of heat transfer and wall deposition flux respectively.
The skin-friction coefficient is given by
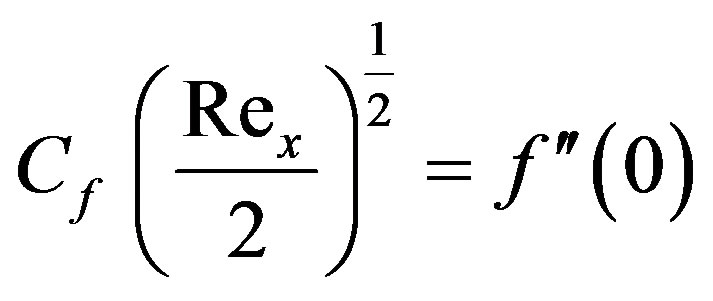 , (18)
, (18)
the local Nusselt number may be written as
 (19)
(19)
and the Stanton number can be written as
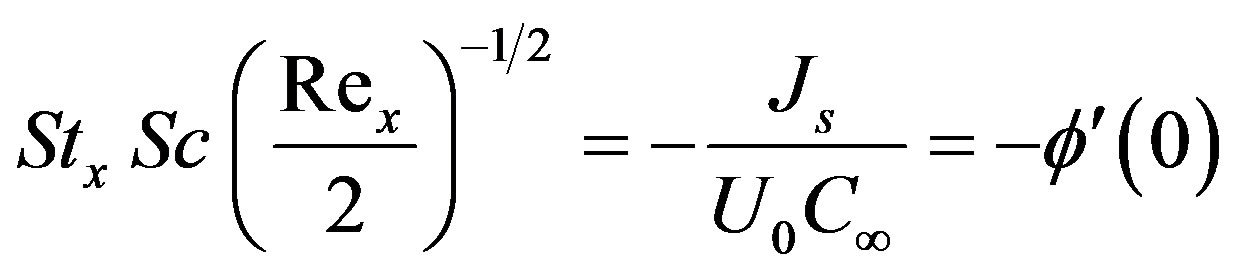 i.e.,
i.e.,
 (20)
(20)
Thus the values proportional to the skin-friction coefficient, Nusselt number and the Stanton number are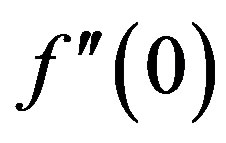 ,
,  and
and  respectively.
respectively.
3. Numerical Computation
The numerical solutions of the nonlinear differential Equations (14)-(16) under the boundary condition (17) have been performed by applying a shooting method namely P. R. Nachtsheim and P. Swigert [28] iteration technique (guessing the missing value) along with sixth order Runge-Kutta integration scheme. We have chosen a step size of Dh = 0.01 to satisfy the convergence criterion of 10−6 in all cases. The value of h¥ was found to each iteration loop by h¥ =h¥ + Dh. The maximum value of h¥ to each group of parameters v0, Gr, Gm, α, M, Da, Fs1, n, Pr, Q, Sc and τ determined when the value of the unknown boundary conditions at h = 0 not change to successful loop with error less than 10−6.
In order to verify the effects of the step size (Dh) we ran the code for our model with three different step sizes as Dh = 0.01, Dh = 0.005, Dh = 0.001 and in each case we found excellent agreement among them. Figures 2-4 show the velocity, temperature and concentration profiles for different step sizes respectively considering v0 = 0.1, Gr = 10, Gm = 10, α = 30˚, M = 0.5, Da = 2.0, Fs1 = 1.0, n = 1, Pr = 0.71, Q = 5.0, Sc = 0.22 and τ = 0.5.
4. Results and Discussion
For the purpose of discussing the results, the numerical calculations are presented in the form of non-dimensional velocity and temperature profiles. Numerical computations have been carried out for different values of the suction parameter (v0), Grashof number (Gr), modified Grashof number (Gm), angle of the inclination , magnetic field parameter (M), Darcy number (Da), modified Forchhemier number (Fs1), constant parameter (n), Prandtl number (Pr), heat generation (Q), Schmidt number (Sc) and the thermophoresis parameter (τ). The values of Grashof number (Gr) are taken be large from
, magnetic field parameter (M), Darcy number (Da), modified Forchhemier number (Fs1), constant parameter (n), Prandtl number (Pr), heat generation (Q), Schmidt number (Sc) and the thermophoresis parameter (τ). The values of Grashof number (Gr) are taken be large from

Figure 2. Velocity profiles for different values of Dh.
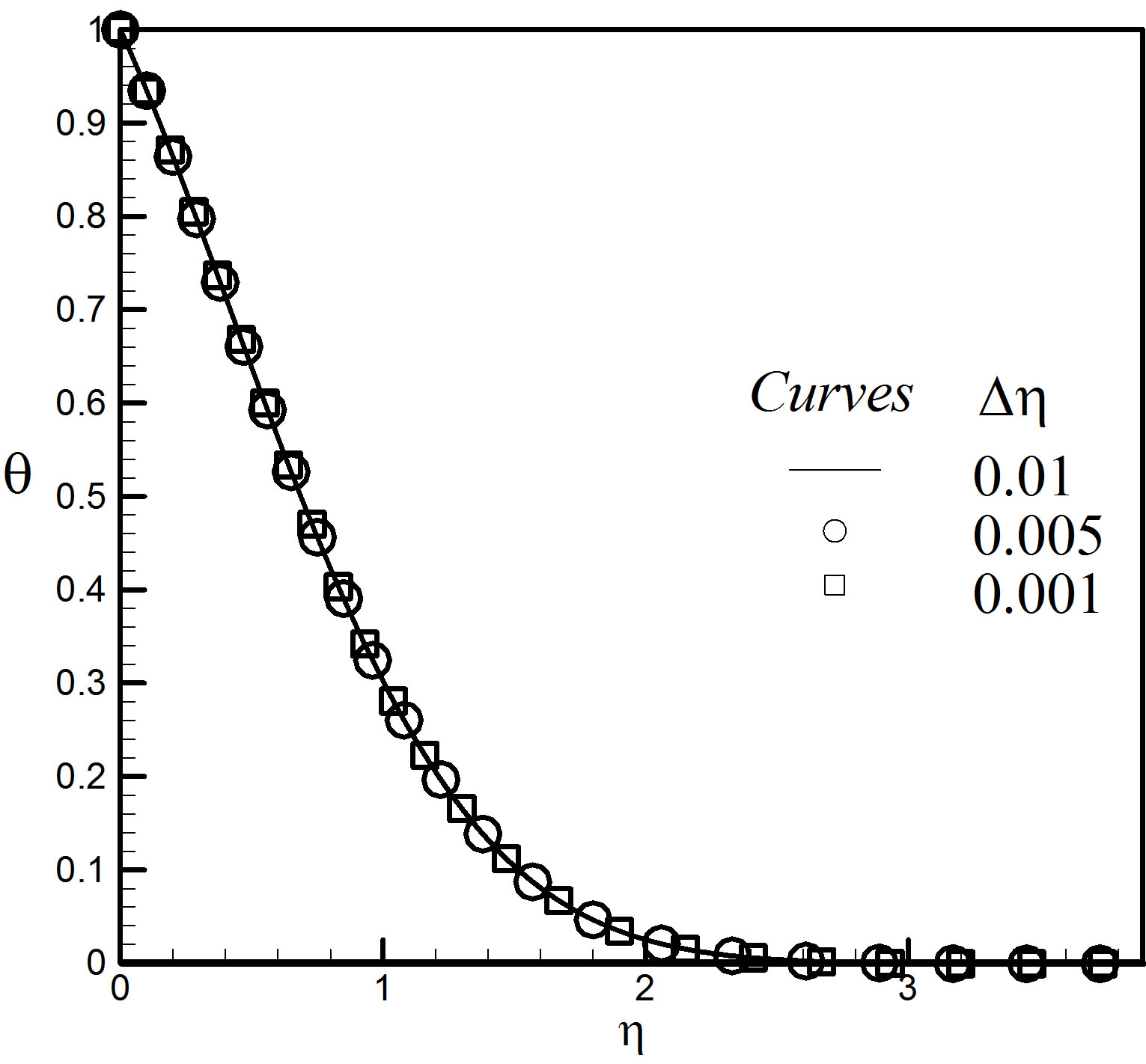
Figure 3. Temperature profiles for different values of Dh.

Figure 4. Concentration profiles for different values of Dh.
the physical point of view. The large Grashof number values correspond to free convection problem.
Figures 5-7 display the effects of the suction parameter v0 on the velocity, temperature and concentration profiles respectively. It is observed that, when suction v0 increases, all the profiles decrease. The effects on velocity and temperature profiles are significant but on concentration are small. The decreasing suction restrains the heat transfer coefficient.
We take α = 0˚, 30˚, 40˚ and 60˚ as the values of the angle of the inclination of the plate to explain the effect of α. As α increases, the effect of the buoyancy force decreases because of the multiplication factor cosα and hence the velocities decrease with the increase of α swiftly shown in Figure 8. Figure 9 explains that the temperatures as well as the concentration profiles are completely beyond the influence of the inclination of the plate.
M = 0, 0.5, 1.0, 2.0 are taken to examine the effect of the magnetic field parameter M on the velocity, temperature and concentration fields shown in Figures 10

Figure 5. Velocity profiles for different values of v0.

Figure 6. Temperature profiles for different values of v0.
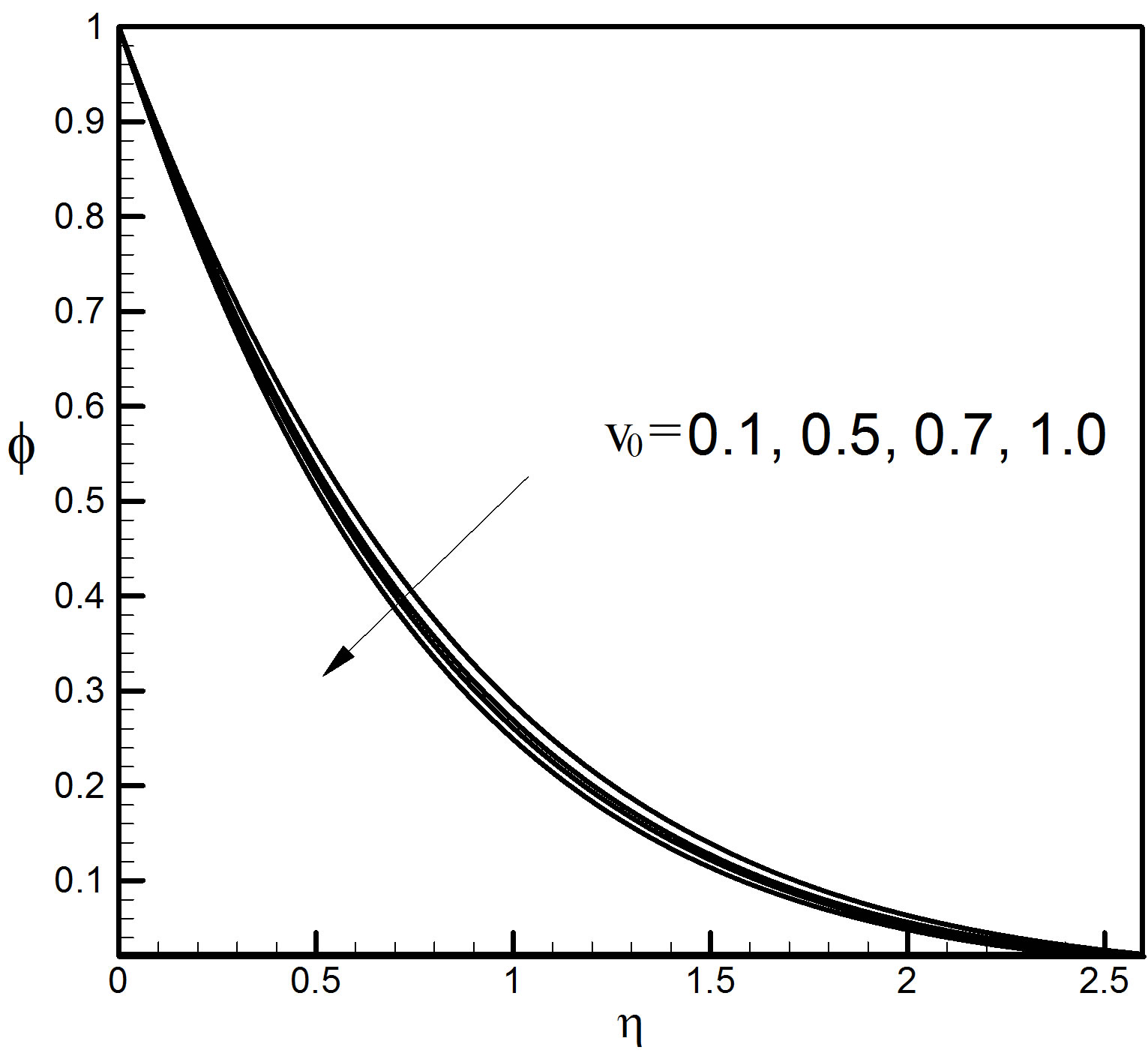
Figure 7. Concentration profiles for different values of v0.
and 11. Figure 8 states that the velocity increases faintly with the increase of M. In Figure 11 there is no outcome on the temperature and concentration profiles due the distinction of the values of M.
We chose Da = 1.0, 2.0, 3.0, 4.0 to analyze the effect

Figure 8. Velocity profiles for different values of a.
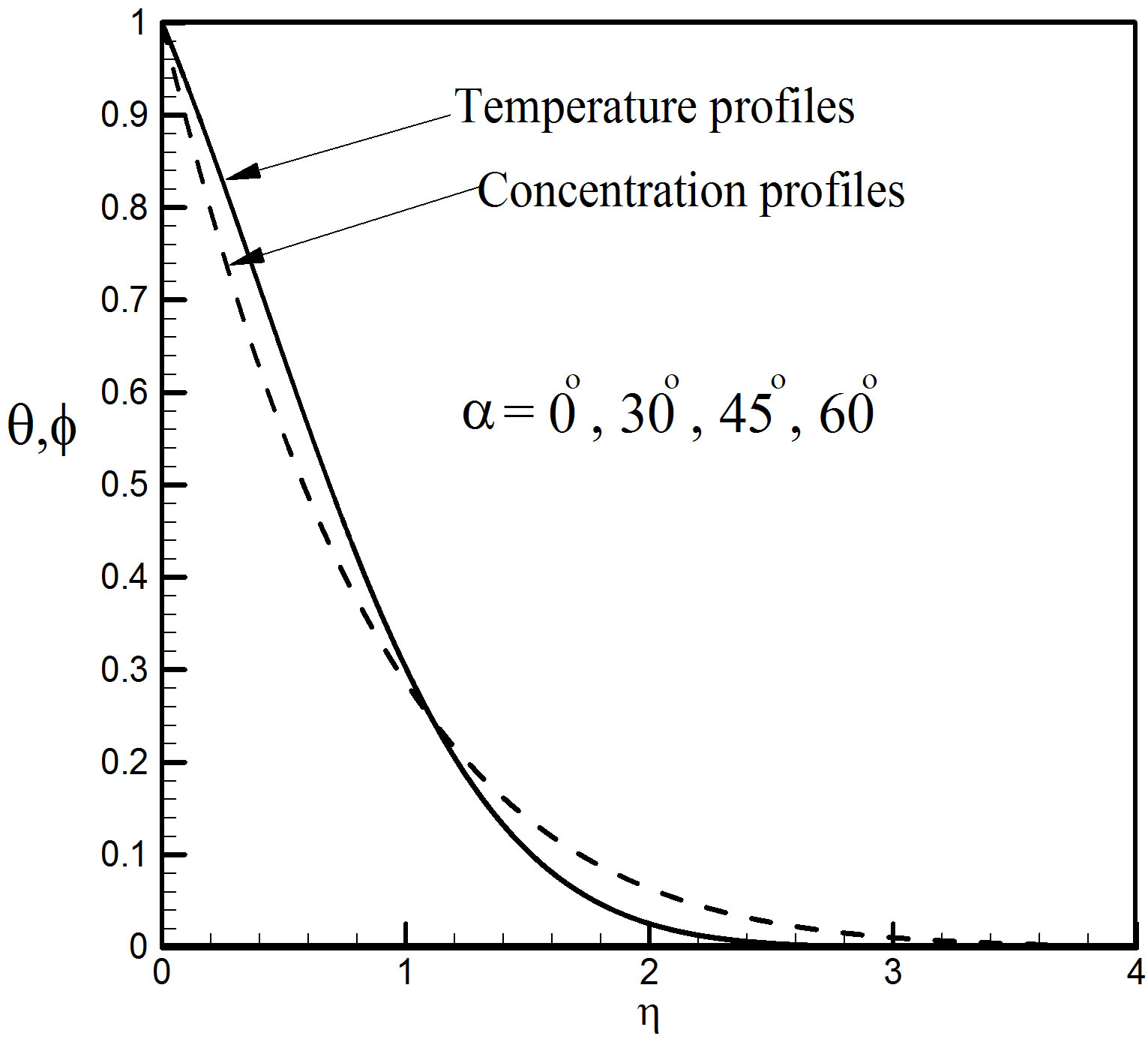
Figure 9. Temperature and concentration profiles for different values of a.
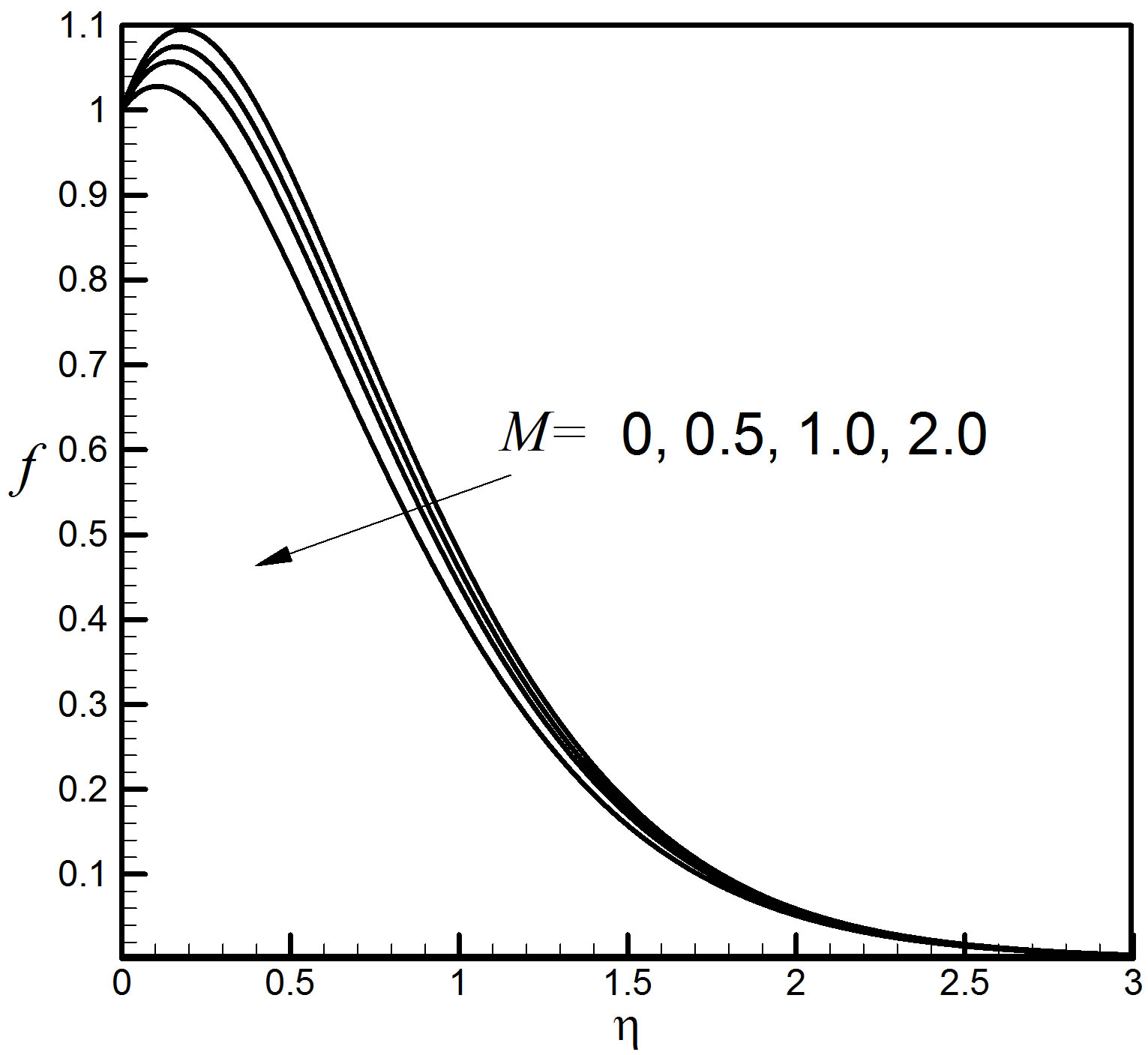
Figure 10. Velocity profiles for different values of M.
of the Darcy number Da on the velocity, temperature and concentration fields shown in Figures 12 and 13 expressing that the velocity increases slightly with the increase of Da but no effect is shown on the temperature
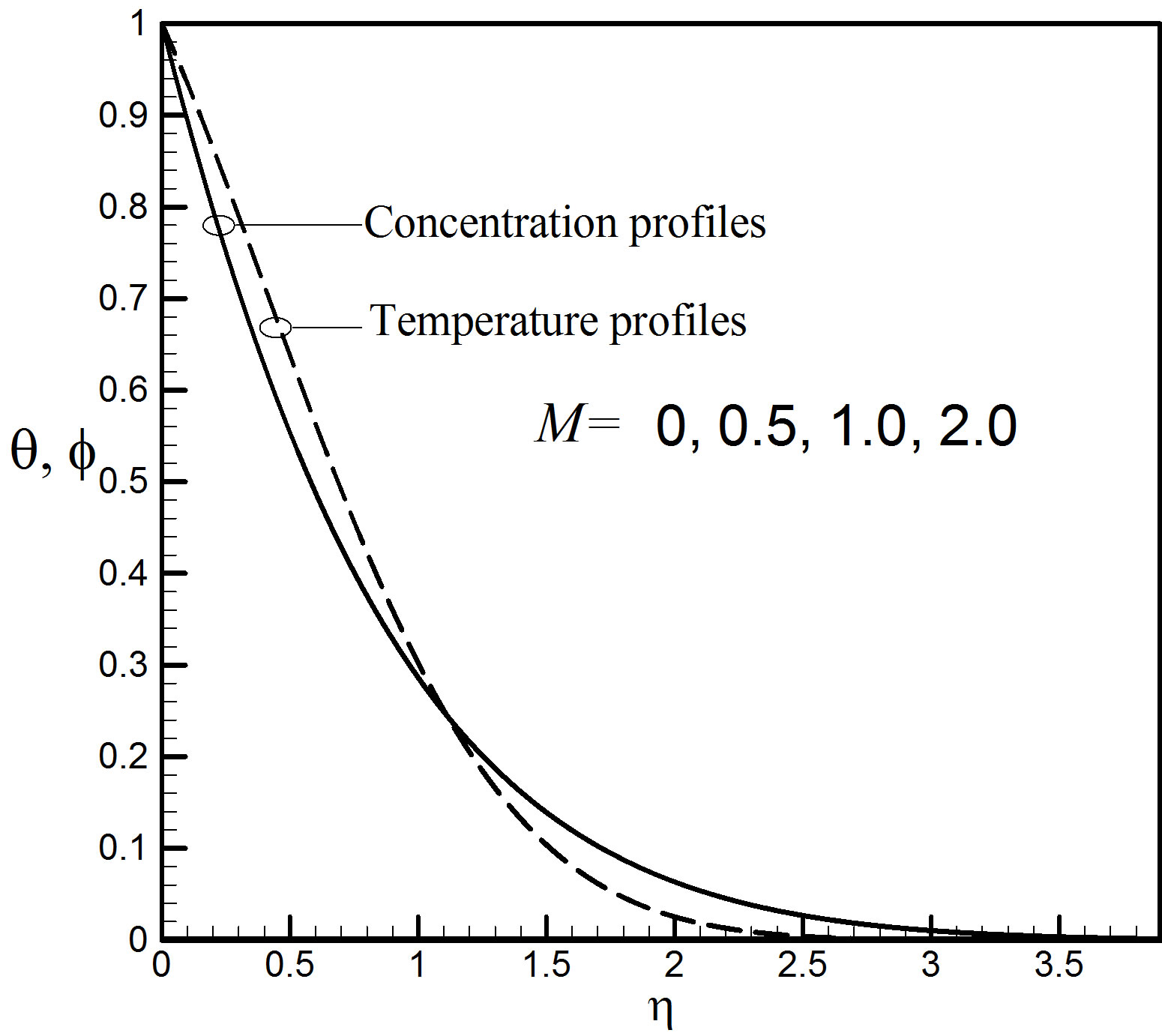
Figure 11. Temperature and concentration profiles for different values of M.
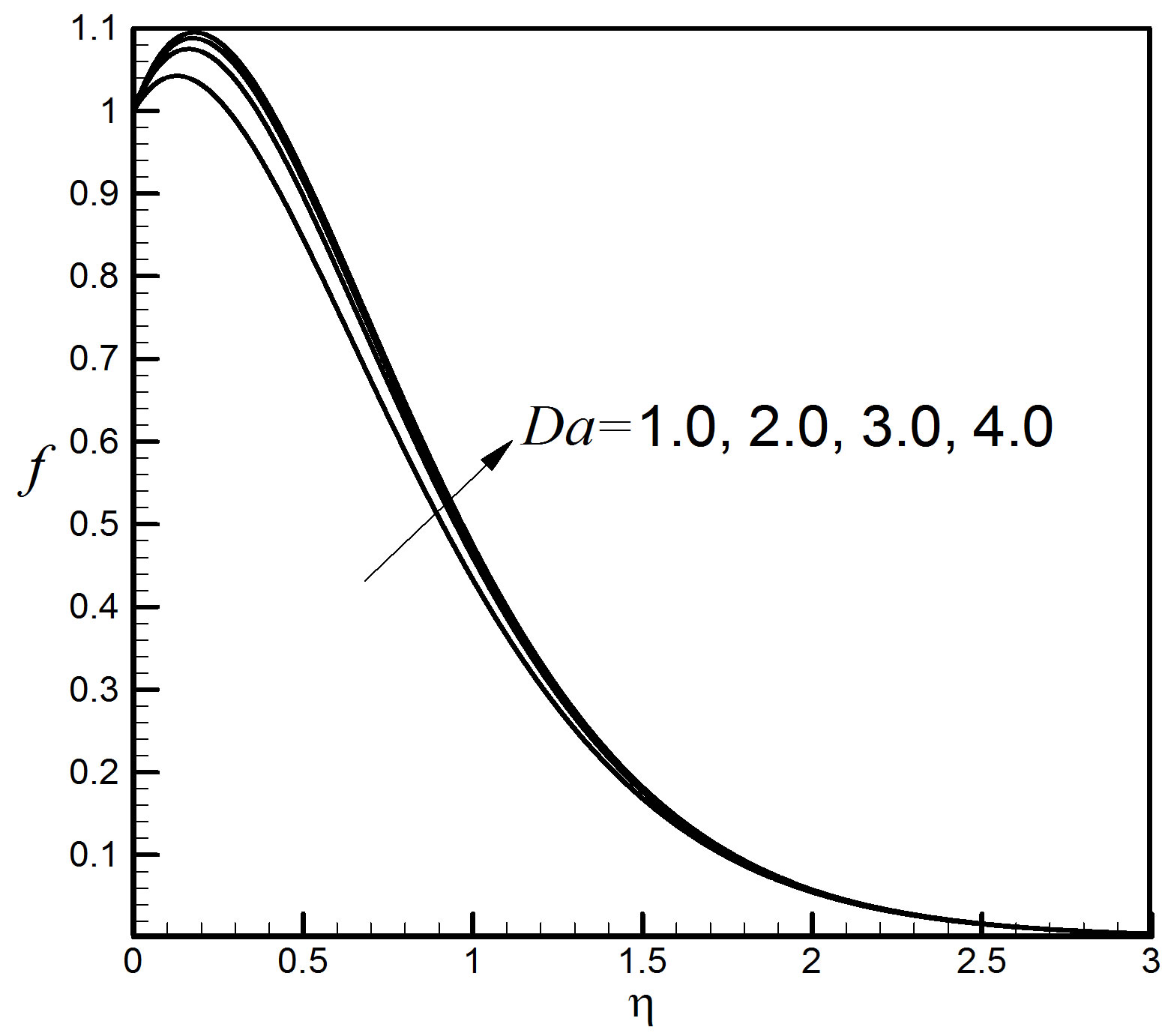
Figure 12. Velocity profiles for different values of Da.
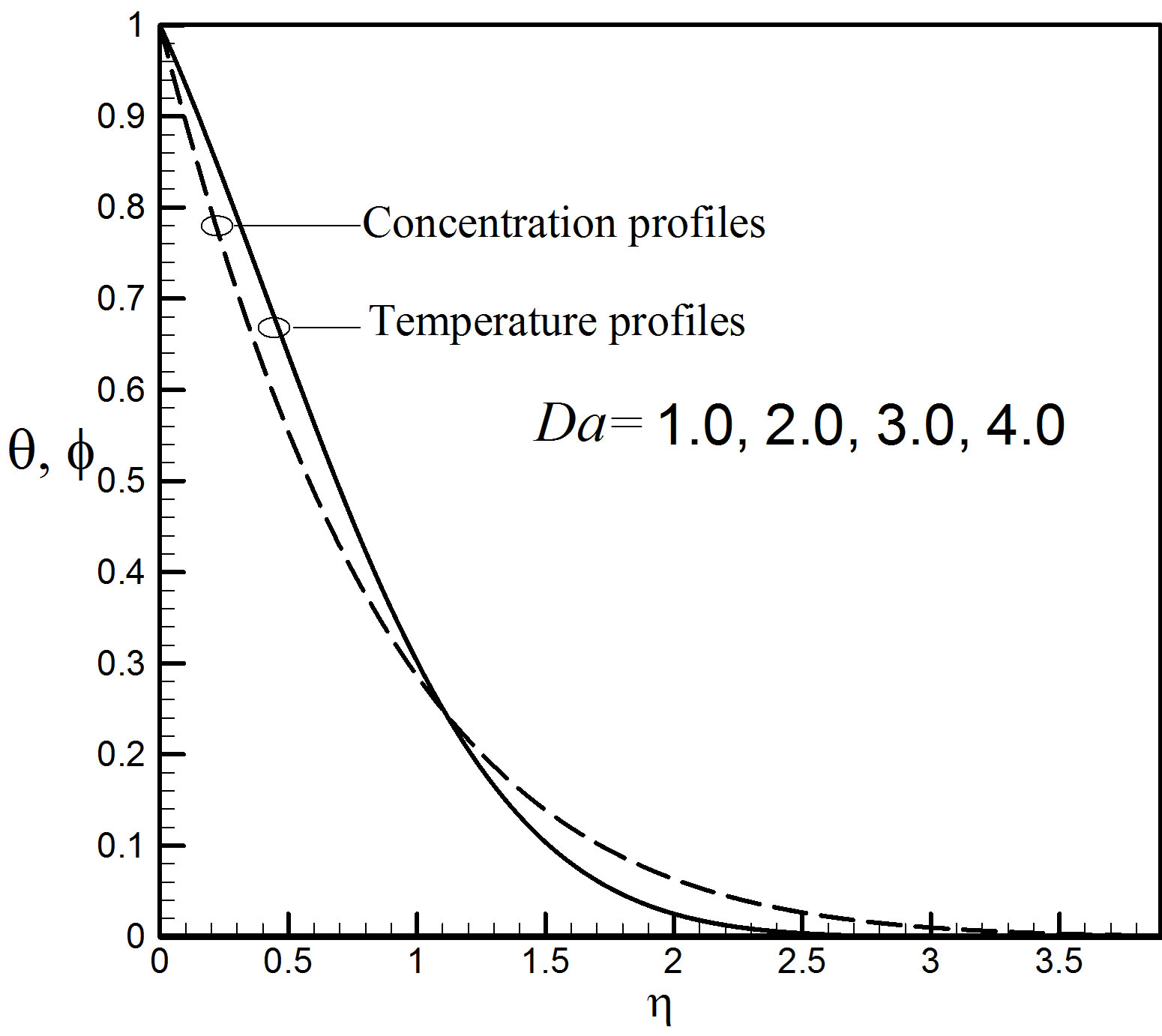
Figure 13. Temperature and concentration profiles for different values of Da.
and concentration profiles due the distinction of the values of Da.
Here n = 1, 2, 3, 5 are considered to demonstrate the effect of the nonlinearity constant parameter. Figures 14-16 represent the control of the constant parameter n to all the profiles. All the profiles decrease with the increase of n. The effects of n are very significant and smooth on the distributions.
We have illustrated non-dimensional velocity, tem-

Figure 14. Velocity profiles for different values of n.
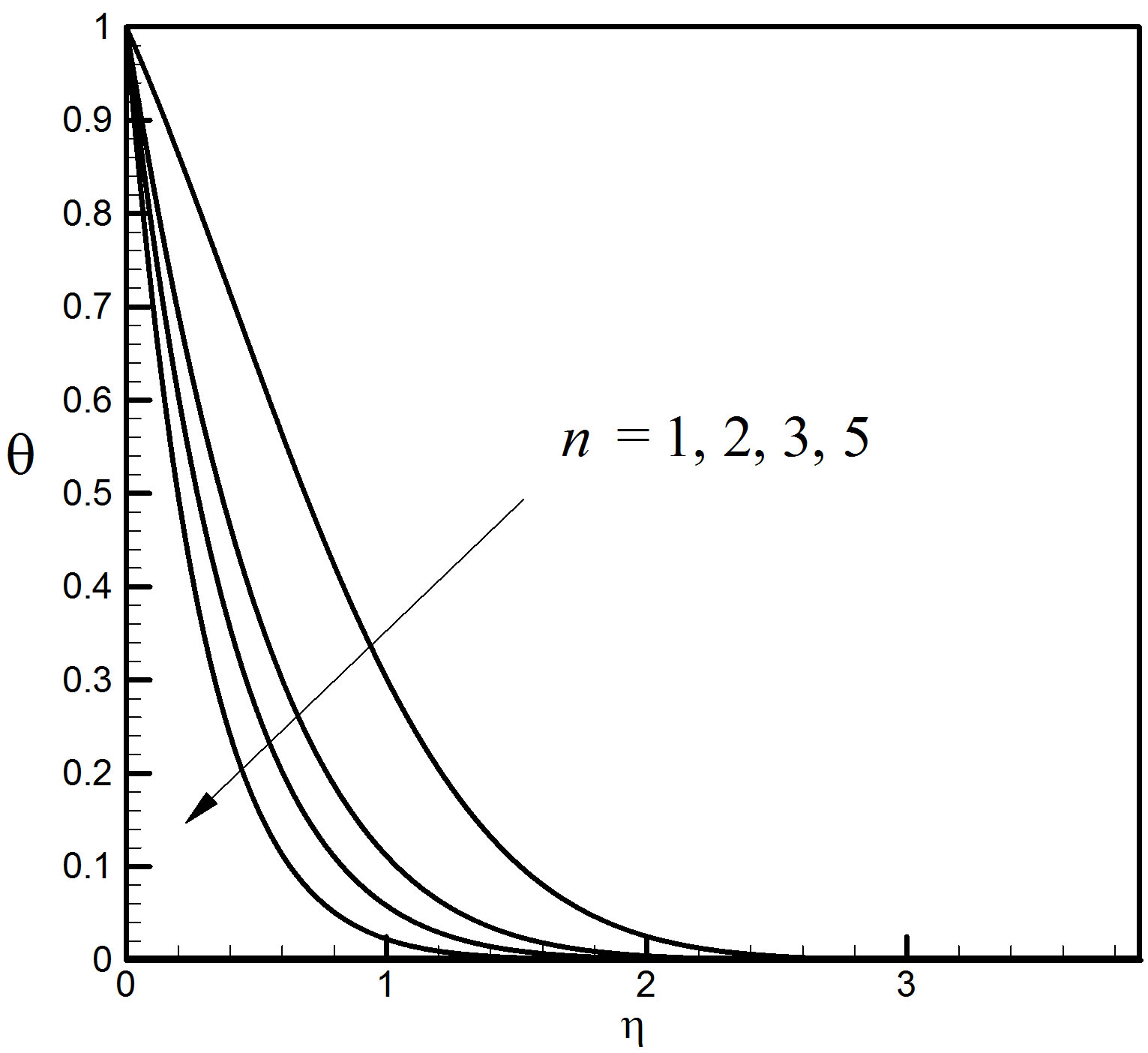
Figure 15. Temperature profiles for different values of n.
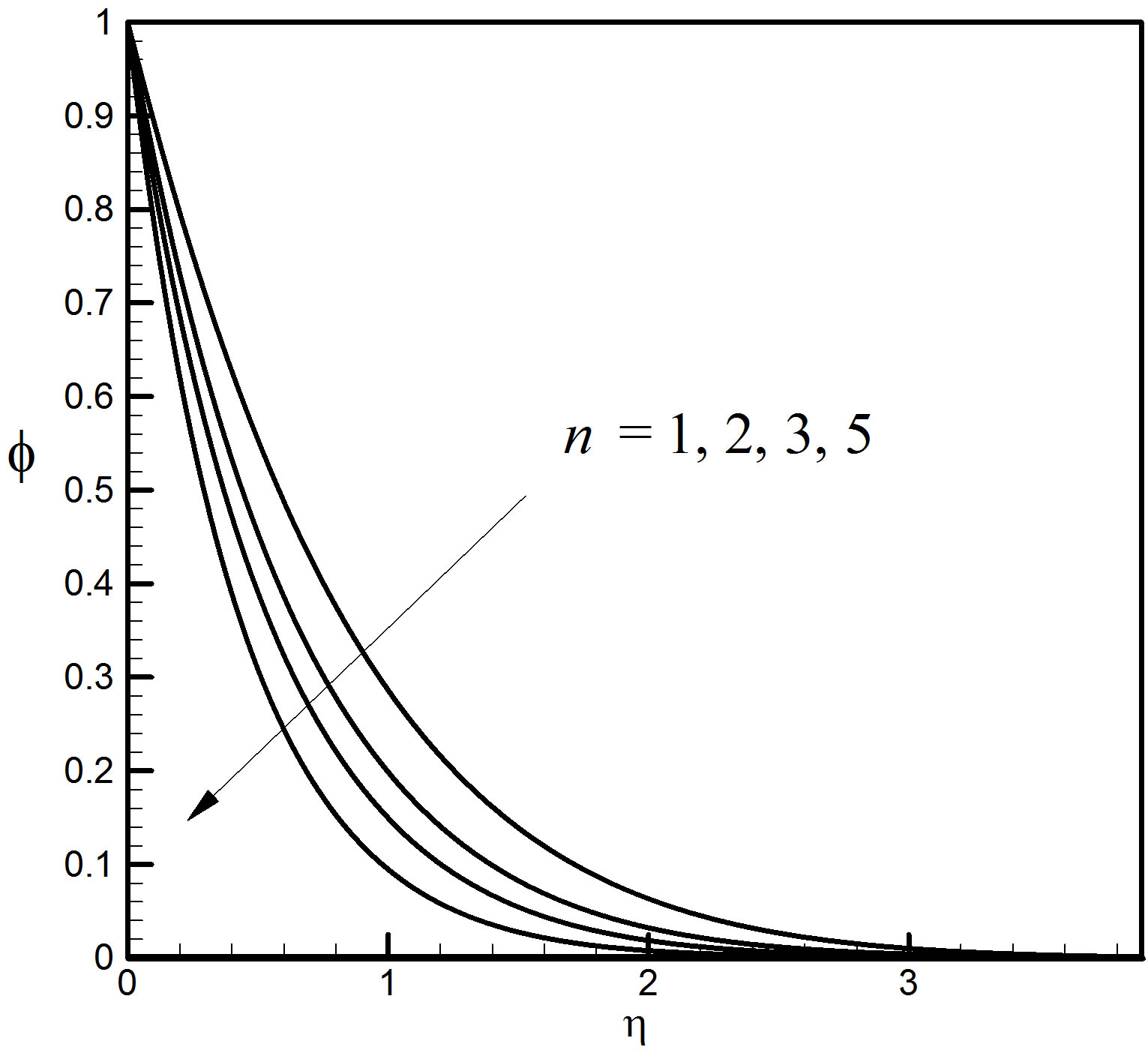
Figure 16. Concentration profiles for different values of n.
perature and concentration profiles against h for some representative values of the heat source parameter Q = 1, 3, 5, 7 in Figures 17 and 18. The positive value of Q represents source i.e. heat generation in the fluid. From Figure 17, it is observed that due to the generation of heat the buoyancy force increases which in turn gives higher velocity in the boundary layer. This is corroborated by Figure 18 where it is seen that the temperatures indicated by solid lines do indeed rapidly increase as Q increases and there are very tiny fluctuations in the concentration profiles pointed out by dashed lines.
In Figures 19 and 20 we have plotted the dimensionless velocity, temperature and concentration profiles showing the effect of thermophoretic parameter τ. The dropping effect of τ on velocity is seen in Figure 19. There is no effect on temperature profiles marked by solid line for the variation of the values of τ in Figure 20. We also observe from Figure 20 specified by the dashed lines that the thermophoretic parameter τ affects the concentration profiles very considerably. The concentration profiles decrease with the increase of τ.
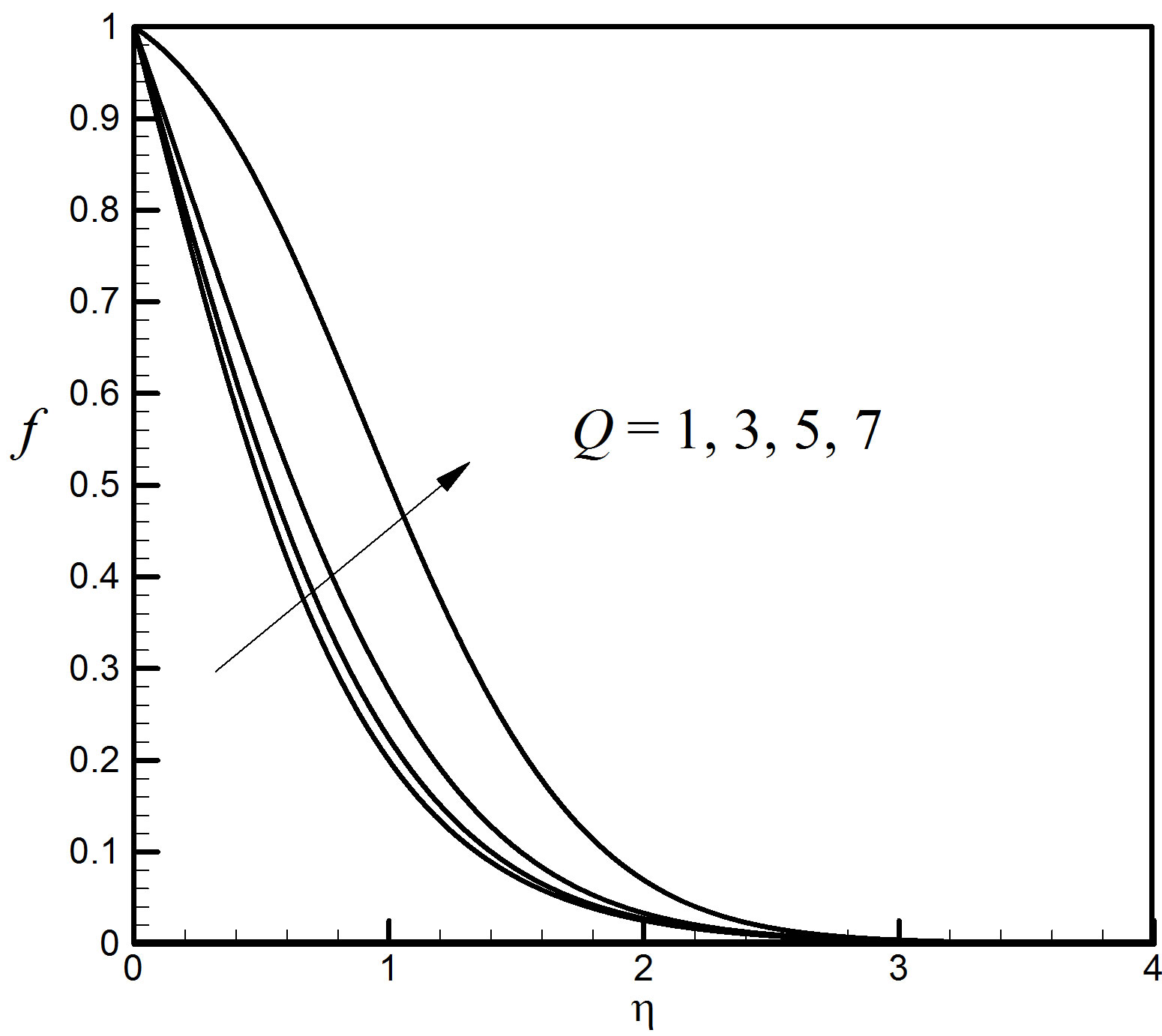
Figure 17. Velocity profiles for different values of Q.
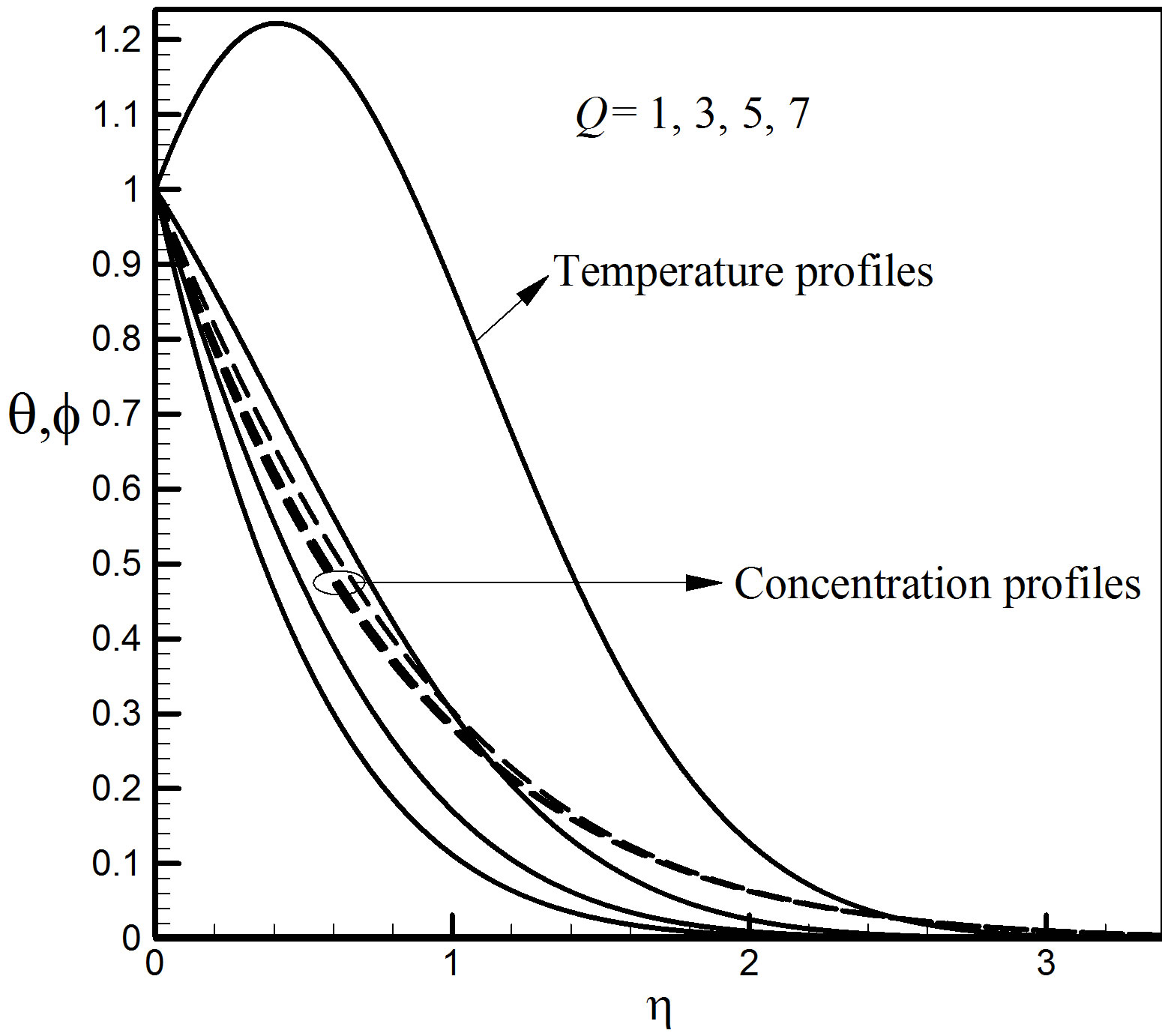
Figure 18. Temperature and concentration profiles for different values of Q.
Finally, the effects of various parameters on the skin friction Cf, local Nusselt number Nu and local Sherwood number Sh are shown in Tables 1-5.
5. Conclusions
In this paper we have studied the thermal radiation interaction with unsteady MHD boundary layer flow past a continuously moving vertical plate with suction. From the present study we can make the following conclusions:
• Using suction boundary layer growth can be controlled. Suction stabilizes the hydrodynamic, thermal
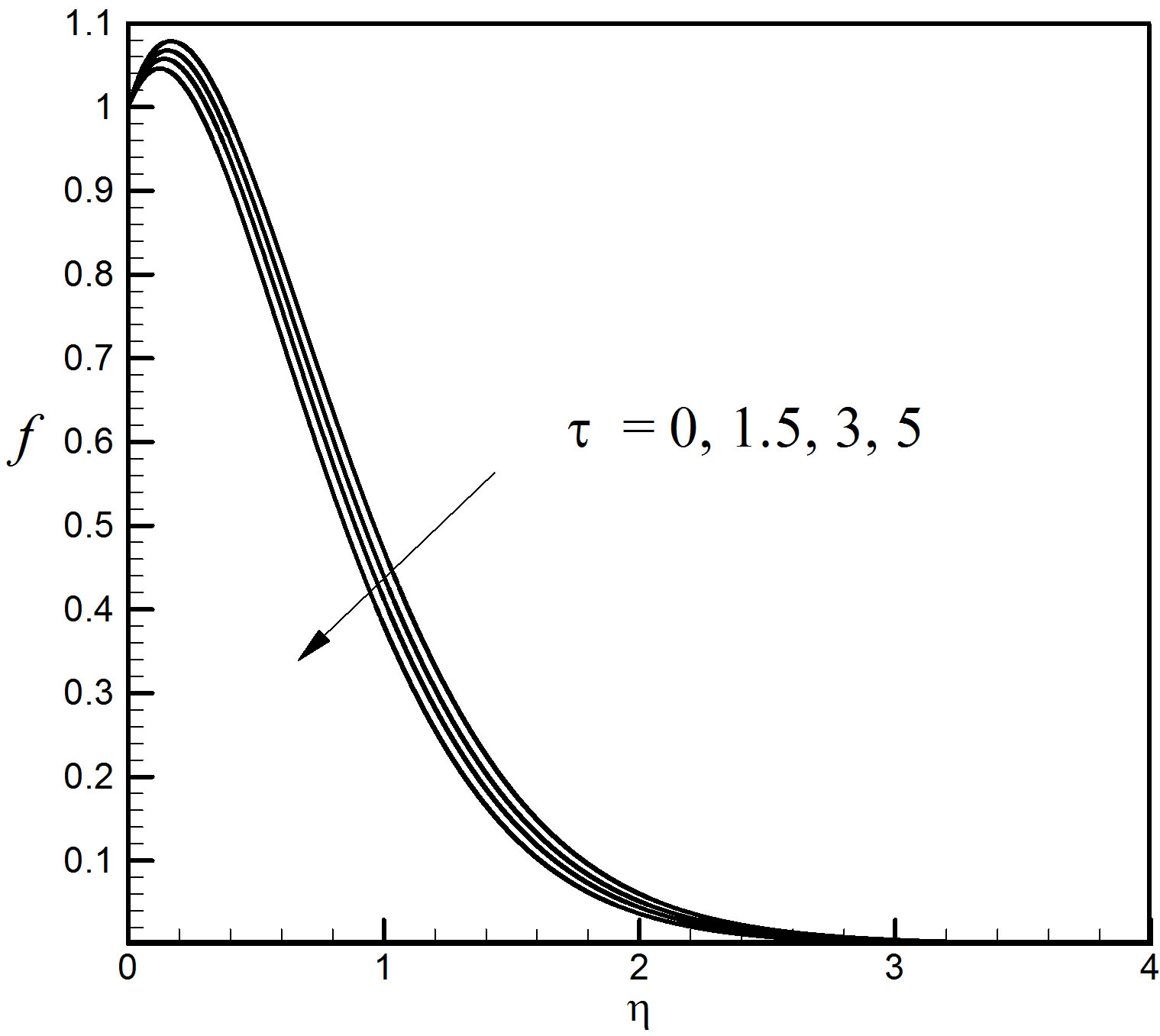
Figure 19. Velocity profiles for different values of τ.
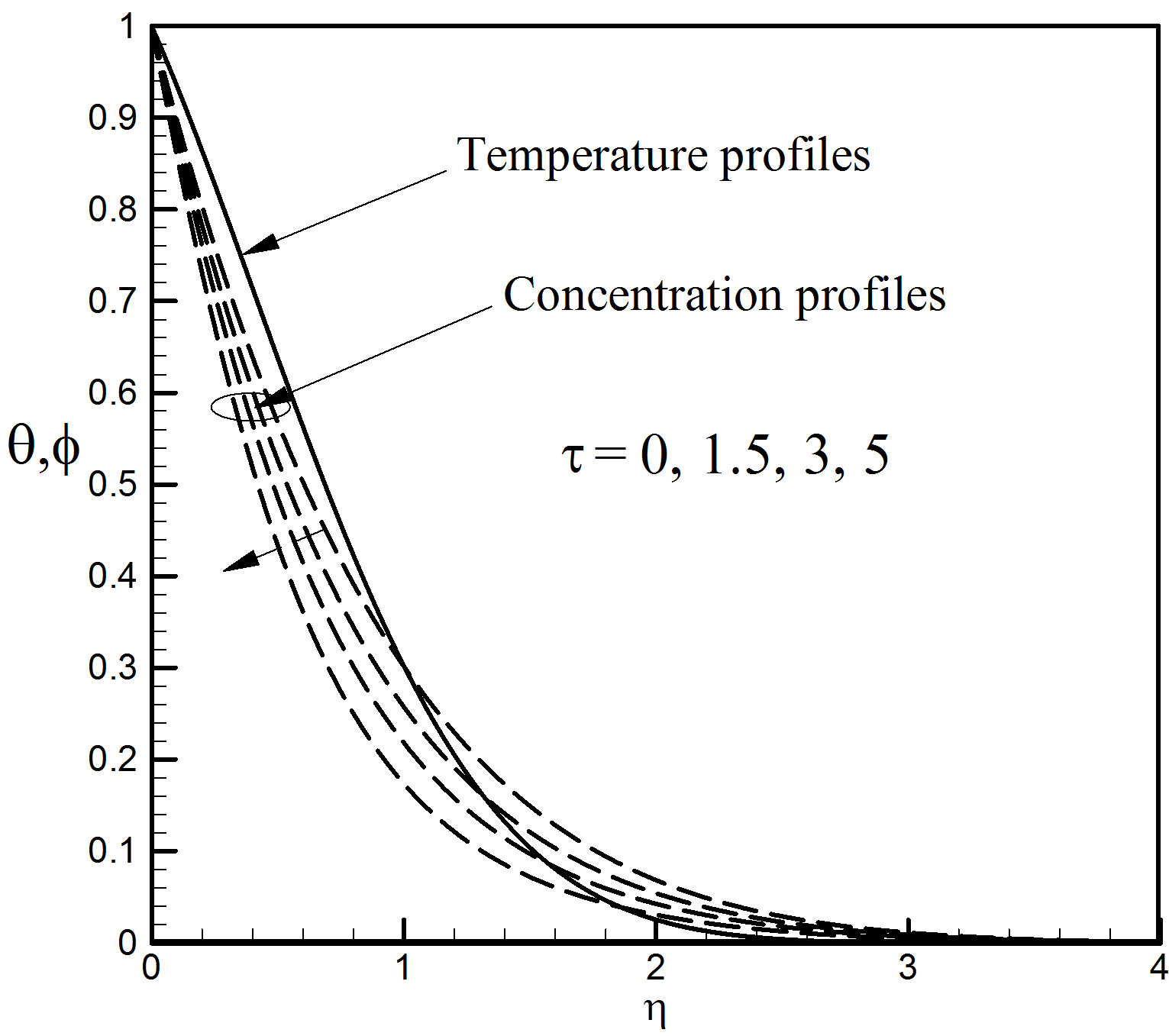
Figure 20. Temperature and concentration profiles for different values of τ.
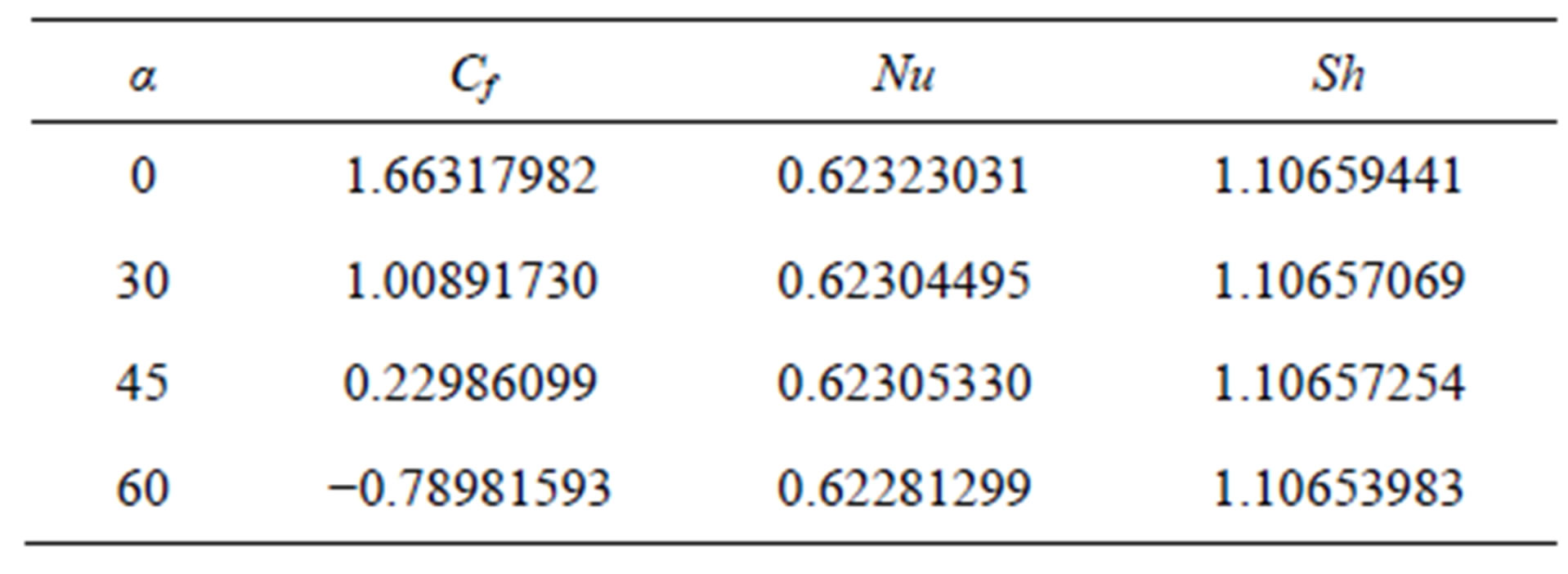
Table 1. Cf, Nu and Sh for different values of α.

Table 2. Cf, Nu and Sh for different values of Q.
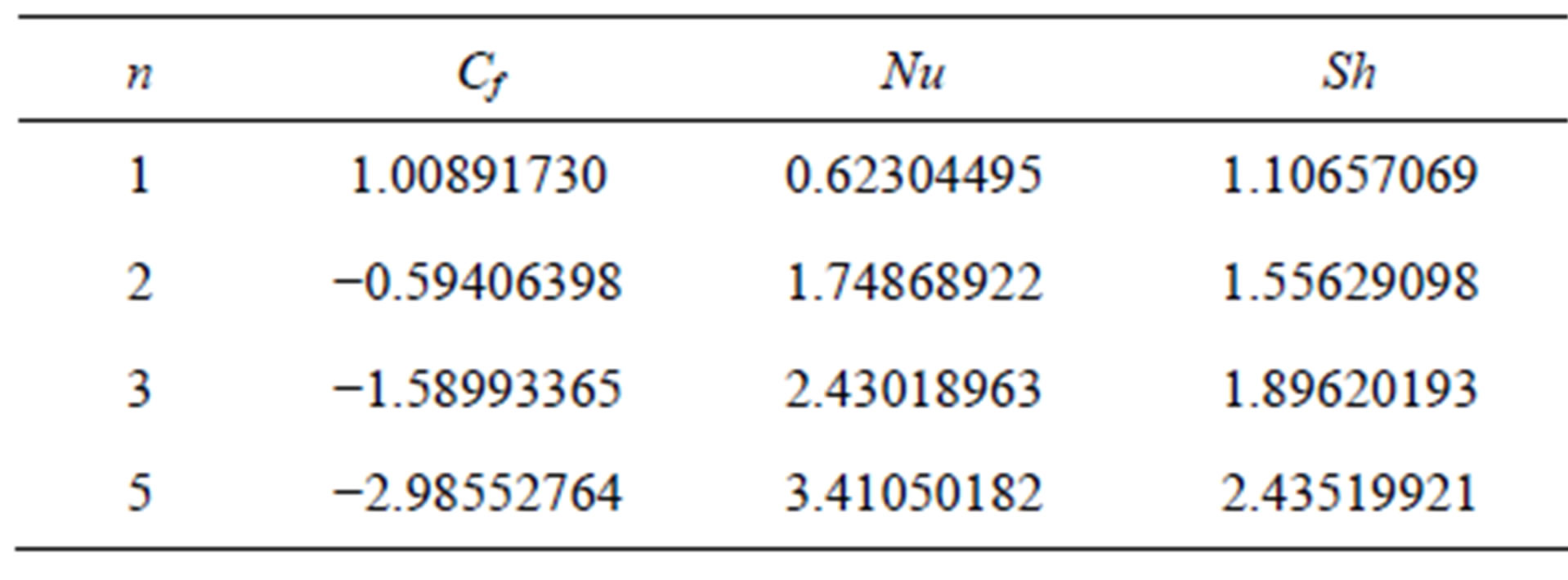
Table 3. Cf, Nu and Sh for different values of n.

Table 4. Cf, Nu and Sh for different values of Da.
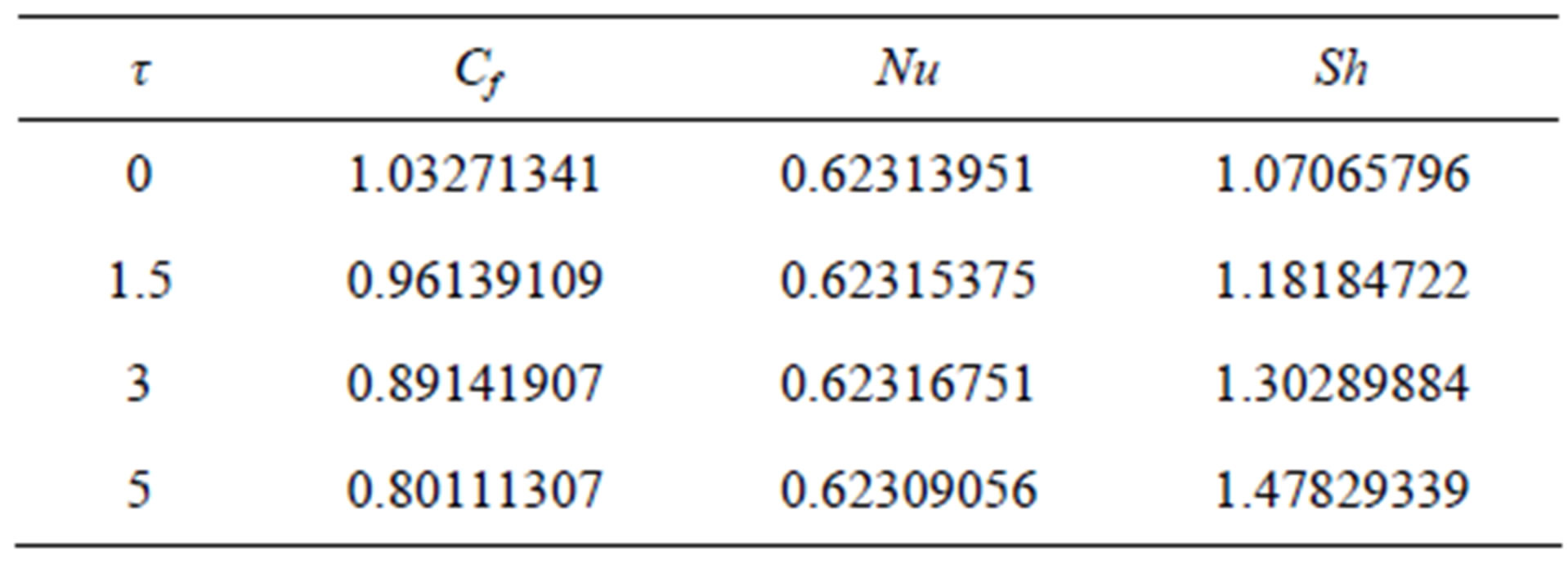
Table 5. Cf, Nu and Sh for different values of τ.
as well as concentration boundary layers growth.
• The velocity profiles increase whereas temperature profiles decrease with an increase of the free convection current.
• Magnetic field has significant effect on velocity field and retards the motion of the fluid.
• Velocity profiles increase with the increase of Darcy number.
• Thermophoretic number τ has considerable effect on concentration profiles.
REFERENCES
- S. Ostrach, “An Analysis of Laminar Free-Convection Flow and Heat Transfer about a Flat Plate Parallel to the Direction of the Generating Body Force,” Technical Note, NACA Report, Washington, 1952.
- B. C. Sakiadis, “Boundary-Layer Behavior on Continuous Solid Surfaces: I. Boundary-Layer Equations for TwoDimensional and Axisymmetric Flow,” AIChE Journal, Vol. 7, No. 1, 1961, pp. 26-28. Hdoi:10.1002/aic.690070108
- L. E. Erickson, L. T. Fan and V. G. Fox, “Heat and Mass Transfer on a Moving Continuous Flat Plate with Suction or Injection,” Industrial Engineering and Chemical Fundamentals, Vol. 5, No. 1, 1966, pp. 19-25. Hdoi:10.1021/i160017a004
- S. L. Goren, “Thermophoresis of Aerosol Particles in Laminar Boundary Layer on Flat Plate,” Journal of Colloid Interface Science, Vol. 61, No. 1, 1977, pp. 77-85. Hdoi:10.1016/0021-9797(77)90416-7
- E. M. Sparrow, “Radiation Heat Transfer,” Augmented Edition, Hemisphere Publishing Corp., Washington DC, 1978.
- R. S. R. Gorla, “Unsteady Mass Transfer in the Boundary Layer on a Continuous Moving Sheet Electrod,” Journal of the Electrochemical Society, Vol. 125, No. 6, 1978, pp. 865-869. Hdoi:10.1149/1.2131569
- G. M. Homsy, F. T. Geyling and K. L. Walker, “Blasius Series for Thermophoretic Deposition of Small Particles,” Journal of Colloid Interface Science, Vol. 83, No. 2, 1981, pp. 495-501. Hdoi:10.1016/0021-9797(81)90345-3
- A. Raptis and C. Perdikis, “Unsteady Flow through a Porous Medium in the Presence of Free Convection,” International Communications in Heat and Mass Transfer, Vol. 12, No. 6, 1985, pp. 697-704. Hdoi:10.1016/0735-1933(85)90022-3
- M. Epstein, G. M. Hauser and R. E. Henry, “Thermophoretic Deposition of Particles In Natural Convection Flow from a Vertical Plate,” Journal of Heat Transfer, Vol. 107, No. 2, 1985, pp. 272-276. Hdoi:10.1115/1.3247410
- M. A. Alabraba, A. R. Bestman and A. Ogulu, “Laminar Convection in Binary Mixed of Hydromagnetic Flow with Radiative Heat Transfer-I, II,” Astrophysics and Space Science, Vol. 195, No. 2, 1992, pp. 431-439, 441- 445. Hdoi:10.1007/BF00646774
- A. Sattar and M. Hossain, “Unsteady Hydromagnetic Free Convection Flow with Hall Current and Mass Transfer along an Accelerated Porous Plate with Time Dependent Temperature and Concentration,” Canadian Journal of Physics, Vol. 70, No. 5, 1992, pp. 369-375. Hdoi:10.1139/p92-061
- M. A. Hossain and H. S. Takhar, “Radiation Effect on Mixed Convection along a Vertical Plate with Uniform Surface Temperature,” Heat and Mass Transfer, Vol. 31, No. 4, 1996, pp. 243-248. Hdoi:10.1007/BF02328616
- J.-S. Lin, C.-J. Tsai and C.-P. Chang, “Suppression of Particle Deposition in Tube Flow by Thermophoresis,” Journal of Aerosol Science, Vol. 35, No. 2004, pp. 1235- 1250. Hdoi:10.1016/j.jaerosci.2004.05.007
- M. A. Seddek, “Finite-Element Method for the Effects of Chemical Reaction, Variable Viscosity, Thermophoresis and Heat Generation/Absorption on a Boundary-Layer Hydromagnetic Flow with Heat and Mass Transfer over a Heat Surface,” Journal of Acta Machanica, Vol. 177, 2005, pp. 1-18.
- M. S. Alam, M. M. Rahman and M. A. Sattar, “Similarity Solutions for Hydromagnetic Free Convective Heat and Mass Transfer Flow along a Semi-Infinite Permeable Inclined Flat Plate with Heat Generation and Thermophoresis,” Nonlinear Analysis: Modelling and Control, Vol. 12, No. 4, 2007, pp. 433-445.
- M. A. Samad and M. E. Karim, “Thermal Radiation Interaction with Unsteady MHD Flow past a Vertical Flat Plate with Time Dependent Suction,” Dhaka University Journal of Science, Vol. 57, No. 1, 2009, pp. 113-118.
- M. A. A. Mahmoud, “Thermal Radiation Effect on Unsteady MHD Free Convection Flow Past a Vertical Plate with Temperature Dependent Viscosity,” Canadian Journal of Chemical Engineering, Vol. 87, No. 1, 2009, pp. 47-52. Hdoi:10.1002/cjce.20135
- M. A. Samad, M. E. Karim and D. Mohammad, “Free Convection Flow through a Porous Medium with Thermal Radiation, Viscous Dissipation and Variable Suction in Presence of Magnetic Field,” Bangladesh Journal of Scientific Research, Vol. 23, No. 1, 2010, pp. 61-72.
- P. Loganathan and P. P. Arasu, “Thermophoresis Effects on Non-Darcy MHD Mixed Convective Heat and Mass Transfer past a Porous Wedge in The Presence of Suction/Injection,” Theoretic Applied Mechanics, Vol. 37, No. 3, 2010, pp. 203-227. Hdoi:10.2298/TAM1003203L
- M. Ferdows, Nazmul and M. Ota, “Thermophoresis and Chemical Reaction Effects on MHD Natural Convective Heat and Mass Transfer Flow in a Rotating Fluid Considering Heat and Mass Fluxes,” Canadian Journal on Science and Engineering Mathematics, Vol. 2, No. 3, 2011, pp. 114-139.
- O. D. Makinde and P. O. Olanrewaju, “Unsteady Mixed Convection with Soret and Dufour Effects past a Porous Plate Moving through a Binary Mixture of Chemical Reacting Fluid,” Chemical Engineering Communications, Vol. 198, No. 7, 2011, pp. 920-938. Hdoi:10.1080/00986445.2011.545296
- N. Ghara, S. L. Maji, S. Das, R. Jana and S. K. Ghosh, “Effects of Hall Current and Ion-Slip on Unsteady MHD Couette Flow,” Open Journal of Fluid Dynamics, Vol. 2, No. 1, 2012, pp. 1-13. Hdoi:10.4236/ojfd.2012.21001
- G. K. Batchelor and C. Shen, “Thermophoretic Deposition of Particles in Gas flowing over Cold Surface,” Journal of Colloid Interface Science, Vol. 107, No. 1, 1985, pp. 21-37. Hdoi:10.1016/0021-9797(85)90145-6
- L. Talbot, R. K. Cheng, A. W. Schefer and D. R. Wills, “Thermophoresis of Particles in a Heated Boundary Layer,” Journal of Fluid Mechanics, Vol. 101, No. 4, 1980, pp. 737-758. Hdoi:10.1017/S0022112080001905
- A. F. Mills, X. Hang and F. Ayazi, “The Effect of Wall Suction and Thermophoresis on Aerosol-Particle Deposition from a Laminar Boundary Layer on a flat Plate,” International Jornal of Heat and Mass Transfer, Vol. 27, No. 7, 1984, pp. 1110-1114. Hdoi:10.1016/0017-9310(84)90127-3
- R. Tsai, “A Simple Approach for Evaluating the Effect of Wall Suction and Thermophoresis on Aerosol Particle Deposition Froma Laminar Flow over Aflat Plate,” International Communications in Heat and Mass Transfer, Vol. 26, No. 2, 1999, pp. 249-257. Hdoi:10.1016/S0735-1933(99)00011-1
- M. A. Samad and M. M. Rahman, “Thermal Radiation Interaction with Unsteady MHD Flow past a Vertical Porous Plate Immersed in a Porous Medium,” Journal of Naval Architechture and Marine Engineering, Vol. 3, No. 2, 2006, pp. 7-14.
- P. R. Nachtsheim and P. Swigert, “Satisfaction of the Asymptotic Boundary Conditions in Numerical Solution of the Systems of Non-Linear Equations of Boundary Layer Type,” Ph.D. Thesis, NASA TN D-3004, Washington DC, 1965.

