Open Journal of Applied Sciences
Vol.09 No.04(2019), Article ID:91816,13 pages
10.4236/ojapps.2019.94014
SCM Implementation Decisions of Principal-Agent under Asymmetric Information
Lina Wang1,2, Stephan Poelmans3, Koen Milis4
1Economy & Management School, Hainan Normal University, Haikou, China
2Management School, Liaoning University of Technology, Jinzhou, China
3Faculty of Economics and Management, Hogeschool-Universiteit Brussel, KULeuven Association, Brussel, Belgium
4Education Management Industry, Campus Vesta, Brussels, Belgium

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 15, 2019; Accepted: April 14, 2019; Published: April 17, 2019
ABSTRACT
The optimization investment policy decision of SCM-Supply Chain Management-implementation has been analysed under symmetric and asymmetric information conditions. For both conditions, SCM implementation options’ decision optimizing models have been developed. In these models, both clients and vendors try to pursue their own benefits. Based upon the principal-agent theory, the models show to what extent a principal (a client) needs to pay more to an agent (a vendor) in a context of asymmetric information. For the client, it is important to understand the extra costs to be able to adopt effective strategies to stimulate a vendor to perform an optimal implementation of a SCM system. The results of a simulation experiment regarding SCM implementation options illustrate and verify the theoretical findings and confirm the general notion that the less informed party is obliged to pay information rent to the better-informed party.
Keywords:
SCM Implementation Problems, Asymmetric Information, Implementation Control Cost, Evaluation Level, Principal-Agent Theory

1. Introduction
There are large similarities between the way of handling SCM implementation options and financial options, as will be demonstrated in this paper. Hence, extending financial options’ theory models can help us deal with SCM investment decisions [1] . The main idea is that several vendors are competing for the implementation rights. They can persuade the client to buy a SCM implementation in different ways. The vendor can, for example, lower his price. This action can be seen as the vendor buying a SCM implementation right option from the client. That is, during the auction, competing with other candidates, the vendor can buy the right to implement. Clients can invest in a SCM project, and grant permission to the vendor to implement. This allows both vendor and client to generate benefits from the induced investment. However, a vendor may choose not to buy the rights, but this will lead to the risk of being forced to stop his SCM activities since he is not able to implement the system he developed. Because the cost of having to stop the SCM activity is usually bigger than the cost of buying the clients’ SCM implementation rights, a vendor commonly will choose to buy the implementation rights. Therefore, the client can make the best decision policy to stimulate the vendor to give the best quality implementation of a SCM system.
The dilemma of a SCM implementation can be looked at as a problem of information asymmetry as well. It is a bottleneck problem of disturbing industries’ operations, especially of supply chain (SC) integration benefits [2] . A client, core enterprise or other member enterprise in the SC, adopts various measures to control the effect of a SCM implementation and to make sure he gets a sufficient part of the gains. But, when serious asymmetry exists between the client and the SCM vendor, a SCM implementation becomes very difficult.
As principals, clients may have different characteristics, resulting in various requirements. At the same time, the agent’s (vendor) capabilities of implementing and maintaining client-specific SCM projects may be relatively low because he doesn’t have all the information on the SCM’s real implementation effects on the client’s operation processes. On the other hand, a vendor may only care about his standard SCM implementation project, though this is possibly not suitable for the client’s business. So, there is a possible trade-off between standardization and the capability to fulfill the specific needs of the clients (customization). Moreover, clients do not necessarily have a big inside into the impact of a SCM implementation since they might not be acquainted with the possibilities and limitations of a SCM system. Often, they are not familiar with technological problems when facing a SCM implementation, while the vendors are often not acquainted with the processes and operations of the enterprise or its supply chain. Thus there is asymmetric information between client and agent.
In addition, according to the asymmetry information theory, the vendors’ private information on SCM implementations is regarded as external, and thus cannot be controlled directly by the client. It is just regarded as hidden information, causing information asymmetry. Hidden information is regarded as the first element constituting the asymmetric information theory. This is inevitably reflected in their implementation controlling actions. Given the hidden information, the vendors’ contract choices may conflict with what clients expect since the vendor is not aware of the optimal solution for the client. Thus, sub-optimal or wrong choices can be made. This is referred to as adverse choosing, the second element of information asymmetry theory. Under the condition of hidden-action, vendors are tempted to maximize solely their own benefit and opt for a generic solution to serve as many clients as possible, neglecting the specific needs of the client. One party takes advantage of the other. This is referred to as moral risk, the third element of the information asymmetry theory.
There are a lot of courtesy literatures having certain description about SCM implementation under asymmetric information. Agrell P J, et al. (2016) [3] studied the contractual choice of a coordinator to either centralize or delegate the investment decision in a three-stage chain. In the paper of Esmaeili M, et al. (2010) [4] , several seller-buyer supply chain models were proposed under an asymmetric information pattern. While in Yao D Q, et al. (2008) [5] , under certain conditions, they proved the existence of equilibrium prices and added values and so on. And, Xiao T, et al. (2008) [6] studied the coordination of a supply chain with one manufacturer and two competing retailers after the production cost of the manufacturer was disrupted.
In the paper, SCM implementation options’ decision optimizing models are established. With clients as principal, vendors as agent, SCM implementation evaluation and deviation prevention principal-agent models are proposed. In these models, both clients and vendors try to pursue their own benefits. Based upon the principal-agent theory, the models show why a principal should stimulate an agent to pursue his benefits and to what extent a situation of asymmetric information is to his disadvantage.
2. SCM Implementation Options Decision’s Principal Agent Model
As a principal, the clients’ SCM implementation benefit function, say, the principal’s target function is
(2.1)
The gains are the vendor’s offer minus the price for acquiring it, minus two parts, both indicating that the vendor’s implementation result deviates from the negotiated standard. In one part the deviation is discovered by the vendor during the process (so the price can be adjusted). If the client notices it afterwards however, it must be deducted fully from his benefits (the other part).
Here, is the client’s controlled implementation benefit.
PE is a variable that represents the probability that a client discovers deviations from the agreed implementation’s quality (described in the specifications of the contract between client and vendor) during its process. . And, we call PE as the deviation control level.
P is the SCM implementation right option. It is a decision variable, and a function of the deviation prevention level PE, .
CA is the clients cost to prevent bad implementation quality, and is a function of PA, .
PA is the evaluation level of the implementation, given by the client. It indicates whether the implementation process corresponds to the agreed specifications. PA is a function of PE, .
If PE equals 0; then PA equals 1 and W and X become irrelevant. In other words, if PA is 1, the quality is perfect and there are no inner and outer losses. PA reflects a client’s subjective judgment and .
W and X are constants that represent the vendor’s inner loss and outer loss punishments. Whereas the inner losses reflect deviations from the agreed quality (the specifications) during the implementation process (and thus are at the expense of the vendor); the outer loss refers to quality deviations, discovered after the implementation (and at the expense of the clients). i.e. the punishment for not attaining maximal quality, resp. the punishment for delivering a system that is not completely in line with the needs of the client (as specified in the contract).
The actual quality control level PA is smaller or equal to the clients’ ideal solution. So the agreed implementation level (as specified in the contract) is equal or less than A. This is a constraint of the model, which is referred to as the clients’ individual rational constraint (). According to literature [7] , the should be reformulated as follows for calculation purposes:
(2.2)
Here, a is a parameter that represents the vendors’ greatest implementation evaluation ability, and .
A vendors’ implementation controlling benefit function, that is, the agent’s target function is
(2.3)
Here, Z3 is a vendor’s implementation-controlling benefit.
is a vendor’s benefit. It is the difference between the agreed value and the real value of his solution (so the difference between the amount in the contract and the amount actually paid by the customer).
is a vendor’s benefit . It represents the client’s cost for the discovery and correction of mistakes after the implementation of the system.
UE is an agreed bonus (or premium) paid by clients in order to encourage vendors to discover and correct mistakes and avoid escalations later on.
CE is a vendor implementation evaluation cost, it is a function of PE, .
The function (Z3) consists of two major parts. The first part () represents the perfect situation: the payment for a system that attains maximum quality. Another important part represents an imperfect situation, that is, the punishment for bad quality that is recognised by the client.
In the process of a SCM implementation decision, clients must also consider their benefits. At the time period the client and vendor are actively engaged in the SCM implementation process, the client owes the vendor, and so his benefits will not be higher than the vendors’ benefits. Therefore we define, (here, b is a probability coefficient, ); whereby Z4 represents the clients’ benefits.
To calculate the clients’ benefits, we define the function Z and use Equations (2.1), (2.2) and (2.3), thus considering three elements: the client gains the Equation (2.1), the constraints of the client’s Equation (2.2) and the benefits of the vendor’s Equation (2.3).
(2.4)
3. SCM Implementation Quality Evaluation and Options Payment Decisions
In order to minimize the risks of hidden information of the vendor and get the best possible implementation evaluation level PA, especially when negotiating a SCM implementation contract, we compare two situations. The first is decision making under the assumption of symmetric information. The second situation deals with decision making under the assumption of asymmetric information (some information is hidden by the vendor).
3.1. SCM Implementation Quality Evaluation and Options Payment Decisions under the Condition of Symmetric Information
Under condition of symmetric information between clients and vendors, clients can observe the vendors’ implementation activities. Their SCM implementation decision problem is an optimization problem. The clients’ targets are: 1) to choose an appropriate quality evaluation level PA and implementation option’s payment P, and 2) to maximize the clients’ benefit function, that is:
(3.1)
At the same time, under a system based on open competition, the vendors benefits will tend towards zero, so that, , this means we can re-formulate Equation (2.3) as follows
(3.2)
Substituting Equation (3.2) into Equation (2.4), gives the following result.
In order to maximize Z, we take the first and second derivative of the function.
Taking the first derivative of PA, gives us:
The second derivative of Equation (2.4) is .
So under a condition of symmetric information, we find that:
(3.3)
The vendor’s implementation quality level and the options payment decisions are:
(3.4)
(3.5)
3.2. SCM Implementation Quality Evaluation and Options Payment Decisions under the Condition of Asymmetric Information
Now, consider the situation were vendors have SCM implementation knowledge (private information), and clients cannot obtain this information. As a result, the SCM implementation decision problem becomes an asymmetric information problem, which is a typical principal-agent problem [8] . Under these conditions, the clients’ target function can be described as shown in Equation (3.6). The clients will choose a certain implementation evaluation level PA, and an implementation option payment P to maximize the target function (2.4) under the condition of a client’s expectation, that is:
(3.6)
Here, is the clients expected target benefit function under asymmetric information. The real client’s deviation control level PE is not known exactly but is situated between an upper and lower limit; . P denotes a probability density function . And now, clients can estimate PE. This estimation is called . is a proxy for the real deviation control level, which is not yet known to the client. Clients will design a stimulus plan to obtain . This plan guides vendors to realise the deviation control level , targeted by the client [9] .
According to the proclaimed axiom of the principal-agent theory [10] , there is:
(3.7)
To maximize the target function (3.7) under condition of a client’s expectation, we take the first degree derivative of and make it zero, that is:
(3.8)
where u is the first degree derivative of implementation quality evaluation level PA to the deviation control level PE’s estimated value , and it is a newly introduced controlling variable.
(3.9)
Hence, the SCM implementation quality problem under asymmetric information can be regarded as an optimum control problem with following target functions: the benefit expectation Equation (3.6) and the maximization functions (3.8) and (3.9). We assume that under the optimum control problem we get the best possible estimate for . Through proclaiming an axiom and stimulus strategy, the deviation control level comes close to the real value. Hence, we assume that evolves towards PE. So, in the next steps the real deviation control level PE is deployed.
Using the maximum axiom to seek a solution for this classic controlling problem, we construct the following Hamilton function, based upon Equations (3.6), (3.7), (3.8):
(3.10)
Here, , are parameters, introduced to solve the problem.
To find the optimum solution, we need to maximize u, P and PA. We take partial derivatives of the Hamilton function towards each of these variables:
(3.11)
(3.12)
(3.13)
Based upon Equation (3.12), we can calculate :
(3.14)
Here, is the probability distribution function of parameter PE.
We unite Equations (3.11), (3.13) and (3.14), to get the client’s quality evaluation level under asymmetric information ():
So, to get a high quality SCM implementation under asymmetric information; we maximize PE and take its first derivative towards , i.e.,
(3.15)
4. Comparing the Implementation Results under Symmetric and Asymmetric Information Conditions
Now that we have the maximum PE under the assumption of symmetric and asymmetric information, we analyze and compare in this section the implementation evaluation level, PA, in these two situations. PA is dependent on PE, it represents the evaluation of the SCM implementation quality and it is our principal decision variable. By comparing PA in both situations and establishing whether and to what extent they differ, we can obtain the best policy to stimulate vendors to implement SCM systems optimally. In order to optimize PA we need to consider the clients implementation evaluation cost function CA as well as PA’s first and second derivatives towards CA, (which are all greater than 0). For the convenience of computation, we choose Yeom et al.’s cost function
[10] . Here, KA is a general coefficient.
From Equation (3.3)―the assumption of symmetric information―we get:
(4.1)
From Equation (3.15)―the assumption of asymmetric information―we get:
(4.2)
When we compare an implementation evaluation decision equation under symmetric information (4.1) with an implementation evaluation decision equation under asymmetric information (4.2) we find an increment, i.e.,
(4.3)
In order to further analyze the value of this increment we first consider the vendor’s benefits and bonus:
, the vendor inner loss cost, meaning a vendor’s losses when he discovers his own mistakes during the implementation;
and representing the vendors’ outer loss cost, meaning the vendor’s losses when the client discovers mistakes or deviations.
Now, suppose that the vendors’ inner loss punishment is at least equal to the inner-loss costs, , and suppose that vendors outer loss punishment is at least equal to outer loss costs, .
Using N as a constant greater or equal to 1, we can establish:
(4.4)
(4.5)
Substituting Equations (4.4), (4.5) into Equation (4.3), gives us the following result:
(4.6)
From Equation (4.6), we can know, when , , , so, . That is, when vendors’ inner loss punishment from the clients is greater than the outer loss punishment; the clients’ implementation deviation control level under asymmetric information is less than that under symmetric information. When , , so, , say, when vendors’ inner-loss punishment from clients is equal to the inner loss cost and his outer loss punishment is equal to the outer loss cost, clients implementation deviation control level under asymmetric information is equal to the results under symmetric information.
When , with X far greater than W, say , then
. Presume an implementation deviation
prevention parameter , it has a uniform distribution , get , with , so, ,
, hence, , so,
; that is, when vendors’ inner loss punishment from clients is less than the outer loss punishment, even when his outer loss punishment far exceeds the inner loss punishment, the clients implementation evaluation level under asymmetric information will not be higher than the result under symmetric information.
In sum, whether the vendors’ inner loss punishment from clients is greater or smaller than the outer loss punishment; clients’ implementation quality level decisions under asymmetric information are all lower than under symmetric information. That is because, under asymmetric information, clients cannot observe vendors’ implementation activities, the client has to do his best to lower the implementation cost, that is, the implementation deviation prevention cost.
When clients make implementation quality level decisions, the overall implementation control cost triggered includes implementation deviation control and implementation punishment costs. The mathematic equation is:
(4.7)
When , take Equation (4.1) under symmetric information and Equation (4.2) under asymmetric information into Equation (4.7), so we get:
(4.8)
Here, is the client’s implementation control cost under asymmetric information. is the client’s implementation control cost under symmetric information. Equation (4.8) shows, the clients’ implementation controlling cost under asymmetric information is higher or equal to the result under symmetric information. When , .
Consequently, when the vendor’s inner loss punishment is equal to the inner loss cost and his outer loss punishment is equal to the outer loss cost, the clients’ implementation control cost under asymmetric information is higher than the result under symmetric information. This shows that, under asymmetric information, a principal must pay the implementation control cost and should strive for an implementation agreement in which the condition of symmetric information is met as much as possible.
5. Simulation Calculations
In this section, an implementation level decision problem of a client under asymmetric information with varying deviation control levels is presented.
Suppose that the client’s achieved benefit is EUR if the vendor implements the system as agreed in the contract between vendor and client. Further presume that the client evaluated the implementation, and the vendor timely adopted implementation control measures. Under the assumption that the client has spent 1000 EUR evaluating the implementation and detecting the deviation from the agreed quality level, the client’s benefit is now EUR.
Next, consider that the client’s achieved benefit would be EUR (instead of 5000 EUR) if the vendor has the possibility to deviate from the agreed implementation quality level. The client punishes the vendor’s inner loss EUR; the outer loss punishment of the vendor is EUR.
The client’s highest implementation deviation prevention level is . In addition, , . Consider:
- The vendor’s implementation evaluation cost function to the implementation deviation prevention level PE’s first and second degree derivatives are both greater than 0;
- The client’s implementation prevention cost function to the implementation evaluation level PA’s first and second degree derivatives are both greater than 0;
- And for the convenience of dealing, choose the vendor’s evaluation cost function
, and the client’s implementation deviation prevention cost function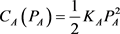 ,
, .
.
Suppose a vendor’s implementation deviation prevention coefficient, 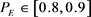 , and suppose it has a uniform distribution
, and suppose it has a uniform distribution . PE has the value of
. PE has the value of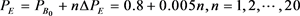 .
.
Given these calculations and assumptions, the decision results for the client are given in Figure 1 and Figure 2. In the figures, a full line represents decision results in the case of asymmetric information, whereas a dashed line represents
Figure 1. Implementation quality level strategies under symmetric and asymmetric information conditions.
Figure 2. Client’s implementation controlling cost under symmetric and asymmetric information conditions.
the results under a condition of symmetric information. Figure 1 shows that the implementation quality level, PA, under asymmetric information is lower than the quality level under symmetric information, for varying levels of PE. Figure 2 denotes that the client’s implementation control cost under asymmetric information is higher than that under symmetric information, for different levels of PE. It is thus clear that the condition of asymmetric information benefits the vendor and makes the client pay for the price of the implementation controlling cost.
6. Conclusions
In this paper, the option theory and the theory of asymmetric information were used to examine SCM implementation decisions under symmetrical and asymmetrical information conditions. In particular, SCM implementation options’ decision optimizing models were established and SCM implementation deviation prevention and evaluation principal-agent models were created. In these models, both clients (principals) and vendors (agents) try to maximize their own benefits.
Under the condition of asymmetric information, vendors hide their implementation information, which makes it a typical principal-agent problem. In this setting, the client’s target function is the subject of an optimum control problem and the clients’ targets are: 1) to choose an appropriate quality evaluation level and implementation option’s payment, and 2) to maximize the benefit function. The optimized results show the feasibility of using theories of options and asymmetric information to understand and solve SCM implementation option decisions.
The application of a simulation illustrates that the client’s required implementation quality level under asymmetric information is clearly lower than that under symmetric information. In addition, the client’s implementation control cost under asymmetric information is higher than that under symmetric information.
As a result, it is important to research the nature of hidden information and conduct further research in the development of effective clients’ strategies to optimize the level of symmetric information to avoid the risk of hidden SCM implementation costs.
Fund
This work was financially supported by the Science and Technology project of Liaoning Science and Technology Bureau of 2017; project (20170540439); the project’s name: The pollution controlling model system’s construction based on middle-micro scale.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Wang, L.N., Poelmans, S. and Milis, K. (2019) SCM Implementation Decisions of Principal-Agent under Asymmetric Information. Open Journal of Applied Sciences, 9, 159-171. https://doi.org/10.4236/ojapps.2019.94014
References
- 1. Corbett, C.J. and Groote, X.D. (2000) A Supplier’s Optimal Quantity Discount Policy under Asymmetric Information. Management Science, 46, 445-450. https://doi.org/10.1287/mnsc.46.3.444.12065
- 2. Cobett, C.J. and Tang, C.S. (2000) Designing Supply Contracts: Contract Type and Information Asymmetry. In: Tayur, S., Ganeshan, R., Michael, M., Eds., Quantitative Models for Supply Chain Management, Kluwer Academic Publishers.
- 3. Agrell, P.J. and Bogetoft, P. (2016) Decentralization Policies for Supply Chain Investments under Asymmetric Information. Managerial & Decision Economics, 38. https://doi.org/10.1002/mde.2783
- 4. Esmaeili, M. and Zeephongsekul, P. (2010) Seller-Buyer Models of Supply Chain Management with an Asymmetric Information Structure. International Journal of Production Economics, 123, 146-154. https://doi.org/10.1016/j.ijpe.2009.07.016
- 5. Yao, D.Q., Yue, X. and Liu, J. (2008) Vertical Cost Information Sharing in a Supply Chain with Value-Adding Retailers. Omega, 36, 838-851. https://doi.org/10.1016/j.omega.2006.04.003
- 6. Xiao, T. and Qi, X. (2008) Price Competition, Cost and Demand Disruptions and Coordination of a Supply Chain with One Manufacturer and Two Competing Retailers. Omega, 36, 741-753. https://doi.org/10.1016/j.omega.2006.02.008
- 7. Gaudet, G., Lasserre, P. and Van Long, N. (1998) Real Investment Decision under Adjustment Costs and Asymmetric Information. Journal of Economic Dynamics and Control, 23, 71-95. https://doi.org/10.1016/S0165-1889(97)00107-3
- 8. Yuan, H.X. and Tian, Z.X. (2003) Material Options Optimum Investment Problem Research under Asymmetric Information. Management Science Journal, 6, 28-33.
- 9. Tsay, A. and Nahmias, S. (2000) Modeling Supply Chain Contracts: A Review. In: Tayur, S., Ganeshan, R., Michael, M., Eds., Quantitative Models for Supply Chain Management, Kluwer Academic Publishers, Boston.
- 10. Yeom, S., Blachandran, K. and Ronen, J. (2000) The Role of Transfer Price for Coordination and Control within a Firm. Review of Quantitative Finance and Accounting, 14, 161-192. https://doi.org/10.1023/A:1008355713528



