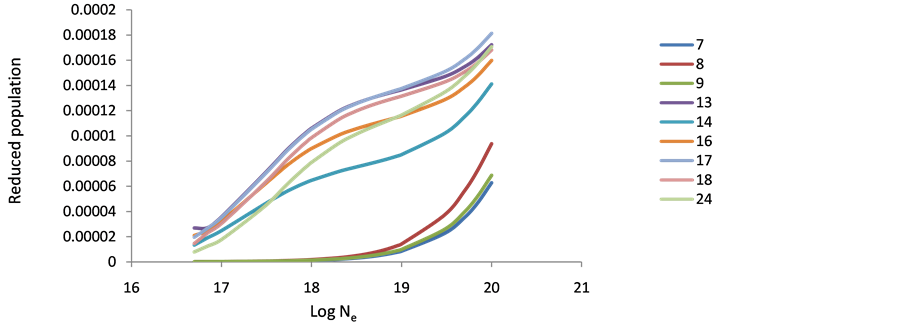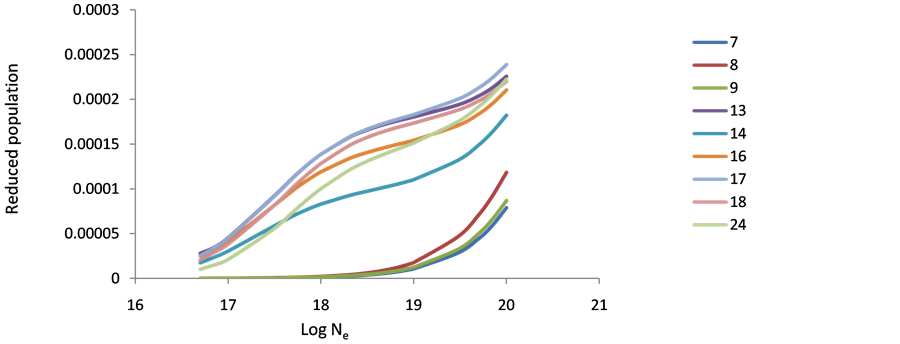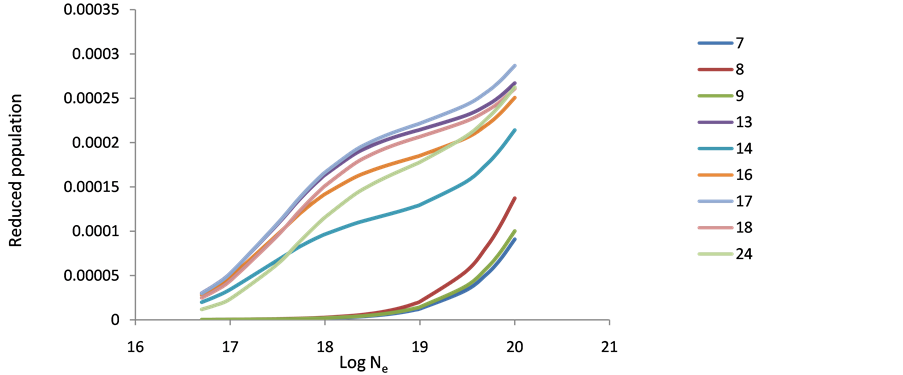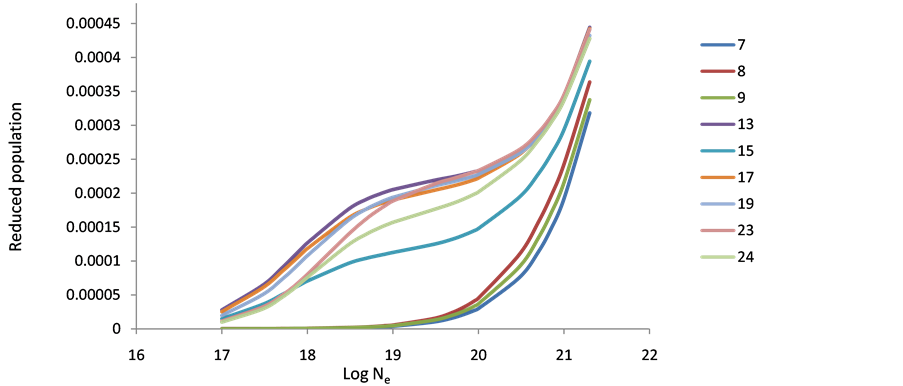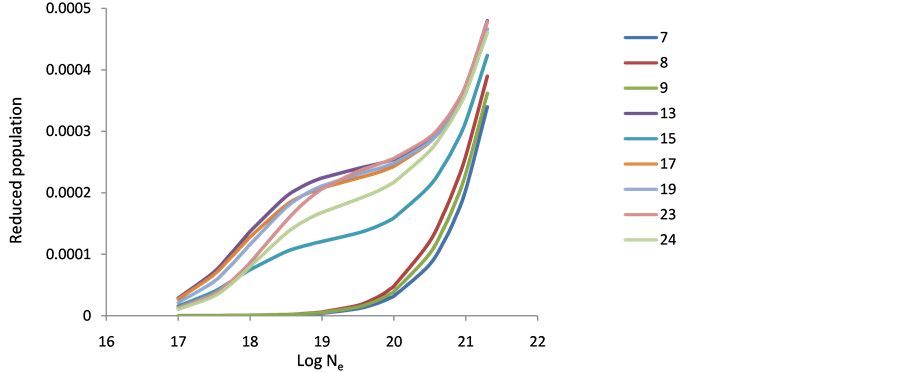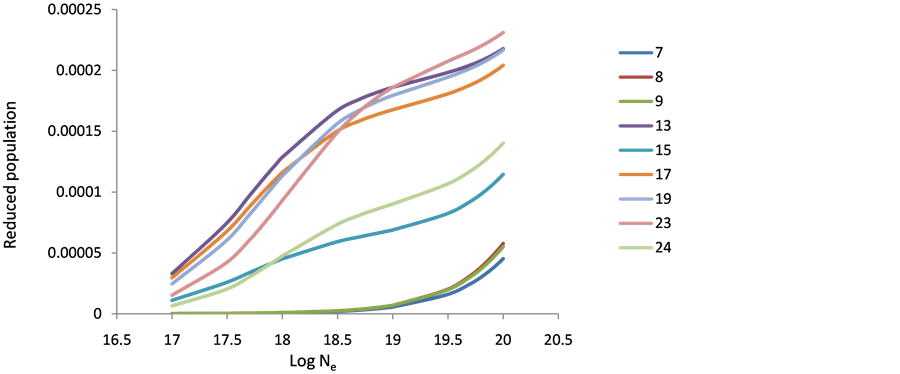Open Journal of Applied Sciences
Vol.06 No.04(2016), Article ID:65532,17 pages
10.4236/ojapps.2016.64023
Theoretical Study of Laser Emission for C-Like (Ar XIII), (Ti XVII) and (Fe XXI)
Wessameldin S. Abdelaziz1, Th. M. El Sherbeni2, Nahed H. Wahba1
1National Institute of Laser Enhanced Sciences, Cairo University, Giza, Egypt
2Laser and New Materials Laboratory, Physics Department, Faculty of Science, Cairo University, Giza, Egypt

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 March 2016; accepted 12 April 2016; published 15 April 2016
ABSTRACT
Energy levels, transition probability and oscillator strengths have been calculated for the Ar XIII, Ti XVII and Fe XXI. The configurations included in the calculations are 2s2 2p2, 2s2 2p 3l (l = s, p & d) and 4l (l = s, p, d, & f) of C-like Ar XIII, Ti XVII & Fe XXI which has 69 fine structures by using the fully relativistic flexible atomic code (FAC) program. These data are used in the determination of the reduced population and gain coefficients over a wide range of electron densities from (10+18 to 10+23) and at various plasmas temperatures. The results show that the transitions in Ar18+, Ti22+, and Fe26+ ions are the most promising laser emission lines in the XUV and soft X-ray spectral regions.
Keywords:
XUV, Soft X-Ray, Laser Radiation, Population Inversion, Gain Coefficient

1. Introduction
The last three decades enormous advances in our understanding and developing high-efficiency of X-ray laser with gain [1] [2] by using the mechanism for demonstrating X-ray lasing in resonant photo pumping have been seen. The pump power needed to achieve inversion was extremely high. (ECP) electron collisional pumping has been the most familiar and suitable pumping mechanisms used in soft X-ray lasers [3] . The modeling of astrophysical and laboratory plasmas used c-like ions and their emission lines. Those data for transition mostly lie in the soft X-ray and EUV regions [4] . Energy levels, spontaneous decay rates and oscillator strengths have been calculated by Aggrawal et al. [5] [6] , Feldman et al. [7] & Aggrawal et al. [8] for transitions in Ar XIII, Ti XVII & Fe XXI. But no much work has been done to predict the gain of C-like Ar XIII, Ti XVII & Fe XXI theoretically.
In this paper, we calculate energy levels for 69 fine-structure states using a fully relativistic approach based on Dirac equation. Weighted oscillator strengths, spontaneous radiative decay rates are calculated in the single multipole approximation, and collision strengths by electron impact using the factorization-interpolation method are calculated in the distorted wave approximation. Effective collision strengths are calculated by interpolating the data from the collision strengths and integrating over Maxwellian distribution at different temperatures. Rate coefficients are calculated from effective collision strengths using a formula that will be described later in this paper. Then, we predict the reduced population and gain coefficient for C-like Ar XIII, Ti XVII & Fe XXI by a steady state equation in the collisional radiative model after achieving a population inversion between the allowed transition states.
2. Computation of Gain Coefficient
The possibility of laser emission from plasma of Ar XIII, Ti XVII and Fe XXI ions via electron collisional pumping, in the XUV spectral region was investigated at different plasma temperatures and electron densities.
The reduced population densities were calculated by solving the coupled rate equations [7] - [10] .
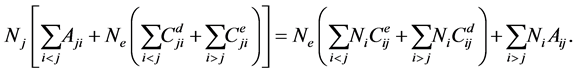 (1)
(1)
where 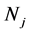 and
and 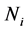 is the fractional population of level respectively,
is the fractional population of level respectively, 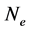 is the electron density,
is the electron density, 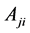 is the Einstein coefficient for spontaneous radiative decay from j to i; and
is the Einstein coefficient for spontaneous radiative decay from j to i; and 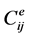 and
and 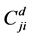 represent the rate coefficient for collisional excitation and de-excitation respectively. The actual population density
represent the rate coefficient for collisional excitation and de-excitation respectively. The actual population density 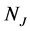 of the
of the 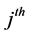 level can be calculated from the equation of identity [11] [12] .
level can be calculated from the equation of identity [11] [12] .
 (2)
(2)
where 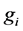 and
and 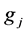 are the statistical weights of the lower and upper levels, respectively.
are the statistical weights of the lower and upper levels, respectively.
The electron impact excitation rates usually are expressed via the effective collision strengths 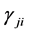 as
as
 (3)
(3)
where the values of 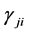 and
and 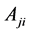
The actual population density 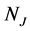
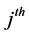
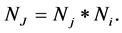
where 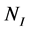
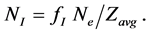
where 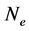
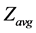
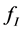
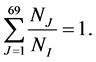
After the calculation of levels population density, the quantities 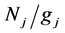
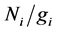
Once a population inversion has been ensured a positive gain through F > 0 [13] is obtained by
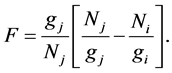
where 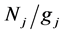
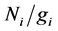
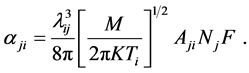
where M is the ion mass 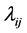
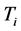
3. Results and Discussions
3.1. Energy Levels
By using the fully relativistic flexible atomic code (FAC) [14] we obtained energy level values for the 1s2 2s2 2pnl (n = 3, l = s, p & d) and ml (m = 4, l = s, p, d & f) configurations in C-like Ar18+, Ti22+ and Fe26+ ions. This data presented in Tables 1-3. The first column of each table provides an index for the levels, the second column presented the main components of the computed eigenvectors and the third column presented our calculations of energy levels. Tables 4-6 presented the comparing data between our calculations and with the experimental values compiled by NIST. We obtained the agreement between FAC, Bhatia, Seely and Feldman [15] for Ar18+, Ti22+ and Fe26+ energy levels and with the other experimental energies [16] [17] with the values available at the National Institute of Standards and Technology (NIST) [18] and is within values less than 0.5% for a majority of levels.
3.2. Level Population
The reduced population densities are calculated for 69 fine structure levels arising from 1s2 2s2 2pnl (n = 3, l = s, p & d) and ml (m = 4, l = s, p, d & f) configurations that emit radiation in the XUV and soft X-ray spectral regions. The calculations were performed by solving the coupled rate Equation (1) simultaneously using MAT- LAB version 7.10.0 (R2010a) computer program. The reduced populations density are calculated as a function of electron densities and plotted at different plasma temperatures for Ar18+, Ti22+ and Fe26+ ions.
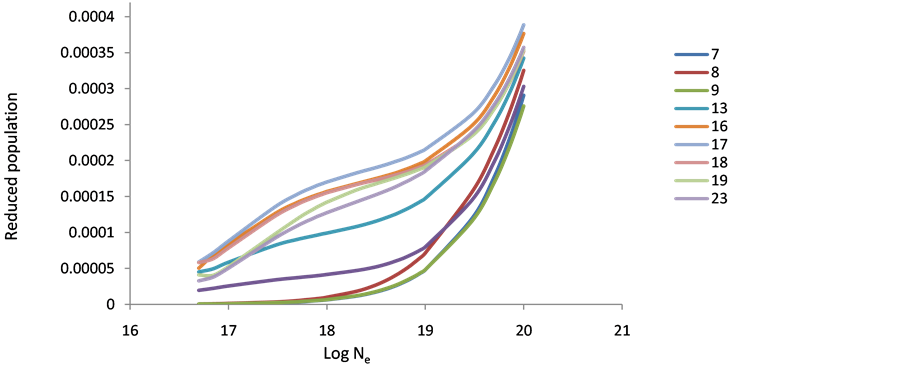
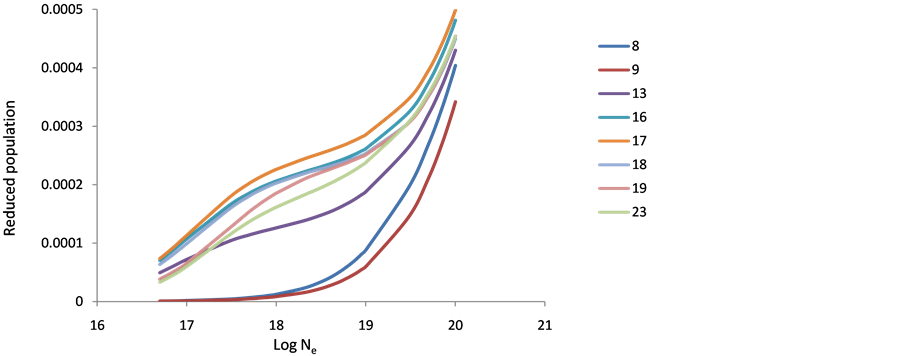
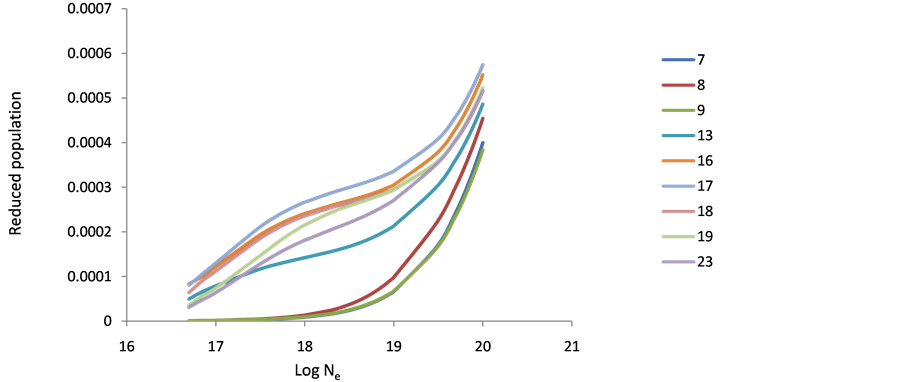
The behavior of level populations density of the various ions (Ar XIII, Ti XVII & Fe XXI) can be explained as follows: in general, at low electron densities the reduced population density is proportional to the electron density, where excitation to an excited state is followed immediately by radiation decay, and collisional mixing of excited levels can be ignored. This result is in agreement with that of Feldman et al. [9] [10] [19] . At high population densities (10+23), radiative decay to all levels will be negligible compared to collisional depopulations and all level populations become independent of electron density and are approximately equal. The 10+17 electron density shows a peak at before the other levels then decreases to the saturation faster than the other levels, which mean that then on radiative transitions dominant the de-excitation because of its higher energy and fast decay time (see Figures 1-9). The population inversion is largest where electron collisional de-excitation rate for the upper level is comparable to radiative decay for this level [9] [19] .
3.3. Inversion Factor
Laser amplification will occur only if there is population inversion, or in other words, for positive inversion factor F > 0. In order to work in the XUV and X-ray spectral regions, we have selecting transitions between any two levels producing photons with wavelengths between 5˚ and 100˚A. The electron density at which the population reaches corona equilibrium approximately equals to A/D, where A is the radiative decay rate and D is the collisional de-excitation rate [13] . The population inversion is largest where the electron collisional de-excita- tion rate for the upper level is comparable to the radiative decay rate for this level.
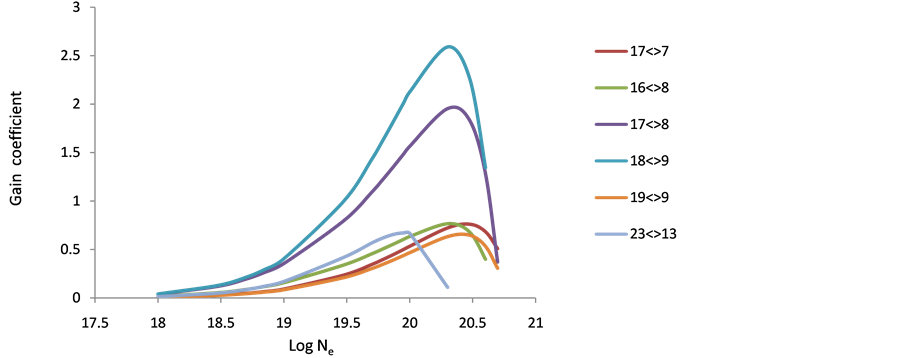
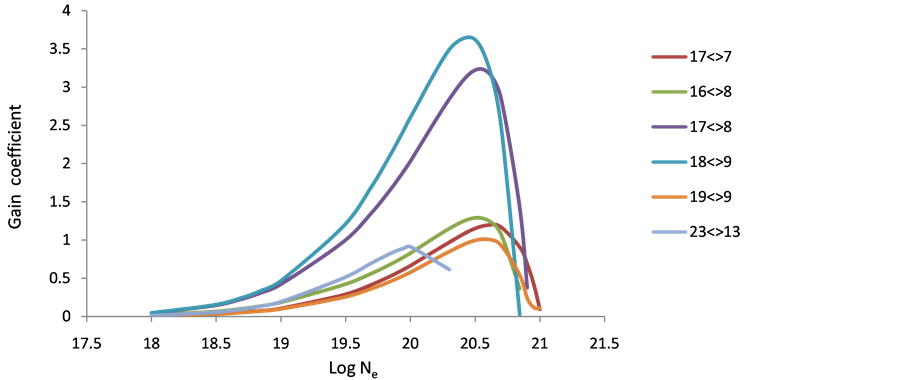
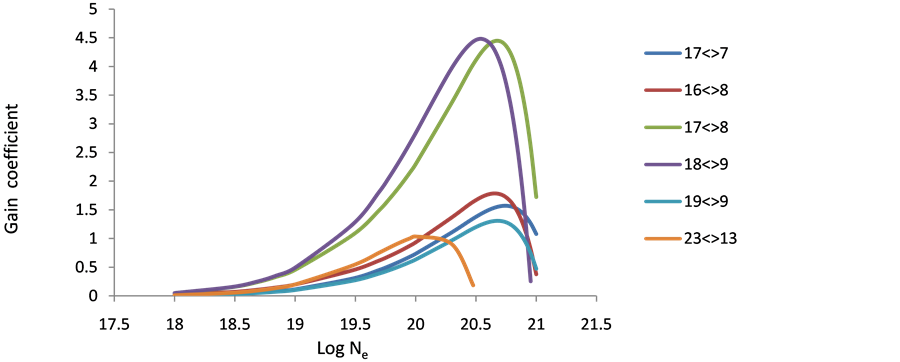
3.4. Gain Coefficient
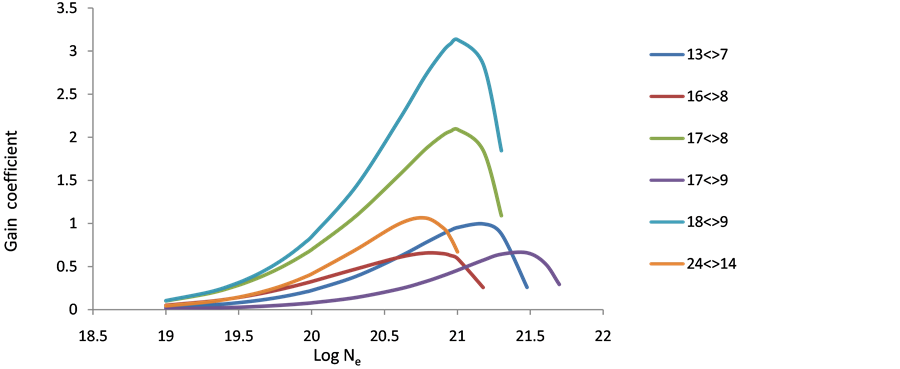
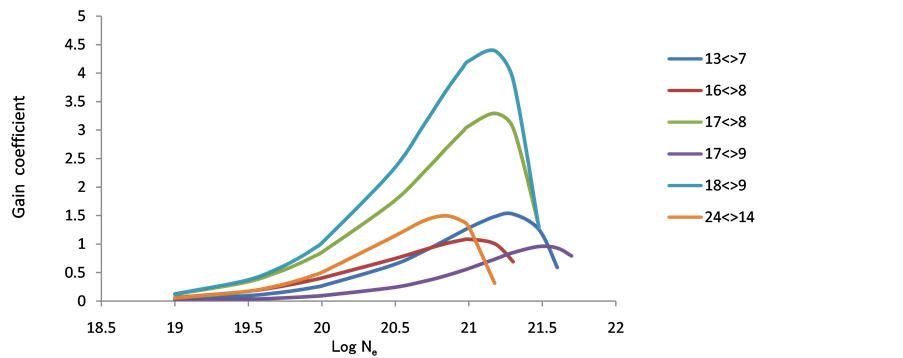
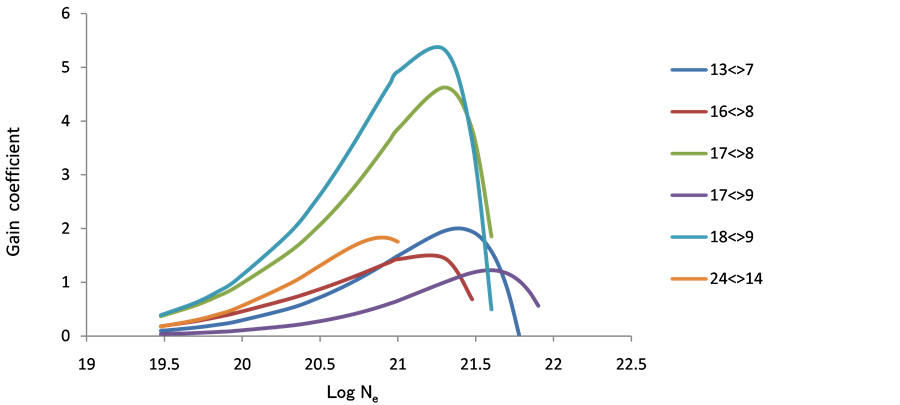
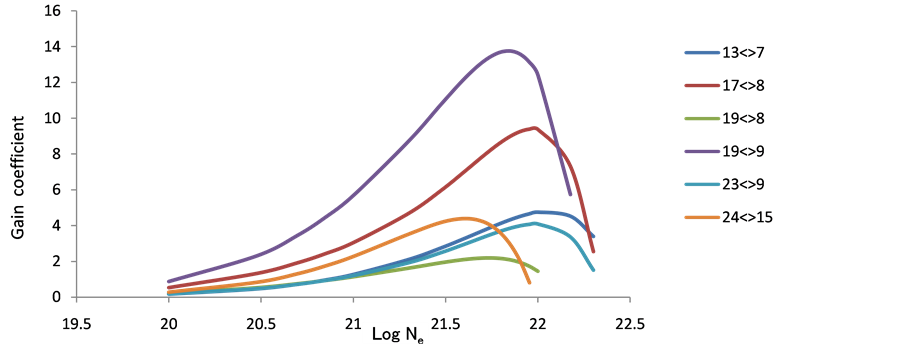
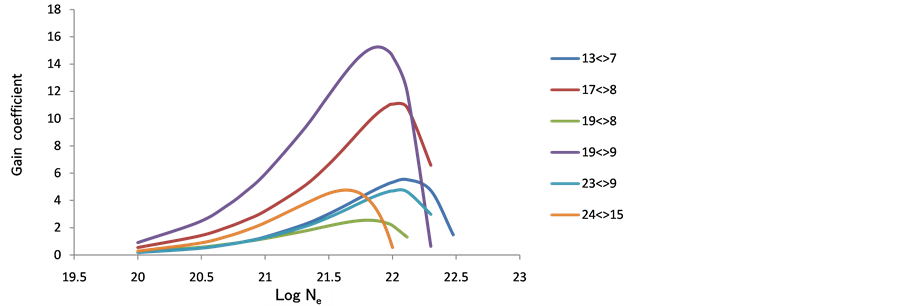
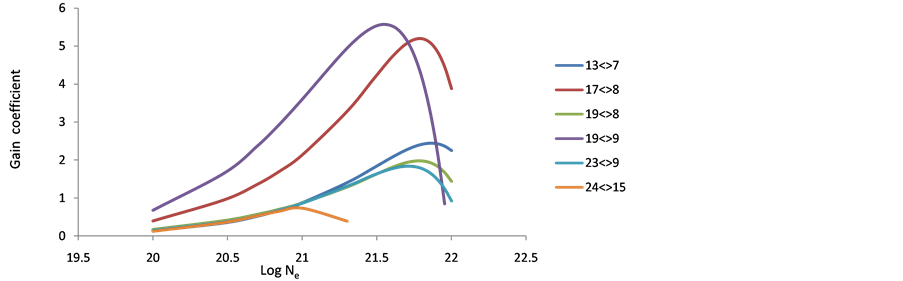
As population inversion will be positive in laser medium. Equation (8) has been used to calculate gain coefficient for the Doppler broadening of various transitions in the Ar XIII, Ti XVII & Fe XXI ions. For F > 0 transition having positive inversion with the maximum gain coefficient in cm−1. The maximum gain was calculated and plotted against electron density Figures 10-18 these short wavelength laser transitions can be produced using plasmas created by optical lasers as the lasing medium.
For Ar XIII, Ti XVII & Fe XXI ions the rates for electron collisional excitation from the 1s2 2s2 2p2 ground
Table 1. State definitions and energy levels for Ar XIII.
Table 2. State definitions and energy levels for (Ti XVII).
Table 3. State definitions and energy levels for Fe XXI.
Table 4. Comparison between some energy levels for Ar XIII.
Note: (a) NIST [18] data; (b) CIV3 program by K. M. Aggarwal [5] (c) SS. The data from the work done by Bhatia et al. [15] & (d) Our calculations calculated by the fully relativistic flexible atomic code (FAC).
state to the 1s2 2s2 2p 3l (l = s, p, d) configuration are greater than the rates for excitation from the ground state to the 1s2 2s2 2p 4l state. For electron densities and electron temperatures that are typical of laboratory high- density plasma sources this agreement with Feldman et al. [9] , such as laser-produced plasmas, it is possible to create a quasi-stationary population inversion in this ion.
Under favorable conditions large laser gains for this transition in the XUV and soft X-ray regions of the spectrum can be achieved in the carbon-like Ar XIII, Ti XVII & Fe XXI ions from our calculation. The gain calculations were performed at various electron temperatures and at various electron densities. It is obvious that the gain increases with the temperature.
Table 5. Comparison between some energy levels for Ti XVII.
Note: (a) NIST [18] data, (b) GRASP code by K. M. Aggarwal [4] (c) SS. The data from the work done by Bhatia et al. [15] & (d) Our calculations calculated by the fully relativistic flexible atomic code (FAC).
The results have suggested the following laser transitions in the Ar XIII, Ti XVII & Fe XXI plasma ions, wavelength, radiative life time of the upper and lower laser levels in the possible laser transitions and maximum gain coefficient at various temperatures presented in Tables 7-9, as the most promising laser emission lines in the XUV and soft X-ray spectral regions.
3.5. Radiative Life Time
The lifetimes are determined almost entirely from the allowed and the strong inter combination transitions. The radiative lifetime 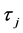
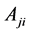
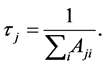
where the sum is extended over all the lower states which can be reached from the upper state by radiative decay.
Table 6. Comparison between some energy levels for Fe XXI.
Note: (a) NIST [18] data, (b) GRASP code by K. M. Aggarwal [20] (c) SS. The data from the work done by Bhatia et al. [15] . (d) Our calculations calculated by the fully relativistic flexible atomic code (FAC).
Figure 1. Reduced population of Ar+16 levels after electron collisional pumping as a function of the electron density at temperature 300 eV.
Figure 2. Reduced population of Ar+18 levels after electron collisional pumping as a function of the electron density at temperature 400 eV.
Figure 3. Reduced population of Ar+18 levels after electron collisional pumping as a function of the electron density at temperature 500 eV.
Figure 4. Reduced population of Ti+22 levels after electron collisional pumping as a function of the electron density at temperature 400 eV.
Figure 5. Reduced population of Ti+22 levels after electron collisional pumping as a function of the electron density at temperature 500 eV.
Figure 6. Reduced population of Ti+22 levels after electron collisional pumping as a function of the electron density at temperature 600 eV.
Figure 7. Reduced population of Fe+26 levels after electron collisional pumping as a function of the electron density at temperature 900 eV.
Figure 8. Reduced population of Fe+26 levels after electron collisional pumping as a function of the electron density at temperature 1000 eV.
Figure 9. Reduced population of Fe+26 levels after electron collisional pumping as a function of the electron density at temperature 1100 eV.
Figure 10. Gain coefficient of possible laser transition against electron density at temperaturev300 eV in Ar+18.
Figure 11. Gain coefficient of possible laser transition against electron density at temperature 400 eV in Ar+18.
Figure 12. Gain coefficient of possible laser transition against electron density at temperature 500 eV in Ar+18.
Figure 13. Gain coefficient of possible laser transition against electron density at temperature 400 eV in Ti+2.
Figure 14. Gain coefficient of possible laser transition against electron density at temperature 500 eV in Ti+22.
Figure 15. Gain coefficient of possible laser transition against electron density at temperature 600 eV in Ti+22.
Figure 16. Gain coefficient of possible laser transition against electron density at temperature 900 eV in Fe+26.
Figure 17. Gain coefficient of possible laser transition against electron density at temperature 1000 eV in Fe+26.
Figure 18. Gain coefficient of possible laser transition against electron density at temperature 1100 eV in Fe+26.
Table 7. Laser transitions, wavelength, radiative life time of the upper and lower laser levels in the possible laser transitions and maximum gain coefficient at temperatures (300, 400 and 500) eV in the possible laser transitions. (Ar XIII)
Table 8. Laser transitions, wavelength, radiative life time of the upper and lower laser levels in the possible laser transitions and maximum gain coefficient at temperatures (400, 500, and 600) eV in the possible laser transitions. (Ti XVII)
Table 9. Laser transitions, wavelength, radiative life time of the upper and lower laser levels in the possible laser transitions and maximum gain coefficient at temperatures (900, 1000 and 1100) eV in the possible laser transitions. (Fe XXI)
Tables 7-9 contains the present results of radiative lifetime for the upper and lower laser levels for the (Ar XIII), (Ti XVII) and (Fe XXI).
4. Conclusion
In this work the analysis that has been presented shows that electron collisional pumping (ECP) is suitable for attaining population inversion and offers the potential for laser emission in the spectral region between 30 and 111˚A from the Ar XIII, Ti XVII & Fe XXI ions. This class of lasers can be achieved under the suitable conditions of pumping power as well as electron density. If the positive gains obtained previously for some transitions in the ions under studies (Ar XIII, Ti XVII & Fe XXI ions) together with the calculated parameters could be achieved experimentally, then successful low-cost electron collisional pumping XUV and soft X-ray lasers can be developed for various applications, and the most promising laser emission lines in the XUV and soft X-ray spectral regions.
Acknowledgements
I would like to express my sincere thanks to Mr. Ahmed. Gab Allah for their encouragement and support.
Cite this paper
Wessameldin S. Abdelaziz,Th. M. El Sherbeni,Nahed H. Wahba, (2016) Theoretical Study of Laser Emission for C-Like (Ar XIII), (Ti XVII) and (Fe XXI). Open Journal of Applied Sciences,06,217-233. doi: 10.4236/ojapps.2016.64023
References
- 1. Vinogradov, A.V., Sobelmen, I.I. and Yukov, E.A. (1975) Possibility of Constructing Afar-Ultraviolet Laser Utilizing Transitions in Multiply Charged Ions in an Inhomogeneous Plasma. Soviet Journal of Quantum Electronics, 5, 59. http://dx.doi.org/10.1070/QE1975v005n01ABEH010704
- 2. Norton, B.A. and Peacock, N.J. (1975) Population Inversion in Laser-Produced Plasmas by Pumping with Opacity- Broadened Lines. Journal of Physics B, 8, 989-996. http://dx.doi.org/10.1088/0022-3700/8/6/026
- 3. Eliezer, S. and Mima, K. (2009) Applications of Laser-Plasma Interactions. Taylor & Francis,
- 4. Aggarwal, K., Keenan, F. and Msezane, A. (2003) Oscillator Strengths for Transitions in C-Like Ions between KXIV and MnXX. The Astronomy and Astrophysical Journal, 401, 377-383.
- 5. Aggarwal, K., Keenan, F. and Msezane, A. (2001) Oscillator Strengths for Transitions in C-Like Ions between FIV and ArXIII. Journal Supplement, 136, 763-787.
- 6. Aggarwal, K., Hibbert, A., Keenan, F. and Norrington, P. (1997) Oscillator Strengths for Transitions in CaXV and FeXXI. Journal of Astrophysical, 108, 575-590. http://dx.doi.org/10.1086/312967
- 7. Feldman, U., Bhatia, A.K. and Suckewer, S. (1983) Short Wavelength Laser Calculations for Electron Pumping in Ne- Lie Kr (Kr XXVII). Journal of Applied Physics, 45, 2188-2197. http://dx.doi.org/10.1063/1.332371
- 8. Feldman, U., Seely, J.F. and Doschek, G.A. (1986) 3S-3P Laser Gain and X-Ray Line Ratios for the Carbon Isoelectronic Sequence. Journal of Applied Physics, 59, 3953-3957. http://dx.doi.org/10.1063/1.336695
- 9. Feldman, U., Doschek, G.A., Seely, J.F. and Bhatia, A.K. (1985) Short Wavelength Laser Calculation for Electron Pumping in BeI and BI Isoelectronic Sequences (18 ≤ Z ≥ 36). Journal of Applied Physics, 58, 2909. http://dx.doi.org/10.1063/1.335838
- 10. Feldman, U., Seely, J.F. and Bhatia, A.K. (1984) Scaling of Collisional Pumped 3S-3P Lasers in the Neon Isoelectronic Sequence. Journal of Applied Physics, 56, 2475-2478. http://dx.doi.org/10.1063/1.334308
- 11. Goldstein, W.H., Oreg, J., Zigler, A. and Klapisch, M. (1988) Gain Prediction for Nickel-Like Gadolinum from a 181-Level Multiconfigurational Distorted-Wave Collisional-Radiative Model. Physical Review A, 38, 1797-1804.
- 12. Vinogradov, A.V. and Shleyaptsev, V.N. (1980) Calculation of Population Inversion Due to Transitions in Multiply Charged Neon-Lie Ions in the 200-2000 A Range. Soviet Journal of Quantum Electron, 10, 754. http://dx.doi.org/10.1070/QE1980v010n06ABEH010287
- 13. Sobel’man, I.I. (1979) Introduction to the Theory of Atomic Spectra, International Series of Monographs in Natural Philosophy. Vol. 40, Pergamon Press, Oxford.
- 14. FAC Code. http://kipac-tree.stanford.edu/fac
- 15. Bhatia, A.K., Seely, J.F. and Feldman, U. (1987) Atomic Data and Spectral Line Intensities for the Carbon Iso Electronic Sequence (ArXIII through KrXXXI). Atomic Data and Nuclear Data Tables, 36, 453-494. http://dx.doi.org/10.1016/0092-640X(87)90012-X
- 16. Hibbert, A., Ledourneuf, M. and Mohan, M. (1993) Energies, Oscillators Strengths, and Life Times for Neon-Like Ions up to Kr XXVII23-112 ADNDT. Atomic Data and Nuclear Data Tables, 53, 23-112.
- 17. Yuan, G., Kato, Y., Daido, H., Kodama, R. and Murai, K. (1996) Accurate Wavelength Determination of the Lasing and Nonlasing Lines in Laser-Produced Germanium Plasma. Physica Scripta, 53, 197-203.
- 18. NIST. http://physics.nist.gov/phys Ref Data/ASD/Levels_form.html
- 19. Feldman, U., Seely, J.F. and Bhatia, A.K. (1985) Density Sensitive X-Ray Line Ratios in the BeI, BI, and NeI Isoelectronic Sequences. Journal of Applied Physics, 58, 3954-3958. http://dx.doi.org/10.1063/1.335569
- 20. Aggarwal, K.M., Hibbert, A., Keenan, F.P. and Norrington, P.H. (1997) Oscillator Strengths for Transitions in CaXV and FeXXI. The Astrophysical Journal Supplement Series, 108, 575è590.