Open Journal of Applied Sciences
Vol.05 No.10(2015), Article ID:60451,9 pages
10.4236/ojapps.2015.510056
Knowledge Discovery from Dynamic Data on a Nonlinear System
Chen-Sung Chang
Department of Information Management, Nan-Kai University of Technology, Taiwan
Email: cschang@nkut.edu.tw
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 September 2015; accepted 18 October 2015; published 21 October 2015
ABSTRACT
A method is presented for performing knowledge discovery on the dynamic data of a nonlinear system. In the proposed approach, a synchronized phasor measurement technique is used to acquire the dynamic data of the nonlinear system and a hyper-rectangular type neural network (HRTNN) is then applied to extract crisp and fuzzy rules with which to estimate the system stability. The effectiveness of the proposed methodology is verified using the dynamic data of a typical real-world nonlinear system, namely an AEP-14 bus, and the extracted rules are relating to the knowledge discovery of the stability levels for the nonlinear system. The discovered relationships among the dynamic data (i.e., the operating state), the extracted rules, and the system stability are confirmed by means of a two-stage confirmatory factor analysis.
Keywords:
Knowledge Discovery, Synchronized Phasor Measurement, Hyper-Rectangular Type Neural Network (HRTNN), Structural Equation Modeling (SEM), Confirmatory Factor Analysis

1. Introduction
The knowledge discovery and data mining filed draws on findings from statistics, databases, and artificial intelligence to construct tools that let we gain insight and useful information from massive data sets [1] -[3] . People in business, medicine and government collect such data sets, and several commercial packages provide for knowledge discovery tools [4] - [8] . But these general knowledge discovery systems are unable to be qualified, during real-time knowledge discovery from dynamic data of on-line systems.
The ability to rapidly acquire synchronized phasor measurements from around the system opens up new practical possibilities for knowledge discovery and data mining. Therefore, a methodology of knowledge discovery using the dynamic data as inputs, acquired by synchronized phasor measurements is proposed. The synchronized phasor measurements provide a method for comparing phase and sequence values from anywhere on a dynamic system [9] [10] . The method of collecting and using this information impacts communications and data processing requirements. These requirements can vary from a serial cable and hand-held calculator to a 1 Gbps Ethernet network with multi-tiered data concentrators and server [11] [12] . With the advent of Global Positioning System (GPS) [13] , the synchronized sampling signals are available in modern workstations. Utilities can use PMUs (Phasor Measurement Units) to get the simultaneous Phasor in various data of dynamic system at common time base provided by GPS.
In the current text, the knowledge discovery of nonlinear system is generally formulated as a classification problem. In general, classification problems can be solved either exclusively or non-exclusively. In the former approach, a set of objects is partitioned crisply such that each object belongs to one class and to one class only. By contrast, in non-exclusive or overlapping classification techniques, an object can be assigned to one or more classes. Fuzzy classification is a particular form of non-exclusive classification in which each pattern is assigned a certain degree of belongingness (i.e. membership) to every class within a partition. In other words, the decision boundaries demarcating the various classes are vague. Therefore, when developing knowledge discovery systems, a major concern is the construction of appropriate fuzzy classifiers. Generally speaking, these classifiers are constructed using some forms of knowledge-based approach. Typically, such approaches commence by establishing a fuzzy partition of the pattern space and then developing appropriate fuzzy rules for each fuzzy subspace. The classification ability of knowledge discovery systems based on fuzzy rules is largely dependent upon the number of partitions within each feature. Therefore, a more appealing, albeit somewhat complicated, method has been proposed for extracting fuzzy rules directly from numerical data [14] . In [15] and [16] , the authors proposed techniques for extracting fuzzy rules corresponding to specific fuzzy regions as a means of solving classification problems. In [17] , the authors presented a method for extracting crisp classification rules directly from numerical data by applying a hyper rectangular composite neural network (HRCNN) trained by a supervised decision-directed learning (SDDL) algorithm.
The purpose of this paper is not only to extract the rules of nonlinear dynamical system, but also to discover a knowledge-base model in which causal relationships among the different state variables are adequately established. The starting point was the extracted fuzzy rules redesign of a structural model, where the knowledge discoveries were identified. These fuzzy rules will be included in a general model to highlight the relationship among the different state variables. The appropriate methodology to perform this task is structural equation modeling (SEM).
SEM grows out of, and serves purposes similar to multiple regression, but in a more powerful way. SEM allows modeling of the relationships between multiple independent and dependent variables simultaneously, and SEM has the advantage of dissecting these relationships, assessing the total effects of variables on one another. Additionally, SEM provides the associations between variables and estimates the strengths of these relationships in an integrated model [18] . The principle adopted by SEM is based on determining model parameters so as to replicate in the best possible manner the covariance matrix of the dimensions in the model system. This approach facilitates the estimation of complex model systems, determining causal relationships among a set of dimensions, which may include ordinal response variables as well as continuous measurements [19] . SEM has been successfully used in several disciplines including, for example, sociology, psychology, marketing [20] or educational sciences [21] . In this paper, SEM has been applied to develop acceptance models to confirm the knowledge discovery from dynamic data.
The current study proposes a synchronized phasor measurement technique to acquire the dynamic data of nonlinear system, and using the hyper rectangular type’s neural networks to extract the fuzzy rules from the dynamic data. A reasonable structural equation modeling confirms the rules extracted by a trained HRTNN from dynamic system data eventually. The remainder of this paper is organized as follows: Section 2 describes the dynamic data acquisition process performed using synchronized PMUs; Section 3 describes the fuzzy rule extraction procedure and presents the architecture of the FHRCNN; Section 4 develops the concept SEM to confirm the knowledge discovery; Section 5 evaluates the performance of the proposed methodology via its application to a real-life system (AEP-14 bus system) under various operating conditions; Finally, Section 6 summarizes the major contributions of the current study and provides some brief concluding remarks.
2. Dynamic Data Acquisition for Nonlinear System
2.1. Nonlinear System Model
Consider a nonlinear dynamic system described by
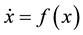 (1)
(1)
where 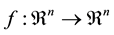 is assumed to satisfy the necessary conditions for the existence and uniqueness of the solutions, and
is assumed to satisfy the necessary conditions for the existence and uniqueness of the solutions, and 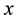 is a state vector. Nonlinear dynamic systems generally vary with time. As a result,
is a state vector. Nonlinear dynamic systems generally vary with time. As a result, 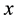 is a function of time
is a function of time 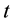 and Equation (1) may thus be regarded as a differential equation parameterized by a single parameter, namely
and Equation (1) may thus be regarded as a differential equation parameterized by a single parameter, namely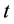 . That is, mass or periods when they are part of a sentence, as in
. That is, mass or periods when they are part of a sentence, as in
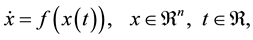 (2)
(2)
where 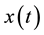 is an n-dimensional state vector.
is an n-dimensional state vector.
2.2. Dynamic Data Acquisition Using Synchronized Phasor Measurement Units
Coupling time-synchronizing techniques with computer-based measurement methods enables the measurement of dynamic information on a real-time basis, and makes possible automatic knowledge discovery on dynamic data. The most common synchronized phasor measurement techniques are well documented in [9] and [10] . Hence, the present study provides no more than a brief outline of their role in the acquisition of the dynamic data associated with a nonlinear system.
In general, a phasor is a complex number used to represent a sinusoidal function of time for a nonlinear system. For convenience, when calculating the state vector  of the system using phasor data, the phasor magnitude is set equal to the rms value of the sinusoidal waveform. In general, a sinusoidal quantity can be defined as follows:
of the system using phasor data, the phasor magnitude is set equal to the rms value of the sinusoidal waveform. In general, a sinusoidal quantity can be defined as follows:
 (3)
(3)
However, a phasor can only represent a single-frequency sinusoidal function, and therefore the phasor representation cannot be directly applied for dynamic data acquisition purposes. However, the general concept of phasors can still be used to represent data corresponding to more complex signals. For example, assume that sample data 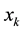 is obtained from signal
is obtained from signal  over one complete period of the waveform (with
over one complete period of the waveform (with 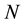 samples taken each period). The corresponding phasor can be expressed as
samples taken each period). The corresponding phasor can be expressed as
 (4)
(4)
where the sampling frequency is . Then, defining
. Then, defining  as the sampling angle
as the sampling angle

However, while the state of a nonlinear system can be expressed in terms of phasors, if several phasors are to be measured simultaneously they must be measured using a common time base. Accordingly, many Phasor Measurement Units (PMUs) triggered by synchronization signals received from GPS satellite systems have been developed and are now commercially available. In the proposed dynamic data acquisition for nonlinear system approach, 
3. Fuzzy Rule Extraction Using Hyper-Rectangular Type Neural Network
3.1. Crisp Rule Extraction
The construction of a rule-based system inevitably involves the process of acquiring if-then rules, irrespective of whether the system consists of crisp rules or fuzzy rules [14] . The most straightforward means of obtaining these rules is simply to ask human experts. However, the difficulties involved in establishing an all-embracing set of rules based on the information received from such experts are well known [15] - [17] . Therefore, a hyper rectangular type’s neural network was applied as a means of extracting crisp rules directly from the dynamic data generated by the nonlinear system of interest. In such networks, the neural nodes can be described using the following set of equations:



where

Note that 




with a value of less than 1; 



Furthermore, from Equations (6)-(10), it can be shown that the crisp classification knowledge can be described in the form of the following production rule:
IF 

The domain defined by the antecedent of Equation (11) is a hyper-rectangle of the form 




IF

IF 

ELSE

Note that the 


3.2. Fuzzy Rule Extraction
The aim of the crisp classification approach described above is to estimate an exact boundary inside which all of the patterns belonging to the same class lie. However, intuitively, it is inappropriate to apply crisp classification rules to knowledge discovery schemes for nonlinear systems, which are inherently fuzzy rather than precise in nature. Consequently, the current study develops a specific-to-purpose membership function to transform the crisp classification rules extracted by the HRTNN into fuzzy equivalents. In contrast to crisp classification rules, fuzzy classification rules regard the decision boundary between two different classes as grey rather than black and white. Patterns falling within this grey region are assigned a partial membership value representing the degree to which they belong to each class. In conventional fuzzy rule partitions, the membership functions are generally assumed to be triangular, trapezoidal or bell-shaped. However, no systematic methods are currently available for choosing appropriate membership functions, and as a result, the processes of establishing an appropriate number of divisions of the inputs and developing suitable membership functions, respectively, are usually performed using either trial-and-error tuning approaches or back-propagation (BP) algorithms. Since correlations invariably exist among the different input variables of a system, it is inappropriate to simply assign the fuzzy rule partitions on a variable-by-variable basis. A far better approach is to define arbitrarily-shaped fuzzy regions for the voltage vector

As described above, in the knowledge discovery system proposed in this study, the crisp if-then rules extracted using the HRTNN are fuzzified using a specific-to-purpose fuzzy membership function. In theory, the membership function for the j-th hyper-rectangle, 
instance 

where

is the volume of the j-th hyper-rectangle,

and 

4. Confirmation of Knowledge Discovery
4.1. Overview of SEM
The structural equation modeling (SEM) technique was first proposed by Karl Joreskog of Sweden in 1970. SEM is a multivariate analysis technique designed to explore the sequences of causality (both recursive and non-recursive) among the measured and latent variables of a system. Note that measured variables are those variables whose values can be determined directly, while latent variables are those variables which cannot be directly observed and must therefore be estimated from the measured variables. In other words, SEM comprises both a measurement model and a structural model.
1) Measurement model
The measurement model describes the relationships among the measured variables and the latent variables such
Figure 1. Typical arbitrarily-shaped fuzzy rule partitions.
that the latent variables can be constructed (estimated) from the known values of the measured variables. Mathematically, the measurement model can be expressed as

where










2) Structural model
The structural model (also known as the latent variable mode) describes the causality (both unidirectional and bidirectional) among the latent variables. Mathematically, the structural model can be expressed as

where





4.2. Second-Order CFA of SEM to Confirm Knowledge Discovery
In the section above, the coefficient matrix of the measurement model describes the relationships among the measured variables and the latent variables, while the coefficient matrix of the structural model describes the relationships among the latent variables. In this section, the two-stage confirmatory factor analysis (CFA) of the SEM methodology is performed in order to confirm the validity of the causal path constructed in the structural model.
Byrne (2005) showed that the existence of a common latent variable among the higher-level latent variables (second-order latent variables can be detected by performing a second-order CFA [22] . Figure 2 illustrates the two-stage CFA performed in the present study to confirm knowledge discovery.
In the knowledge discovery system proposed in this study, the fuzzy logic rules extracted by the HRTNN are used to evaluate the system state based on the dynamic system data. Therefore, in performing the CFA, the structural model is formulated as follows:

where 




5. Illustrative Example
In this section, the validity of the proposed knowledge discovery system is demonstrated by performing the stability assessment of a real-world nonlinear system, namely the American Electric Power (AEP) 14 bus system
Figure 2. Second-order CFA model for confirming knowledge discovery.
[23] . It is noted that this power system is characterized by non-smooth, non-continuous and non-differentiable functions.
In the proposed approach, the input vector has the form 
to ensure the success of the HRTNN-based knowledge discovery system. In the present study, the HRTNN is trained using both an SDDL algorithm and a BP algorithm. The SDDL algorithm is used to divide the input vector space into proper subsets, i.e., hyper-rectangles, where each hyper-rectangle corresponds to a hidden node,
is n-dimensional, and is defined by 




characteristics of the HRTNN, then HRTNN can to extracted rules of knowledge discovery for stability assessment, represented as hyper rectangles in the input vector space of nonlinear system.
In performing the knowledge discovery process, the input vector was populated using state data acquired from a nonlinear AEP-14 bus system, and 14 PMUs were assigned to the 14 buses in the network. The voltage and phase data of the 14 monitored buses were used to populate the input vector for the HRTNN, and was specified in the form
where 

As described in Section 4.2, the performance of the proposed knowledge discovery system was verified by means of a second-order CFA investigation. The research model was tested using AMOS v.17.0 [24] for confirmatory facto analysis and using the model of equation (18) approach to parameter estimation for extracted rules by exploratory facto analysis. Since the AEP-14 bus system is a nonlinear system, the measured variables do not conform to a normal distribution. Thus, to ensure the convergence of the CFA results, bootstrapping [25] was applied to the sample first, and parameter estimation was performed thereafter. Figure 3 illustrates the CFA results obtained for the present knowledge discovery system.
The CFA parameters of the hypothetical model for the proposed knowledge discovery system are estimated to be smooth. An overall assessment of the model was further performed by using a Fit Index (FI) method [26] to evaluate the fit between the hypothetical model and the actual observed data. The corresponding results are presented in Table 2.
It is observed that for each of the six considered FIs, the value obtained for the current hypothetical model ex-
Figure 3. CFA parameters of hypothetical model for knowledge discovery.
Table 1. Fuzzy rules extracted by HRTNN for AEP-14 bus system.
Table 2. Fit Indexes for hypothetical model.
ceeds the specified fitting standard. In other words, the validity of the proposed knowledge discovery system in successfully diagnosing the state of the AEP-14 bus based on its dynamic data is confirmed.
6. Conclusion
This study has proposed a knowledge discovery system for determining the operational state of a nonlinear system based on an inspection of its dynamic data. In the proposed approach, a synchronized phasor measurement technique is used to acquire the dynamic data of the nonlinear system, and a hyper-rectangle type neural network (HRTNN) is then applied to extract a set of fuzzy rules for determining the system stability. The effectiveness of the proposed approach has been demonstrated using a real-world AEP-14 bus system for illustration purposes. Moreover, the validity of the extracted rules has been confirmed by the means of a two-stage CFA investigation. Finally, the overall performance of the proposed system has been demonstrated by evaluating six Fitness Indexes. The results have shown that the proposed methodology represents a feasible basis for the development of an effective rule-based system for knowledge discovery on real-life dynamic nonlinear systems.
Acknowledgements
This study was supported financially by the National Science Council of Taiwan under Grant No. NSC101-2410- H-252-001.
Cite this paper
Chen-SungChang, (2015) Knowledge Discovery from Dynamic Data on a Nonlinear System. Open Journal of Applied Sciences,05,576-585. doi: 10.4236/ojapps.2015.510056
References
- 1. McClean, S., Scotney, B., Morrow, P. and Greer, K. (2005) Knowledge Discovery by Probabilistic Clustering of Distributed Databases. Data and Knowledge Engineering, 54, 189-210. http://dx.doi.org/10.1016/j.datak.2004.12.001
- 2. Cuzzocrea, A. (2010) Advanced Knowledge-Based Systems. Data and Knowledge Engineering, 69, 661-663. http://dx.doi.org/10.1016/j.datak.2010.02.001
- 3. Nura, E., Mohammad, R.B., Amir-Masoud, E.M. and Vahid, K.T. (2014) Knowledge Discovery in Medicine: Current Issue and Future Trend. Expert Systems with Applications, 41, 4434-4463. http://dx.doi.org/10.1016/j.eswa.2014.01.011
- 4. Lau, R.Y.K., Li, Y., Song, D. and Kwok, R.C.W. (2008) Knowledge Discovery for Adaptive Negotiation Agents in E-Marketplaces. Decision Support Systems, 45, 310-323. http://dx.doi.org/10.1016/j.dss.2007.12.018
- 5. Nkambou, R., Fournier-Viger, P. and Nguifo, E.M. (2011) Learning Task Models in Ill-Defined Domain Using a Hybrid Knowledge Discovery Framework. Knowledge-Based Systems, 24, 176-185. http://dx.doi.org/10.1016/j.knosys.2010.08.002
- 6. Kwong, C.K., Chan, K.Y. and Tsim, Y.C. (2009) A genetic Algorithm Based Knowledge Discovery System for the Design of Fluid Dispensing Processes for Electronic Packaging. Expert Systems with Applications, 36, 3829-3838. http://dx.doi.org/10.1016/j.eswa.2008.02.041
- 7. Guruler, H., Istanbullu, A. and Karahasan, M. (2010) A New Student Performance Analysing System Using Knowledge Discovery in Higher Educational Databases. Computers and Education, 55, 247-254. http://dx.doi.org/10.1016/j.compedu.2010.01.010
- 8. Chen, X. and Wang, D. (2012) Management of Geometric Knowledge in Textbooks. Data and Knowledge Engineering, 73, 43-57. http://dx.doi.org/10.1016/j.datak.2011.10.004
- 9. Phadke, A.G. and Thorp, J.S. (1991) Improved Control and Protection of Power System through Synchronized Phasor Measurements. Control and Dynamic system, 43, 335-376.
- 10. Phadke, A.G. (1993) Synchronized Phasor Measurements in Power Systems. IEEE Computer Applications in Power, 6, 10-15. http://dx.doi.org/10.1109/67.207465
- 11. Moxley, R. (2006) Practical Application of Synchronized Phasor Measurement. 2006 Power Systems Conference: Advanced Metering, Protection, Control, Communication, and Distributed Resources, Clemson, 14-17 March 2006, 73- 82. http://dx.doi.org/10.1109/psamp.2006.285374
- 12. Rasmussen, J. and Jorgensen, P. (2006) Synchronized Phasor Measurements of a Power System Event in Eastern Denmark. IEEE Transactions on Power System, 21, 278-284. http://dx.doi.org/10.1109/TPWRS.2005.860947
- 13. Leick, A. (1994) GPS Satellite Surveying. 2nd Edition, Wiley Inter-Science, Hoboken.
- 14. Simpson, P.K. (1992) Fuzzy Min-Max Neural Networks. Part 1: Classification. IEEE Transactions on Neural Networks, 3, 776-786. http://dx.doi.org/10.1109/72.159066
- 15. Abe, S. and Lan, M.S. (1995) Fuzzy Rules Extraction Directly from Numerical Data for Function Approximation. IEEE Transactions on System, Man and Cybernetics, 25, 119-129. http://dx.doi.org/10.1109/21.362960
- 16. Liu, X.D., Feng, X.H. and Pedrycz, W. (2013) Extraction of Fuzzy Rules from Fuzzy Decision Trees: An Axiomatic Fuzzy Sets (AFS) Approach. Data and Knowledge Engineering, 84, 1-25. http://dx.doi.org/10.1016/j.datak.2012.12.001
- 17. Su, M.C. (1993) A Neural Network Approach to Knowledge Acquisition. PhD Thesis, University of Maryland, College Park.
- 18. Kline, R.B. (1998) Principles and Practice of Structural Equation Modeling. Guilford, New York.
- 19. Kelloway, E.K. (1995) Structural Equation Modeling in Perspective. Journal of Organizational Behavior, 16, 215-224. http://dx.doi.org/10.1002/job.4030160304
- 20. Martínez-Torres, M.R. (2006) A Procedure to Design a Structural and Measurement Model of Intellectual Capital: An Exploratory Study. Information and Management, 43, 617-626. http://dx.doi.org/10.1016/j.im.2006.03.002
- 21. Toral, S.L., Barrero, F. and Martínez-Torres, M.R. (2007) Analysis of Utility and Use of a Web Based Tool for Digital Signal Processing Teaching by Means of a Technological Acceptance Model. Computers and Education, 49, 957-975. http://dx.doi.org/10.1016/j.compedu.2005.12.003
- 22. Byrne, M.B. (2005) Factor Analytic Models: Viewing the Structure of an Assessment Instrument from Three Perspectives. Journal of Personality Assessment, 85, 17-32. http://dx.doi.org/10.1207/s15327752jpa8501_02
- 23. Chang, C.S. (2011) A Matrix-Based VaR Model for Risk Identification in Power Supply Networks. Applied Mathematical Modeling, 35, 4567-4574. http://dx.doi.org/10.1016/j.apm.2011.03.032
- 24. Byrne, M.B. (2001) Structural Equation Modeling with AMOS: Basic Concepts, Applications, and Programming. Lawrence Erlbaum Associates, Mahwah.
- 25. Jonathan, N. and Hancock, G.R. (2001) Performance of Bootstrapping Approaches to Model Test Statistics and Parameter Standard Error Estimation in Structural Equation Model. Structural Equation Modeling, 8, 353-377. http://dx.doi.org/10.1207/S15328007SEM0803_2
- 26. Raines-Eudy, R. (2001) Using Structural Equation Modeling to Test for Differential Reliability and Validity: An Empirical Demonstration. Structural Equation Modeling, 7, 124-141. http://dx.doi.org/10.1207/S15328007SEM0701_07







