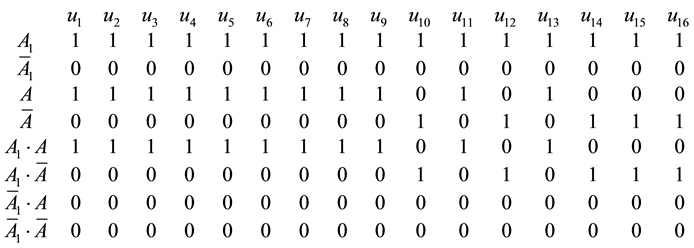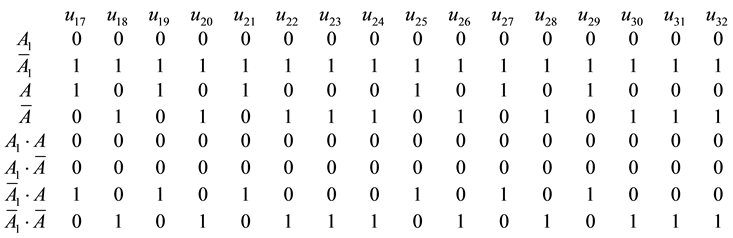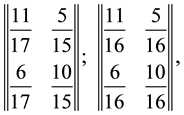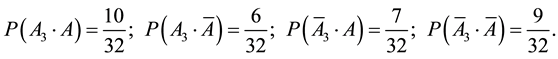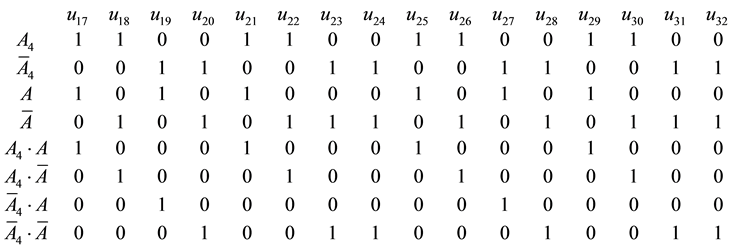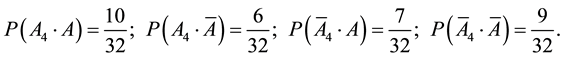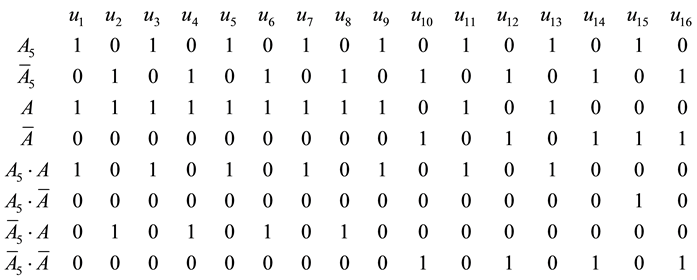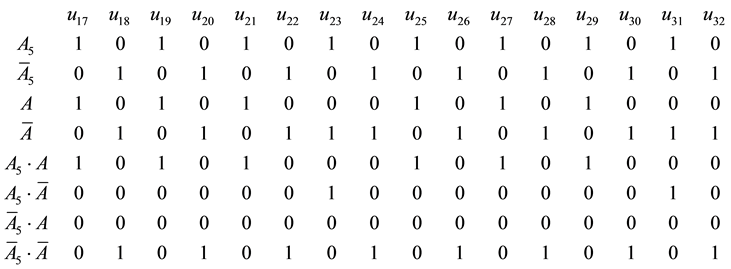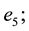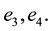Open Journal of Applied Sciences
Vol.05 No.11(2015), Article ID:61036,9 pages
10.4236/ojapps.2015.511066
Matrix Method for Determining Structural Reliability of the System and Significance of Its Elements in Terms of Reliability
Victor Kravets1, Vladimir Kravets2, Olexiy Burov3
1Department of Automobiles and Transportation Facilities Automobile Sector, National Mining University, Dnipropetrovsk, Ukraine
2Department of Labor Security, Dnipropetrovsk National University of Railway Transport Named after Academician V. Lazaryan, Dnipropetrovsk, Ukraine
3Baskin School of Engineering, University of California-Santa Cruz, Santa Cruz, USA

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 14 October 2015; accepted 9 November 2015; published 12 November 2015

ABSTRACT
Matrix method is being proposed for qualitative evaluation of the reliability of technical systems on a finite set of structural elements. We are introducing the criteria for qualitative assessment of the reliability in the form of structural reliability of the system as the probability of the troubleproof state of this system and the significancy of the individual elements in ensuring the structural reliability of the system as a general aggregate of conditional probabilities, which compose two (2 × 2) matrices of significancy for each element. We are using chain diagrams for solving the combinatronic problems and matrices for algorithmization of calculating procedures.
Keywords:
Structural Reliability, Matrices of Significance, Matrix of States, Chain Diagram

1. Introduction
The reliability of the technical system is one of the main indicators of quality and is taken into consideration in the early stages of design, which addresses different functional, assembling and construction schemes [1] . The technical system consists of a set of related and interacting elements, and operates in conditions of both internal and external random factors [2] .
The method of function of the technical system can be implemented with various structures. In general, these structures determine the reliability of the designed technical system. The ability to assess the structural reliability of the individual blocks and the technical system as a whole, as well as to assess the significance of the individual blocks in ensuring the reliability of the system is the relevant problem in conceptual design, which can be solved using mathematical methods, including combinatorial, probability theory, Boolean algebra, matrix calculations [3] .
The matrix method, which will be described further, allows both qualitative and quantitative reliability study including structural reliability as well as the importance of the individual elements in this reliability. The method is adapted to the use modern computer technologies to solve complex combinatorial problems in assessing the reliability of technical systems on an arbitrary, finite set of structural elements [4] [5] .
2. Content
2.1. Formulation of the Problem
It is assumed that the structure of a technical system is given as a finite set of elements and their relationships. It is required to find the value of structural reliability and evaluate the importance of each element in ensuring the reliability of the overall system.
2.2. Structural Reliability
Structural reliability is calculated using the classical formula of calculating the probability
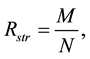 (1)
(1)
where N is the number of possible states of the system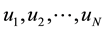 ; M is the number of working states of the system.
; M is the number of working states of the system.
The number of possible states of the system is calculated using the following formula:
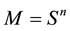 (2)
(2)
where n is the number of elements in the system; S is the number of states of each element.
We assume that each element of the system can be in one of two states: operating (working) or failure, i.e.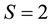 . Then
. Then
 (3)
(3)
In the case where the elements of the system have the ability to be in one of three states: working, neutral and failure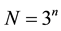 , etc.
, etc.
2.3. State Diagram
The determination of a finite set of possible states of the system
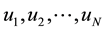 is a combinatorial problem, which is conveniently resolved through chain diagram. Creating the diagram of the states of the system allows us not only to establish the total number of different possible states of the system N, but also to get the specific value of each state of the system
is a combinatorial problem, which is conveniently resolved through chain diagram. Creating the diagram of the states of the system allows us not only to establish the total number of different possible states of the system N, but also to get the specific value of each state of the system
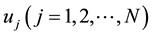 depending on the status of each individual element
depending on the status of each individual element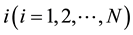 .
.
2.4. State Matrix
The state diagram of the system can be represented by a rectangular matrix of states, which has the dimension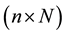 , i.e., rows of the matrix are determined by the number of the elements in the system and columns―the number of possible states-N. The status of each element is a random event
, i.e., rows of the matrix are determined by the number of the elements in the system and columns―the number of possible states-N. The status of each element is a random event
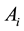 that has two possible values: 1―operating (working) state, 0―failure (not working) state, the probability of which is determined by the reliability and unreliability of the respective element, i.e., State Matrix is a rectangular matrix of size
that has two possible values: 1―operating (working) state, 0―failure (not working) state, the probability of which is determined by the reliability and unreliability of the respective element, i.e., State Matrix is a rectangular matrix of size
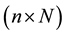 and is composed of ones and zeroes in accordance with State diagram.
and is composed of ones and zeroes in accordance with State diagram.
2.5. State of the System
State of the system in general is also a random event A, which has two possible values that are determined using the matrix of state depending on the structural scheme being considered and is presented by a row matrix .
.
The states of the system are determined by a random state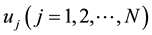 , composing the whole group of exclusive random equally possible events, i.e. cases. Then the number of working states M of the system A can be determined as a sum of corresponding and independent random events
, composing the whole group of exclusive random equally possible events, i.e. cases. Then the number of working states M of the system A can be determined as a sum of corresponding and independent random events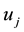 , i.e. the problem of determining the structural reliability of the system in general is solved in accordance with classical formula of probability
, i.e. the problem of determining the structural reliability of the system in general is solved in accordance with classical formula of probability
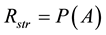
2.6. Significance of the Element in the System Depending on Reliability
In general the assessment of different separate elements in ensuring the structural reliability of the system is done using matrices of significance that have the following form


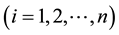
The conditional probabilities that compose these matrices can be calculated using formulas:



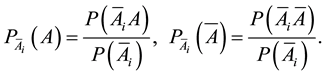
These conditional probabilities characterize to which extent operation or failure of a single element is reflected on working or failure state of the whole system, i.e. on structural reliability or unreliability of the system, as well as how important this element is to ensure working state of the system as a whole. Note that considered here conditional probabilities satisfy the following conditions:


which can be used for verification immediately by definition we get:

and also
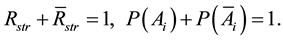
We are considering products (intersections) of random events of the following types:

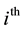
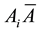


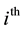
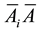

For each

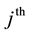
From the created matrices
Basic theoretical principles of the described method are shown in [3] . The method was applied for determining structural reliability of the electrical block of the hybrid car and for assessment of significance of separate elements in ensuring the reliability of the system as a whole [4] . The described matrix method is represented as an algorithm, which can be used for calculating the reliability of the described qualitative characteristics of the specific system composed of five elements (penta-system).
3. Algorithm
The algorithm will be illustrated as an example on one of the finite set of structural schemes of the penta-system. Elements of the system can be connected by either series or parallel principle. Chosen structural scheme is filled with five inhomogeneous, independently working elements as shown in Figure 1.
3.1. Part 1
Determining the number of possible states of the penta-system: 25, i.e.
?working, specified as
?failed, specified as
3.2. Part 2
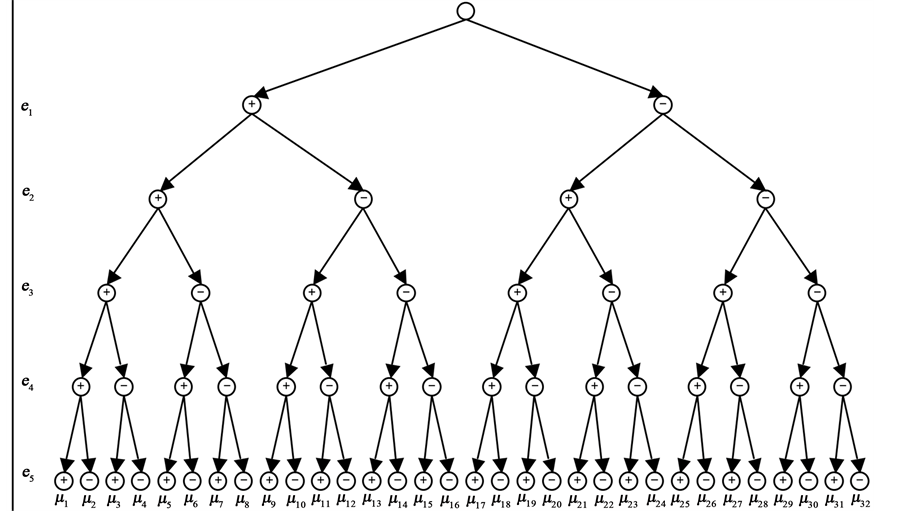
Chain Diagram of states of the penta-system is built (Figure 2).
Using chain diagram (states graph) each of the 32 possible states of the penta-system is found
3.3. Part 3
Rectangular state matrix



Figure 1. Structural scheme of the penta-system.
Figure 2. State diagram of the penta-system.
3.4. Part 4
Then the row-matrix

Here 1 corresponds to the working state of the penta-system, while 0 to failed state respectively.
3.5. Part 5
Structural reliability of the specified penta-system is determined:
Here the working state of the penta-system as a whole and the corresponding possible state are considered as random events, i.e.
3.6. Part 6
Matrixes of significance of each element of the penta-system
i.e.
Then, obviously, probability of a random event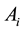

1) The calculation matrix for the second element
From which one can get probabilities of multiplication of needed random events, i.e.:
Then matrixes of significances for the first element will take the following form:
2) The calculation matrix for the second element

Then:
Consequently:
i.e. elements 1 and 2 have the same significance in ensuring the reliability of the considered penta-system.
3) The calculation matrix for the second element

Then:
Consequently:
i.e. significance of the third element is lower than the significances of elements 1 and 2.
4) The calculation matrix for the second element (i = 4) is constructed. The calculation matrix then has the following form:
Then:
Consequently:
i.e. elements 3 and 4 have the same significance in ensuring the reliability of the considered penta-system.
5) The calculation matrix for the second element

Then:
Consequently:
i.e. the significance of the fifth element in ensuring the reliability of the penta-system is the highest.
3.7. Part 7
The elements of the system

1)
2)
3)
4. Conclusion
Research on the reliability of technical systems on a finite set of structural elements is proposed to carry out on the basis of the developed matrix method that also allows to effectively applying modern computer technologies for solving multidimensional combinatorial problems. Algorithms for the qualitative assessment of the reliability of technical systems, structural reliability, the significance of the reliability of individual elements using chain diagrams of states, State Matrices, Matrices of Significance were developed.
Cite this paper
VictorKravets,VladimirKravets,OlexiyBurov, (2015) Matrix Method for Determining Structural Reliability of the System and Significance of Its Elements in Terms of Reliability. Open Journal of Applied Sciences,05,669-677. doi: 10.4236/ojapps.2015.511066
References
- 1. Hubka, V. and Eder, W.E. (1988) Theory of Technical Systems: A Total Concept Theory for Engineering Design. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-3-642-52121-8 - 2. Вентцель, Е.С. and Овчаров, Л.А. (1991) Теория случайных процессов и ее инженерные приложения. Наука, Москва.
- 3. Kravets, V.V. and Kravets, Vl.V. (2015) Reliability of the Systems. Part 1. Statics of the Failure. Lap Lambert Academic Publishing, Omni Scriptum GmbH & Co. KG.
- 4. Kravets, V.V., Bass, K.M. and Kravets, Vl.V. (2013) Structural Reliability of the Electrical Unit Hybrid Vehicle. System Technologies, 2, 161-166.
- 5.Kravets, V.V., Bass, K.M., Kravets, Vl.V. and Tokar, L.A. (2014) Analytical Solution of Kolmogorov Equations for Four-Condition Homogenous Symmetric and Ergodic System. Open Journal of Applied Sciences, 4, 497-500.
http://dx.doi.org/10.4236/ojapps.2014.410048