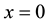Open Journal of Applied Sciences
Vol.05 No.09(2015), Article ID:59818,9 pages
10.4236/ojapps.2015.59052
Age-Structured Population Projection of Bangladesh by Using a Partial Differential Model with Quadratic Polynomial Curve Fitting
Shirin Sultana1, Mahmudul Hasan2, Laek Sazzad Andallah2
1Department of Natural Sciences, Daffodil International University, Dhaka, Bangladesh
2Department of Mathematics, Jahangirnagar University, Dhaka, Bangladesh
Email: shirn.ns@daffodilvarsity.edu.bd, smmhasan@juniv.edu, andallah@juniv.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 June 2015; accepted 20 September 2015; published 23 September 2015
ABSTRACT
In this paper, the age-specific population of Bangladesh based on a linear first order (hyperbolic) partial differential equation which is known as Von-Foerster Equation is studied. Applying quadratic polynomial curve fitting, the total population and population density of Bangladesh are projected for the years 2001 to 2050 based on the explicit upwind finite difference scheme for the age-structured population model based on given data (source: BBS & ICDDR, B) for initial value in the year 2001. For each age-group, the future birth rates and death rates are estimated by using quadratic polynomial curve fitting of the data for the years 2001 to 2012. Quadratic polynomial curve fitting is also used for the boundary value as the (0 - 4) age-group population based on the population size of the age-group for the years 2001 to 2012.
Keywords:
Von-Foerster Equation, Birth Rate, Death Rate, Curve Fitting

1. Introduction
The fast growth of population during the past decades has frustrated the development efforts in Bangladesh. In 1971 the population of the country was around 75 million. According to the 5th census of Bangladesh Bureau of Statistics (BBS) in 2011, the total population of Bangladesh is 150 million. The area of Bangladesh is 147,570 square kilometers only and it is one of the most densely populated countries all over the world. To handle such mass population in such short land is a huge problem for the government to take any developing steps. Due to scarcity of resources, it is not possible to provide educational, health, medical, transport and housing facilities to the entire population. A rapidly increasing population plugs the economy into mass unemployment and under employment. As a result, the actual development is just getting being delayed a hampered a lot. With the help of population model, we can predict what the number of population will be by the year of 2050. Therefore, the government should take immediate steps to keep the population under control and the people themselves should adopt family planning for their own benefit. In order to make an efficient planning for the demands of different age-group, it is important to predict the age-structured population of the country. Therefore, in this paper we project the future age-structured population of Bangladesh based on a partial differential equation model. The information we get from age-specified population group can help us in future planning of social and economical development. For example, if we can predict the population of children of 0 - 4 years old, we can provide necessary medical care and baby food to reduce the mortality rate and keep children healthy and nourished. After 50 years of liberation of Bangladesh, the government of Bangladesh is going to celebrate the year 2021 as “apotheosis of liberation”. The government has already declared the year as “vision 2021”. To educate the people of Bangladesh within 2021, we can afford necessary support for children of 4 - 15 years old. We can provide human resource development program for young people to reduce the unemployment problem and also proper health care to elder people.
2. Age-Structured Population Model
For the prediction of age-structured population, various differential equation models have been formulated by different Mathematicians in different time. In [1] , Murray studies the linear age structure population model where he used time-independent death rate. An extensive study of linear and nonlinear age-dependent population dynamics can be found in the works of Webb [2] , Gurtin [3] and Iannelli [4] .
In this paper, we study a linear first order hyperbolic partial differential equation to predict age?dependent population. We project the future age-structured population in Bangladesh based on this linear model of population which is known as Von-Foerster equation, given as follows:
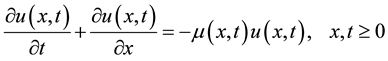 (1)
(1)
with 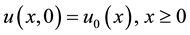
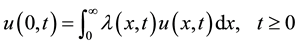
where, 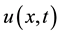 is the age density function,
is the age density function, 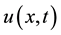 the age specific death rate,
the age specific death rate, 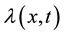 the age specific fertility rate so that
the age specific fertility rate so that 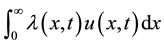 is the birth rate and
is the birth rate and 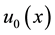 is the initial age distribution.
is the initial age distribution.
3. Numerical Scheme for the Model
The age-structured population model can be written as
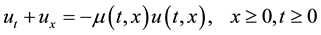 (2)
(2)
with initial condition
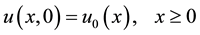 (3)
(3)
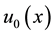 a nonnegative function, and a boundary condition at
a nonnegative function, and a boundary condition at 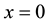 (the inflow boundary of the domain)
(the inflow boundary of the domain)
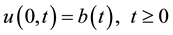 (4)
(4)
Based on [5] and [6] we discretize the time derivative by a forward difference formula, and the age derivative with a backward difference on a discrete mesh 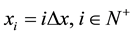 and
and . The forward difference
. The forward difference
approximation for 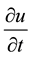 obtained by the Taylor series formula is
obtained by the Taylor series formula is
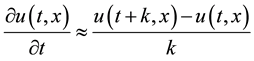
and the backward difference approximation for 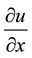
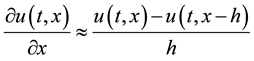
We consider uniform grid spacing with step size h and k for space and time respectively, 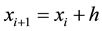
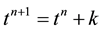
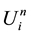
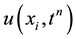
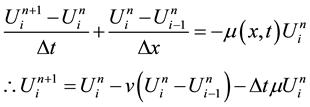
which is the explicit upwind difference scheme for the age-structured population model.
Here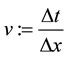
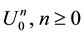
and initial value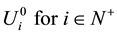
4. Numerical Experiments
We implement the explicit upwind difference scheme and introduce quadratic polynomial curve fitting procedure for the age-structured population model.
4.1. Curve Fitting
Curve fitting is the process of constructing a curve, or mathematical function that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a “smooth” function is constructed that approximately fits the data.
4.2. Quadratic Polynomial Models
Given n data points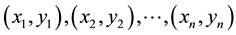
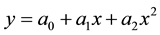
The residual at each data point is given by
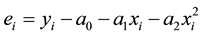
The sum of the square of the residuals is given by
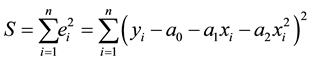
To find the constants of the polynomial regression model, we put the derivatives successively with respect to 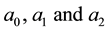
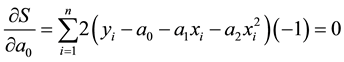
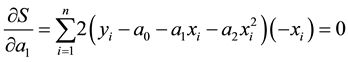
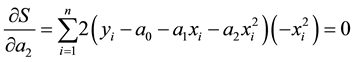
Setting those equations in matrix form gives
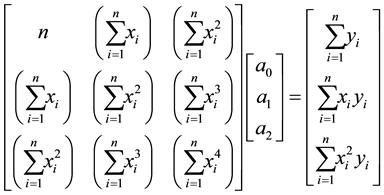
The above are solved for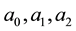
4.3. Incorporation of Data into Explicit Upwind Difference Scheme
To predict the Age Distributed Population we incorporate the initial and boundary data into the Explicit Upwind Scheme with respect to the assumptions and considerations below:
We assume that 
・ We have considered the age of people of Bangladesh in between 0 to 85+ years. We divide this age-group (0 to 85 years) into 18 sub-groups, each sub-group contains 5 years interval i.e. 0 - 4, 5 - 9, 10 - 14, ・・・, 80 - 84, 85+.
・ We have used age distributed population of 2001 as initial data 
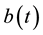
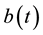
Table 1. Mid-year population distribution in percentage by age-group from 2001 to 2012.
(Source: ICDDR, B).
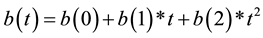
Then we have used 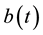
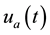
・ We have estimated death rate, which has been parameterized by 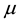
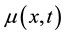
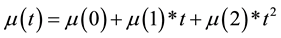
For this we have used data of death rate from Table 2 [8] .
Using theses age and time dependent death rate, initial value and boundary condition on Explicit Upwind Finite Difference Scheme, we can forecast the age specific population distribution.
4.4. Total Population Projection
Figure 1 shows our estimated total population projection marked by “Age-Structured Population Model (By Quadratic Polynomial)” for the years 2001 to 2050. Here it is observed that the initial population in our model is 131 million for the year 2001 and the predicted population for the year 2050 is 246.3280 million. In the year 2021, in our model the predicted population will be 170.2044 million whereas the total population was 75 million in 1971. So the total population in 2021 will be 2.26 multiple of the total population of 1971.
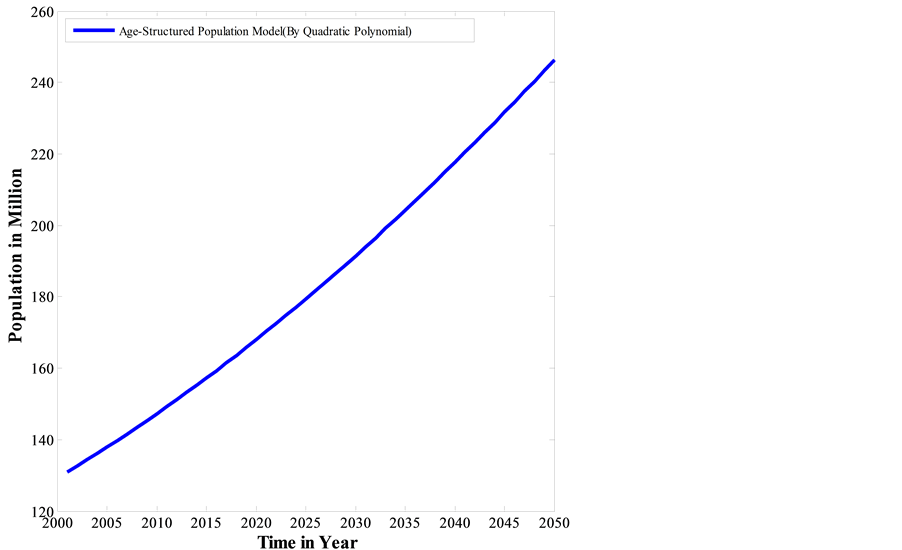
Figure 2 shows the comparison of the predicted population of Bangladesh from the years 2001 to 2050 with the projection of Bangladesh Bureau of Statistics (BBS) which is made by Md. Kabir [9] , the predicted population by Dutta and Andallah [10] and the predicted population by Md. Minarul Haque, Faruque Ahmed, Sayedul Anam, Md. Rashed Kabir [11] . Here, the population of Bangladesh is calculated by three mathematical methods. Dutta and Andallah have used “Linear Equation”, Md. Minarul Haque, Faruque Ahmed, Sayedul Anam, Md.
Table 2. Death rate by age-group and year (per 1000 population).
(Source: ICDDR, B).
Figure 1. Example of a figure caption (figure caption).
Figure 2. Comparison of our population projection with different methods.
Rashed Kabirhave used “Logistic Population Model” and we have used “Quadratic Polynomial Curve Fitting”. Our curve is going to most nearer to the curve of Logistic Population Model with the increased period of time. Here it is observed that the initial population is 131 million in 2001 in our projection as well as same in the projection by Linear Equation where as it is 130.02 in the projection of BBS and 129.090 million in the projection by Logistic Population Model. It is also observed that, for the year 2050 our predicted population is 246.3280 million, but it is 294.38 million corresponding to BBS and 283.8058 corresponding to the projection by Linear Equation.
In 2035, in our model the predicted population will be 204.2385 million whereas the predicted population will be 235.67 million corresponding to the projection of BBS, 232.5276 million corresponding to the projection by Linear Equation and 205.979 million corresponding to the projection by Logistic Population Model. By Figure 2 one can observe that the inclination of the increasing population of our Age-Structured Population Model is more consistent than the demographical method of BBS and the population model by Linear Equation. From the comparison it is also observed that the prediction by the Quadratic Polynomial Curve Fitting method is much closer to the prediction by Logistic Population Model.
4.5. Population Projection for Different Age-Groups
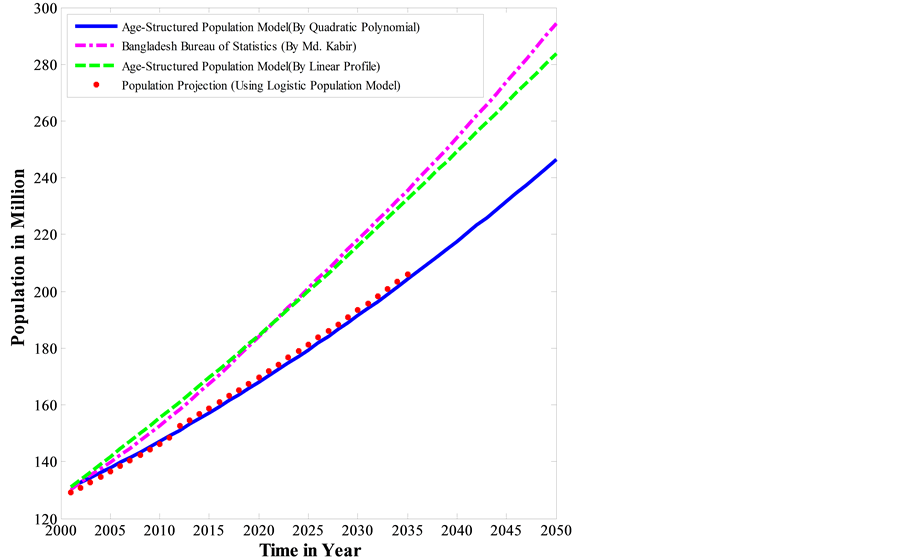
Figure 3 is showing the population projection for different age-groups of Bangladesh from the years 2001 to 2050. It is clearly observed that, the age of the people in the scale (0 - 15) will increase rapidly. The middle aged people will also increase but the increasing rate will be partially sloth and the increasing rate of aged people will be very sloth.
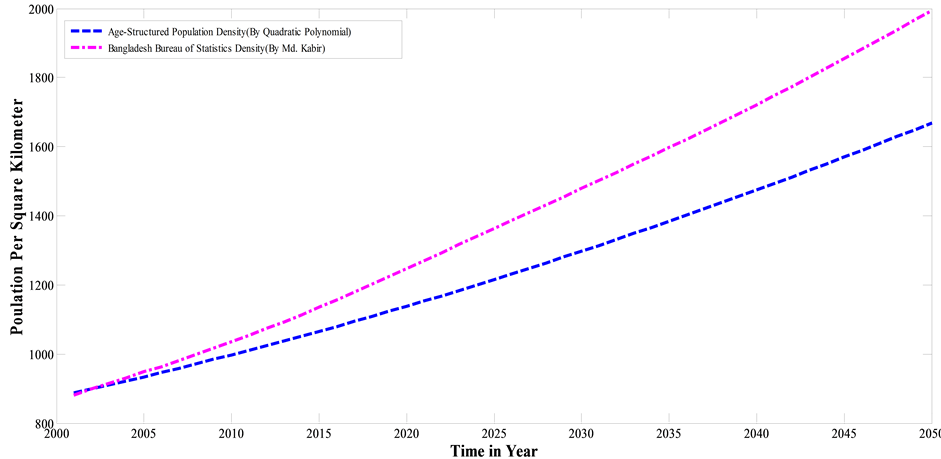
Figure 4 shows the comparison of our estimated population per-square kilometer projection marked by “Age- Structured Population Density (By Quadratic Polynomial)” with that of marked by “Bangladesh Bureau of Statistics Density (by Md. Kabir)” for the years 2001 to 2050. Here it is observed that the initial population per- square kilometer is 888 in 2001 in our projection whereas it is 881 according to the projection of BBS. It is also observed that, for the year 2050 our predicted population per-square kilometer is 1669, but it is 1995 according to BBS. In 2021, in our model the predicted population per-square kilometer will be 1153 whereas the predicted population per-square kilometer will be 1271 according to the projection of BBS.
The total predicted population for the years 2001 to 2050 is presented in Table 3 and the predicted population per-square kilometer is presented in Table 4.
5. Conclusion
We have considered a continuous and deterministic mathematical model known as Von-Foerster model, which is a linear first order partial differential equation used to predict population distribution by age at any time, given the initial distribution and the variation of birth and death rates with age and time. Although this is a linear equation, it is not easy to solve the difficulty of enforcing boundary condition. For this, we have used finite difference
Figure 3. Population projection of different age-groups.
Table 3. Population projection of Bangladesh from 2001 to 2050 (in millions).
Table 4. Population per-square kilometer of Bangladesh from 2001 to 2050.
Figure 4. Comparison of our population density projection with Bangladesh Bureau of Statistics for the years 2001 to 2050.
method for the numerical solution of the age-structured population model. For the numerical experiment, the year 2001 is used as the initial time. We have predicted the age distribution population up to the year 2050. In this experiment we have provided the data for birth rate and death rate up to 2012 from [7] and [8] respectively. The results have showed a “very good agreement” with the age distribution population size up to 2012 given in [7] . These have justified the correctness of our implementation of the explicit upwind finite difference scheme for the age-structured population projection in Bangladesh and in other countries as well. We have predicted the total population and population density up to 2050 and these results have showed a very good agreement with the results according to the projection by Logistic Population Model [11] which have been predicted up to 2035. We have observed that, in the year 2050, our population will be 246.3280 million whereas it is 294.38 million according to Kabir [9] and 283.8058 million according to the projection by Linear Equation [10] . In [10] , the calculation is based on a linear modeling of birth and death rate and our calculation is based on a quadratic polynomial curve fitting of birth and death rate. We have estimated the birth rate and death rate by a non-linear profile. So, the results are more realistic. This motivates us for further study of the model.
Cite this paper
ShirinSultana,MahmudulHasan,Laek SazzadAndallah, (2015) Age-Structured Population Projection of Bangladesh by Using a Partial Differential Model with Quadratic Polynomial Curve Fitting. Open Journal of Applied Sciences,05,542-551. doi: 10.4236/ojapps.2015.59052
References
- 1. Murray, J.D. (1989) Mathematical Biology. Springer-Verlag, Berlin Hiedelberg.
- 2. Webb, G.F. (1985) Theory of Nonlinear Age-Dependent Population Dynamics. Marcel Dekker Inc., New York.
- 3. Gurtin, M.E. and MacCamy, R.C. (1984) Nonlinear Age-Dependent Population Dynamics. Archive for Rational Mechanics and Analysis, 54, 281-300.
- 4. Iannelli, M. (1995) Mathematical Theory of Age-Structured Population Dynamics. Applied Mathematics Monographs, 7, Consiglio Nazionaledelle Ricerche, Pisa.
- 5. Burden, R.I. and Fairs, J.D. (1997) Numerical Analysis. 6th Edition, Brookscole.
- 6. Abia, L.M., Angulo, O. and Lopez-Marcos, J.C. (2005) Age-Structured Population Models and Their Numerical Solution. Ecological Modelling, 188, 112-136. http://dx.doi.org/10.1016/j.ecolmodel.2005.05.007
- 7. ICDDR, B Document, Table 2.3 Mid-Year Population Distribution by Age Group.
- 8. ICDDR, B Document, Table 3.3 Death Rate by Age and Year (per 1000 Population).
- 9. Kabir, Md. and Ahmed, T. (2006) Poverty-Aging Population Projection. BBS, Ministry of planning, Bangladesh.
- 10. Dutta and Andallah, L.S. (2008) Age-Structured Population Projection in Bangladesh Based on Numerical Solution of a Deterministic Model. Bangladesh Journal of Scientific Research, 21, 65-78.
- 11. Haque, Md.M., Ahmed, F., Anam, S. and Kabir, Md.R. (2012) Future Population Projection of Bangladesh by Growth Rate Modeling Using Logistic Population Model. Annals of Pure and Applied Mathematics, 1, 192-202.