Received 23 April 2015; accepted 10 May 2015; published 12 May 2015

ABSTRACT

In this paper, we present a stock model with Markov switching in the uncertainty markets, where the parameters of drift and volatility change according to the states of a Markov process. To price the option, we firstly establish a risk-neutral probability based on the uncertain measure given by Liu. Then a closed form of the European option pricing formula is obtained by applying the Laplace transforms and the inverse Laplace transforms.

Keywords:

Uncertainty Theory, Markov Process, Laplace Transform, Put-Call Parity, Option Pricing

1. Introduction

The problem of option pricing is one of the most foundational problems in financial world. In 1900, Brownian motion was first introduced to finance by Bachelier [1] . Samuelson [2] proposed that stock prices follow geometric Brownian motion. Following that, Black and Scholes [3] created the famous Black-Scholes model and gave an option pricing formula. Nowadays, it has become an indispensable tool in financial market. In previous option pricing theory, the problems of option pricing were handled under stochastic theory.

In order to study uncertain phenomena in human systems, Liu [4] found an uncertainty theory and refined it based on normality, monotonicity, self-duality and countable subadditivity. In 2008, Liu [5] proposed a concept of uncertain process and defined uncertain differential equation. In 2009, Liu [6] designed a canonical process and invented uncertain calculus. By means of uncertain differential equation, Liu [6] proposed a stock model for uncertain markets that are essentially a kind of markets consistent with uncertain measure. Following that, Chen [7] derived an American option pricing formula.

In reality, some important information may greatly impact the volatility of stock returns, such as a change from “bull market” to “bear market”. Hamilton [8] first studied the regime change and business cycles by using the Markov switching model. Di Masi, Kabanov and Runggaldier [9] considered the problem of hedging a European call option for a diffusion model, where drift and volatility are functions of a two-state Markov process. Guo [10] provided a closed-form formula for the arbitrage-free price of the European call option by using Markov switching model. Cheng et al. [11] carried out further research on Guo’s result. Mamon and Rodrigo [12] got an explicit solution to European options in a Regime-switching economy.

Inspired by the empirical phenomena of stock fluctuations related to the business cycle and the evidence from literatures that validated Markov switching model in the investigation of option pricing, in this paper, we deal with the pricing of options with Markov switching model in uncertainty markets. Specifically, we assume that stock prices are generated by a geometric uncertain process, and that the drift and volatility parameters take different values depending on the state of a Markov process. We finally provide an explicit formula for pricing when the Markov process has two states.

2. Preliminaries

Uncertainty theory is a branch of axiomatic mathematics. It is an evolving system founded by Liu to deal with human uncertainty. Now the book Uncertainty theory has been updated to edition five [13] .

Definition 1. An uncertain process is said to be a canonical Liu process if

a) 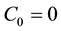and almost all sample paths are Lipschitz continuous,

b) 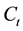has stationary and independent increments,

c) every increment 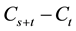is a normal uncertain variable with expected value 0 and variance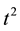, whose uncertainty distribution is

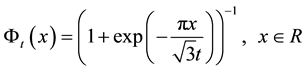(2.1)

If is a canonical process, then the uncertain process is called a geometric canonical process, where 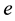is called the log-drift and 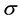is called the log-diffusion.

Definition 2. Let 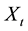be an uncertain process and let 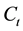be a canonical process. For any partition of closed interval 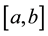with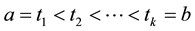, the mesh is written as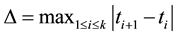. Then the uncertain integral of 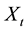with respect to is

(2.2)

provided that the limit exists almost surely and is an uncertain variable.

Definition 3. Suppose is a canonical process, and and are two given functions. Then

(2.3)

is called an uncertain differential equation.

Definition 4. Let be the bond price, and the stock price. Assume that the stock price follows a geometric canonical process. Then Liu’s stock model is

(2.4)

where is the riskless interest rate, is the log-drift, is the log-diffusion, and is a canonical Liu process.

Note that the stock price is

(2.5)

whose uncertainty distribution is

(2.6)

Definition 5. Assume a European call option has a strike price K and an expiration time s. Then the European call option price is

(2.7)

Definition 6. Assume a European put option has a strike price K and an expiration time s. Then the European put option price is

(2.8)

3. Uncertain Stock Model with Markov Switching

Consider the following uncertain stock model which incorporates different states of stock market quotation

(3.1)

where is a stochastic process representing the state of market and is independent of the canonical process. For each state of, the drift parameter, diffusion parameter and riskless interest rate take different values when is in different state.

Assume that is a Markov process with a finite number of states. In this paper, we will focus our discussion on the case of two-state Markov switching model. Specifically, let at those times which the

price change is not abnormal, in this state,. Similarly, let when some significant information just appears and cause turbulence in stock market, then,.

Suppose, further, that each piece of information flow is a random process, and are independent identically distributed processes. Then their super imposed process is Poisson. Consider the transition among different states, let be the rate of leaving state and let be the time interval remaining in state. Then the cumulative distribution function of is as follow:

(3.2)

Then the volatility of stock price is driven by the canonical process and the Markov process.

4. Risk-Neutral Option Pricing Based on the Uncertain Stock Model with Markov Switching

We aim to value the European call option based on the risk-neutral pricing theory, but it is easy to verify that the model is not accord with no-arbitrage hypothesis.

As we know, in a risk-neutral framework, the Option Put-Call Parity Relation is as follow:

(4.1)

where C is the European call option price, P is the European put option price, K is the same strike price and is the initial stock price.

But from the Definition 5 and Definition 6, we can learn:

(4.2)

(4.3)

Then

(4.4)

in which, and are indicator functions.

And according to Kai Yao (2010) [14] ,

(4.5)

so,

(4.6)

Therefore, no option put-call parity Relation was created between and. They were not priced in the risk-neutral measure. So we need to find the risk-neutral measure.

Lemma 1. Consider the uncertain stock model (2.4), when, the risk-neutral uncertainty distribution of is as follow:

(4.7)

Proof: As we know, in the risk-neutral measure, the expected stock return is equal to the riskless interest rate. Assume that is the risk-neutral uncertainty distribution of, is the risk-neutral expected value of.

Following from (4.5), we have:

(4.8)

In the risk-neutral measure, the expected value of is:

(4.9)

Let, then

(4.10)

(4.11)

If:

(4.12)

Then:

(4.13)

(4.14)

Then we have:

(4.15)

So when:

(4.16)

Thus, the risk-neutral uncertainty distribution function is verified.

Then we will present the following theorem for a two-state Markov switching model. Let be occupation time of state 0, when the chain starts from state. That is the total amount of time between 0 and T during

which, starting from state for i = 0, 1. Let be the uncertainty distribution function of.

Theorem 1. Under the Markov switching uncertain stock model (3.1) and the risk-neutral uncertainty distribution (4.7), the arbitrage free price of European call option with expiration date T and strike price K is given by

(4.17)

where is the derivative of the risk-neutral uncertainty distribution.

(4.18)

(4.19)

(4.20)

where and are the modified Bessel functions, defined as (a = 0, 1)

(4.21)

is the uncertainty distribution function of and is the unit impulse function.

Proof: Since the arbitrage price of the European option is the discounted expected value of under the risk-neutral uncertainty measure, we have:

(4.22)

Consider and it’s uncertainty distribution function, then according to the smoothing property of conditional expectation, we have

(4.23)

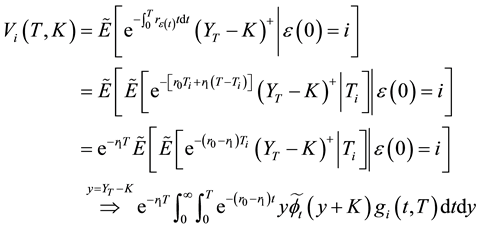
where is the derivative of the risk-neutral uncertainty distribution.

Next we will deduce the form of using Laplace transform and inverse Laplace transform. Note that is the uncertainty distribution function of and, where is the indicator function of state 0.

Let

(4.24)

is the Laplace transform of with respect to t.

Assume that the time interval of state changing obeys the exponential distribution, as shown in (3.2), then by considering the total probability of and, , we have

(4.25)

(4.26)

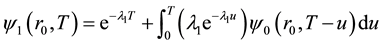
Then taking Laplace transforms with respect to T on both sides. By using the convolve formula, we get:

(4.27)

Specifically,

(4.28)

(4.29)

We obtain:

(4.30)

(4.31)

Then taking the inverse Laplace transforms on both and with respect to.

(4.32)

(4.33)

where is the unit impulse function,.

By using the delay and translation property of Laplace transform, and considering the following facts about the Laplace transform of Bessel functions:

(4.34)

(4.35)

(4.36)

We can take the inverse Laplace transforms on and with respect to.

(4.37)

where is the unit step function

(4.38)

and is the unit impulse function:

(4.39)

So, when, we have:

(4.40)

Similarly,

(4.41)

Substitute for and the Theorem is proved.

5. Conclusion

In this paper, a stock model with Markov switching in the uncertainty markets is proposed to capture the fluctuations related to the business cycle. Then the risk-neutral probability based on the uncertain measure is established for European call option pricing. Finally, an analytical formula of the option price is given by virtue of risk-neutral pricing theory. The model presented in this paper is applicable not only to two states Markov switching but also to general model with finite states Markov process.

References