Received 28 January 2016; accepted 4 April 2016; published 7 April 2016

ABSTRACT

Simulation code for a model of the adaptive immune response seen in flavivirus infections is used to explain the immunopathological consequences seen in West Nile Virus virus (WNV) infections. We use a model that specifically handles the differences in how the virus infects resting cells, the G₀ state, versus dividing cells, the G₁ state, which includes vastly increased MHC-I upregulation for resting cells over dividing cells. The simulation suggests how the infection progresses in a one host model and the results shed insight into the unusual survival curve data obtained for this infection: there is an increase in health even though viral load has increased.

Keywords:

Auto Immune Responses, West Nile Virus, Host Survival Models, MHC-I Upregulation, IFN-g Upregulation, Free Antigen Levels

1. Introduction

The code for the general simulation framework has been discussed in [1] with results in [2] , and the reader is referred to those works for the background details. Further, in that work, we outline how a flavivirus such as West Nile Virus infects its host, and so we will only go over some of that information here.

The family Flaviviridae are single-stranded, plus sense RNA viruses transmitted by arthropods such as mosquitoes and ticks. Flaviviruses induce an increase in expression of major histocompatibility complex, MHC-I and II, as well as other immune recognition molecules, including intracellular adhesion molecule-1 (ICAM-1, CD54), vascular adhesion molecule-1 (VCAM-1, CD106) and E-selectin (CD62E) variously and on a wide variety of cells [3] . WNV-induced increases in cell surface expression of these molecules therefore result in increased efficiency of recognition and killing of infected cells by WNV-specific cytotoxic T lymphocytes, CTL [4] [5] . Increases in MHC-I concentration on infected cells enhance the avidity of interaction of virus-specific CTL with the infected target cell. The increased avidity enables the interaction of infected cells with CTL clones previously below the recognition threshold because of their low affinity for MHC-virus peptide ligand. Furthermore, a polyclonal anti-viral CTL population can include self-reactive low-affinity clones that recognize MHC-I-self peptide configurations as discussed in [5] - [7] . The previous simulation results in [2] offered support for this point of view. Due to the increased avidity of their interaction, these low-affinity, self-reactive clones can now lyse both infected and uninfected target cells that express high cell surface MHC-I concentrations [8] .

Because the avidity of interaction between T cells and their targets can be increased via MHC associated upregulation, any increases in MHC and/or ICAM-1 expression further enhance CTL recognition of target cells. This in turn increases the chances of low-affinity, self-reactive CTL recognizing these target cells. It is also known that the position of the cell cycle is important in flavivirus infection. Non-dividing cells when infected with WNV increase their MHC-I expression 6-10-fold, while infected cycling cells increase MHC-I expression by only 2-3-fold [9] . This results in some 10-fold more lysis of infected target cells than cycling cells by the same CTL [4] . Thus, there is enhanced avidity of interaction between CTL and WNV-infected cells in the nondividing state while infected cycling cells are less easily recognized. Further, WNV replicates significantly better in dividing cells than in non-dividing cells. Thus, virus may be eradicated with relatively poor efficiency in a population of infected cycling cells. In vivo, since most cells are not dividing, the decoy hypothesis asserts it is the small population of infected dividing cells that supports virus replication while maintaining a low immunological profile, thus increasing the probability of virus transmission [5] . High MHC-I expressing (uninfected) targets are therefore susceptible to lysis by low affinity self-reactive CTL clones. A review summarizing the case for an autoimmune component to the West Nile virus infections is in [10] .

In most virus infections, the probability of death of the host varies predictably with viral dose in a dose response curve. Thus, a lower dose results in viral clearance by an efficient immune response that runs its complete course in an infection with no mortality. In contrast, the highest doses produce 100% mortality, which interrupts the immune response before it has managed to clear the virus. In flavivirus infection, however, the mortality associated with intervening doses is unpredictable over several log10 dilutions of virus dose. This results in a ragged dose-response curve depicting population mortality [7] whose data we show in Figure 1. The work in this paper builds on the model of the host-pathogen interactions for flaviviruses detailed in [2] and is used to

explain the ragged dose survival curves seen in these infections.

2. Simple Survival Model Calculations

We can do a simplified calculation to help us see that the presence of MHC-I upregulation should lead to local oscillations in the survival rate. We will do another proof of concept calculation in Section 3 once we have built a model of collateral damage which also suggests that there is a potential for auto immune interaction with the WNV infections. Let 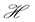denote the population of uninfected dividing and non-dividing cells and, the population of infected non-dividing cells (this is the population of interest). The size of these populations is dependent on the viral dose in pfu/cell (plaque-forming units), 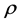and the population of non dividing cells that are infected, respectively. Let r denote the overall growth rate of the uninfected dividing and non-dividing cell population. We assume the rate of misrecognition (i.e., death of an uninfected cell) due to MHC-I upregulation 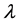is given by 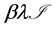for some fraction.

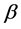Then the net rate of change of 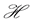with respect to is 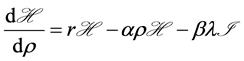where we assume a

linear model for the dependence of the rate of infection on the viral load level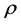, with 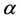being the fraction of viral load which is effectively translated into infection. Now if r is the growth rate of the uninfected dividing and non-dividing cell population, then 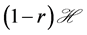is the size of the pool of cells which can be infected. The rate of

change of 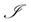with respect to is thus. In matrix-vector form, we have

For our purposes here, the only parameter of interest is the viral dose. We thus have the system

where

Let’s assume is a point where the survival curve oscillates. If you look at Figure 1, you can see several such candidates.

At such a point, approximate the system by the constant term. Near, we expect the dynamics of to be captured nicely by this approximation. This is a linear system of first order differential equations and the general solution is determined by the eigenvalues of the matrix. Our data on survival curves for WNV infections (see Section 4 and Figure 1) tells us that there should be oscillation in versus plot and hence, the characteristic equation for this system should exhibit complex roots with a negative real part. Then we would see a exponentially damped phase shifted cosine solution which would match the data. The characteristic equation is given by

This has roots

Note the discriminant D is given by and thus we have exponentially damped oscillating healthy cell populations if (this is easy to achieve as the viral load increases) and if. The discriminant function is therefore a complicated function of the parameters, , , r and, but it is easy to see that under some combinations of these parameters, D is indeed negative giving rise to damped oscillations near a value of. For example, we can show how for a large enough, these oscillations can arise. From [2] , we know. Let’s assume we have high upregulation,. We don’t expect the misrecognition rate to be very large, so let’s assume. If we plot the discriminant function versus the parameter for these values, we can see the results in Figure 2.

The survival model discriminant function can be negative leading to oscillations:, and upregulation is 9.

The figure shows us that the discriminant is negative in the range or so. Thus, for example, if, then as here and there are many choices of leading to oscillation as we have. Thus can vary enormously in value and give oscillations. We know is the fraction of viral load that is translated into infection and thus, if, we have oscillation can occur if. In a typical survival plot, we use the logarithm of, hence we could see oscillations near the value of. This simple model therefore suggests that we can have survival oscillations as we see in the data at a variety of viral loads. On the other hand, if if we decrease the upregulation to a smaller value such as, we see from Figure 3 that the range of giving rise to oscillation is substantially diminished. Hence, as the amount of upregulation decreases, there is a lesser chance of oscillation. Finally, we note that is upregulation further decreases to, all chance of oscillation is lost as seen in Figure 4. This calculation with a very simplified model of healthy cell versus viral load dynamics therefore suggests it is possible for there to be combinations of these parameters that lead to oscillations in the survival curve even at high viral dose. This implies that upregulation is the key factor leading to collateral damage and the unusual survival data we see.

3. Healthy Cell Approximations

When the immune system response causes healthy cells to be lysed, this is called collateral damage and in the case of West Nile virus infections, it has been discussed in [2] . We can use the damage model outlined there to shed insight in yet another way. We can rewrite the healthy cell update equation as

(1)

where at time t, is the uninfected cell population, is the population of newly infected cells and is the population of uninfected cells lyzed by T cells. The parameters and are the growth factor for uninfected cells and the resource limit for uninfected cells. Equation 1 suggests that satisfies the differential equation. We know there is collateral damage that depends on the level of upregulation and the initial dose of virus and that it leads to unusual survival curves. We suspect this is due to the presence of virus that hides in the dividing cells and hence is shrouded from immune system notice. Let’s try to make this idea more precise. There needs to be some sort of interaction between the new infections and the collateral damage that leads to these kinds of survival oscillations but it is hard to see it from the dynamics above. Taking a second derivative, we see. The coarse update model from [2] estimates collateral damage using

(2)

In Equation 2, N represents how we discretize our simulation universe of possible cells. We use about 10⁸ cells in the simulation (coding details are in [1] and the general derivations in [2] ) and use a three dimensional box of size 217 on a side to give us 10⁸ possible cells. We divide this universe of cells into larger cells or coarse cubes for computational ease in our simulations with and we let denote the collateral damage estimate in course cube i. We assume cells in a given coarse cube can upregulate due to the infection. In the simulation, the number of new infected cells that are not dividing and are removed in cube i is denoted by, where the subscript r indicates removal. Similarly, the number of new infected cells that are dividing and are removed in cube i is denoted by. In the simulation, we also keep track of the number of upregulation signals sent to the coarse cube in the variable. As the simulation progresses, the number of removed cells due to upregulation is dependent on how many times a cell receives an upregulation signal. The sum of the removals due to these events in stored in the variable for a given MHC-I upregulation level and coarse cube i. Finally, the term is the amount of random perturbation we use around the base values.

We let the fraction and the fraction be denoted by and, respectively. These are probably

small but for the moment think of as simply another parameter. Replace using the regression model and ignore the random perturbation term. Thus, we have

Further, ignore the slight modification due to the intercept term b giving

Next, assume this is true for all coarse cubes, giving

We think it is reasonable to assume that if the number of healthy cells increases, the amount of collateral damage will increase also. We also believe that the amount of collateral damage will depend on the level of the initial viral dose which we will call I. Hence, let’s assume the parameter is proportional to interaction between the initial dose and the cumulative amount of healthy cells present from time 0 to the current time t, and the initial viral dose I. Interactions are often modeled as products; hence, we assume

Next, assume this is true for all coarse cubes, giving the final model

We let denote the proportionality constant. The number of new infections, , should decrease if the proportion of healthy cells increases; we are assuming qualitatively that a healthier system resists infection. Over the course of an infection cycle of time T (for us 1440 15 minute time units or 15 days), the maximum amount of healthy cell impact is as is the resource allocation limit given by the homeostatic logistics growth law used to control cell population in the simulation [2] . This is similar to the idea of a life work: i.e. force times length of time the force is active, T, is a work done point of view. We think of this as the amount of life energy available for use by the infectious agent. Hence, the total amount of life energy possible minus the amount actually used currently is an estimate of what is available for infection. This amount is. Hence, modeling interaction of the amount of initial viral dose, upregulation level and available life energy as a product, we have

Let this new proportionality constant be denoted by. Combining, we have

Hence, we have and. Thus, an approximate dynamical model for the healthy cell level is given by the nonlinear second order model

We can solve this model numerically using the initial conditions and for two types of corrective terms. If, this adds to and if, we subtract from. This term should be close to a balance, hence, we will solve two problems with positive and negative values of. When, we call this a negative correction and the graph in Figure 5 shows increases past the usual resource allocation limit,. Of the other hand, if, we call this a positive correction and the graph shows the level decreases below the usual resource allocation limit. Now the term is going to change at each time step t rather than be constant as we have here and hence, the levels of will move up and down depending on the contribution of. Our aim with this graph is to show the positive and negative correction terms move the healthy level up and down which implies the possibility of the balance of new infection and collateral damage to shift so as to allow the healthy level to increase. Note, we can’t really see this possibility of an increase in from the original first order dynamics given by. It was important to pass to the second order dynamics which requires making additional assumptions. The survival data tells us as increases, sometimes the term becomes negative, allowing to increase. The exact dependence of this correction term on and I is, of course, quite complicated and difficult to tease out. We can get a little more insight by modifying our and assumptions a bit. As before, we still think it is reasonable to assume that if the number of healthy cells increase, the amount of

collateral damage will increase also. However, let’s now assume the amount of collateral damage will depend on both the level of the initial viral dose which we will call I and the upregulation level. We now assume the parameter is proportional to interaction between the initial dose of virus, I, the upregulation level, to some positive power p and the cumulative amount of healthy cells present from time 0 to the current time t. Again, modeling the interaction as a product, we have. Next, assume this is true for all coarse cubes, giving the final model. where we still let denote the proportionality constant. The number of new infections, , should decrease if the number of healthy cells increases and we still use our notion of life work. Hence, modeling interaction of the amount of initial viral dose to the positive power, upregulation level and available life energy as a product, we have

This is not necessarily true, but we want to show how assuming the dependence is not linear allows for behavior that is consistent with the measured survival data. Again, let this new proportionality constant be denoted by. Combining, we have

Hence, we have

Thus, an approximate dynamical model for the healthy cell level is given by the nonlinear second order model

Now, the sign of the correction is determined by the function. This function is zero when which implies. Hence, for this simple extension of our modeling of and, we see there is a change in the sign of the reinforcement term around. This lends further credence to the idea that there is a critical value of I for which we can increase implying a return to health even though the initial viral dose is large. Also, note it is the presence of the upregulation that plays a major role here.

So we can see that various assumptions about the dependencies of the new infection levels and collateral damage levels on and I lead to predictions of varying levels that can lead to the survival data we see. Determining these functional dependencies should be amenable to experimental protocols. However, here we will show that by constructing our simulation very carefully, we can see this behavior. Hence, the remainder of our discussion is to buttress our claims that our simulation results provide some validation for the decoy hypothesis.

4. Survival Models

In a survival experiment, a population of mice of size N is all infected with the same amount of virus, and the number of animals that die is determined. The amount of virus used is measured in plaque forming units (pfu). This determines the concentration of infectious virus by virtue of the number of areas of cell death in a cell monolayer in vitro. The experiment is then repeated, using N mice per group for a range of virus concentrations. If we did this for various pfu levels, we could then graph the number of mice that survive versus the virus concentration. Such a survival experiment is expensive to undertake, requiring many mice and hence, rarely done. With most viruses, a traditional survival experiment in which the virus is titrated in this way, gives a classical dose-response curve which progressively and smoothly decays down to a survival of 0 at high virus concentrations. WNV has a peculiar survival curve which was shown in Figure 1. Our simulations show similar results, although we use an artificial parameter in our simulations for the pfu level and in Figure 6. In this simulation, we modeled host infections in 18 groups using initial viral concentrations ranging from 100 to pfu. The raw results are shown in Table 1. In the table, you will note that there is an increase in all the measures of survival (Normalized Health, Survived, Survived 2 and Survived 3) where each measure attempts to estimate

host fatality in a different way. For a given viral dose, we compute many plots and each plot is terminated at a time, which may be substantially less than the final time which is usually 1440.

Normalized Health; First we calculate where in the simulation. This is the area under the health curve. Since the plot may terminate early, we also calculate the area. We then set the health value to be. Since the total number of healthy cells in the simulation is, we could think of maximum health as. One measure of damage is then to find the difference between maximum health and as calculated above. area of possible health between the set the damage value. We can calculate the lowest health value in the plot as follows: we find the smallest health value for the plot, and the time it occurred in the plot,. We then calculate a measure of how low the health of the host has become as

Hence, we adjust the low value of the plot by extending it over the full interval in the case the plot

terminates early. A measure of health is then. We can then average these values over all

the plots for this viral dose to find an average normalized health value.

Survived: If the health value we have calculated, exceeds, we count this as a survival for this level of virus dose. Since we have said a number of plots per viral dose, this allows us to count how many hosts at this viral dose survived.

Survived 2: We can also calculate another measure of survival. If the lowest health value, is very high, say larger than 0.99P, then we set a second measure of lowest health, to simply be the health. Otherwise, we set which is measuring how long the health stays above the minimum level over the full time of the simulation.

If the normalized smallest health level, exceeds some threshold, here 0.25, we count this plot as a survival.

Survived 3: The third way we can use to estimate survival is to calculate the time interval that the value lies below a threshold of P, here 0.9P. We can compute this time and call it as it is a sort of clipping of the actual plot. We can also calculate the area of the plot that lies below this threshold and call it a health window and denote it by. We then set another notion of damage to be the normalized value. If this value is greater than 0.65, we count this plot as a survival and update this measure of survival.

We show normalized health versus the logarithm of the infection level in Figure 6. In Figure 7, we plot all

three different survival measures versus the logarithm of the virus concentration but only for the range of viral dose where there is an increase in survival. We see the characteristic increase in survival with increasing viral load in all three measures as well as in the normalized health plot. We see in both simulation plots, survival sometimes increases with increasing virus concentration, in contrast to the data seen in most other viral infections.

5. Conclusion

We show the decoy hypothesis is a reasonable way to explain collateral damage and the existing survival data measured in WNV infections. In addition to the simulation results, we have also included simple arguments based on approximations that also show we can expect some sorts of oscillatory behavior in the level of healthy cells versus viral load. In Section 2, we let denote the population of uninfected dividing and non-dividing cells and, the population of infected non-dividing cells and assumed nonlinear interactions between them mediated by the viral load, the variable, and the MHC upregulation level, the variable. We showed there was reason to believe this dynamic model allowed for oscillations in the health level, such as we saw in the survival data. Then in Section 3, we use the simulation dynamics from [2] to develop an approximation to collateral damage in the model. This allowed us to develop a second order model for the size of the uninfected cell population, i.e., the healthy cells given by

from which we could also reason that oscillations in the survival rate could be expected. We then presented simulation results that supported these suggested behaviors. A more general model, [11] , can also be developed where we assume a large population of cells consisting of cells which are dividing and are infected, , cells which are not dividing but are still infected, , non infected cells, and non infected cells which will be removed due to auto immune action which we call, for collateral damage. We then assume all of these variables depend on the three parameters, , the IFN-g signal emitted by cells being lysed; the MHC-I upregulation factor, here the variable, and the free antigen level which here is the variable. Our work in this paper does not use the IFN-g signal, but with the IFN-g signal a more detailed analysis is possible and we can derive analytical equations predicting health and survival. Numerical results then also support the oscillations in survival we see in the data. The models we present here are based on the micro level one presented in [2] but the new model in [11] essentially uses a macro level approach. These WNV studies then suggest a more general model of autoimmune response which uses both micro and macro level reasoning [12] . We show there are self damage effects whenever the triggering agent’s effect on the host can be separated into two distinct classes of cell populations such as we see in the WNV infections where the two classes are the infected cells that are dividing and the infected cells that are not. As long the trigger acts differently in each population and this behavior is mediated by nonlinear interactions between two signaling agents which satisfy certain critical assumptions, there is collateral damage. All of these results posit the existence of collateral damage and it is also important to develop a model of how self damage occurs. This has been done in work that uses a new model of the immuno synapse and cytokine/chemokine signalling grammars to understand how a self damage can occur [13] .

Cite this paper

James K. Peterson,Alison M. Kesson,Nicholas J. C. King,1 1, (2016) Using a Collateral Damage Model to Explain Survival Data in West Nile Virus Infections. Advances in Microbiology,06,251-262. doi: 10.4236/aim.2016.64025

References