Advances in Microbiology
Vol.3 No.8A(2013), Article ID:40729,4 pages DOI:10.4236/aim.2013.38A002
Mathematical Modelling of the Micromicetes Colonies Growth Applying the Diffusion Equation
Ufa State Aviation Technical University, Ufa, Russia
Email: lia_87@rambler.ru
Copyright © 2013 Albina R. Idiyatullina et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 15, 2013; revised November 15, 2013; accepted November 22, 2013
Keywords: Mathematical Models; Micromicetes
ABSTRACT
We have studied the mathematical model of the growth of a micromycetes colony. The results of the numerical experiments have shown that the model given in the work quite adequately reflects the emergence of the ring structures in the micromycetes colonies.
1. Introduction
The attempts of mathematical modeling of biological structures and processes, alongside with the search for natural and experimental models to describe and investigate biological morphogenesis, i.e. emergence of elaborate structures in the development of microorganisms colonies, have been undertaken in mathematical biology for years.
In many biological systems, the mechanism of spatial structures formation is connected with the violation of stability of a homogeneous system. Mathematical models of such processes represent systems of the equations in the derivatives of a reaction-diffusion type.
Apart from the diffusive instability, an essential factor that can promote structuring is chemotaxis, i.e. the direct movement of cells along the chemical gradient.
A number of experiments have been described in literature where the formation of spatial structures in bacterial systems is observed, wherein both moving and stationary structures are possible.
For the first time, the research results of diffusion equation related to the growth of the substance amount were applied to the study of biological problems in the works by Kolmogorov A.N., Petrovsky I.G. and Piskunova H.C. [1]. The problem of populating the area with some species was also considered. There obtained a differential equation of a “reaction-diffusion” type (KPP equation).
Moving structures were described by Adler [2]. It has been established that bacteria locally inoculated into a growing medium can form spreading population waves. The reason of this phenomenon was explained, apparently, by the fact that in this case, bacteria chemotaxis to the gradients of substratum components plays a defining role.
The mathematical model of such a wave movement was offered by Keller and Segel in 1971 [3]:
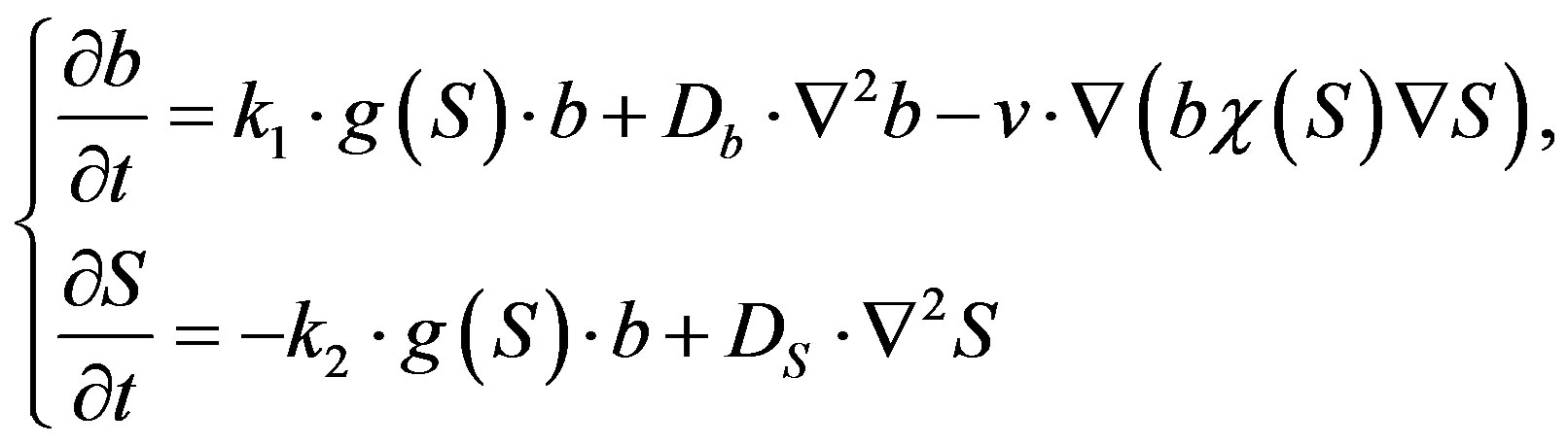
where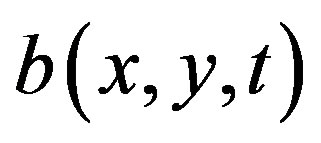 —is the bacteria density at time t and position (x,y),
—is the bacteria density at time t and position (x,y),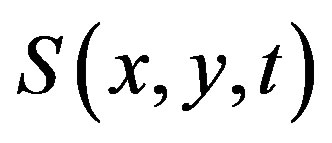 —is the concentration of the chemoattractant,
—is the concentration of the chemoattractant,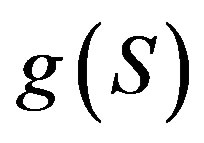 —is the specific growth rate of bacteria,
—is the specific growth rate of bacteria,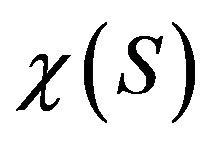 —is the function that indicates the sensitivity of bacterıa to the chemoattractant,
—is the function that indicates the sensitivity of bacterıa to the chemoattractant,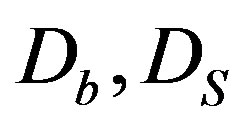 —are the coefficients of bacteria diffusion and a substratum, respectively,
—are the coefficients of bacteria diffusion and a substratum, respectively,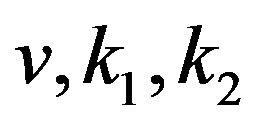 —are constants.
—are constants.
Keller Segel’s model and some of her modifications succeeded to describe the formation and distribution of hemotaksis Adler rings and various structuring processes in bacterial colonies during their interaction. It was also shown that bacterial population waves belong to a special class of autowaves.
2. Mathematical Modelling
The study of the processes of the motionless ring structures formation in the work of Polezhaev A.A. et al. [4] shows that there are, at least, two forms of bacteria in the growing colonies: rod-shaped mobile dividing cells and larger units of non-dividing cells. Mobile cells are located on peripheries, while units are located inside the colony, what causes concentric rings of the increased density. The formation of spatial structures is fixed as a result of transfer of dividing mobile bacteria to an anabiotic form, i.e. to a condition in which bacteria are non-dividing and immobile.
In a number of works [5-9] there has been offered a mathematical model for the description of ash value emergence in colonies of a micromycetes, where the process of colonies formation is considered as a phenomenon of self-organization caused by the diffusive instability. As the main hypothesis of such structures formation, the assumption of the metabolism products and their diffusion impact on a micromycetes colony was considered. The following system of the differential equations describing the distribution of concentration of a mycelium ( ), a substratum (S) and metabolism products (m) has been studied as a mathematical model:
), a substratum (S) and metabolism products (m) has been studied as a mathematical model:
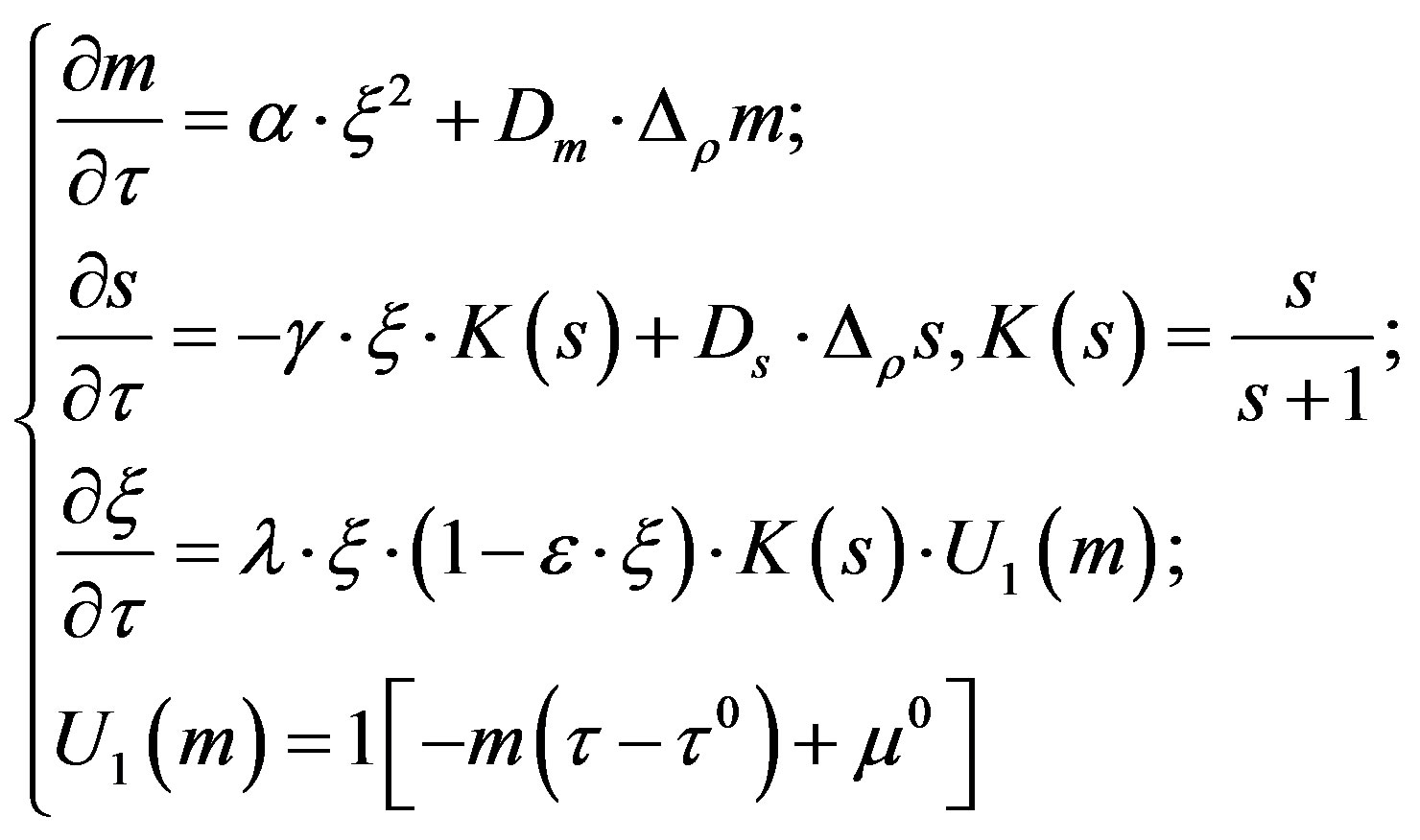
Here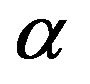 —is a large-scale coefficient of speed of metabolism products formation,
—is a large-scale coefficient of speed of metabolism products formation,
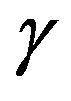 —speed of consumption of a substratum,
—speed of consumption of a substratum,
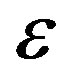 —maximum (resource) concentration of a mycelium,
—maximum (resource) concentration of a mycelium,
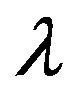 —specific growth rate of a mycelium concentration,
—specific growth rate of a mycelium concentration,
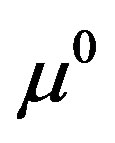 —threshold concentration of the metabolism products, defining the mycelium growth,
—threshold concentration of the metabolism products, defining the mycelium growth,
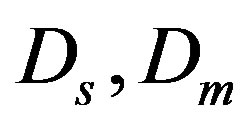 —coefficients of diffusion of metabolism products and a substratum,
—coefficients of diffusion of metabolism products and a substratum,
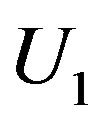 —functions of conditions1[x]—Hevisayd’s function (function of single jump),
—functions of conditions1[x]—Hevisayd’s function (function of single jump),
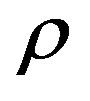 —relative radial coordinate,
—relative radial coordinate,
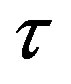 —time,
—time,
 —delay time of a mycelium response to the presence of metabolism products.
—delay time of a mycelium response to the presence of metabolism products.
The system was studied together with the boundary conditions of the second kind that correspond to a case of impenetrable external walls.
Authors of the article have carried out experimental observations of the formation of the spatial-temporal structures in the micromycetes colonies, as well as numerical experiments with the use of the given mathematical model. The results of these calculations describe the formation of such types of spatial distribution as wave (zone) structures and a continuous lawn in fungi colonies. The experimental data is well agreed with the mathematical model.
It has been, however, established long before [6] that the metabolism products can’t be the main reason for the ring structures emergence with the growth of micromycetes. On the other hand, a simple analysis of the mathematical model shows that the system of the differential equations doesn’t imply the distribution of mycelium concentration. The initial concentration of the mycelium covered only a part of radius of the initial crops, rather than the whole radius of a Petri cup, and the term corresponding to its diffusion was missing in the equation with the mycelium.
We have studied the following mathematical model of the growth of a micromycetes colony:
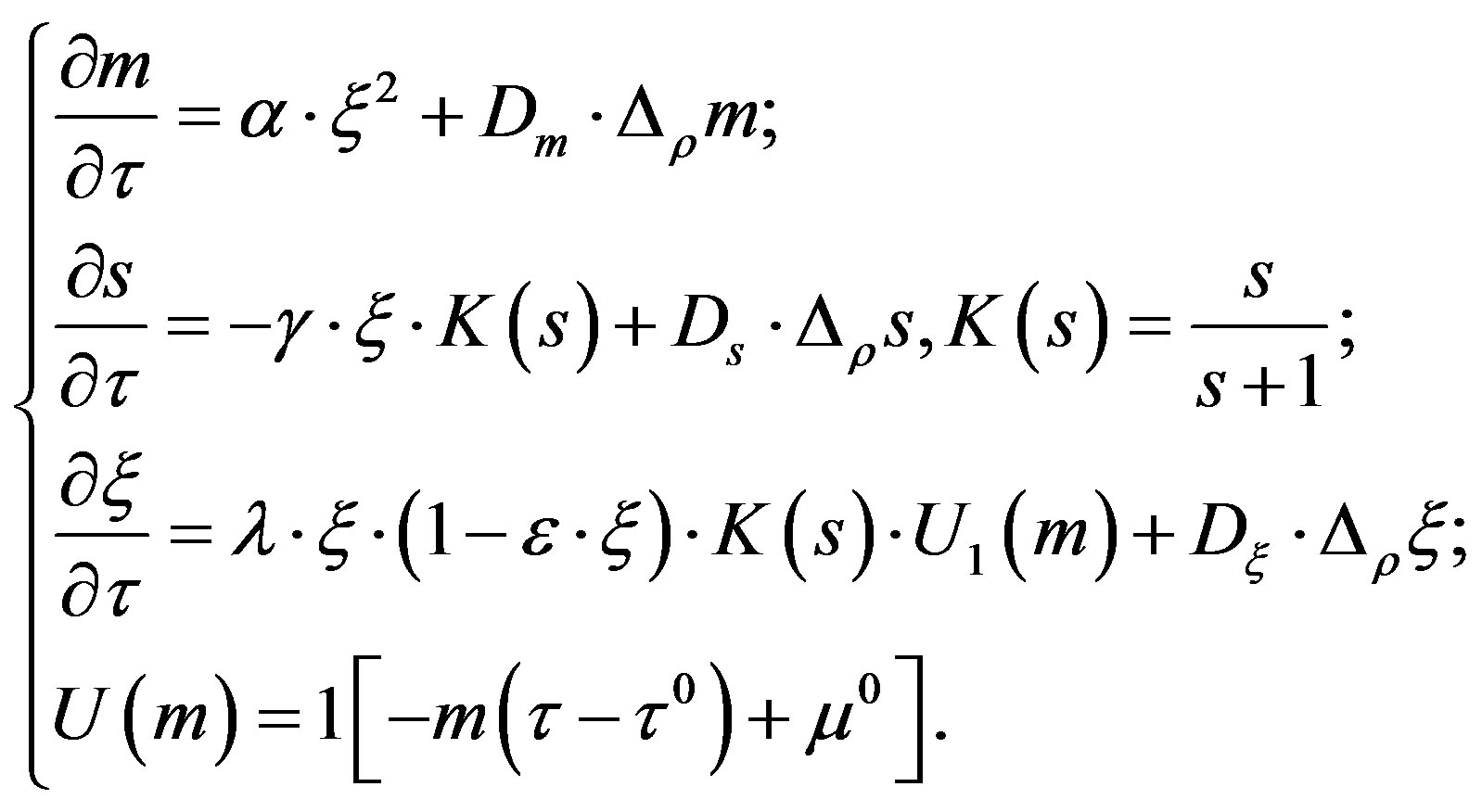
This system describes the following model experiment. The initial colony, representing a drop with the high or low number of cells, is placed into the Petri’s cup with a certain amount of the substratum. While consuming the substratum, the cells develop metabolism products.
In the fırst equation term 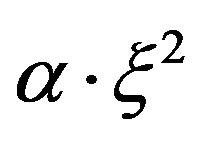 describes the growth of metabolism products m, which is proportional to a square concentration of the mycelium. The given dependence is obtained through the experimental data.
describes the growth of metabolism products m, which is proportional to a square concentration of the mycelium. The given dependence is obtained through the experimental data.
The term 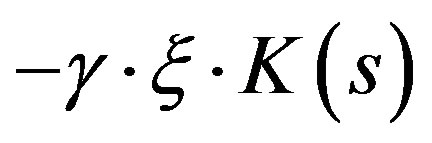 in the second equation reflects the reduction of the substratum concentration in proportion to mycelium growth taking into account the substratum exhaustion s.
in the second equation reflects the reduction of the substratum concentration in proportion to mycelium growth taking into account the substratum exhaustion s.
The composed 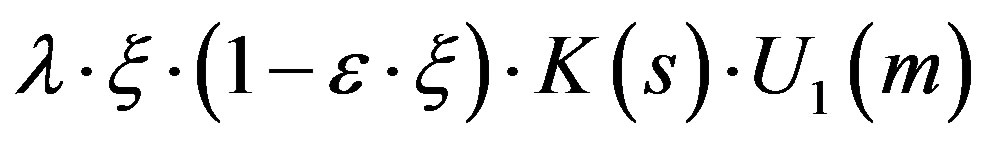 in the third equation is responsible for the formation of the mycelium. The mycelium growth is limited by the following factors:
in the third equation is responsible for the formation of the mycelium. The mycelium growth is limited by the following factors:
- the achievement of the limit (resource) concentration- the substratum exhaustion s- the development of metabolism products to the level of the concentration determined by a condition U1.
Together with the system of the equations the following entry conditions are considered:

as well as the boundary conditions of the second kind, meeting the requirements of the external walls impermeability:
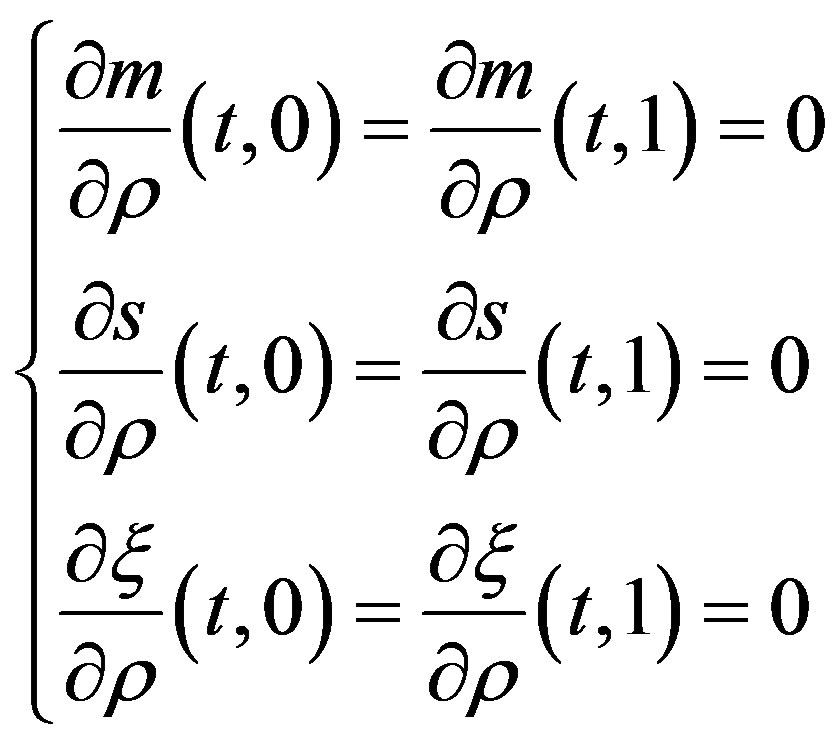
3. Numerical Modelling
To determine the operating parameters the numerical experiments with the use of the offered mathematical model were carried out. As a basic vector of parameters we chose the following:
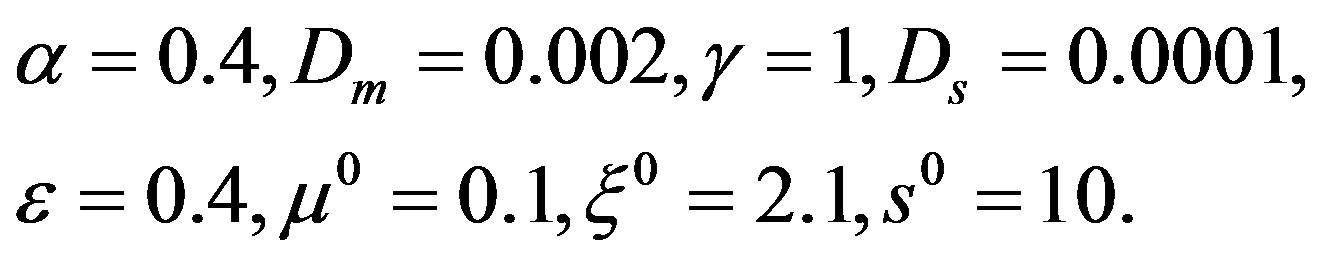
When fixing the coordinates of a vector the variation of system parameters were made: 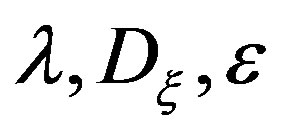 and
and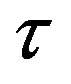 .
.
The numerical modeling of the system showed the following results (Figure 1).
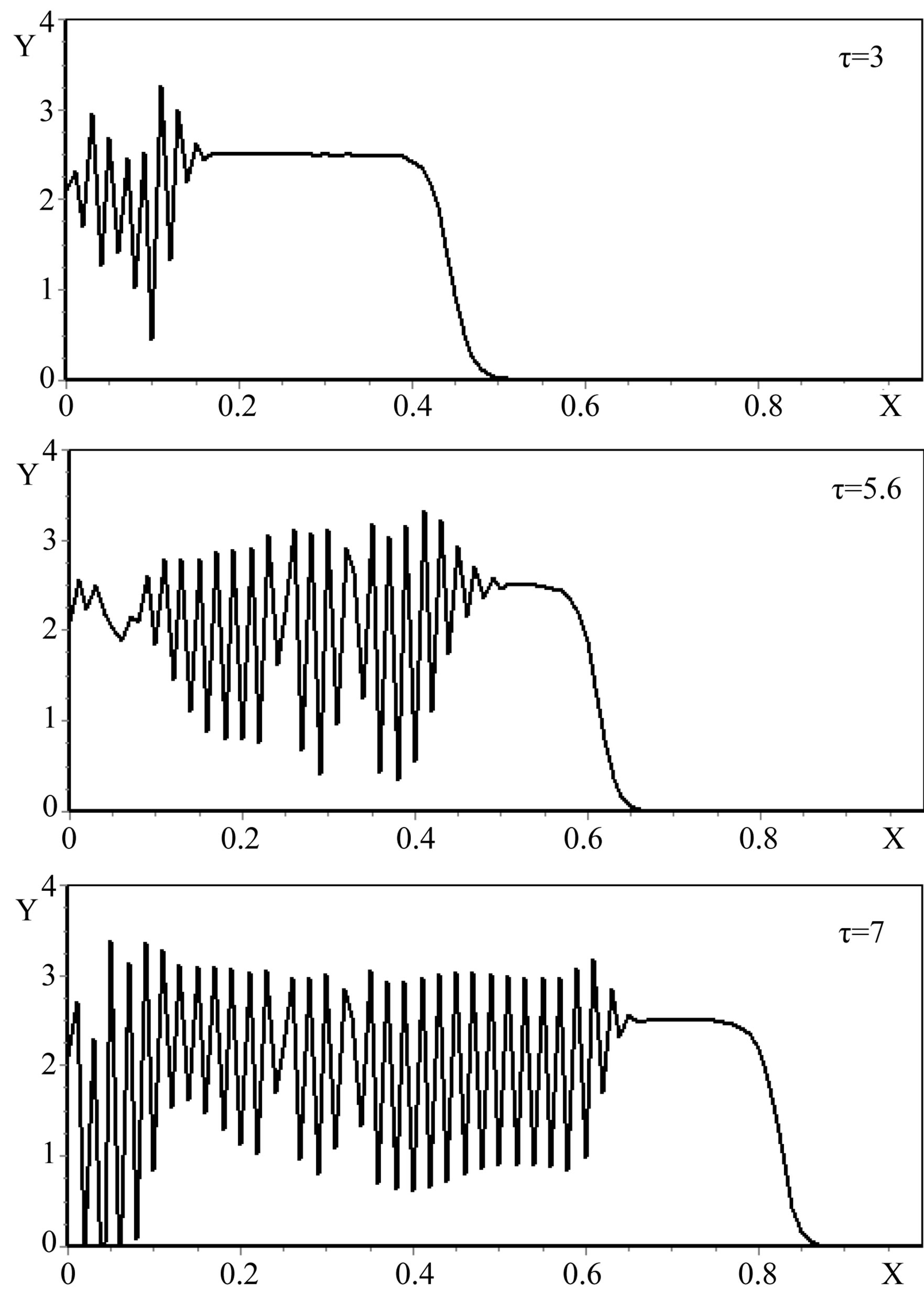
Figure 1. The dynamics of a colony growth with the formation of wave structures. The model parameters are λ = 4, α = 0.4, Dξ = 0.01, Dm = 0.002, γ = 1, Ds = 0.0001, ε = 0.4, μ0 = 0.1.
The analysis of the numerical modeling results showed that the most significant factors of the increase in a gradient of the mycelium concentration are the increase λ (Figure 2), and the decrease of 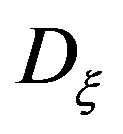 (Figure 3) and ε (Figure 4).
(Figure 3) and ε (Figure 4).
The parameters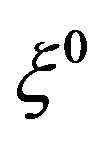 ,
, 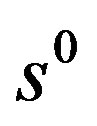 in the main only affect the amplitude of the oscillations of the mycelium. In the considered period of time, when the substrate is still little used up, the diffusion of the substrate due to the smallness of the diffusion coefficient
in the main only affect the amplitude of the oscillations of the mycelium. In the considered period of time, when the substrate is still little used up, the diffusion of the substrate due to the smallness of the diffusion coefficient 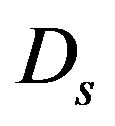 also no significant effect on the dynamics of the process.
also no significant effect on the dynamics of the process.
The process of colonies formation in time has also been tracked. Figure 1 demonstrates the dynamics of a colony growth, stages of consecutive formation of the large-scale ring structures, obtained as a result of numerical modeling.
Upon exhaustion of the resources in the equations system under the research, the steady state will be reached, where the concentration of the mycelium, the substratum and the metabolism ceases to change. The following differential equations have been obtained:
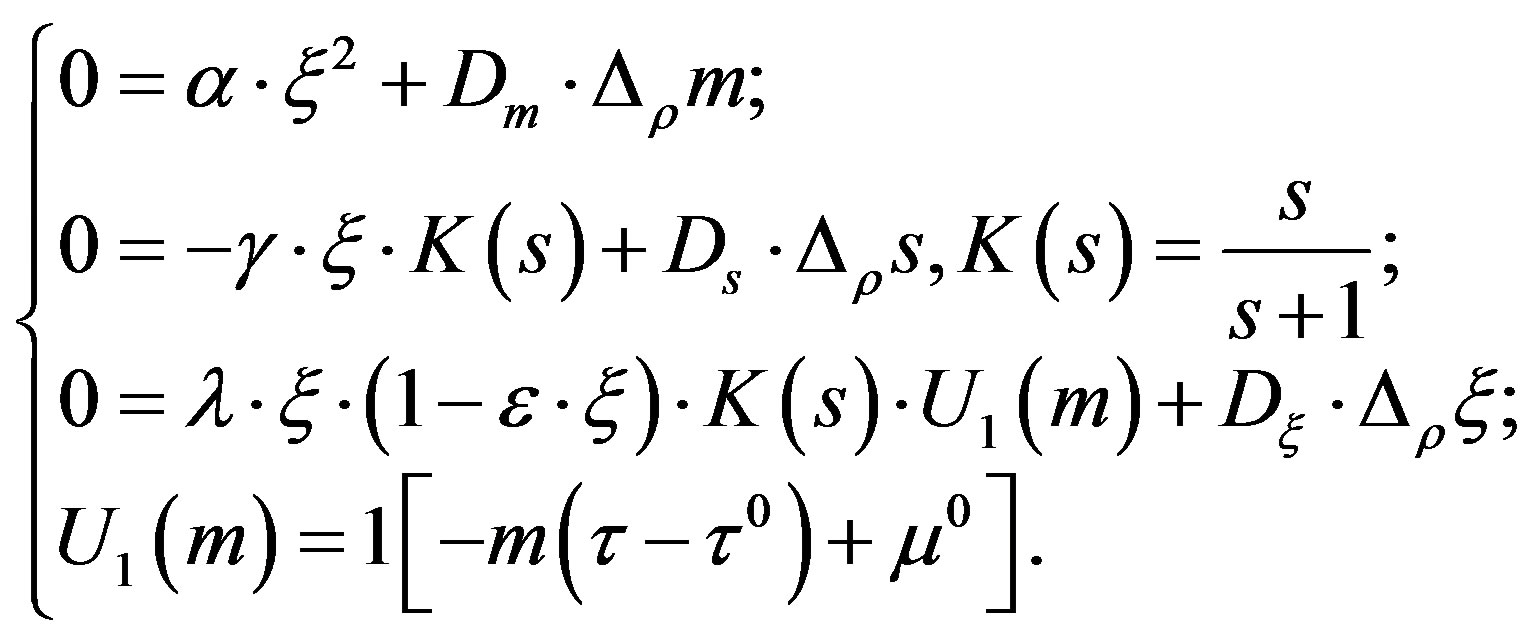
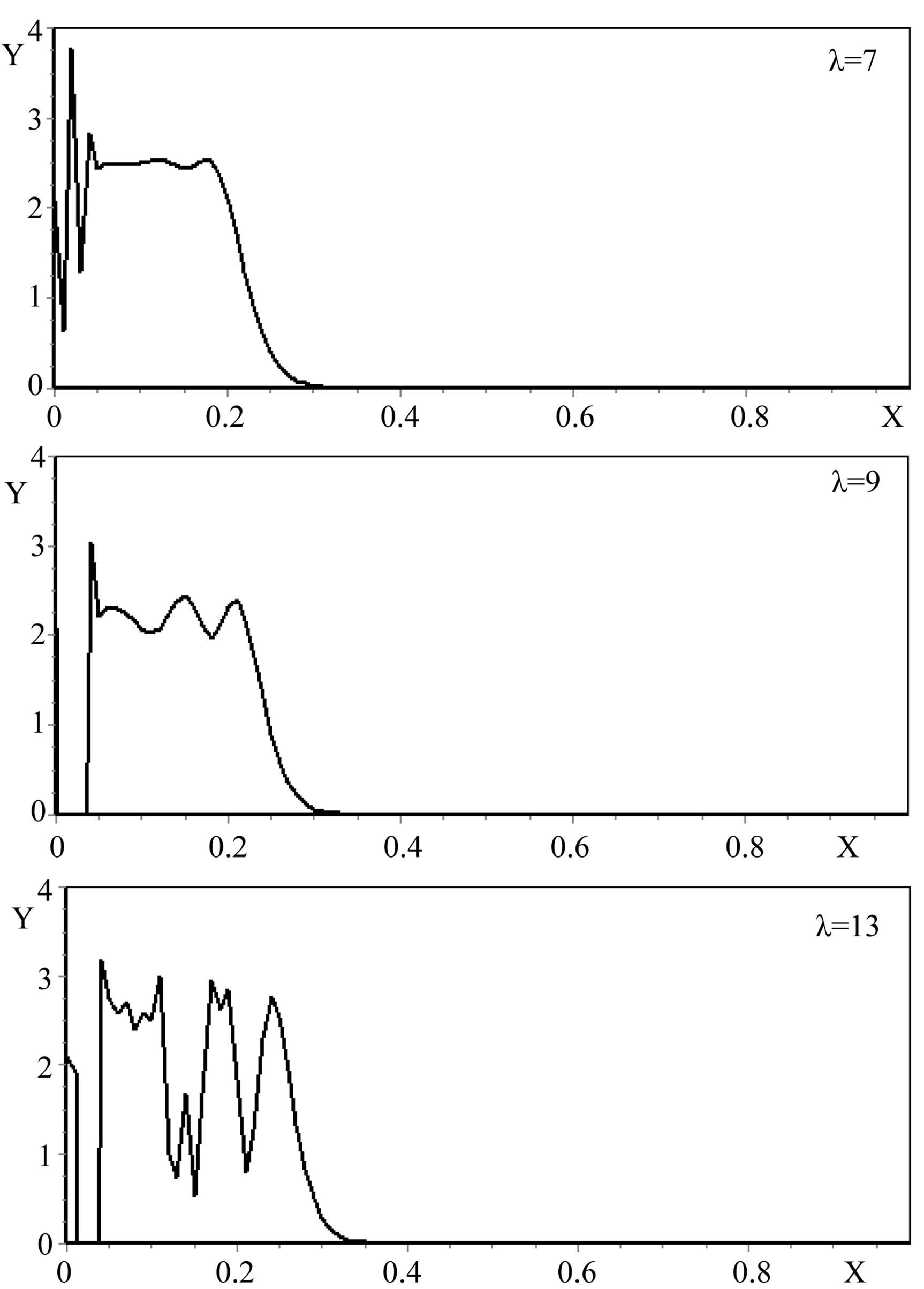
Figure 2. The self-organization form of a micromycetes colony at various values of size λ.
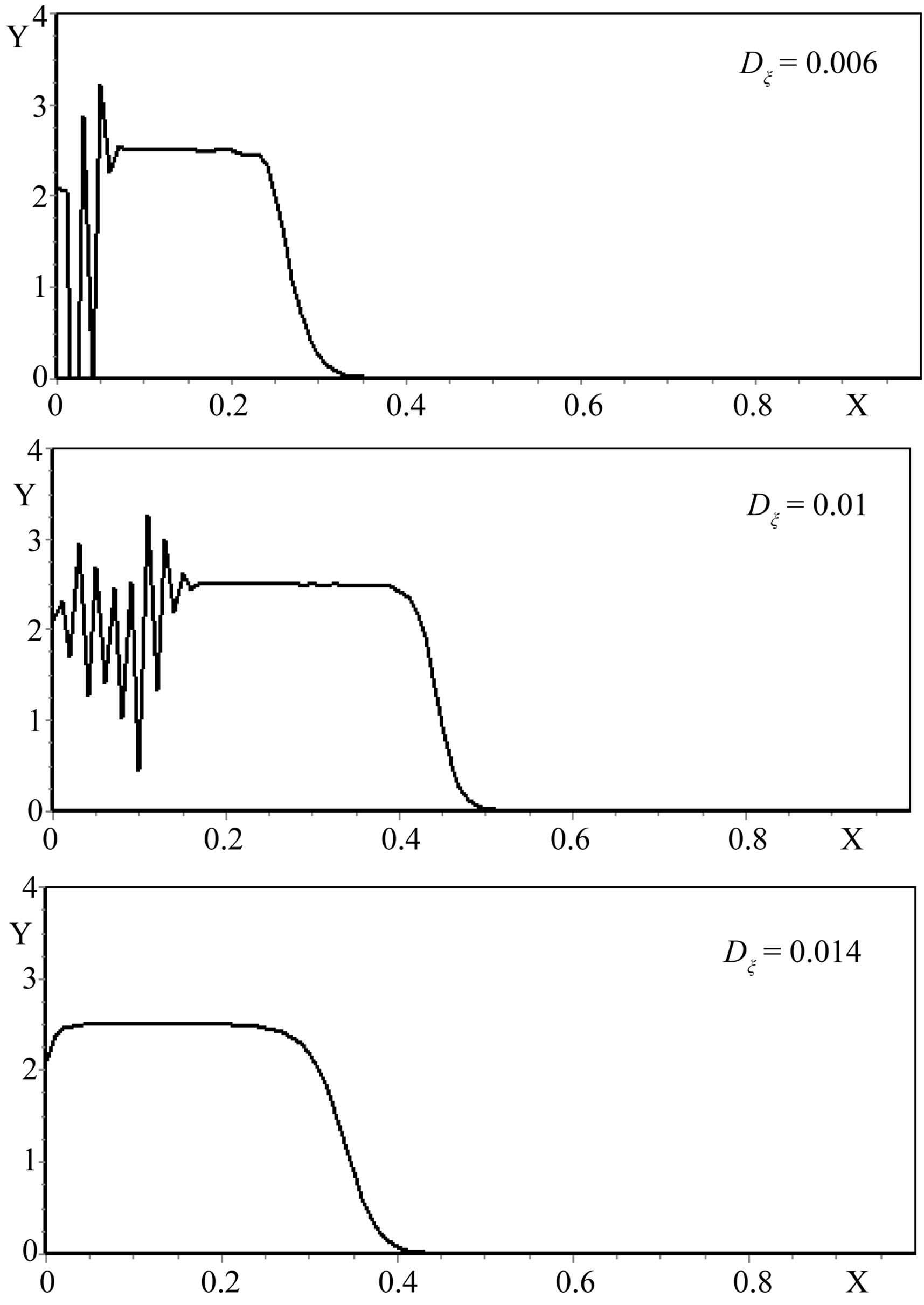
Figure 3. The self-organization form of a micromycetes colony at various values of the size Dξ.
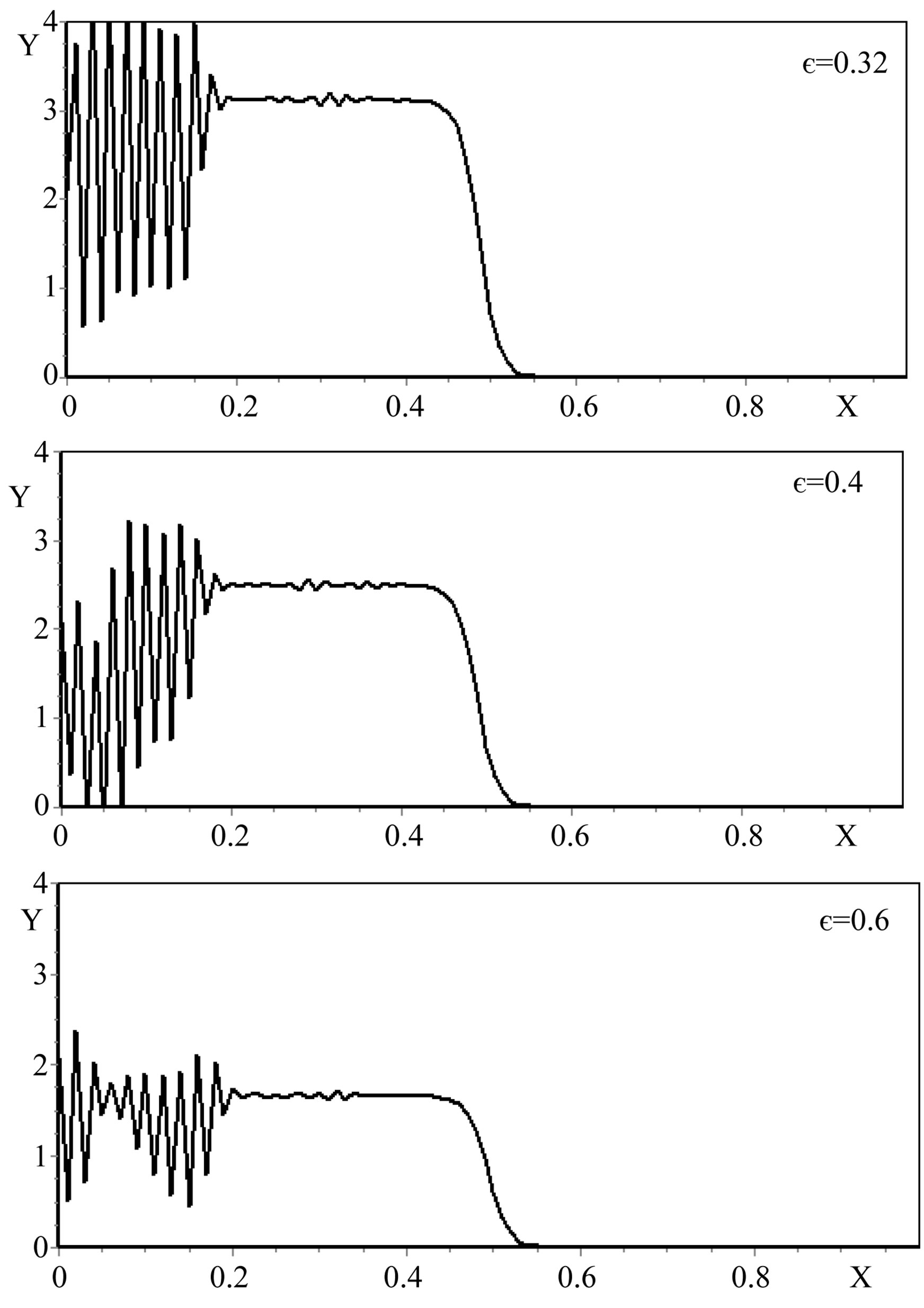
Figure 4. The self-organization form of a micromycetes colony at various values ε.
4. Conclusion
Thus, the results of the numerical experiments have shown that the model given in the work quite adequately reflects the emergence of the ring structures in the micromycetes colonies. By means of variation of the model parameters, we succeeded to get the structures given in the work of Bulyanitsa A.L. et al. [7].
REFERENCES
- A. N. Kolmogorov, I. G. Petrovsky and N. S. Piskunov, “Research of the Equation of the Diffusion Connected to Increase of Quantity of Substance, and Its Application to One Biological Problem,” Bulletin of the Moscow State University, Vol. 1, No. 6. 1937, pp. 1-26.
- J. Adler, “Chemotaxis in Bacteria,” Science, Vol. 153, No. 3737, 1966, pp. 708-716. http://dx.doi.org/10.1126/science.153.3737.708
- E. F. Keller and L. A. Segel, “Model for Chemotaxis,” Journal of Theoretical Biology, Vol. 30, No. 2, 1971, pp. 225-234. http://dx.doi.org/10.1016/0022-5193(71)90050-6
- A. A. Polezhaev and M. O. Ptitsyn, “The Mechanism of Emergence of Existential Orderliness in Bacterial Systems,” Biophysics, Vol. 35, No. 2, 1990, pp. 302-306.
- A. L. Bulyanitsa, E. V. Bogomolova, E. Yu. Bystrov, V. E. Kurochkin and L. K. Panin, “Model of Formation of Ring Structures in Colonies of Mitselialny Fungi,” The Magazine of the General Biology, Vol. 61, No. 4, 2000, pp. 400-411.
- A. L. Bulyanitsa and V. E. Kurochkin, “Research of Processes of Ordering in Open Systems (on the Example of Evolution of a Colony of Imperfect Mitselialny Fungi),” Scientific Instrument Making, Vol. 10, No. 2, 2000, pp. 43-49.
- A. L. Bulyanitsa, E. Yu. Bystrov, V. E. Kurochkin, L. K. Panin and E. V. Bogomolova, “Influence of Coefficient of Diffusion of Metabolites on Ordering Processes in Colonies of Imperfect Mitselialny Fungi,” Scientific Instrument Making, Vol. 10, No. 4, 2000, pp. 44-47.
- E. O. Tsvetkova, A. L. Bulyanitsa, V. E. Kurochkin, L. K. Panin and E. V. Bogomolova, “Influence of Adaptation Ability on Casting Processes in Colonies of Mitselialny Fungi,” Scientific Instrument Making, Vol. 11, No. 4, 2001, pp. 76-79.
- A. L. Bulyanitsa, “Phase Transitions in Colonies of Imperfect Mitselialny Fungi,” Scientific Instrument Making, 2004, Vol. 14, No. 3, pp. 97-101.

