ABSTRACT

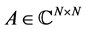In this paper, we propose DQMR algorithm for the Drazin-inverse solution of consistent or inconsistent linear systems of the form where is a singular and in general non-hermitian matrix that has an arbitrary index. DQMR algorithm for singular systems is analogous to QMR algorithm for non-singular systems. We compare this algorithm with DGMRES by numerical experiments.

Keywords:

Singular Linear Systems, DGMRES Method, Quasi-Minimal Residual Methods, Drazin-Inverse Solution, Krylov Subspace Methods

1. Introduction

Consider the linear system

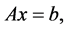(1)

where is a singular matrix and 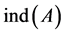is arbitrary. Here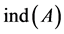, the index of A is the size of the largest Jordan block corresponding to the zero eigenvalue of A. We recall that the Drazin-inverse solution of (1) is the vector, where 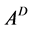is the Drazin-inverse of the singular matrix A. For the Drazin-inverse and its properties, we can refer to [1] or [2] . In the important special case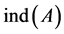, this matrix is called the group inverse of A and denoted by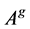. The Drazin-inverse has various applications in the theory of finite Markov chains [2] , the study of singular differential and difference equations [2] , the investigation of Cesaro-Neumann iterations [3] , cryptography [4] , iterative methods in numerical analysis, [5] [6] , multibody system dynamics [7] and so forth. The problem of finding the solution of the form 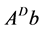for (1) is very common in the literature and many different techniques have been developed in order to solve it.

In [6] [8] [9] [10] [11] , authors presented some Krylov subspace methods [9] to solve singular linear system with some restriction. However, the treatment of singular linear inconsistent system by Krylov subspace has been proved extremely hard. In [12] , Sidi had not put any restrictions on the matrix A and the system (1). In his paper, the spectrum of A can have any shape and no restrictions are put on the linear system (1). The only assumption is that 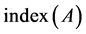is known. Although the 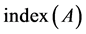of A is overestimated, the method is valid.

In [12] , Sidi proposed a general approach to Krylov subspace methods to compute Drazin-inverse solution. In addition, he presented several Krylov subspace methods of Arnoldi, DGCR and Lancoze types. Furthermore, in [13] [14] , Sidi has continued to drive two Krylov subspace methods to compute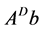. One is DGMRES method, which is the implementation of the DGCR method for singular systems which is analogues to GMRES for non-singular systems. Other is DBI-CG method which is Lanczos type algorithm [13] . DGMRES, like, GMRES method, is a stable numerically and economical computationally, which is a storage wise method. DBI-CG method, also like BI-CG for non-singular systems, is a fast algorithm, but when we need a high accuracy, the algo- rithm is invalid. DFOM algorithm is another implementation of the projection method for singular linear systems is analogues to Arnoldi for non-singular systems. DFOM algorithm may be less accurate but faster than DGMRES, and more precise and slower than DBI-CG [15] .

In the present paper, the Drazin-Quasi-minimal residual algorithm (DQMR here- after) is another implementation of the projection method for singular linear systems is analogues to Lanczos algorithm for non-singular systems. DGMRES algorithm, in prac- tice, cannot afford to run the full algorithm and it is necessary to use restart. For dif- ficult problems, in most cases, this results in extremely slow convergence, While DQMR algorithm can be implemented using only short recurrences and hence it can be com- puted with little work and low storage requirements per iteration.

The outline of this paper is as follows. In Section 2, we will provide a brief of sum- mary of the review of the theorem and projection method in [12] which is relevant to us. We shall discuss the projection methods approach to solve (1) in general and DQMR particular. In Section 3, we will drive the DQMR method. We design DQMR when we set 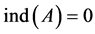throughout, DQMR reduces to QMR. In this sense, DQMR is an extension of QMR that archives the Drazin-inverse solution of singular systems. In Sec- tion 4, by numerical examples, we show that the computation time and iteration number of DQMR algorithm is substantially less than that of DGMRES algorithm. Section 5 is devoted to concluding remarks.

2. Some Basic Theorem and Projection Methods for A^Db

The method we are interested in starts with an arbitrary initial vector 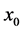and generate sequences of vector according to

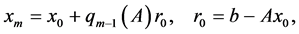(2)

where is a polynomial in of degree at most, given by

(3)

Let us define

(4)

We call the residual polynomial since

(5)

Note that

(6)

The condition (6) is due to Eiermann et al. [5] .

For convenience we denote by the class of polynomials of degree at most m and define

(7)

Thus, the polynomial described above is in.

The projection methods of [12] are now defined by demanding that the vector to be orthogonal to a given W subspace of dimension. In addition, If we denote by W the matrix whose columns span the subspace W, then this ortho- gonality demand is equivalent to. As we have from (4), amounts to the requirement that satisfy the linear system

(8)

where and are given by

(9)

We see that unique solution for c exists provided det, and when it does we have.

As we choose different W, we have a different algorithm: for DGMRES, we choose for DBI-CG, we choose

In this paper, for DQMR, we choose

We will mention several definitions and theorems, which have projection method converge below.

We will denote by the direct sum of the variant subspaces of A corresponding to its non-zeros eigenvalues, and by, its invariant subspaces corresponding to its zeros eigenvalue. Thus, is, the range of, and is, the null space of. So every vector in can be expressed as the sum of two vector, one in and other in.

Definition 1 [12] . Let A be singular and, and let be given. Then a polynomial will be called the minimal a―incomplete polynomial of A with respect to the vector if and m is the smallest possible one so that

The following theorems will ensure the success of projection method.

Theorem 1 [12] . exists and is unique. Furthermore, its degree m satisfies, where q is the degree of the minimal polynomial of A with respect to.

The following result that is the justification of the above-mentioned projection approach is Theorem 4.2 in [12] .

Theorem 2 Let, where and, are the initial vector in the projection method to compute. Moreover, Let also the minimal a―incomplete polynomial of A with respect to, and let m be its degree. Finally, let be the vector generated by the projection method through (2)-(8) with. Then.

Obviously, of Theorem 2 if, the projection method will terminate successfully in a finite number of steps, this number being at most N. If we pick, which also forces, they produce the Drazine-inverse solution for (1) upon termination.

Theorem 3 [14] . The vector exists uniquely and unconditionally for all, being the degree of the minimal a-incomplete polynomial of A with respect to. Furthermore, with and for all m.

3. DQMR Algorithm

In this section, we will introduce a different implementation of projection method. The algorithm is analogous to QMR algorithm. We must note that in spite of the analogy, DQMR seems to be quite different from QMR, which is for non-singular systems.

As, we start with, the lanczos

algorithm [16] generates two sequences of vectors and that satisfy

(10)

where they are clear that and denote the Krylov subspaces

respectively.

If we define that matrix by

then, we can write for

Therefore, it is obvious that we need to determine. Since we have

(11)

where.

Moreover, provided that, from (11) we can write

(12)

Note that. Since the vectors are linearly inde- pendent when, we have. Since, and

, we also have that. In other words,

has full rank. In additon, if we apply (12) to. Provided that, we have:

Consequently, provided, from (11) we can write:

and since, where, hence

If the column vectors of were orthonormal, then we would have:

as in GMRES. Therefore, a least, squares solution could be obtained from the krylove space by minimizing over. In the Lanczos algorithm, the’s are not orthonormal. However, it is still a reasonable idea to minimize the function

over and compute the corresponding approximate solution. The resulting solution is called the Drazin-Quasi-minimal residual (hereafter DQMR) approximation. Since is a tridiagonal matrix, Therefore, the is a matrix with diagonal to form (12).

Similar to [14] , can be obtained as a simple update of by first appending a row of zeros at the bottom of and following that by appending the -vector as the column as follows.

Let us define

(13)

(14)

where also for each.

Since is tridiagonal matrix we have:

where, certainly, , denotes the k-dimensional (column) zeros vector, and that is scalar.

Supposed that (15)

(16)

From [14] , we have: (17)

Equation (16) can be simplified as follows:

(18)

By using the Hadamard product Equation (18) is reduced. For this purpose, we first introduce the concepts of Hadamard matrix product.

Definition 2 Let A and B be matrices with entries in C. The Hadamard product of A and B is defined by as follows

Let us denote

Now, we can be simplified (18) as follows

(19)

For solution system

(20)

We must reduce the band matrix, , into upper triangular by using Givens rotation. matrix has bandwidth. To reduce the matrix to a upper triangular matrix we need to Givens rotations matrix. We denote with right-hand side (20), and we multiply both sides of (20) from left by Givens rotations. To update the mth column of matrix, we must first multiply the previous Givens rotations by this column and then we annihilate the main subdiagonal elements with appropriate rotations. It should be noted that number of the previous rotations is, and the number of the rotations to annihilate the main subdiagonal elements is. Finally, the mth end step we have an upper triangular matrix as follows

(21)

Generally, if we define the product of matrices, then

where be the Givens matrices use to transform into an upper triangular and the vector of. Finally , the approximate solution is given by

where and are obtained by removing the row of the matrix and right-hand side. The approximation solution can be updated at each step by the relation,

(22)

Since if we assume, then we have:

Consequently,

and

where is the last column of. Therefore, it can be written

or

(23)

Thus, can be updated easily at each step, via the relation (23) using.

This gives the following algorithm, which we call the Drazin-QMR for Drazin- inverse solution of singular nonsymmetric linear equations.

Algorithm 4.1 DQMR Algorithm

as in ( [17] , Algorithm 7.1).

(15).

13. EndFor.

16. End Do.

4. Numerical Examples

In this section, we will compute the linear system by discretization Poisson equation with Neumann boundary conditions:

This linear system has also been computed by Sidi [14] for testing DGMRES algorithm. The problem has also been considered by Hank and Hochbruck [18] for testing the Chebyshev-type semi-iterative method. The numerical computations are performed in MATLAB (R213a) with double precision. The results were obtains by running the code on an Intel (R) Core (TM) i7-2600 CPU Processor running 3.40 GHz with 8 GB of RAM memory using Windows 7 professional 64-bit operating system. The initial vector is the zero vector. All the tests were stopped as soon as

Let M be an odd integer, we discretize the Poisson equation on a uniform grid of mesh size via central differences, and then by taking the unknowns in the red-black order we obtain the system, where the non- symmetric matrix A is as follows

(24)

Here, I and 0 denote, respectively, the identity and zero matrices and the matrices and are given by

The numerical experiment was performed for.

It should be noted A is singular with 1D null space spanned by the vector . Furthermore, , as mentioned in [13] [14] [15] [18] . Even if continues problem has a solution, the discretized problem need not be consistent. In the sequel we consider only the Drazin-inverse solution of the system for arbitrary right side b, not necessarily related to f and.

We first construct a consistent system with the known solution via, where. Then we perturb, the right-hand side of , with a constant multiple of the null space vector e and we obtain the right-hand side

Consequently the system is solved for x. The perturbation para-

meter is selected as 10⁻² in our experiments. The solution we intend to obtain is the vector, whose components are zeros except

In Table 1, Table 2, we give the number of iterations (Its), the CPU time (Time)

required for convergence, the relative error (RE), for the DGMRES and DQMR methods. As shown in Table 1, Table 2 the DQMR algorithm is effective and less expensive than the DGMRES algorithm.

5. Conclusion

In this paper, we presented a new method, called DQMR, for Drazin-inverse solution of singular nonsymmetric linear systems. The DQMR algorithm for singular systems is analogous to the QMR algorithm for non-singular systems. Numerical experiments indi- cate that the Drazin-inverse solution obtained by this method is reasonably accurate, and its computation time is less than that of solution obtained by the DGMRES method. Thus, we can conclude that the DQMR algorithm is a robust and efficient tool to com- pute the Drazin-inverse solution of singular linear systems.

Acknowledgements

First, we would like to thank professor F. Toutounian for her comments that improved our results. Second, we thank the editor and the referees for their carefully reading and useful comments.

Cite this paper

Ataei, A. (2016) A QMR-Type Algorithm for Drazin-Inverse So- lution of Singular Nonsymmetric Linear Sys- tems. Advances in Linear Algebra & Matrix Theory, 6, 104-115. http://dx.doi.org/10.4236/alamt.2016.64011

References