Advances in Linear Algebra & Matrix Theory
Vol.4 No.2(2014), Article
ID:45914,8
pages
DOI:10.4236/alamt.2014.42005
On the Spectral Characterization of H-Shape Trees
Shengbiao Hu
Department of Mathematics, Qinghai Nationalities University, Xining, China
Email: shengbiaohu@aliyun.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 March 2014; revised 7 April 2014; accepted 14 April 2014
ABSTRACT
A graph G is said to be determined by its spectrum if any graph having the same spectrum as G is isomorphic to G. An H-shape is a tree with exactly two of its vertices having maximal degree 3. In this paper, a formula of counting the number of closed 6-walks is given on a graph, and some necessary conditions of a graph Γ cospectral to an H-shape are given.
Keywords:Spectra of Graphs, Cospectral Graphs, Spectra Radius, H-Shape Trees, Determined by Its Spectrum

1. Introduction
Let 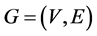 be a simple undirected graph with vertex set
be a simple undirected graph with vertex set  and edge set E. Let
and edge set E. Let  be the adjacency matrix of G. Since
be the adjacency matrix of G. Since  is a real symmetric matrix, its eigenvalues must be real, and may be ordered as
is a real symmetric matrix, its eigenvalues must be real, and may be ordered as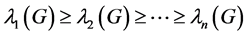 . The sequence of n eigenvalues is called the spectrum of G, the largest eigenvalue
. The sequence of n eigenvalues is called the spectrum of G, the largest eigenvalue 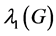 is often called the spectral radius of G. The characteristic polynomial of
is often called the spectral radius of G. The characteristic polynomial of 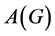 is called the characteristic polynomial of the graph G and is denoted by
is called the characteristic polynomial of the graph G and is denoted by .
.
Two graphs are cospectral if they share the same spectrum. A graph G is said to be determined by its spetrum (DS for short) if for any graph H,  implies that H is isomorphic to G.
implies that H is isomorphic to G.
Determining what kinds of graphs are DS is an old problem, yet far from resolved, in the theory of graph spectra. Numerous examples of cospectral but non-isomorphic graphs are reported in literature [1] . However, there are few results known about DS graphs. For the background and some recent surveys of the known results about this problem and related topics, we refer the reader to [2] -[6] and references therein.
Because the kind of problems above are generally very hard to deal with, some more modest ones suggested by van Dam and Haemers [2] , say, “Which trees are DS?”, this problem is also very hard to deal with, because we know a famous result of Schwenk [7] , which says that almost all trees have non-isomorphic cospectral mates.
A T-shape 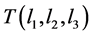 is a tree with exactly one of its vertices having maximal degree 3 such that
is a tree with exactly one of its vertices having maximal degree 3 such that , where
, where  is the path on
is the path on 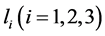 vertices, and v is the vertex of degree 3. More recently, Wang proved that T-shape tree
vertices, and v is the vertex of degree 3. More recently, Wang proved that T-shape tree  is DS; Wang and Xu [6] proved that T-shape tree
is DS; Wang and Xu [6] proved that T-shape tree 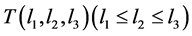 is DS iff
is DS iff  for any positive integer
for any positive integer .
.
An H-shape is a tree with exactly two of its vertices having maximal degree 3. We denote by  is an H-shape tree such that
is an H-shape tree such that  , and
, and 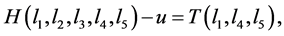
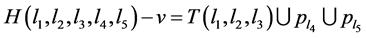 , where u and v are the vertices of degree 3.
, where u and v are the vertices of degree 3.
In this paper, we give a formula of counting the number of closed 6-walks on a graph, and give some necessary conditions of a graph Γ cospectral to an H-shape.
2. Some Lemmas
In the section, we will present some lemmas which are required in the proof of the main result.
Lemma 2.1 [8] The characteristic polynomial of a graph satisfies the following identities:
1)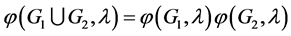 2)
2) 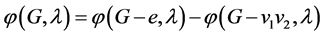 if e = v1v2 is a cut-edge of G.
if e = v1v2 is a cut-edge of G.
where 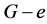 denotes the graph obtained from G by deleting the edge e and
denotes the graph obtained from G by deleting the edge e and  denotes the graph obtained from G by deleting the vertices v1, v2 and the edges incident to it.
denotes the graph obtained from G by deleting the vertices v1, v2 and the edges incident to it.
Lemma 2.2 [1] Let Cn, Pn denote the cycle and the path on n vertices respectively. Then

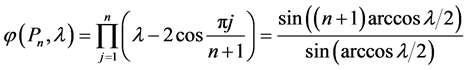
Let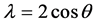 , set
, set , we get
, we get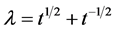 , it is can be write the characteristic polynomial of Cn, Pn in the following form [6] :
, it is can be write the characteristic polynomial of Cn, Pn in the following form [6] :
 (1)
(1)
 (2)
(2)
Lemma 2.3 [4] [9] Let 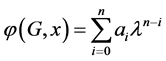 be the characteristic polynomial of graph G with n vertices, then the coefficient of λn−i is
be the characteristic polynomial of graph G with n vertices, then the coefficient of λn−i is
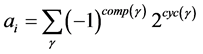 (3)
(3)
where a0 = 1 and the sum is over all subgraphs γ of G consisting of disjoint edges and cycles, and having i vertices. If γ is such a subgraph then comp(γ) is the number of components in it and cyc(γ) is the number of cycles.
Lemma 2.4 [2] [10] Let G be a graph. For the adjacency matrix, the following can be obtained from the spectrum.
1) The number of vertices.
2) The number of edges.
3) Whether G is regular.
4) Whether G is regular with any fixed girth.
5) The number of closed walk of any length.
6) Whether G is bipartite.
3. Main Results
The total number of closed k-walks in a graph G, denoted by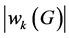 .
.
Lemma 3.1 ([6] p. 657) Let G be a graph with e edges, xi vertices of degree i, and y 4-cycles. Then
 (4)
(4)
Lemma 3.2 Let Γ be a graph with n vertices. If Γ cospectral to an H-shape and Γ ≠ Wn, then 1) Γ have the same degree sequences as the H-shape tree or Γ have the degree sequences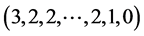 .
.
2) Γ contains no 4-cycles.
Proof. Let Γ be a graph with e edges, xi vertices of degree i, and y 4-cycles. By lemma 2.4 we known that cospectral graphs have the same number of edges and closed 4-walks, respectively. Since Γ is cospectral to an H-shape tree, hence by (4) we have
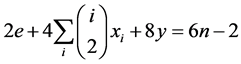
namely
 (5)
(5)
Since
 (6)
(6)
from (5), we have
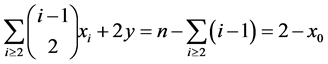 (7)
(7)
the (7) imply to y = 1 or 0.
Case 1. y = 1. by (7) we get x0 = 0 and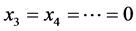 , by (5) we get
, by (5) we get 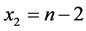 and x1 = 2, then
and x1 = 2, then .
.
We known that “the spectrum of graph Wn is the union of the spectra of the circuit C4 and the path Pn−4” [1] , that is

Case 2. y = 0. By (7) we have x0 ≤ 2.
If x0 = 0, then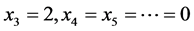 , by (5) we get
, by (5) we get 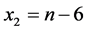 and x1= 4. Thus Γ have the same degree sequences as the H-shape tree.
and x1= 4. Thus Γ have the same degree sequences as the H-shape tree.
If x0 = 1, then  and x1 = 1. The degree sequences of Γ is
and x1 = 1. The degree sequences of Γ is .
.
If x0 = 2, then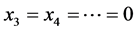 , x2 = n,
, x2 = n, 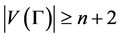 , a contradiction.
, a contradiction.
Lemma 3.3 Let G be a graph with e edges, xi vertices of degree i, and z 6-cycles. Then
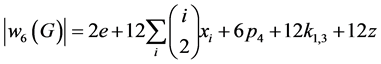 (8)
(8)
where p4 is the number of induced paths of length three and k1,3 is the number of induced star K1,3.
Proof. A close walk of length 6 can be produced from in the following five classes graphs, they are P2, P3, P4, K1,3 and C6. For an edge and a 6-cycle, it is easy to see that the number of close 6-walks equals 2 and 12, respectively. For a P3, the number of close 6-walks of a 1-degree vertex is 3 and the number of close 6-walks of the 2-degree vertex is 6, since the number of induced paths of length two is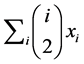 , hence for all induced paths P3, the number of close 6-walks is
, hence for all induced paths P3, the number of close 6-walks is . For a P4, since the number of close 6-walks of a 1-degree vertex is 1 and the number of close 6-walks of a 2-degree vertex is 2, hence for all induced paths P4, the number of close 6-walks is 6p4. Similarly, for a K1,3, the number of close 6-walks of a 1-degree vertex is 2 and the number of close 6-walks of the 3-degree vertex is 6, thus for all induced stars K1,3, the number of close 6-walks is 12k1,3.
. For a P4, since the number of close 6-walks of a 1-degree vertex is 1 and the number of close 6-walks of a 2-degree vertex is 2, hence for all induced paths P4, the number of close 6-walks is 6p4. Similarly, for a K1,3, the number of close 6-walks of a 1-degree vertex is 2 and the number of close 6-walks of the 3-degree vertex is 6, thus for all induced stars K1,3, the number of close 6-walks is 12k1,3.
Corollary 3.4 Let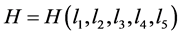 , then
, then
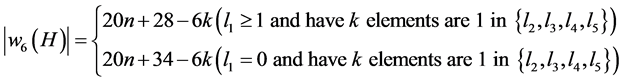 (9)
(9)
where .
.
Proof. Case 1. l1 ≥1.
1) If k = 0, that is , then
, then

where  and
and  are the number of induced paths P4 in
are the number of induced paths P4 in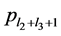 .
.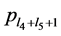 and
and , respectively. The 8(= 4 + 4) is the number of induced paths of through a 3-degree vertex u (or v). If P4 is such a induced path, then u is an internal vertex in the P4 and have at least a vertex in the
, respectively. The 8(= 4 + 4) is the number of induced paths of through a 3-degree vertex u (or v). If P4 is such a induced path, then u is an internal vertex in the P4 and have at least a vertex in the (or
(or ).
).
2) If k ≠ 0, then
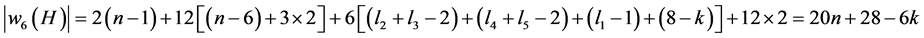
Case 2. l1 = 0.
1) If k ≠ 0, then

2) If k = 0, similarly, we have .
.
Example 1. Let , by (9) we have
, by (9) we have
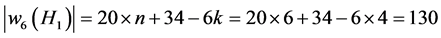 if we give to a suitable label for the H1, by a simple calculation we can get the diagonal matrix of
if we give to a suitable label for the H1, by a simple calculation we can get the diagonal matrix of , that is
, that is

clearly, the sum of the elements in the diagonal matrix equals 4 × 11 + 2 × 43 = 130.
Example 2. Let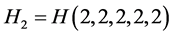 , by (9) we have
, by (9) we have , similarly, if we give to a suitable label for the H2, then we can get the diagonal matrix of
, similarly, if we give to a suitable label for the H2, then we can get the diagonal matrix of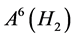 , that is
, that is

clearly, the sum of the elements in the diagonal matrix equals 4 × 6 + 4 × 22 + 2 × 29 + 2 × 49 = 268.
Lemma 3.5 Let Γ be a graph with n vertices, e edges, xi vertices of degree i, and z 6-cycles. If Γ cospectral to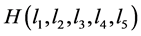 and Γ ≠ Wn, then
and Γ ≠ Wn, then
 (10)
(10)
where 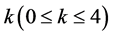 is the number of elements of equals 1 in
is the number of elements of equals 1 in 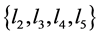 and p4 is the number of induced paths of length three and k1,3 is the number of induced star K1,3 in Γ.
and p4 is the number of induced paths of length three and k1,3 is the number of induced star K1,3 in Γ.
Proof. If l1 ≥ 1, by Lemma 3.3 we have

Similarly, when l1 = 0 the (10) hold.
Definition 1. Let U be a graph obtained from a cycle Cg (g is even and 6 ≤ g ≤ n1 − 2) and a path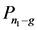 , such that identifying an end vertex in the path and any one vertex in the cycle, and uniting an isolated vertex K1.
, such that identifying an end vertex in the path and any one vertex in the cycle, and uniting an isolated vertex K1.
If a graph have the degree sequences , then the graph is U uniting some cycle.
, then the graph is U uniting some cycle.
Lemma 3.6 Let U′ be a graph with degree sequences . If U′ cospectral to an H-shape, then U′ and H satisfying one of the following conditions.
. If U′ cospectral to an H-shape, then U′ and H satisfying one of the following conditions.
1) There are one 6-cycle in U′ and l1 ≥ 1, l2, l3, l4, l5 ≥ 2.
2) There are one 6-cycle in U′ and l1 = 0, have an element is 1 in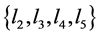 .
.
3) No 6-cycle in U′ and l1 ≥ 1, have two elements are 1 in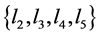 .
.
4) No 6-cycle in U′ and l1 = 0, have three elements are 1 in .
.
Proof. Without loss of generality, Let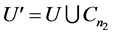 , where
, where 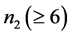 is even and n1 + n2 = n. Let U′ have e edges, xi vertices of degree i, and z 6-cycles.
is even and n1 + n2 = n. Let U′ have e edges, xi vertices of degree i, and z 6-cycles.
Case 1. l1 ≥ 1. By Lemma 3.5 we have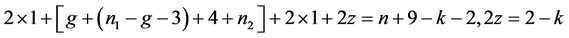 , get k = 0, z = 1 or k = 2, z = 0.
, get k = 0, z = 1 or k = 2, z = 0.
Case 2. l1 = 0, we have , get k = 1, z = 1 or k = 3, z = 0.
, get k = 1, z = 1 or k = 3, z = 0.
Lemma 3.7 Let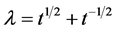 , then
, then
 (11)
(11)
Proof. By Lemma 2.1 (b) and Lemma 2.2 we have
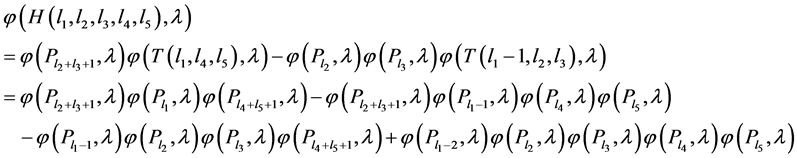 (12)
(12)

If a graph has the same degree sequences as the H-shape, then Γ is one of the following graphs G1, G2, G3, G4, G5 in figure or it is an H-shape.
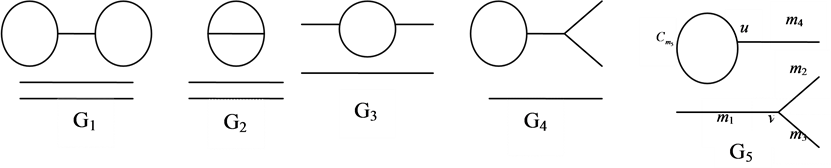
Lemma 3.8 If Γ is cospectral to an H-shape tree, then Γ contains no 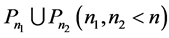 as two connected component.
as two connected component.
Proof. Assume that Γ contains a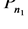 as a connected component, by (11) some li is equal, without loss of generality, let l1 = l2 = l4 = n1, then
as a connected component, by (11) some li is equal, without loss of generality, let l1 = l2 = l4 = n1, then
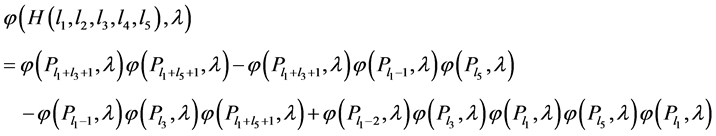
If Γ contains a 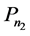 as a connected component, then l3 = l5 and l1 + l3 + 1 = l1, a contradiction.
as a connected component, then l3 = l5 and l1 + l3 + 1 = l1, a contradiction.
Thus, if a graph  cospectral to an H-shape and have the same degree sequences as the H-shape, then Γ is one of the following graphs G3, G4, G5 (Fig.) uniting some even cycle, respectively, or it is an H-shape.
cospectral to an H-shape and have the same degree sequences as the H-shape, then Γ is one of the following graphs G3, G4, G5 (Fig.) uniting some even cycle, respectively, or it is an H-shape.
Lemma 3.9 If  and
and  are cospectral, then
are cospectral, then 
Proof. By (11) we have
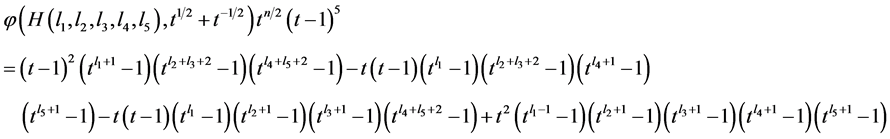 (13)
(13)
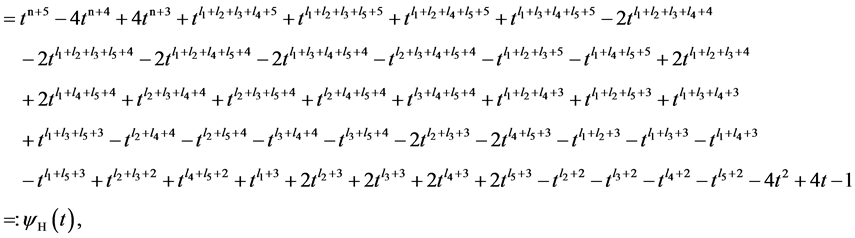 (14)
(14)
where . By (14) we have
. By (14) we have

Let , without loss of generality, we assume that l2 ≥ l3 ≥ l4 ≥ l5 and m2 ≥ m3 ≥ m4 ≥ m5. Comparing the 4th lowest term of
, without loss of generality, we assume that l2 ≥ l3 ≥ l4 ≥ l5 and m2 ≥ m3 ≥ m4 ≥ m5. Comparing the 4th lowest term of 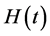 and
and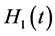 , we get m5 = l5. Similarly, we comparing the 5th, 6th and 7th lowest term of
, we get m5 = l5. Similarly, we comparing the 5th, 6th and 7th lowest term of 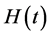 and
and , respectively, we get m4 = l4, m3 = l3 and m2 = l2. By
, respectively, we get m4 = l4, m3 = l3 and m2 = l2. By  , we get m1 = l1, thus
, we get m1 = l1, thus 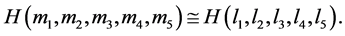
Lemma 3.10 Let G5 be a graph in Figure, then G5 and H-shape are not cospectral.
Proof. Let 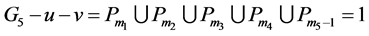
 , that is
, that is  . Denote the first component by G5,1 and the second component by G5,2. By Lemma 2.1 and Lemma 2.3 we have
. Denote the first component by G5,1 and the second component by G5,2. By Lemma 2.1 and Lemma 2.3 we have
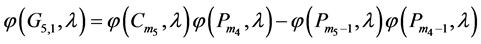
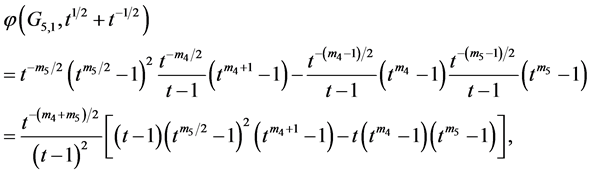


By Lemma 2.1 (a) we have
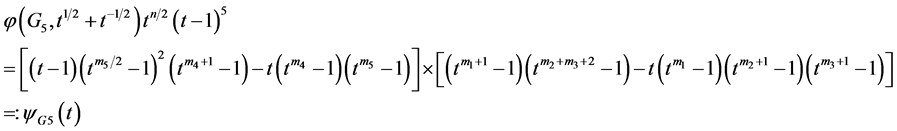 (15)
(15)
Comparing (14) and (15), since  for any
for any  and
and 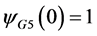 for any
for any  , hence
, hence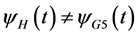 . G5 and H-shape are not cospectral.
. G5 and H-shape are not cospectral.
Remark. If G5 uniting some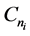 , without loss of generality, let
, without loss of generality, let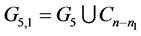 , where m1 + m2 + m3 + m4 + m5 + 1 = n1. Since
, where m1 + m2 + m3 + m4 + m5 + 1 = n1. Since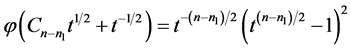 , we have
, we have 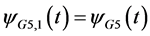
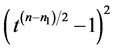 ,
, 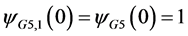 ,
, . Thus, G5,1 and H-shape are not cospectral.
. Thus, G5,1 and H-shape are not cospectral.
Theorem 3.11 Let 
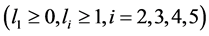 , if a graph Γ (Γ ≠ Wn) cospectral to an H-shape, then either Γ is U (Definition 1) uniting some even cycles
, if a graph Γ (Γ ≠ Wn) cospectral to an H-shape, then either Γ is U (Definition 1) uniting some even cycles  (ni ≥ 6), denoted by U′, and U′, H satisfying one of the following conditions.
(ni ≥ 6), denoted by U′, and U′, H satisfying one of the following conditions.
1) There are one 6-cycle in U′ and l1 ≥ 1, l2, l3, l4, l5 ≥ 2.
2) There are one 6-cycle in U′ and l1 = 0, have 1 element is 1 in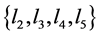 .
.
3) No 6-cycle in U′ and l1 ≥ 1, have 2 elements are 1 in .
.
4) No 6-cycle in U′ and l1 = 0, have 3 elements are 1 in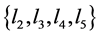 , or Γ is the graph G3 and G4 in Figure uniting some even cycles
, or Γ is the graph G3 and G4 in Figure uniting some even cycles , respectively.
, respectively.
Proof. This result is contained from Lemma 3.2 up to Lemma 3.10.
Funding
This work is supported by the Natural Science Foundation of Qinghai Province (Grant No. 2011-Z-911).
References
- Cvetkovi'c, D., Doob, M. and Sachs, H. (1980) Spectra of Graphs—Theory and Application. Academic Press, New York.
- van Dam, E.R. and Haemers, W.H. (2003) Which Graph Are Determined by Their Spectrum? Linear Algebra and Its Applications, 373, 241-272. http://dx.doi.org/10.1016/S0024-3795(03)00483-X
- Doob, M. and Haemers, W.H. (2002) The Complement of the Path Is Determined by Its Spectrum. Linear Algebra and Its Applications, 356, 57-65. http://dx.doi.org/10.1016/S0024-3795(02)00323-3
- Noy, M. (2003) Graphs Determined by Polynomial Invariants. Theoretical Computer Science, 307, 365-384.
- Smith, J.H. (1970) Some Propertice of the Spectrum of Graph. In: Guy, R., et al., Eds., Combinatorial Structure and Their Applications, Gordon and Breach, New York, 403-406.
- Wang, W. and Xu, C.-X. (2006) On the Spactral Characterization of T-Shape Trees. Linear Algebra and Its Applications, 414, 492-501.http://dx.doi.org/10.1016/j.laa.2005.10.031
- Schwenk, A.J. (1973) Almost All Trees Are Cospectral. In: Harary, F., Ed., New Directions in the Theory of Graphs, Academic Press, New York, 275-307.
- Godsil, C.D. (1993) Algebraic Combinatorics. Chapman & Hall, New York.
- Sachs, H. (1964) Beziehungen zwischen den in einem graphen enthaltenen kreisenund seinem charakteristischen polynom. Publicationes Mathematicae, 11, 119-134.
- Omidi, G.R. and Tajbakhsh, K. (2007) Starlike Trees Are Determined by Their Laplacian Spectrum. Linear Algebra and Its Applications, 422, 654-658. http://dx.doi.org/10.1016/j.laa.2006.11.028

