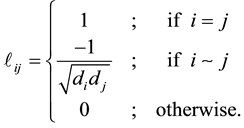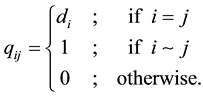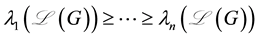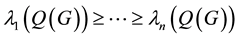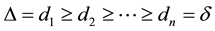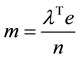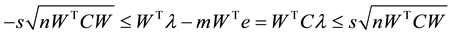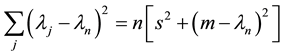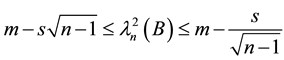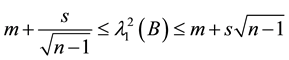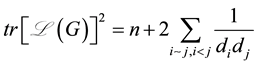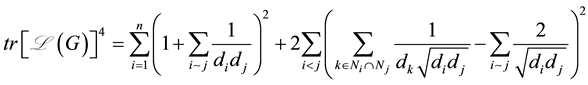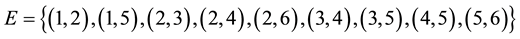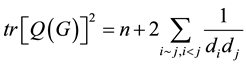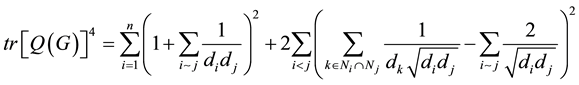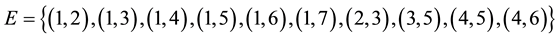Advances in Linear Algebra & Matrix Theory
Vol.04 No.04(2014), Article ID:51423,3 pages
10.4236/alamt.2014.44017
The Bounds for Eigenvalues of Normalized Laplacian Matrices and Signless Laplacian Matrices
Serife Büyükköse1, Sehri Gülçiçek Eski2
1Department of Mathematics, Faculty of Science, Gazi University, Ankara, Turkey
2Institue of Science, Ahi Evran University, Kırşehir, Turkey
Email: serifebuyukkose@gmail.com, gulcicekeski@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 September 2014; revised 6 October 2014; accepted 5 November 2014
ABSTRACT
In this paper, we found the bounds of the extreme eigenvalues of normalized Laplacian matrices and signless Laplacian matrices by using their traces. In addition, we found the bounds for k-th eigenvalues of normalized Laplacian matrix and signless Laplacian matrix.
Keywords:
Normalized Laplacian Matrix, Signless Laplacian Matrix, Bounds of Eigenvalue

1. Introduction
Let
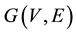 be a simple graph with the vertex set
be a simple graph with the vertex set
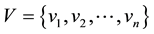 and edge set of E. For
and edge set of E. For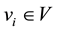 , the degree of
, the degree of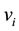 , the set of neighbours of
, the set of neighbours of
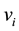 are denoted by
are denoted by
 and
and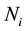 , respectively. If
, respectively. If
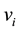 and
and
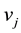 are adjacent, we denote
are adjacent, we denote
 of short use
of short use .
.
The adjacency matrix, Laplacian matrix and diagonal matrix of vertex degree of a
 graph are denoted by
graph are denoted by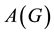 ,
,
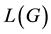 ,
,
 , respectively. Clearly
, respectively. Clearly
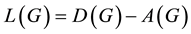
The normalized Laplacian matrix of G is defined as
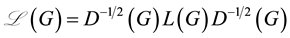

The signless Laplacian matrix of G is defined as
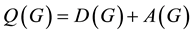
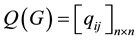
Since
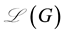

and
respectively.
Now we give some bounds for normalized Laplacian matrix and signless Laplacian matrix.
1. Oliveira and de Lima’s bound [1] : For a simple connected graph G with n vertices and m edges,
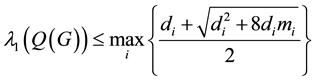
where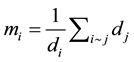
2. Another Oliveira and de Lima’s bound [1] :
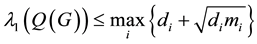
where
3. Li, Liu et al. bound’s [2] [3] :

4. Rojo and Soto’s bound [4] : If
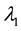
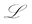

where the minimum is taken over all pairs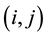
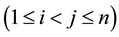
In this paper, we found extreme eigenvalues of normalized Laplacian matrix and signless Laplacian matrix of a G graph with using theirs traces.
To obtain bounds for eigenvalues of
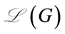

Lemma 1. Let W and

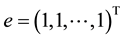
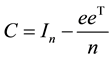
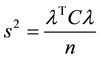
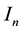
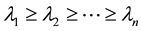
Theorem 1 [5] . Let A be a
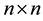
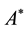
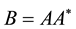
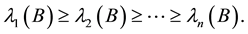
and
where
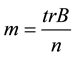
2. Main Results for Normalized Laplacian Matrix
Theorem 2. Let G be a simple graph and
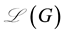
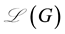
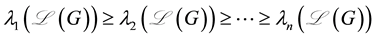
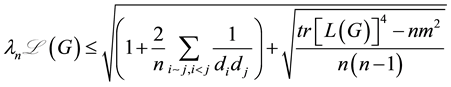
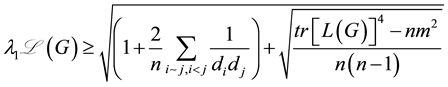
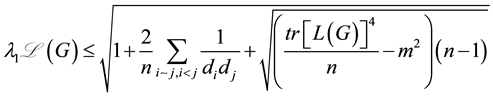
Proof. Clearly
and
Since
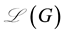
Example 1. Let
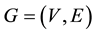
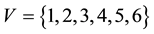
3. Main Results for Signless Laplacian Matrix
Theorem 3. Let G be a simple graph and
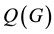

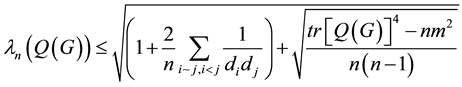
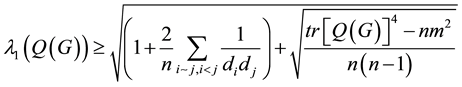
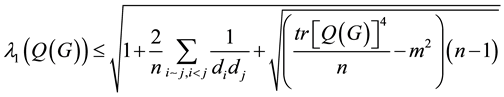
Proof. Clearly
and
Since
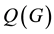
Example 2. Let
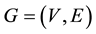
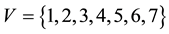
Cite this paper
SerifeBüyükköse,Sehri GülçiçekEski, (2014) The Bounds for Eigenvalues of Normalized Laplacian Matrices and Signless Laplacian Matrices. Advances in Linear Algebra & Matrix Theory,04,201-204. doi: 10.4236/alamt.2014.44017
References
- 1. Oliveira, C.S., De Lima, L.S., De Abreu, N.M.M. and Hansen, P. (2010) Bound on the Index of the Signless Laplacian of a Graph. Discrete Applied Mathematics, 158, 355-360.
http://dx.doi.org/10.1016/j.dam.2009.06.023 - 2. Li, J. and Pan, Y. (2004) Upper Bounds for the Laplacian Graph Eigenvalues. Acta Mathematica Sinica, English Series, 20, 803-806.
http://dx.doi.org/10.1007/s10114-004-0332-4 - 3. Liu, H., Lu, M. and Tian, F. (2004) On the Laplacian Spectral Radius of a Graph. Linear Algebra and Its Applications, 376, 135-141.
http://dx.doi.org/10.1016/j.laa.2003.06.007 - 4. Rojo, O. and Soto, R.L. (2013) A New Upper Bound on the Largest Normalized Laplacian Eigenvals. Operators and Matrices, 7, 323-332.
http://dx.doi.org/10.7153/oam-07-19 - 5. Wolkowich, H. and Styan, G.P.H. (1980) Bounds for Eigenvalues Using Traces of Matrice. Linear Algebra and Its Applications, 29, 471-506.
http://dx.doi.org/10.1016/0024-3795(80)90258-X