Advances in Linear Algebra & Matrix Theory
Vol.2 No.3(2012), Article ID:22664,7 pages DOI:10.4236/alamt.2012.23005
A Modified Precondition in the Gauss-Seidel Method
Department of Mathematics, Faculty of Science, Arak University, Arak, Iran
Email: a-nazari@araku.ac.ir, z-borujeni@arshad.araku.ac.ir
Received March 6, 2012; revised June 28, 2012; accepted August 21, 2012
Keywords: Preconditioning; Gauss-Seidel Method; Regular Splitting; Z-Matrix; Nonnegative Matrix
ABSTRACT
In recent years, a number of preconditioners have been applied to solve the linear systems with Gauss-Seidel method (see [1-13]). In this paper we use Sl instead of (S + Sm) and compare with M. Morimoto’s precondition [3] and H. Niki’s precondition [5] to obtain better convergence rate. A numerical example is given which shows the preference of our method.
1. Introduction
Consider the linear system
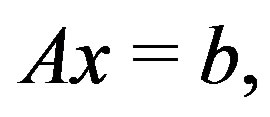 (1)
(1)
where 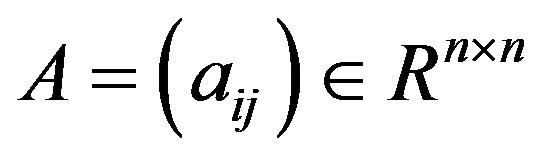 is a known nonsingular matrix and
is a known nonsingular matrix and 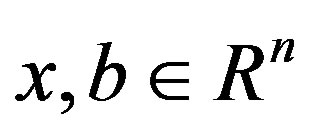 are vectors. For any splitting A = M – N with a nonsingular matrix M, the basic splitting iterative method can be expressed as
are vectors. For any splitting A = M – N with a nonsingular matrix M, the basic splitting iterative method can be expressed as
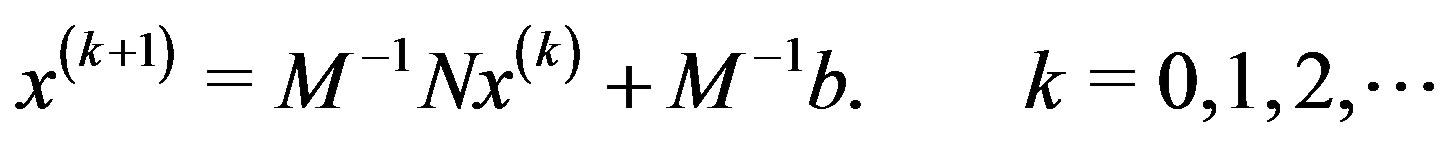 (2)
(2)
Assume that
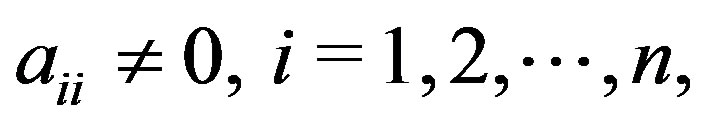
without loss of generality we can write
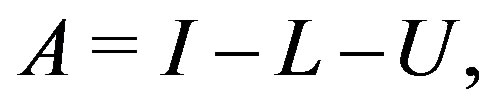 (3)
(3)
where I is the identity matrix,  and
and  are strictly lower triangular and strictly upper triangular parts of
are strictly lower triangular and strictly upper triangular parts of , respectively. In order to accelerate the convergence of the iterative method for solving the linear system (1), the original linear system (1) is transformed into the following preconditioned linear system
, respectively. In order to accelerate the convergence of the iterative method for solving the linear system (1), the original linear system (1) is transformed into the following preconditioned linear system
 (4)
(4)
where P, called a preconditioner, is a nonsingular matrix.
In 1991, Gunawardena et al. [2] considered the modified Gauss-Seidel method with , where
, where
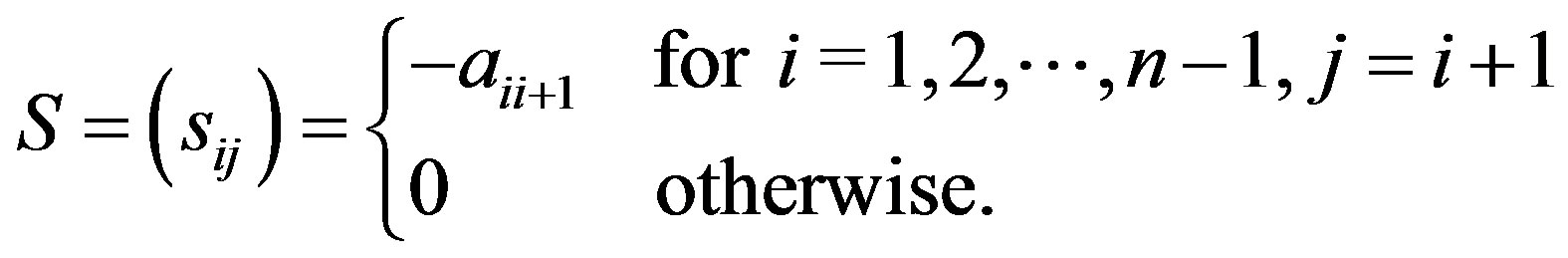
Then, the preconditioned matrix 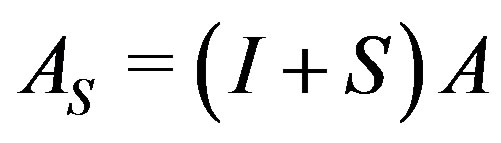 can be written as
can be written as
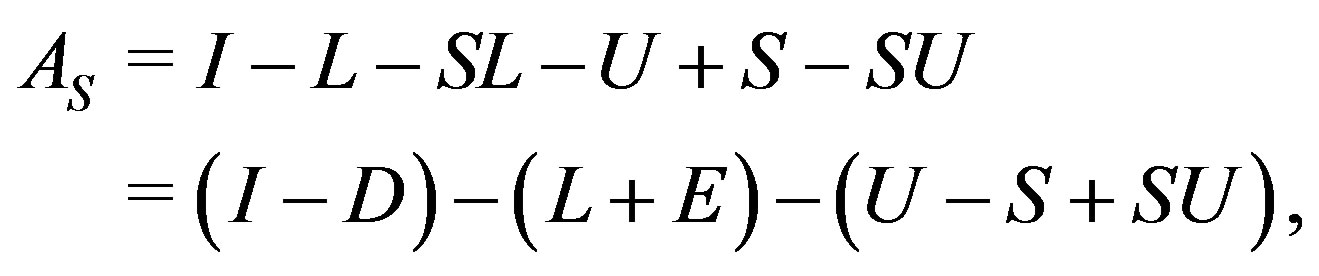
where D and E are the diagonal and strictly lower triangular parts of SL, respectively. If 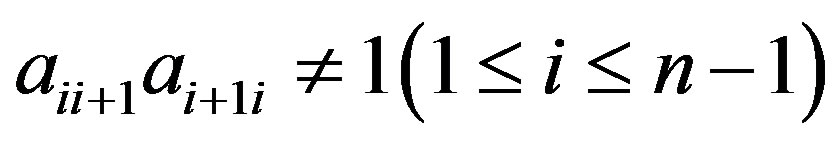 , then
, then  exists. Therefore, the preconditioned Gauss-Seidel iterative matrix
exists. Therefore, the preconditioned Gauss-Seidel iterative matrix  for
for 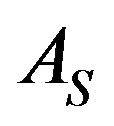 becomes
becomes

which is referred to as the modified Gauss-Seidel iterative matrix. Gunawardena et al. proved the following inequality:
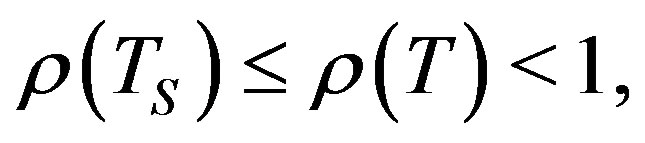
where  denotes the spectral radius of the GaussSeidel iterative matrix T. Morimoto et al. [3] have proposed the following preconditioner,
denotes the spectral radius of the GaussSeidel iterative matrix T. Morimoto et al. [3] have proposed the following preconditioner,
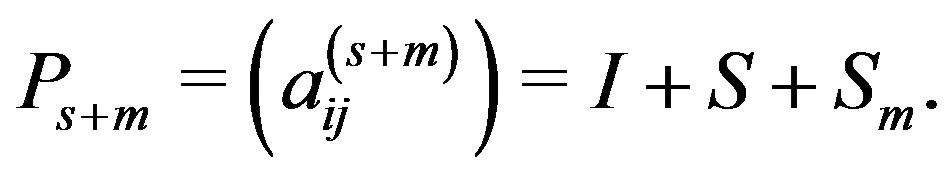
In this preconditioner,  is defined by
is defined by
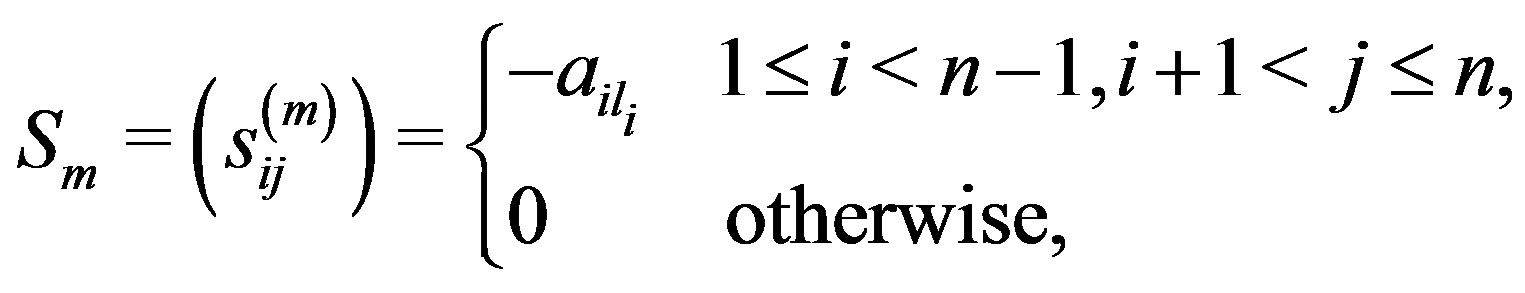
where 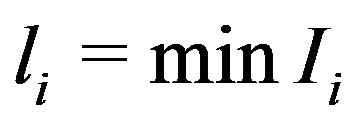 and
and
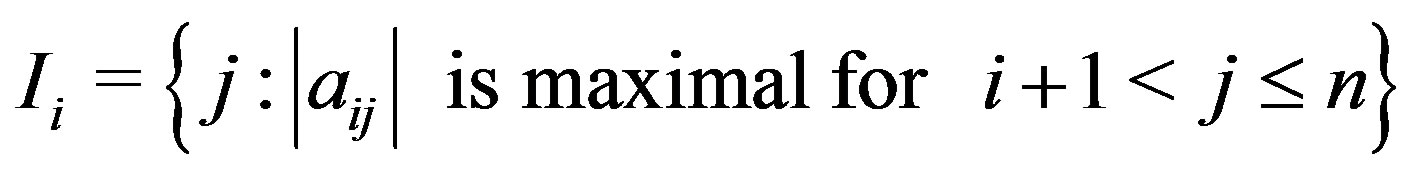 , for
, for
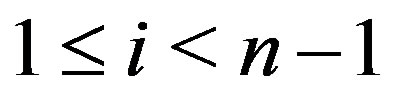 . The preconditioned matrix
. The preconditioned matrix  can then be written as
can then be written as

where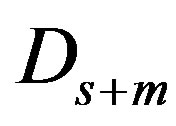 ,
, 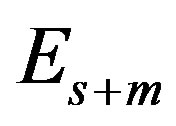 and
and 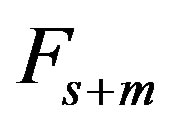 are the diagonal, strictly lower and strictly upper triangular parts of
are the diagonal, strictly lower and strictly upper triangular parts of 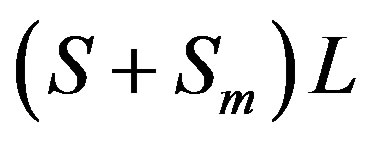 respectively. Assume that the following inequalities are satisfied:
respectively. Assume that the following inequalities are satisfied:

Then  is nonsingular. The preconditioned Gauss-Seidel iterative matrix
is nonsingular. The preconditioned Gauss-Seidel iterative matrix 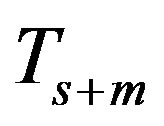 for
for 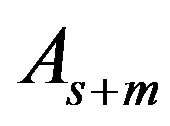 is then defined by
is then defined by
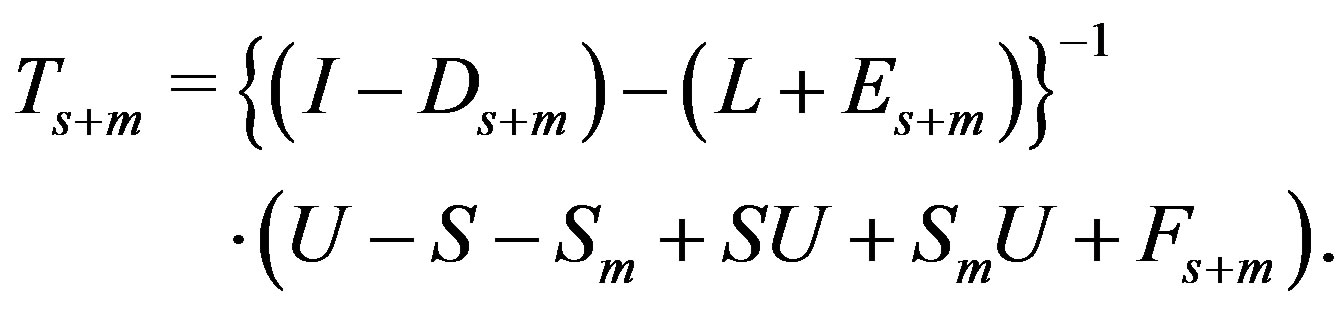
Morimoto et al. [3] proved that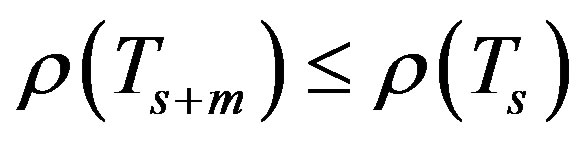 . To extend the preconditioning effect to the last row, Morimoto et al. [7] proposed the preconditioner
. To extend the preconditioning effect to the last row, Morimoto et al. [7] proposed the preconditioner
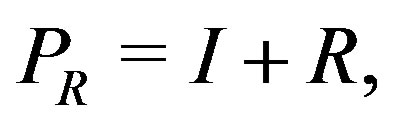
where R is defined by
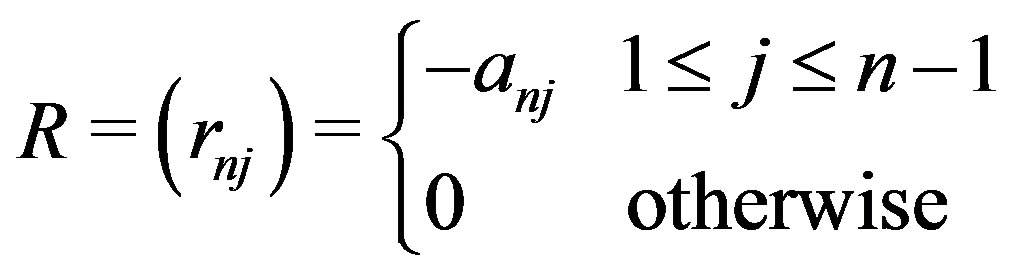
The elements 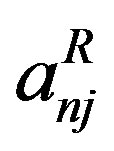 of
of  are given by
are given by
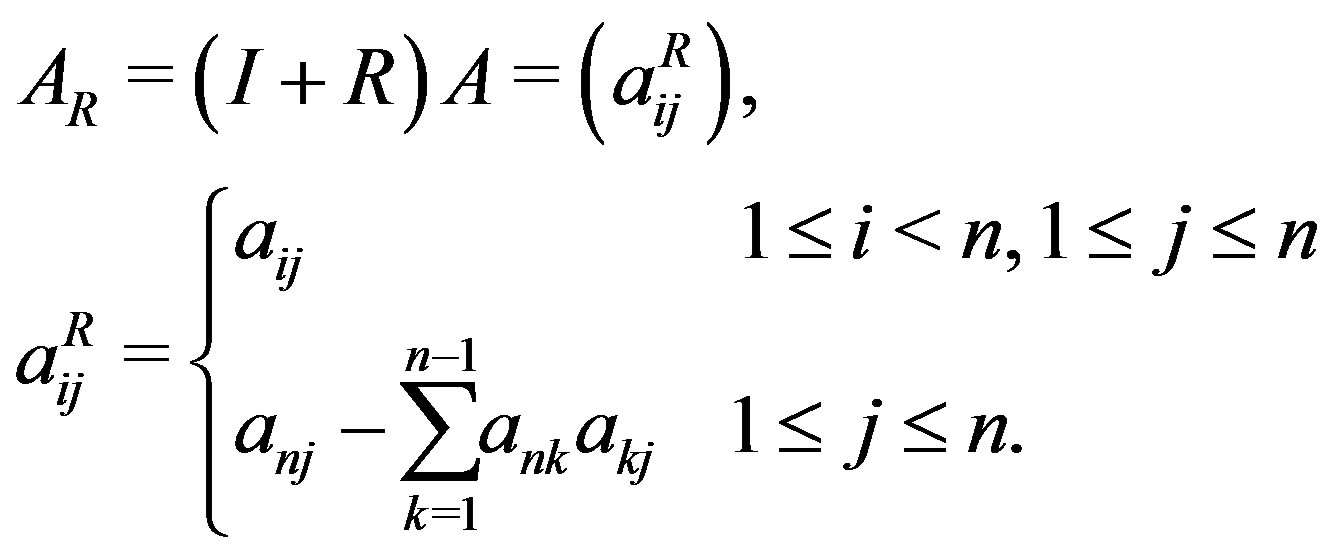
And Morimoto et al. proved that  holds, where
holds, where 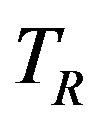 is the iterative matrix for
is the iterative matrix for . They also presented combined preconditioners, which are given by combinations of R with any upper preconditioner, and showed that the convergence rate of the combined methods are better than those of the Gauss-Seidel method applied with other upper preconditioners [7]. In [14], Niki et al. considered the preconditioner
. They also presented combined preconditioners, which are given by combinations of R with any upper preconditioner, and showed that the convergence rate of the combined methods are better than those of the Gauss-Seidel method applied with other upper preconditioners [7]. In [14], Niki et al. considered the preconditioner 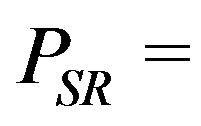
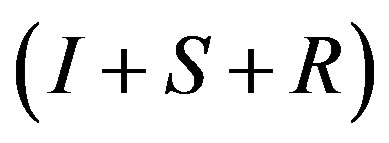 . Denote
. Denote . In [5], Niki et al. proved that if the following inequality is satisfied,
. In [5], Niki et al. proved that if the following inequality is satisfied,
 (5)
(5)
then 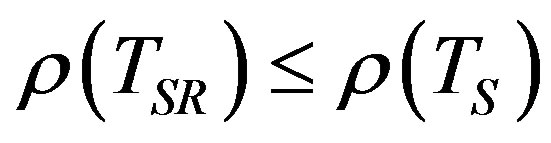 holds, where
holds, where 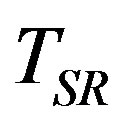 is the iterative matrix for
is the iterative matrix for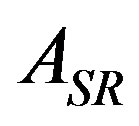 . For matrices that do not satisfy Equation
. For matrices that do not satisfy Equation
(5), by putting 
Equation (5) is satisfied. Therefore, Niki et al. [5] proposed a new preconditioner , where
, where
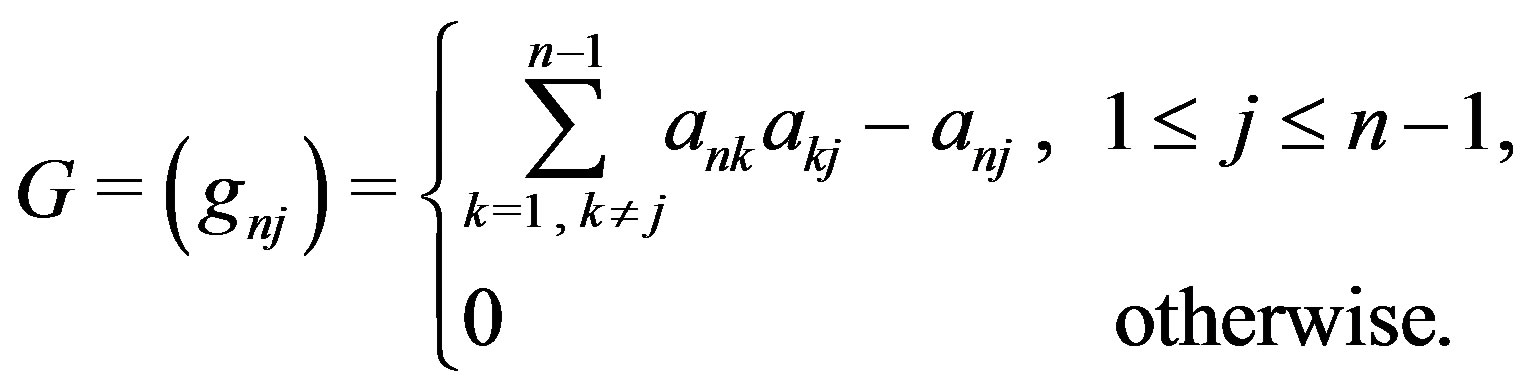
Put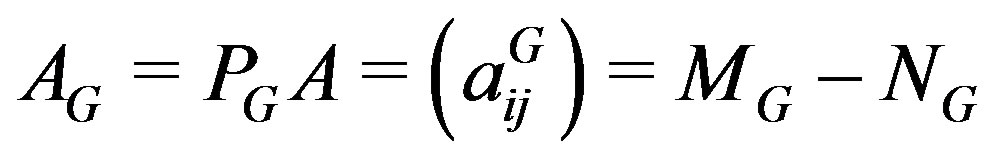 , and
, and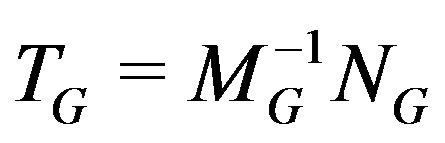 .
.
Replacing 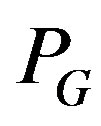 by
by 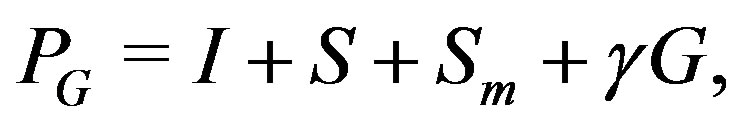 and setting
and setting  the Gauss-Seidel splitting of
the Gauss-Seidel splitting of 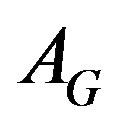 can be written as
can be written as
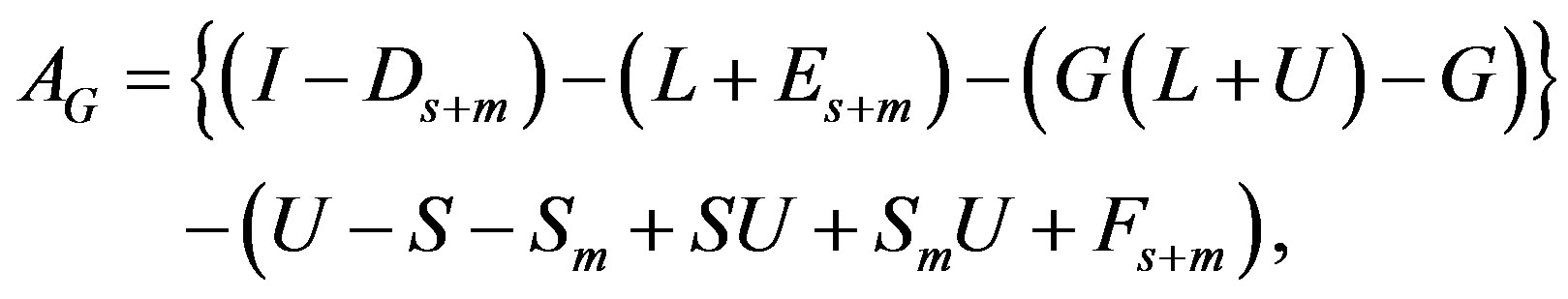
where  is constructed by the elements
is constructed by the elements . Thus, if the preconditioner
. Thus, if the preconditioner  is used, then all of the rows of
is used, then all of the rows of  are subject to preconditioning. Niki et al. [5] proved that under the condition
are subject to preconditioning. Niki et al. [5] proved that under the condition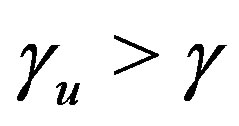 ,
,  where
where 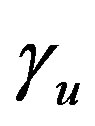 is the upper bound of those values of
is the upper bound of those values of  for which
for which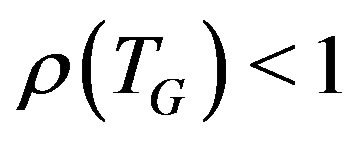 . By setting
. By setting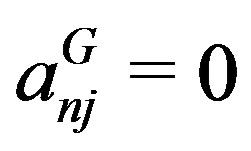 , they obtained
, they obtained
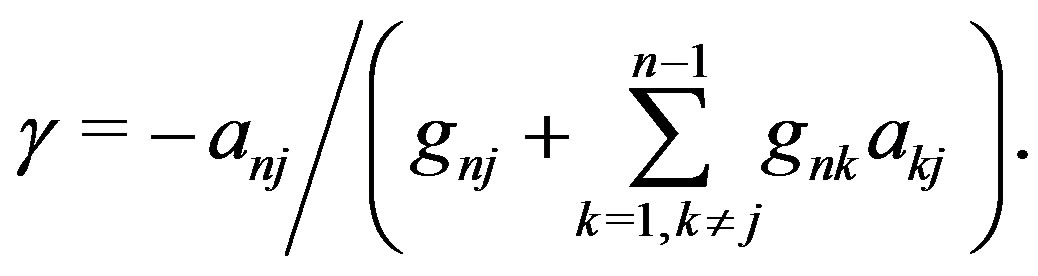
Niki et al. [5] proved that the preconditioner 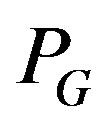 satisfies the Equation (5) unconditionally. Moreover, they reported that the convergence rate of the GaussSeidel method using preconditioner
satisfies the Equation (5) unconditionally. Moreover, they reported that the convergence rate of the GaussSeidel method using preconditioner  is better than that of the SOR method using the optimum
is better than that of the SOR method using the optimum 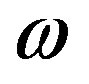 found by numerical computation. They also reported that there is an optimum
found by numerical computation. They also reported that there is an optimum  in the range
in the range 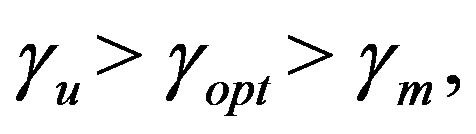 which produces an extremely small
which produces an extremely small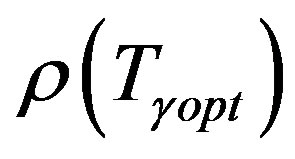 , where
, where 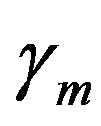 is the upper bound of the values of
is the upper bound of the values of 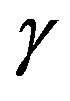 for which
for which , for all
, for all .
.
In this paper we use different preconditions for solving (1) by Gauss-Siedel method, that assuming none of the components of the matrix  to be zero. If the largest component of the column j is not
to be zero. If the largest component of the column j is not 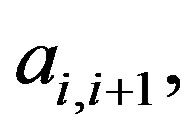 then the value of
then the value of 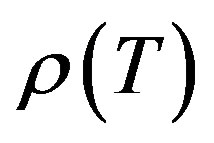 will be improved.
will be improved.
2. Main Result
In this section we replace Sl by 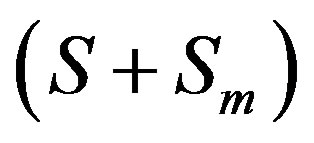 of Morimoto such that
of Morimoto such that  and define
and define  by
by

where 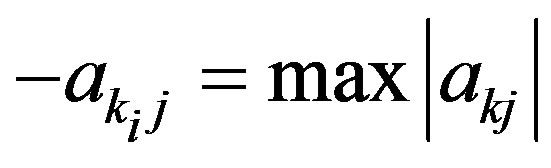 s.t
s.t , and
, and  has the same form as the
has the same form as the  proposed by Morimoto et al. [3].
proposed by Morimoto et al. [3].
The precondition Matrix 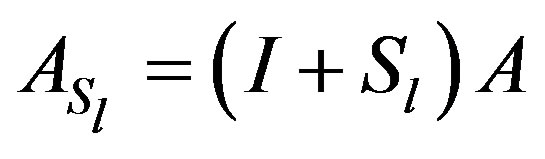 can then be written as
can then be written as
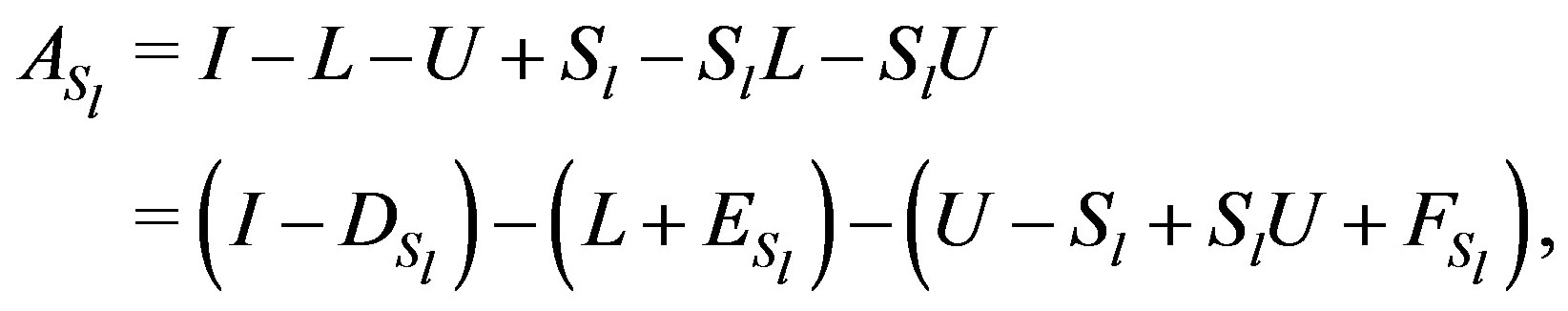
where 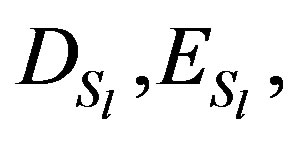 and
and 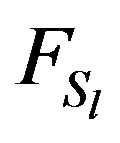 are the diagonal, strictly lower and strictly upper triangular parts of
are the diagonal, strictly lower and strictly upper triangular parts of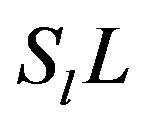 , respectively. Assume that the following inequalities are satisfied:
, respectively. Assume that the following inequalities are satisfied:
 (6)
(6)
Therefore  exists and the preconditioned GaussSeidel iterative matrix
exists and the preconditioned GaussSeidel iterative matrix 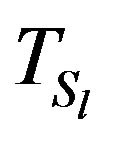 for
for  is defined by
is defined by

For 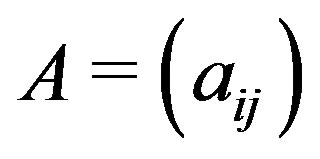 and
and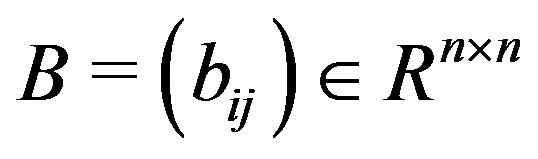 , we write
, we write 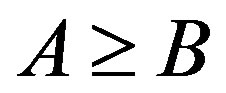 whenever
whenever 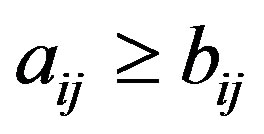 holds for all
holds for all 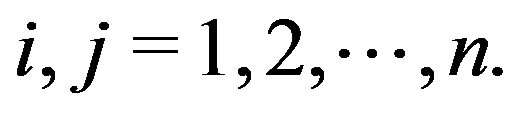 A is nonnegative if
A is nonnegative if 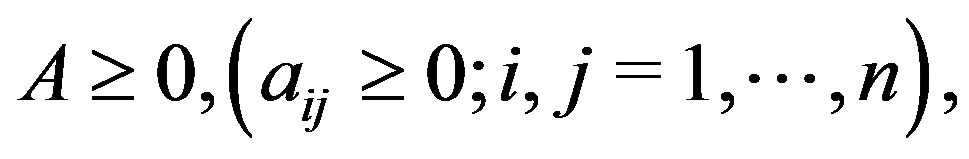 and
and 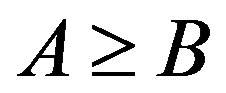 if and only if
if and only if .
.
Definition 2.1 (Young, [15]). A real 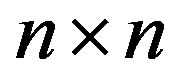 matrix
matrix  with
with  for all
for all  is called a Zmatrix.
is called a Zmatrix.
Definition 2.2 (Varga, [16]). A matrix A is irreducible if the directed graph associated to A is strongly connected.
Lemma 2.3. If A is an irreducible diagonally dominant Z-matrix with unit diagonal, and if the assumption (6) holds, then the preconditioned matrix AS is a diagonally dominant Z-matrix.
Proof. The elements  of
of  are given by
are given by
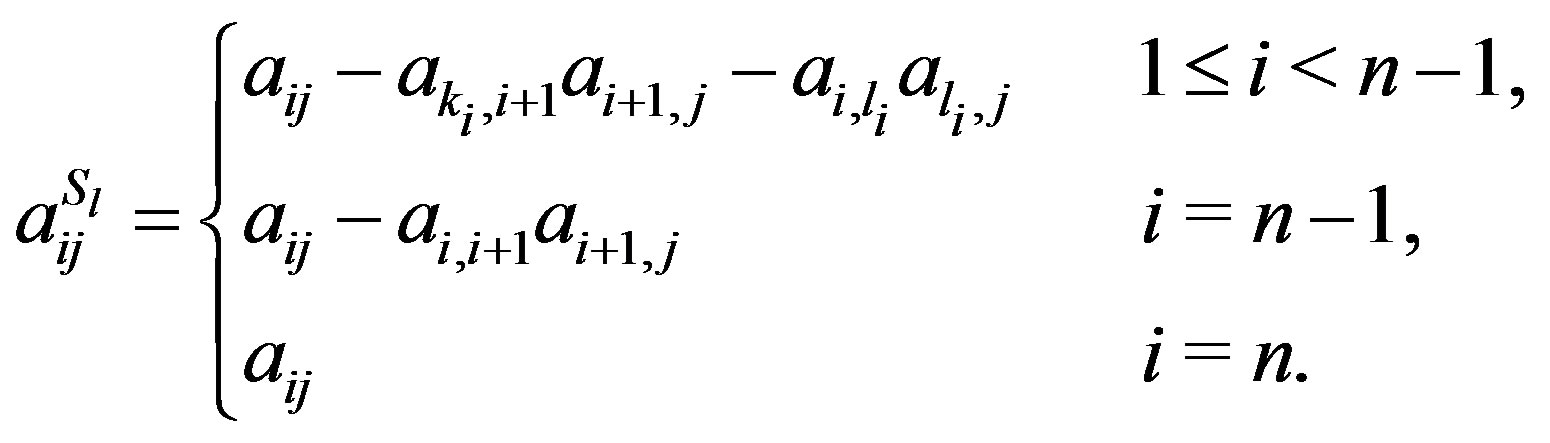 (7)
(7)
Since A is a diagonally dominant Z-matrix, so we have
 (8)
(8)
Therefore, the following inequalities hold:
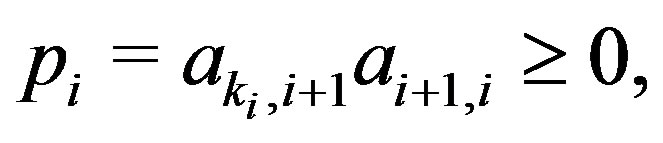




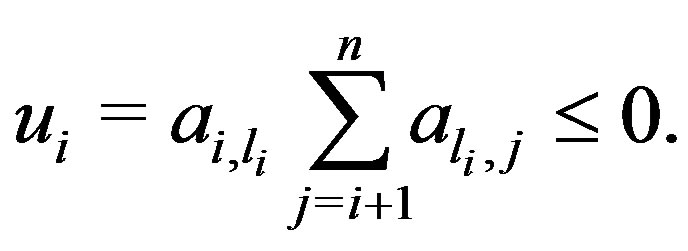
We denote that 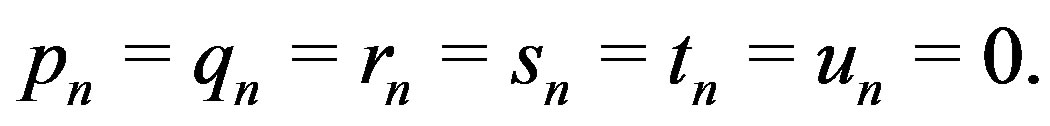 Then the following inequality holds:
Then the following inequality holds:
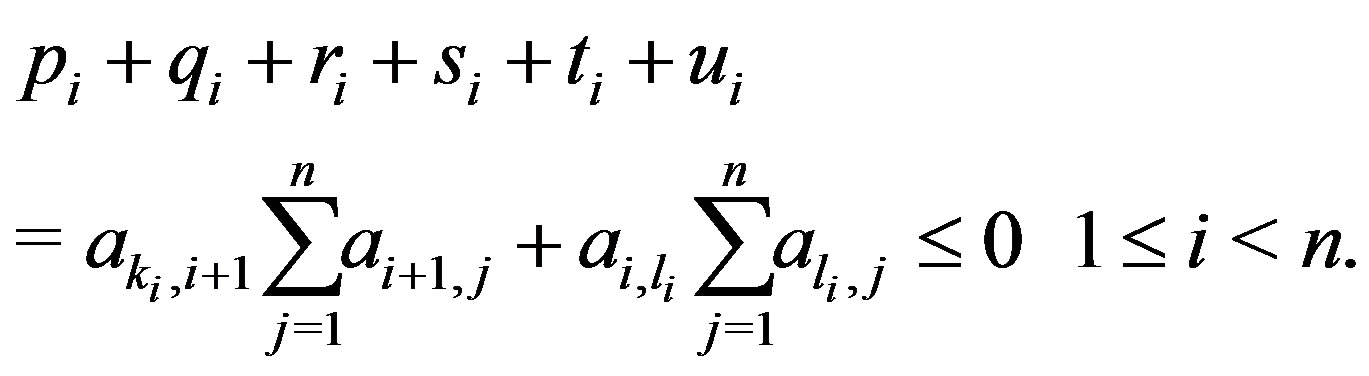
Furthermore, if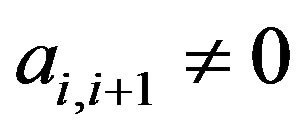 , and
, and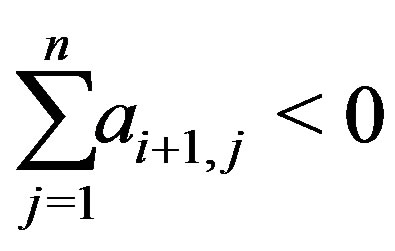 , for some
, for some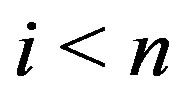 , then we have
, then we have
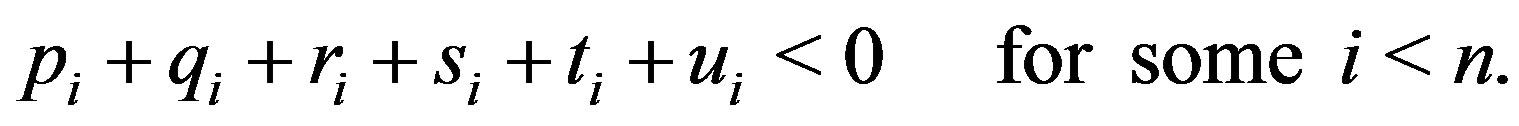 (9)
(9)
Let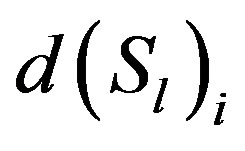 ,
, 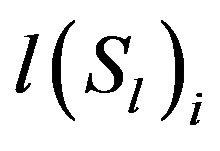 and
and 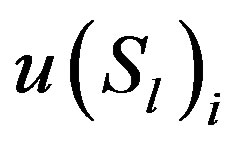 be the sums of the elements in row i of
be the sums of the elements in row i of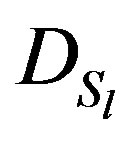 ,
, 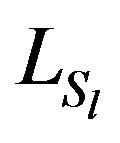 , and
, and , respectively. The following equations hold:
, respectively. The following equations hold:
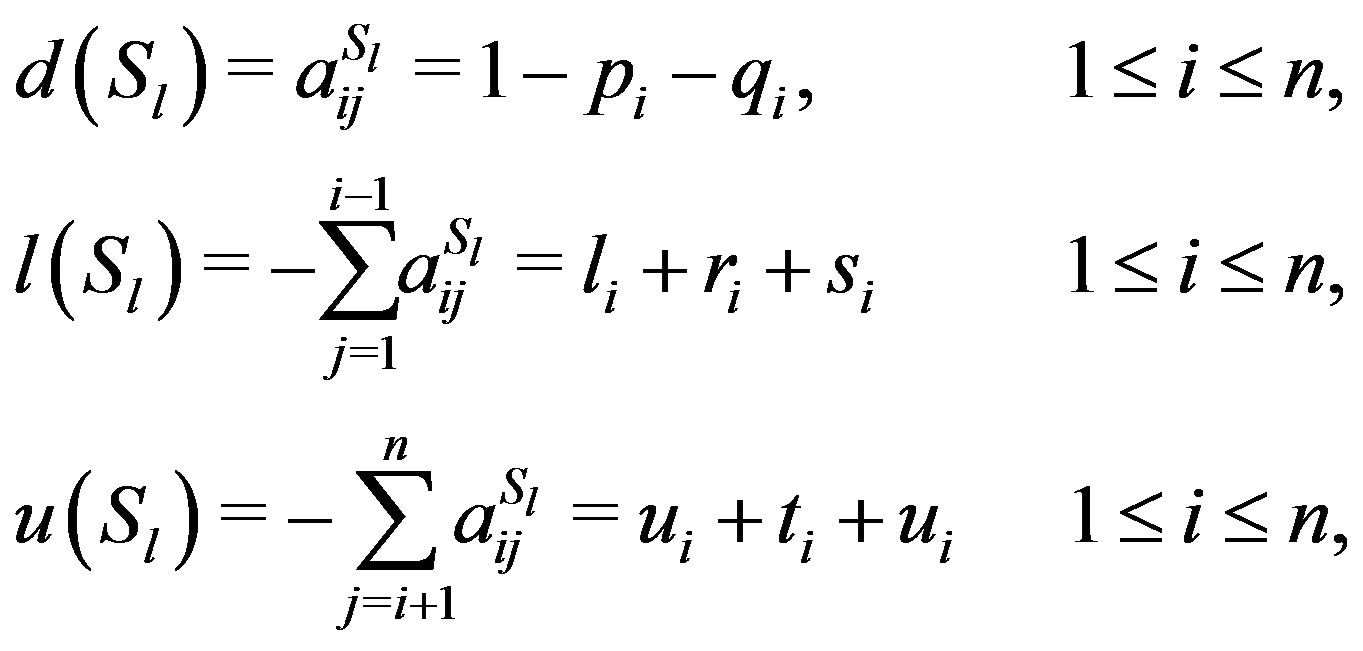 (10)
(10)
where 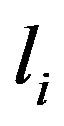 and
and  are the sums of the elements in row i of L and U for
are the sums of the elements in row i of L and U for , respectively. Since A is a diagonally dominant Z-matrix, by (8) and by the condition (6) the following relations hold:
, respectively. Since A is a diagonally dominant Z-matrix, by (8) and by the condition (6) the following relations hold:

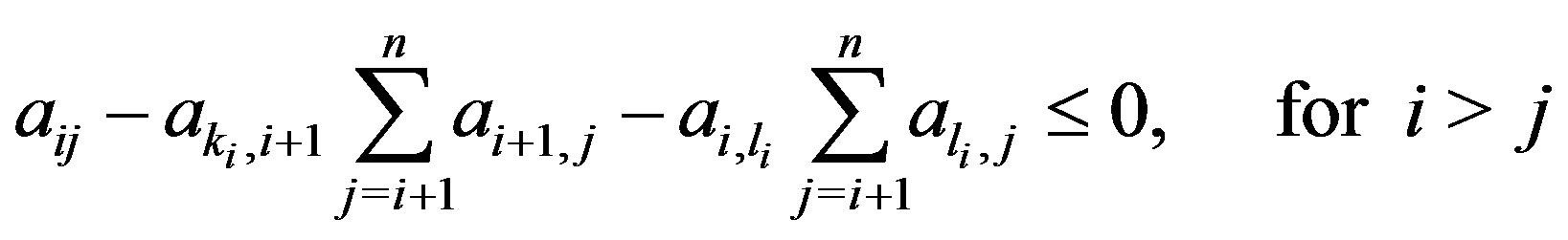

Therefore,  ,
,  , and
, and  is a Zmatrix. Moreover, by (9) and by the assumption, we can easily obtain
is a Zmatrix. Moreover, by (9) and by the assumption, we can easily obtain
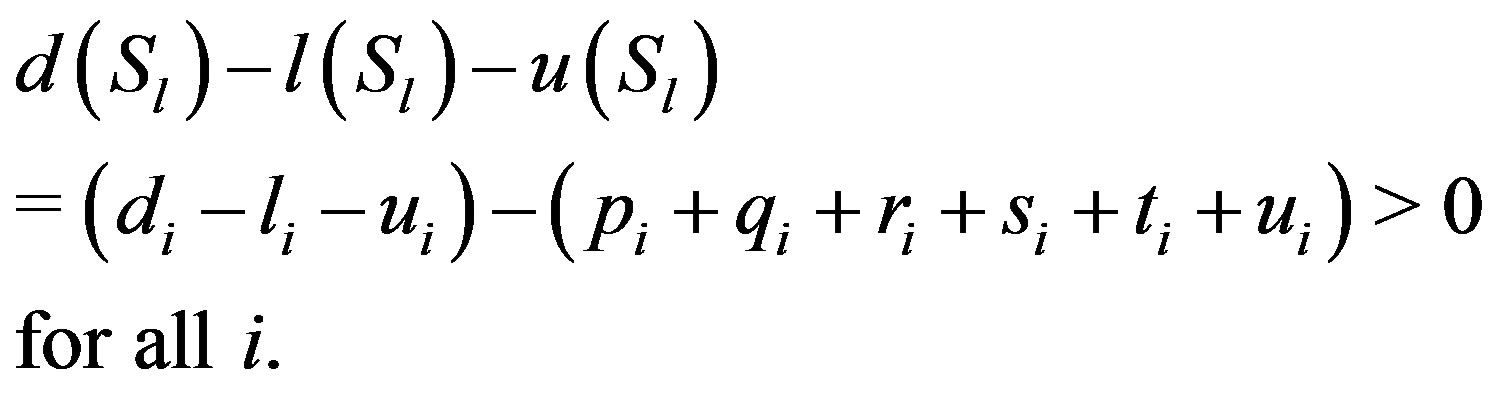 (11)
(11)
Therefore, 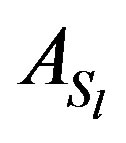 satisfies the condition of diagonal dominance.
satisfies the condition of diagonal dominance.
Lemma 2.4 [10, Lemma 2]. An upper bound on the spectral radius 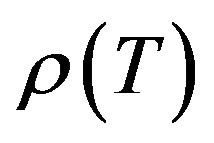 for the Gauss-Seidel iteration matrix T is given by
for the Gauss-Seidel iteration matrix T is given by
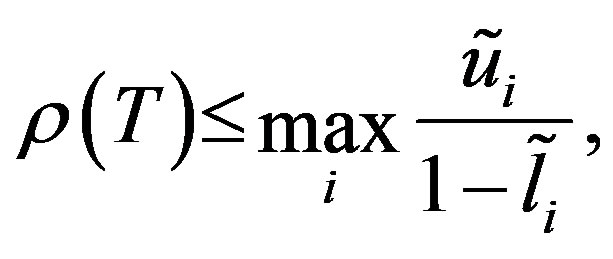
where 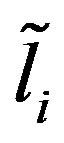 and
and 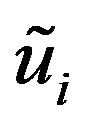 are the sums of the moduli of the elements in row i of the triangular matrices L and U, respectively.
are the sums of the moduli of the elements in row i of the triangular matrices L and U, respectively.
Theorem 2.5. Let A be a nonsingular diagonally dominant Z-matrix with unit diagonal elements and let the condition (6) holds, then 
Proof. From (11) and 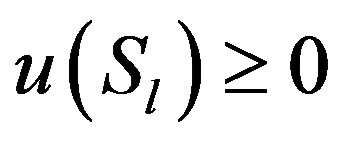 we have
we have

This implies that
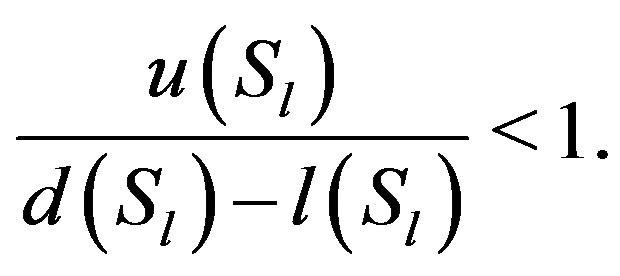 (12)
(12)
Hence, by Lemma (2.4) we have 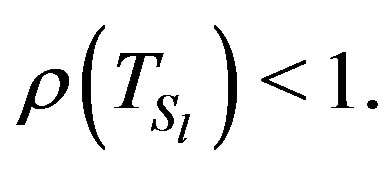
Definition 2.6. Let A be an  real matrix. Then,
real matrix. Then, 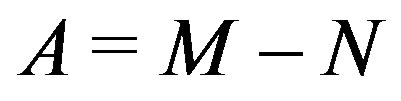 is referred to as:
is referred to as:
1) a regular splitting, if M is nonsingular, 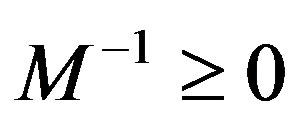 and
and 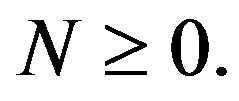
2) a weak regular splitting, if M is nonsingular, 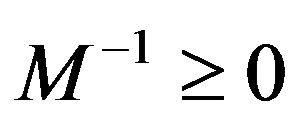 and
and 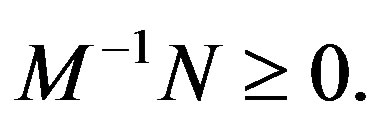
3) a convergent splitting, if 
Lemma 2.7 (Varga, [10]). Let  be a nonnegative and irreducible
be a nonnegative and irreducible 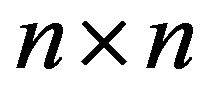 matrix. Then 1) A has a positive real eigenvalue equal to its spectral radius
matrix. Then 1) A has a positive real eigenvalue equal to its spectral radius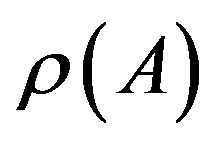 ;
;
2) for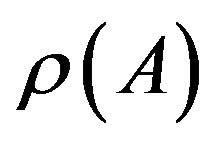 , there corresponds an eigenvector x > 0;
, there corresponds an eigenvector x > 0;
3)  is a simple eigenvalue of A;
is a simple eigenvalue of A;
4) 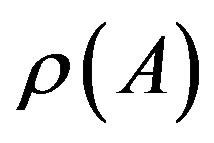 increases whenever any entry of A increases.
increases whenever any entry of A increases.
Corollary 2.8 [16, Corollary 3.20]. If  is a real, irreducibly diagonally dominant
is a real, irreducibly diagonally dominant 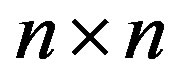 matrix with
matrix with 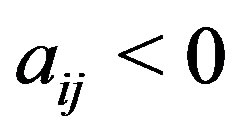 for all
for all , and
, and 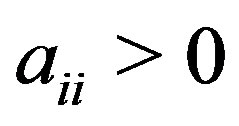 for all
for all , then
, then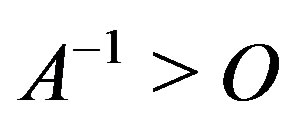 .
.
Theorem 2.9 [16, Theorem 3.29]. Let 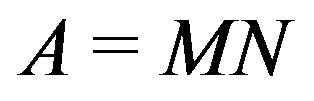 be a regular splitting of the matrix A. Then, A is nonsingular with
be a regular splitting of the matrix A. Then, A is nonsingular with 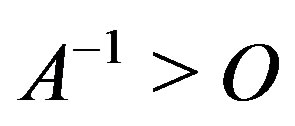 if and only if
if and only if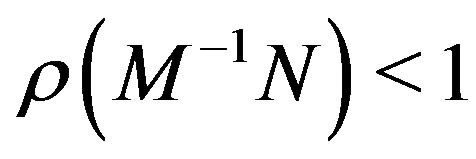 , where
, where

Theorem 2.10 (Gunawardena et al. [2, Theorem 2.2]). Let A be a nonnegative matrix. Then 1) If 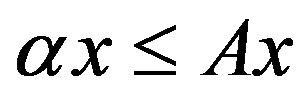 for some nonnegative vector x,
for some nonnegative vector x,  then
then 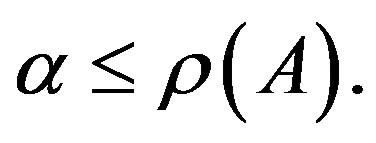
2) If 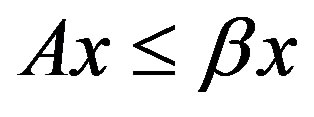 for some positive vector x, then
for some positive vector x, then 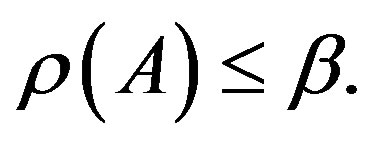 Moreover, if A is irreducible and if
Moreover, if A is irreducible and if  for some nonnegative vector x, then
for some nonnegative vector x, then 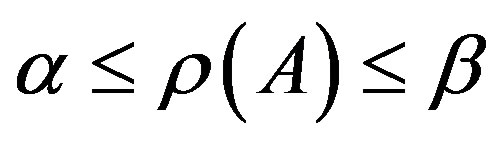 and
and  is a positive vector.
is a positive vector.
Let  be a real Banach space,
be a real Banach space,  its dual and
its dual and  the space of all bounded linear operator mapping B into itself. We assume that B is generated by a normal cone K [17]. As is defined in [17], the operator
the space of all bounded linear operator mapping B into itself. We assume that B is generated by a normal cone K [17]. As is defined in [17], the operator  has the property “d” if its dual
has the property “d” if its dual  possesses a Frobenius eigenvector in the dual cone
possesses a Frobenius eigenvector in the dual cone 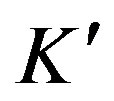 which is defined by
which is defined by

As is remarked in [1,17], when 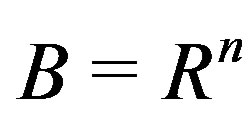 and
and , all
, all 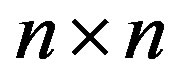 real matrices have the property “d”. Therefore the case are discussing fulfills the property “d”. For the space of all
real matrices have the property “d”. Therefore the case are discussing fulfills the property “d”. For the space of all  matrices, the theorem of Marek and Szyld can be stated as follows:
matrices, the theorem of Marek and Szyld can be stated as follows:
Theorem 2.11 (Marek and Szyld [17, Theorem 3.15]). Let 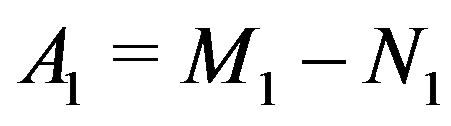 and
and  be weak regular splitting with
be weak regular splitting with . Let
. Let  be such that
be such that 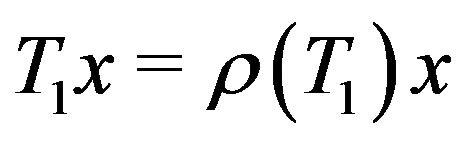 and
and . If
. If 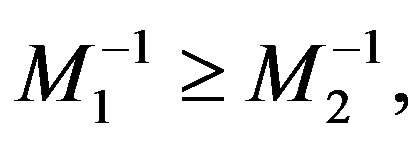 and if either
and if either 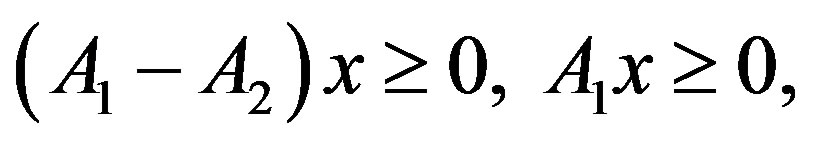 or
or 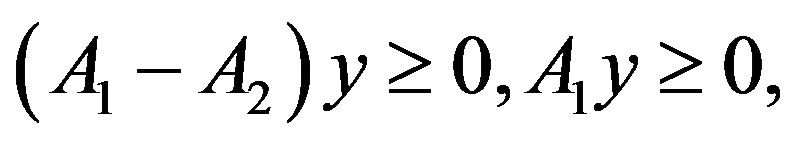 with
with , then
, then
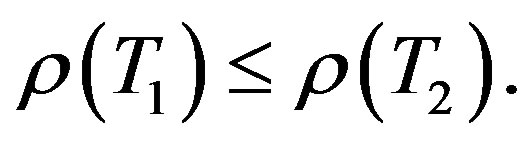
Moreover, if 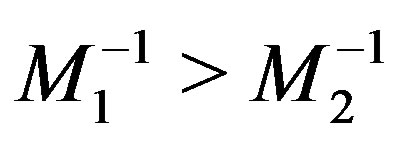 and
and  then
then

Now in the following lemma we prove that 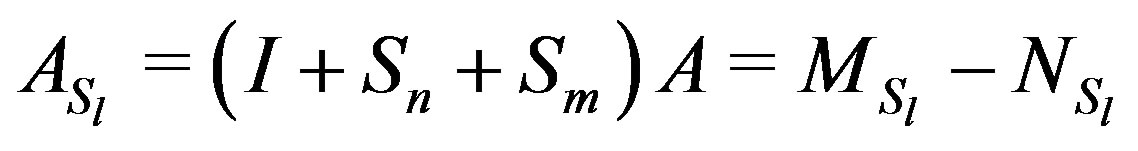 is Gauss-Seidel convergent regular splitting.
is Gauss-Seidel convergent regular splitting.
Theorem 2.12. Let A be an irreducibly diagonally dominant Z-matrix with unit diagonal, and let the condition (6) holds, then 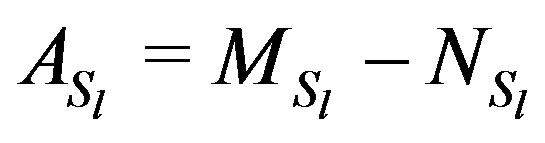 is Gauss-Seidel convergent regular splitting. Moreover
is Gauss-Seidel convergent regular splitting. Moreover
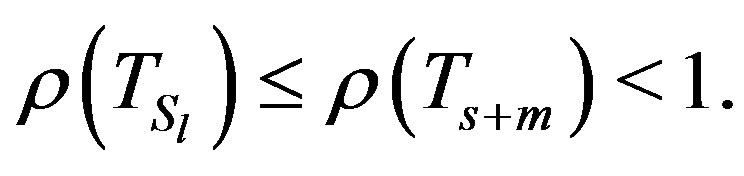
Proof. If A is an irreducibly diagonally dominant Zmatrix, then by Lemma (2.3), 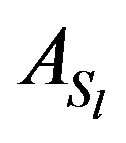 is a diagonally dominant Z -matrix. So we have
is a diagonally dominant Z -matrix. So we have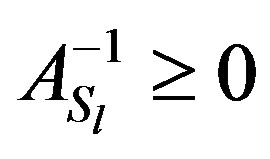 . By hypothesis we have
. By hypothesis we have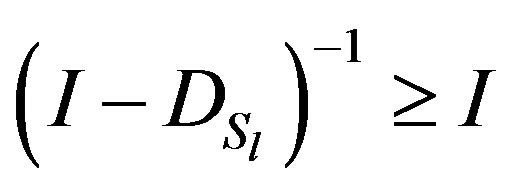 . Thus the strictly lower triangular matrix
. Thus the strictly lower triangular matrix 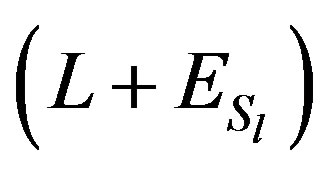 has nonnegative elements. By considering Neumanns series, the following inequality holds:
has nonnegative elements. By considering Neumanns series, the following inequality holds:

Direct calculation shows that 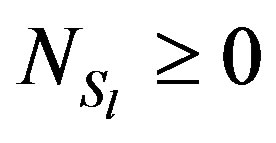 holds. Thus, by definition (2.6)
holds. Thus, by definition (2.6)  is the Gauss-Seidel convergent regular splitting. Also in [3] we have
is the Gauss-Seidel convergent regular splitting. Also in [3] we have  and
and
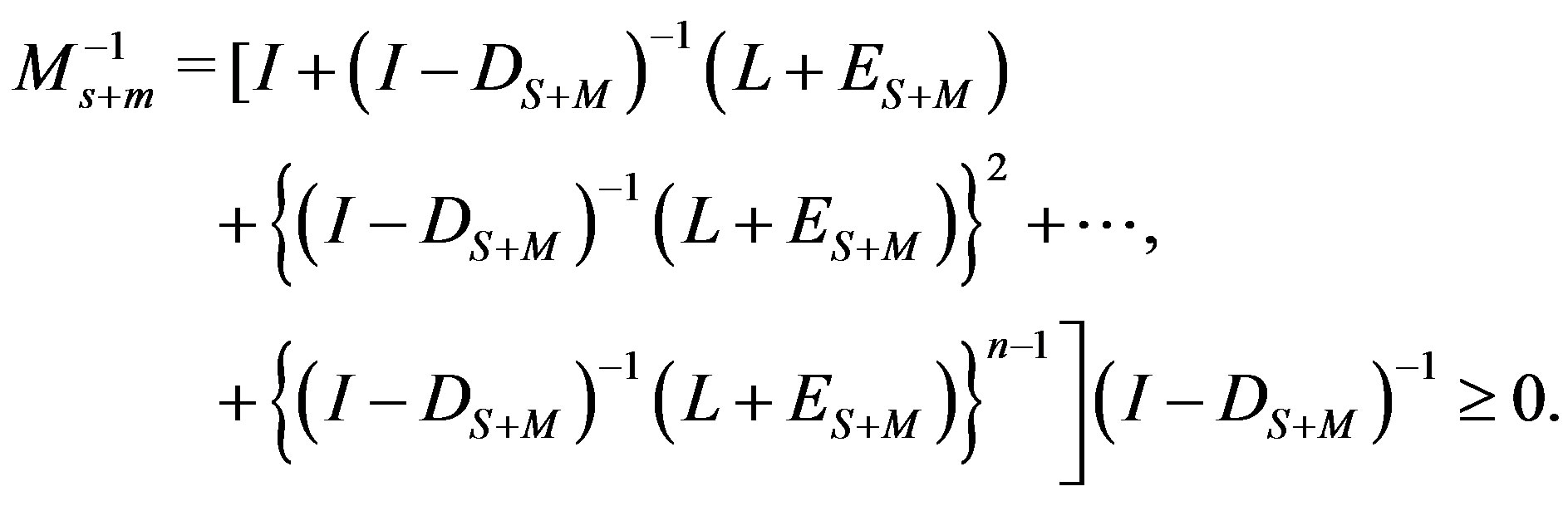
Direct comparison of the two matrix elements
 and
and 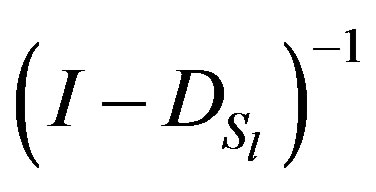 also
also  and
and
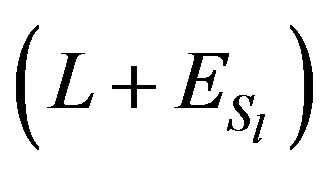 we obtain
we obtain
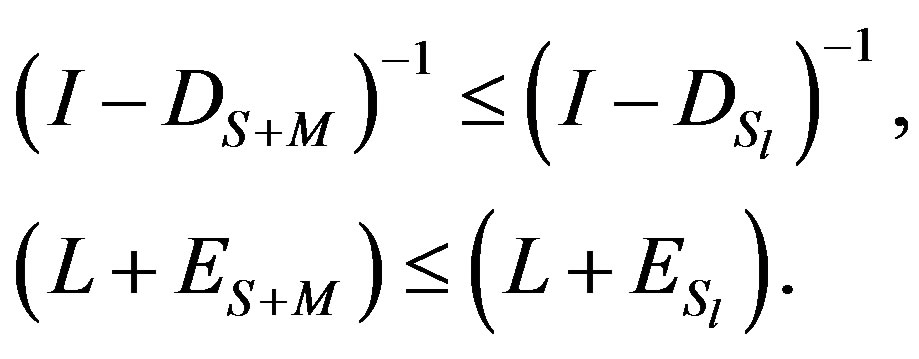
Thus
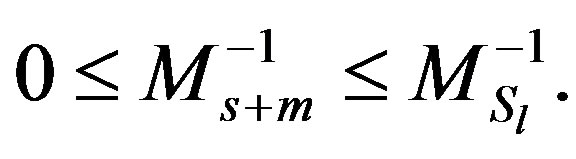
Furthermore, since , we have
, we have 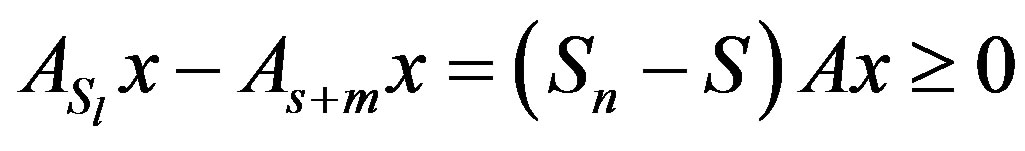 . From Lemma (2.7), x is an eigenvector of
. From Lemma (2.7), x is an eigenvector of 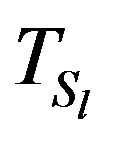 , and x is also a Perron vector of
, and x is also a Perron vector of . Therefore, from Theorem (2.11),
. Therefore, from Theorem (2.11),
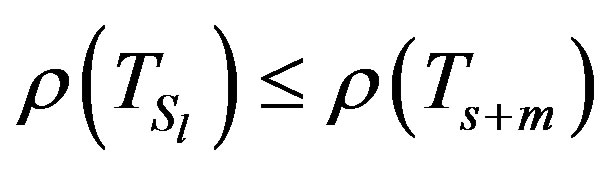
holds.
Denote

and also let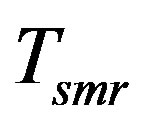 ,
,  ,
,  and
and 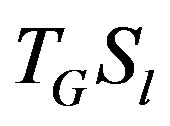 be the iterative matrix associated to
be the iterative matrix associated to ,
,  ,
, 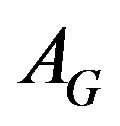 and
and 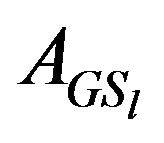 respectively. Then we can prove
respectively. Then we can prove  and
and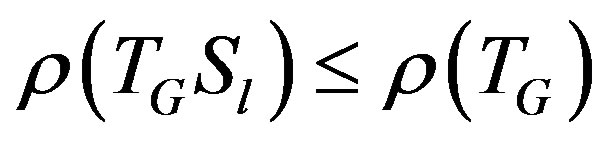 , similarly. In summary, we have the following inequalities:
, similarly. In summary, we have the following inequalities:

Remark 2.13. W. Li, in [18] used the M-matrix instead of irreducible diagonally dominant Z-matrix, therefore we can say that the Lemma 2.3 and the Theorems 2.5 and 2.12 are hold for M-matrices.
3. Numerical Results
In this section, we test a simple example to compare and contrast the characteristics of the different preconditioners. Consider the matrix

Applying the Gauss-Seidel method, we have 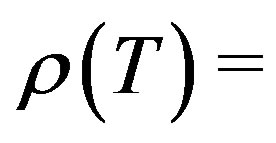
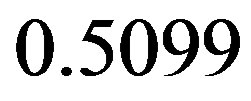 . By using preconditioner
. By using preconditioner 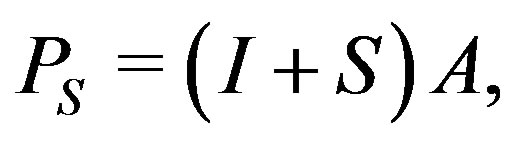 we find that
we find that 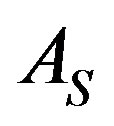 and
and 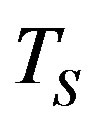 have the following forms:
have the following forms:
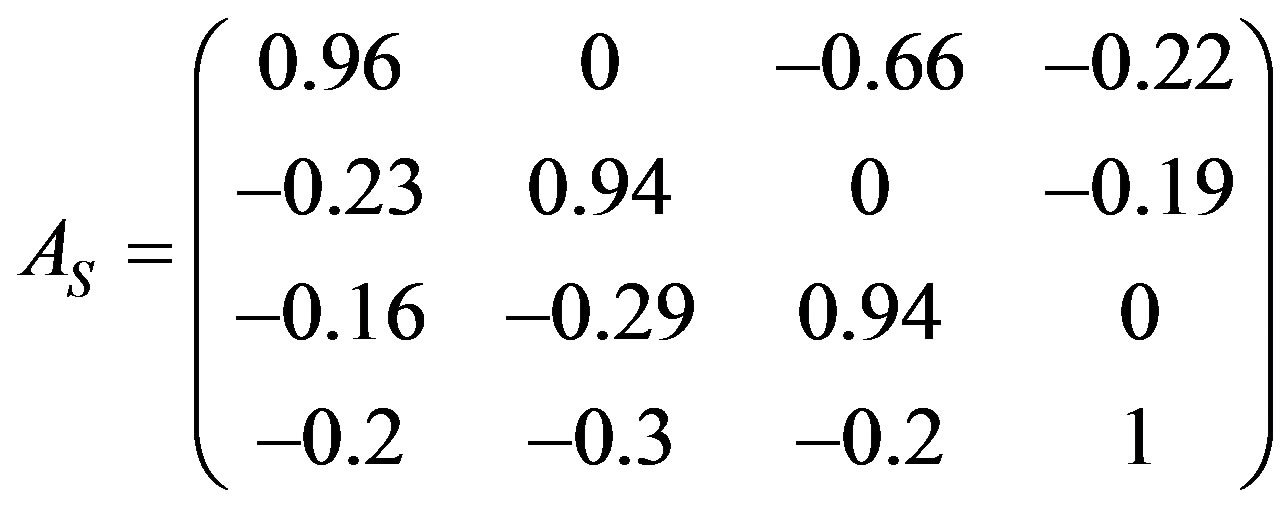

and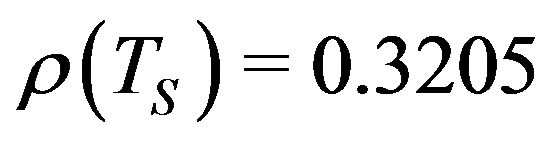 .
.
Using the preconditioner 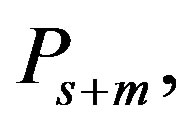 we obtain
we obtain


and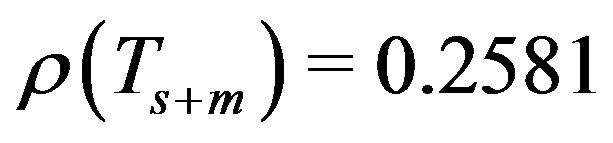 .
.
For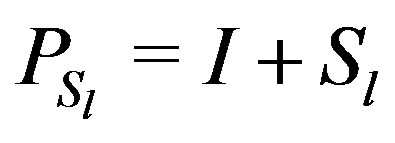 , we have
, we have


and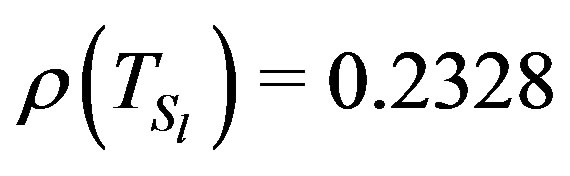 .
.
For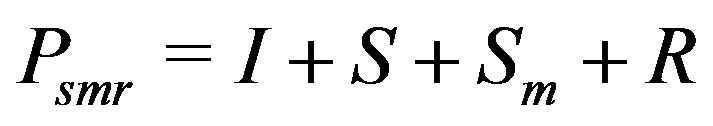 , we have
, we have


and .
.
For  we have
we have


and 
From the above results, we have 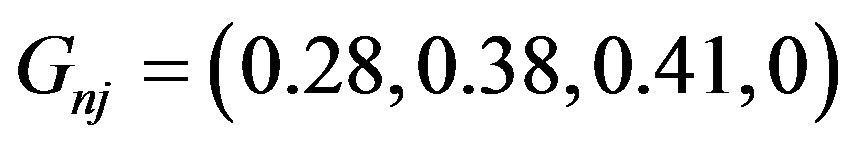 . Then
. Then  and
and  have the forms:
have the forms:

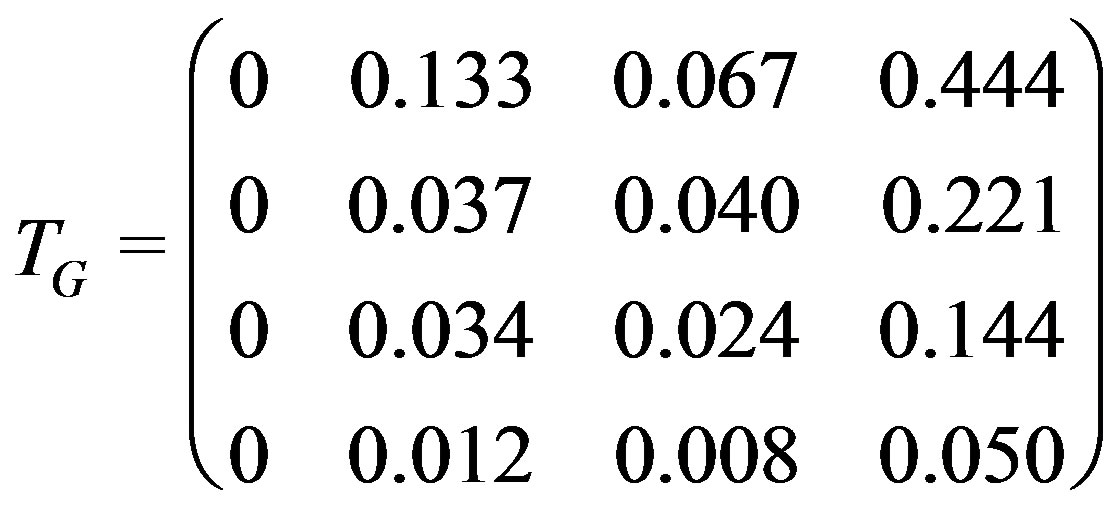
and .
.
For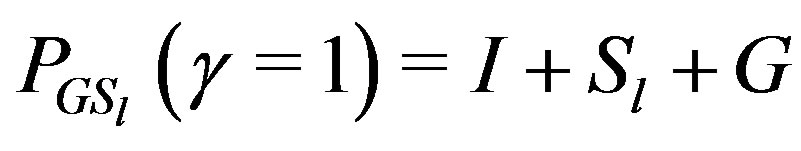 , we have
, we have


and 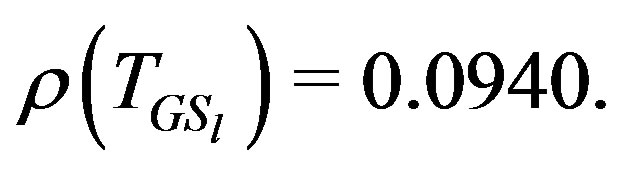 Since the preconditioned matrices differ only in the values of their last rows, the related matrices also differ only in these values, as is shown in the above results. Thus the elements of new
Since the preconditioned matrices differ only in the values of their last rows, the related matrices also differ only in these values, as is shown in the above results. Thus the elements of new  and
and 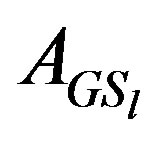 are similar to elements of
are similar to elements of 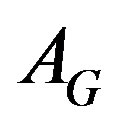 and
and , respectively than the elements of last rows. Therefore, we hereafter show only the last row.
, respectively than the elements of last rows. Therefore, we hereafter show only the last row.
By putting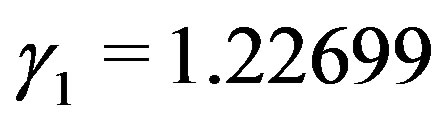 , the matrices
, the matrices 
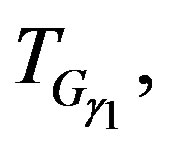
 and
and  have the following forms:
have the following forms:
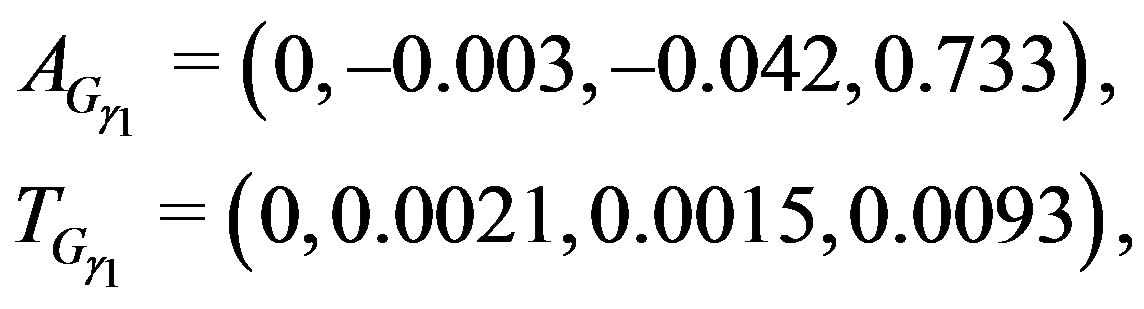
and ,
,

and .
.
For 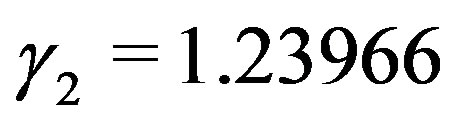 we have:
we have:

and 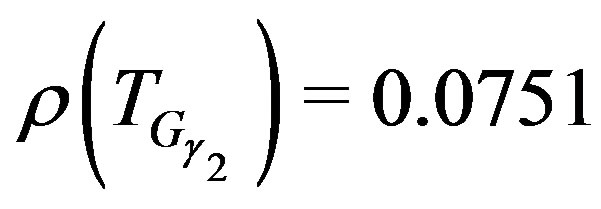 and
and
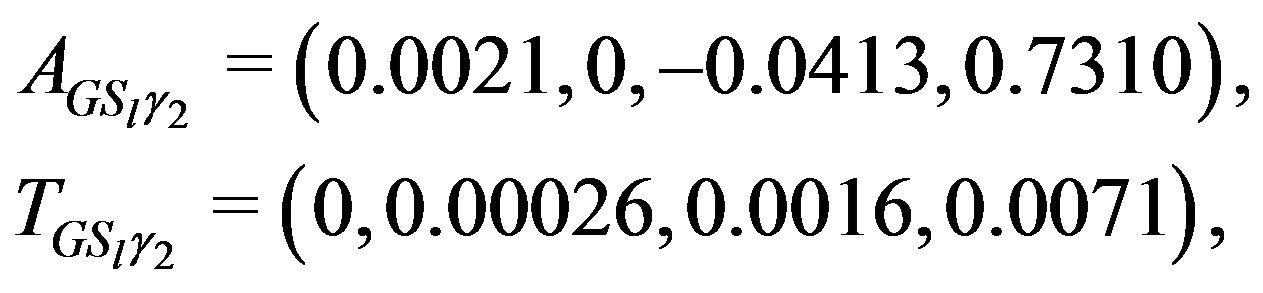
and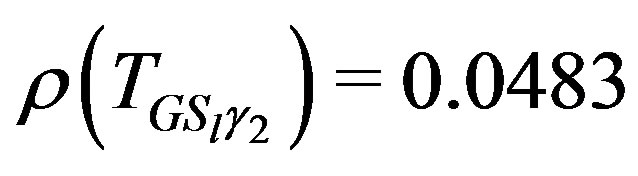 .
.
For  we have:
we have:

and 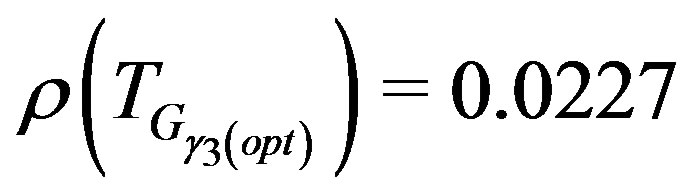 and
and
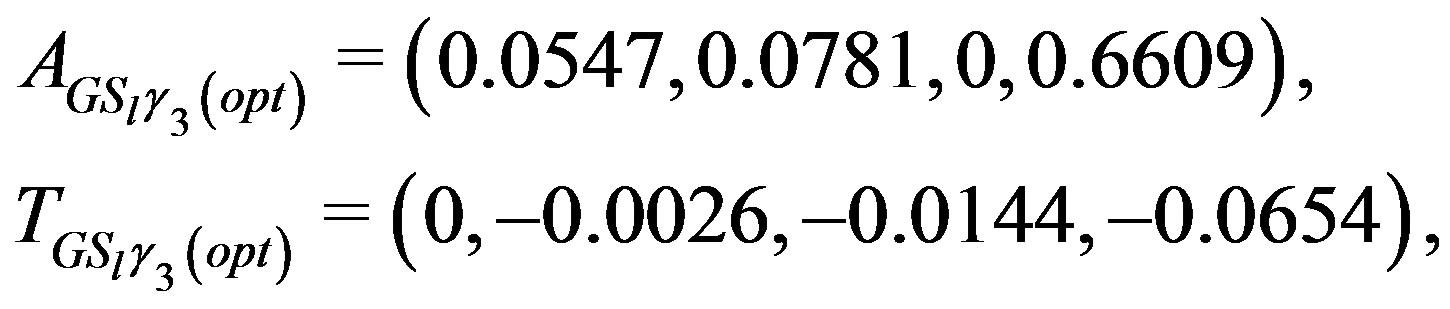
and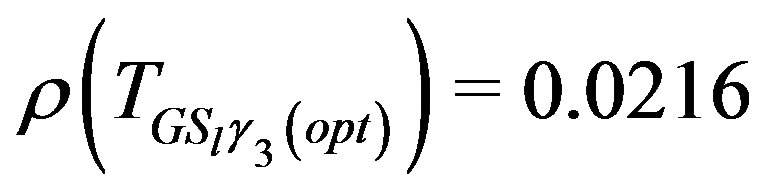 .
.
From the numerical results, we see that this method with the preconditioner  produces a spectral radius smaller than the recent preconditioners that above was introduced.
produces a spectral radius smaller than the recent preconditioners that above was introduced.
REFERENCES
- T. Z. Huang, G. H. Cheng and X. Y. Cheng, “Modified SOR-Type Ierative Method for Z-Matrices,” Applied Mathematics and Computation, Vol. 175, No. 1, 2006, pp. 258-268. doi:10.1016/j.amc.2005.07.050
- A. D. Gunawardena, S. K. Jain and L. Snyder, “Modified Iterative Method for Consistent Linear Systems,” Linear Algebra and Its Applications, Vol. 154-156, 1991, pp. 123- 143. doi:10.1016/0024-3795(91)90376-8
- M. Morimoto, K. Harada, M. Sakakihara and H. Sawami, “The Gauss-Seidel Iterative Method with the Preconditioning Matrix (I + S + Sm),” Japan Journal of Industrial and Applied Mathematics, Vol. 21, No. 1, 2004, pp. 25- 34. doi:10.1007/BF03167430
- D. Noutsos and M. Tzoumas, “On Optimal Improvements of Classical Iterative Schemes for Z-Matrices,” Journal of Computational and Applied Mathematics, Vol. 188, No. 1, 2006, pp. 89-106. doi:10.1016/j.cam.2005.03.057
- H. Niki, T. Kohno and M. Morimoto, “The Preconditioned Gauss-Seidel Method Faster than the SOR Method,” Journal of Computational and Applied Mathematics, Vol. 218, No. 1, 2008, pp. 59-71. doi:10.1016/j.cam.2007.07.002
- H. Niki, T. Kohno and K. Abe, “An Extended GS Method for Dense Linear System,” Journal of Computational and Applied Mathematics, Vol. 231, No. 1, 2009, pp. 177-186. doi:10.1016/j.cam.2009.02.005
- M. Morimoto, H. Kotakemori, T. Kohno and H. Niki, “The Gauss-Seidel Method with Preconditioner (I + R),” Transactions of the Japan Society for Industrial and Applied Mathematics, Vol. 13, 2003, pp. 439-445.
- H. Kotakemori, K. Harada, M. Morimoto and H. Niki, “A Comparison Theorem for the Iterative Method with the Preconditioner (I + Smax),” Journal of Computational and Applied Mathematics, Vol. 145, No. 2, 2002, pp. 373-378. doi:10.1016/S0377-0427(01)00588-X
- A. Hadjidimos, D. Noutsos amd M. Tzoumas, “More on Modifications and Improvements of Classical Iterative Schemes for Z-Matrices,” Linear Algebra and Its Applications, Vol. 364, 2003, pp. 253-279. doi:10.1016/S0024-3795(02)00570-0
- T. Kohno, H. Kotakemori, H. Niki and M. Usui, “Improving the Gauss-Seidel Method for Z-Matrices,” Linear Algebra and Its Applications, Vol. 267, No. 1-3, 1997, pp. 113-123.
- W. Li and W. Sun, “Modified Gauss-Seidel Type Methods and Jacobi Type Methods for Z-Matrices,” Linear Algebra and Its Applications, Vol. 317, 2000, pp. 227-240. doi:10.1016/S0024-3795(00)00140-3
- J. P. Milaszewicz, “On Modified Jacobi Linear Operators,” Linear Algebra and Its Applications, Vol. 51, 1983, pp. 127-136. doi:10.1016/0024-3795(83)90153-2
- J. P. Milaszewicz, “Improving Jacobi and Gauss-Seidel Iterations,” Linear Algebra and Its Applications, Vol. 93, 1987, pp. 161-170. doi:10.1016/S0024-3795(87)90321-1
- H. Niki, K. Harada, M. Morimoto and M. Sakakihara, “The Survey of Preconditioners Used for Accelerating the Rate of Convergence in the Gauss-Seidel Method,” Journal of Computational and Applied Mathematics, Vol. 164- 165, 2004, pp. 587-600. doi:10.1016/j.cam.2003.11.012
- D. M. Young, “Iterative Solution of Large Linear Systems,” Academic Press, New York, 1971.
- R. S. Varga, “Matrix Iterative Analysis,” Prentice-Hall, Englewood Cliffs, 1962.
- I. Marek and D. Szyld, “Comparison Theorems for Weak Splittings of Bound Operators,” Numerische Mathematik, Vol. 58, No. 1, 1990, pp. 387-397. doi:10.1007/BF01385632
- W. Li, “Comparison Results for Solving Preconditioned Linear Systems,” Journal of Computational and Applied Mathematics, Vol. 176, No. 2, 2005, pp. 319-329. doi:10.1016/j.cam.2004.07.022

