Computational Molecular Bioscience
Vol.4 No.1(2014), Article ID:43792,3 pages DOI:10.4236/cmb.2014.41002
Use of Quantum Trajectories in Computational Molecular Bioscience
Burke Ritchie
Lawrence Livermore National Laboratory, Livermore Software Technology Corporation, Livermore, USA
Email: ritchie@lstc.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 7 February 2014; revised 28 February 2014; accepted 7 March 2014
ABSTRACT
A spin-dependent quantum trajectory methodology is outlined which achieves electron exchangecorrelation on an ab initio basis. The methodology is intended to give workers in electronic structure the same computational capability which has been available for decades in classical dynamics.
Keywords:Quantum Trajectory; Exchange-Correlation; Pauli Exclusion Principle

Should computational resources continue to be devoted to the further implementation of approximate methods of molecular electronic structure? In this brief report, I point out that a first-principles theory for electron exchange-correlation based on a quantum trajectory methodology has been available in principle since Dirac’s 1928 paper for a relativistic electron but has not been implemented until recently [1] [2] owing to the ascendancy of Schroedinger theory in the intervening years. This neglect appears to originate with the canard that Schroedinger theory is valid except in the regime of high electron velocity in a high-Z regime of atomic structure. This can’t be true since electron spin is ubiquitous in the low-Z regime of electronic structure, and electron spin is a property of Dirac’s and not of Schroedinger’s equation.
The classical trajectory has a long and distinguished history in chemistry including chemical-reaction and molecular dynamics. The passage from relativistic classical to relativistic quantum dynamics simply replaces Newton’s deterministic equation of motion with Dirac’s wave equation of motion for any one electron in an ensemble,
 (1)
(1)
where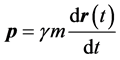 ,
,  ,
,  ,
, 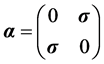 , and
, and 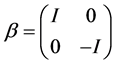 for Pauli’s spin vector
for Pauli’s spin vector
 and the 2 × 2 identity matrix I. Notice the passage from classical to quantum dynamics of Coulomb’s Law
and the 2 × 2 identity matrix I. Notice the passage from classical to quantum dynamics of Coulomb’s Law
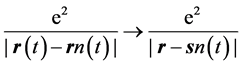 for the interaction of any two electrons whose trajectories are at
for the interaction of any two electrons whose trajectories are at 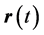 and
and
 classically and at
classically and at 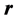 and
and 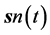 quantum mechanically. The generalization to many electrons is obvious. For example for any two electrons equations of motion analogous to Equation (1) would be written for the primed-variable electron whose interaction with the other electron would now be expressed using the unprimed variable.
quantum mechanically. The generalization to many electrons is obvious. For example for any two electrons equations of motion analogous to Equation (1) would be written for the primed-variable electron whose interaction with the other electron would now be expressed using the unprimed variable.
The quantum trajectory is calculated for the unprimed-variable electron as follows. First this electron’s velocity field 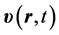 is inferred from its current,
is inferred from its current,
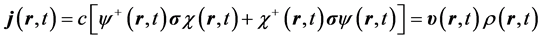 , (2)
, (2)
where  and from which a trajectory,
and from which a trajectory, 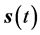 , can be calculated from the time integration of the velocity field to find a position field,
, can be calculated from the time integration of the velocity field to find a position field,
 , (3)
, (3)
and finally by finding the quantum expectation value of the position field,
 (4)
(4)
and similarly for the primed electron.
In the nonrelativistic regime of electron velocity the current is evaluated in the nonrelativistic limit using
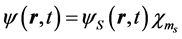
and

where  and
and 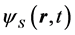 obeys the time-dependent Schroedinger equation,
obeys the time-dependent Schroedinger equation,
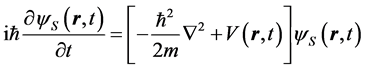 . (5)
. (5)
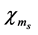 has up (plus sign) or down (minus sign) spin states denoted by
has up (plus sign) or down (minus sign) spin states denoted by 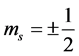 (i.e.
(i.e. 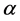 or
or 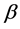 spin states)
spin states)
respectively. Written out explicitly in terms of the large component the current given by Equation (2) becomes
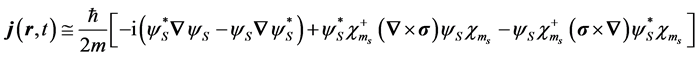 , (6)
, (6)
where we have used  and the identity,
and the identity,
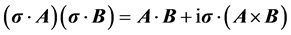
from which the identities useful in evaluating the current can be inferred,
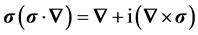 (7)
(7)
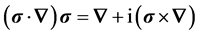 . (8)
. (8)
Written out explicitly for up (upper sign) or down (lower sign) spin states the current in the nonrelativistic regime is
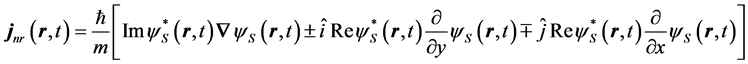 (9)
(9)
The first term on the right side of Equation (9), which is independent of spin, is contributed by Schroedinger theory, while the second and third terms are contributed uniquely by Dirac theory. Notice that the current and therefore a quantum trajectory scale like all of the other Schroedinger contributions, namely as 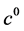 and not as
and not as , whose terms have been dropped in the Schroedinger limit of Dirac’s equation. It is found in [1] [2] that Pauli’s exclusion principle is satisfied automatically on using the spin-dependent quantum trajectories given by Equation (9) to calculate the electron-electron Coulomb potential. Hence one may conclude that electron exchange-correlation—it was recognized by the authors of early highly accurate variational calculations [3] that exchange is automatically satisfied when correlation is calculated exactly—and Pauli-Dirac statistics are relativistic effects which persist into the nonrelativistic regime. This is obvious on recognizing that spin is a property of a relativistic electron such that in Schroedinger theory the Pauli principle must be satisfied on an ad hoc basis from phenomenological observation requiring great mathematical labor to simulate the physical link between electron spin and electron correlation which is omitted in Schroedinger’s formulation of quantum theory.
, whose terms have been dropped in the Schroedinger limit of Dirac’s equation. It is found in [1] [2] that Pauli’s exclusion principle is satisfied automatically on using the spin-dependent quantum trajectories given by Equation (9) to calculate the electron-electron Coulomb potential. Hence one may conclude that electron exchange-correlation—it was recognized by the authors of early highly accurate variational calculations [3] that exchange is automatically satisfied when correlation is calculated exactly—and Pauli-Dirac statistics are relativistic effects which persist into the nonrelativistic regime. This is obvious on recognizing that spin is a property of a relativistic electron such that in Schroedinger theory the Pauli principle must be satisfied on an ad hoc basis from phenomenological observation requiring great mathematical labor to simulate the physical link between electron spin and electron correlation which is omitted in Schroedinger’s formulation of quantum theory.
Notice finally that a first-principles understanding of Fermi-Dirac statistics makes available to us a new highly practical computational methodology in which one needs an efficient, accurate solver for the 3D time-dependent Schroedinger equation and an efficient, accurate, energy-conserving integrator for the quantum trajectories. Configuration interaction (CI) calculations are obviated since the time-dependent solution automatically generates a superposition of ground and excited states. One should not fuss that the electron-electron Coulomb potential has a mixed evaluation using an independent position variable for one electron and a dependent position variable for the other electron: quantum mechanics allows us latitude to calculate the inverse distance between two point particles as long as it is calculated wave mechanically and not deterministically. The mathematical bête noir of conventional time-independent many-electron quantum theory is of course the electronelectron Coulomb potential expressed as an inverse distance using independent position vectors for both electrons. Quantum mechanics does not require us to seek a single wave function for N electrons instead of N wave functions for N electrons, and the former appears to be an accident of the additivity of the Schroedinger Hamiltonian leading to a vast literature on independent-electron approximation methods and on scholastic research on density functionals in which angels are replaced by orbitals. Except for the Bethe-Salpeter equation for two fermions, relativistic invariance is satisfied by a one-body Dirac equation in 4-space: three spatial variables and the scaled time ct. Hence in Dirac theory it is natural to write N wave functions for N fermions as in Equation (1) instead of one wave function for N fermions. As long as the electron-electron potential is written as an exact instantaneous interaction in 3-space and the time, then both electron exchange-correlation and its corollary FermiDirac statistics will be dynamically achieved.
References
- Ritchie, B. (2011) Quantum Molecular Dynamics. International Journal of Quantum Chemistry, 111, 1-7. http://dx.doi.org/10.1002/qua.22371
- Ritchie, B. and Weatherford, C.A. (2013) Quantum-Dynamical Theory of Electron Exchange Correlation. Advances in Physical Chemistry, 2013, 497267.
- James, H.M. and Coolidge, A.S. (1933) The Ground State of the Hydrogen Molecule. The Journal of Chemical Physics, 1, 835. http://dx.doi.org/10.1063/1.1749252

